弓形截面柱状相变储热装置热性能数值模拟

2022-03-25韩中合王晓帅

热力发电 2022年3期

韩中合，王晓帅

（华北电力大学电站能量传递转化与系统教育部重点实验室，河北保定 071000）

随着“3060目标”的提出，提升现有能源利用率和扩大可再生能源在整体能源中的占比已刻不容缓，而储能技术在其中扮演重要角色。其中，相变储热技术因具有高储能容量、几乎恒定的换热温差等特点而表现出高效性[1]和可跨时性，被广泛应用于太阳能发电、空调制冷制热、建筑储热材料、农业养殖等领域[2-5]。但相变材料（phase change material，PCM）热导率较低，传统储热装置结构不合理使得储/放热时间较长，不利于快速响应。

几十年来，研究人员在提升相变储热装置热性能方面进行了大量研究，这些研究大多集中于增加传热面积和改变传热流体运行工况等方面。Mahdi等人[6]对三联管相变储热装置上部和下部加装不同尺寸纵向翅片的储热过程进行了数值研究，发现在内管的上半部分添加少量中型翅片即可大幅提高PCM的熔化速率。Sciacovelli等人[7]研究了在圆管型相变储热装置中添加树形肋片对装置性能的影响，发现在使用具有2个分叉的翅片时，放热效率提升了约24%。王君雷等[8]通过数值模拟研究了储热管内翅片形式对储热性能的影响，发现螺旋翅片可以增大换热面积，减少12.21%的熔化时间。Mahdi等人[9]通过对3层同心圆管排列组成的储热系统进行数值模拟，发现该结构可以显著提高储热效率。此外，通过提高传热流体参数，如入口温度、流速等，也可增大换热系数，进而提升储热效率[10-13]。

近年来，通过加强装置内材料在熔化时发生的对流换热来提升PCM熔化速率的研究也引起了重视。Mao等人[14]通过对比圆台型和传统圆柱型储热系统，发现圆台型设计具有较高的储热效率，相同条件下，储热时间比传统模型减少30.69%。Cao等人[15]通过对偏心卧式储热装置的储热过程进行实验和数值模拟，发现偏心管设计可以有效利用材料熔化时的对流传热来提升储热速率，但Yusuf等人[16]提出偏心装置会降低PCM的凝固速率，使材料凝固时间有一定延长。

以上研究中：添加肋片会增加装置制造工艺复杂性；使用多层套管模型会大幅提升装置成本；增加传热流体流速会增加泵功，且影响系统运转；偏心管式设计可以避免上述问题，但会增加凝固时间。基于此，本文提出一种弓形截面柱状相变储热模型，并对其储热和放热过程进行了数值模拟，发现该装置可大幅提升储热效率，并对凝固时间几乎无影响。此外，该模型制作不涉及添加肋片等复杂方法，制造工艺简单，成本低，具有较好的储热特性和较高的经济性。研究结果可为研究高效储热装置的设计提供参考。

1 模型建立

1.1 几何模型和边界条件

因本文主要针对储热装置截面处PCM的熔化和凝固情况进行模拟，且Agyenime等人[17]的实验结果显示，对于轴向的温度梯度，单元内本质上存在二维传热，故可将储热单元简化为二维计算模型，内管的边界条件认为是等温的。传统卧式圆柱形相变储热模型如图1a)所示。内管中以水作为换热流体，内、外管之间的环形区域填充有相变储热材料月桂酸（LA），其相关物性见表1[18]。外管半径Ra=40 mm，内管半径Rb=20 mm。内、外管材质为钢，外管壁外包裹有保温材料。

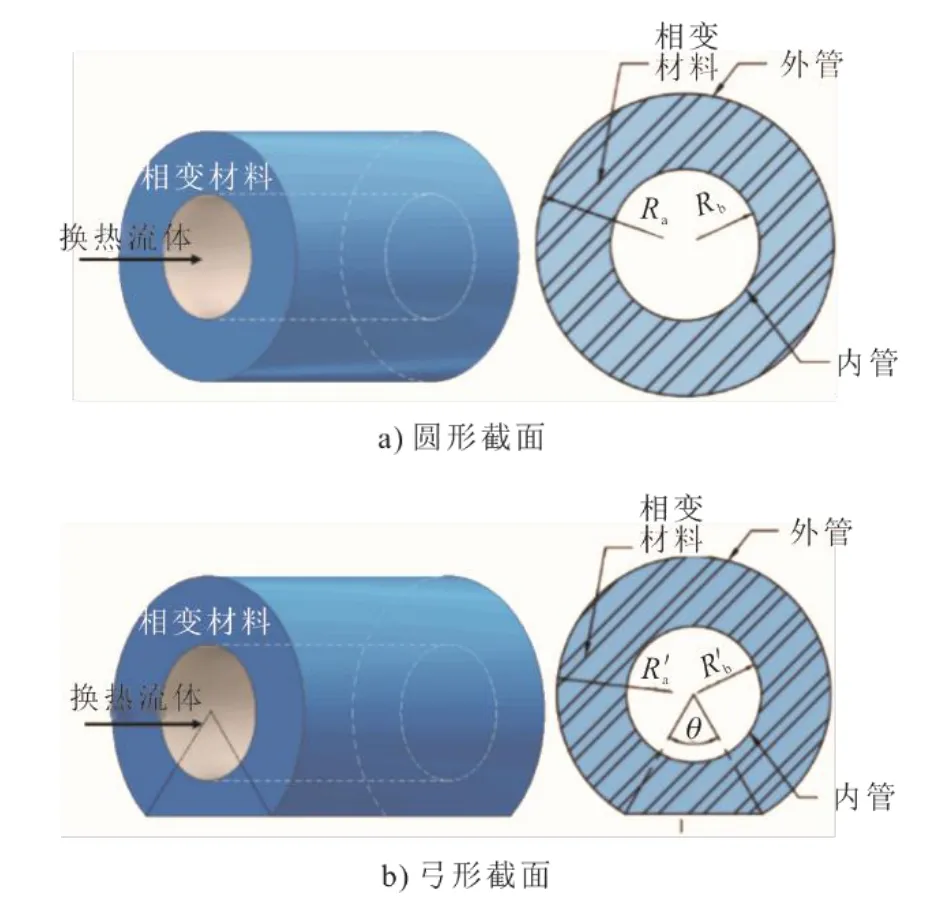
图1 圆形截面和弓形截面柱状相变储热单元示意 Fig.1 Schematic diagram of horizontal cylindrical phase change heat storage unit with circular section and bow section

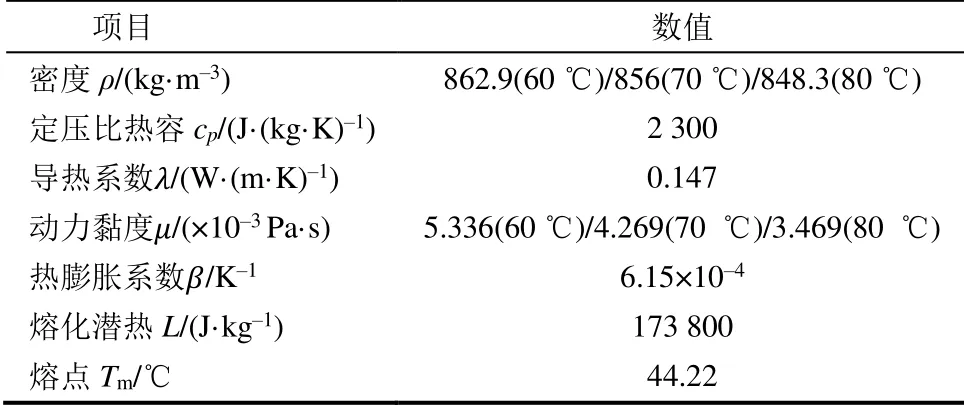
表1 月桂酸的相关物性 Tab.1 Thermophysical properties of Lauric acid

分析PCM在传统圆形截面模型的熔化过程发现，在内、管外上半区域，PCM因对流换热作用快速熔化，但在熔化末期圆管底部的少量PCM需很长时间才能完全熔化。结合以上特点，为增大换热内管外上部区域面积，减少底部PCM材料熔化时间，本文设计出一种弓形截面水平管壳式相变储热装置。该装置模型由圆柱形相变储热装置改进而来，主要结构与传统模型一致，内管流动有传热流体，外管和内管之间的环形区域填充有PCM，但弓形截面管壳式储热单元外管截面形状为弓形，物理模型如图1b)所示。

弓形截面管壳式储热单元与圆柱形储热单元的主要区别在于其底部为平面。为保证储热量不变，在其他情况相同的条件下，可视为截面积不变，此时内管管径保持不变，外管管径为：

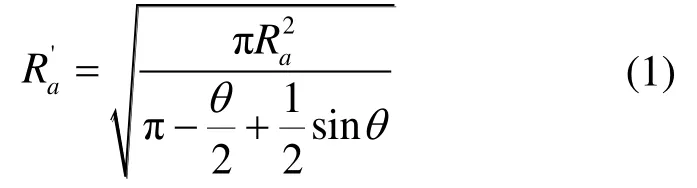
1.2 数学模型与求解方法

采用焓-多孔介质模型和有限元体积法，为方便计算，进行以下假设：

1）熔化后的液体视为不可压缩流体；

2）外部圆管为绝热壁面；

3）在计算时使用Boussinesq假设，只考虑由温差引起的浮升力项时才考虑密度的变化。

基于此，在全部PCM所在区域建立统一的能量方程，采用数值计算方法得到热焓分布，并求出固液相界面。模型的控制方程如下[19]。

连续性方程为：

式中：为速度矢量。

动量方程为：

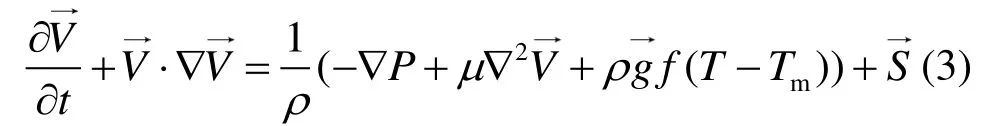
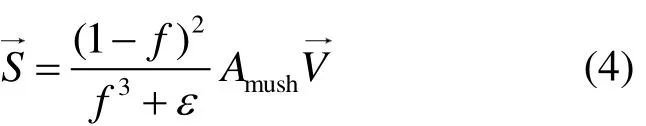
式中：f为熔化分数；Amush为糊状区因子，该参数数值一般较大，取值范围为104～107，本文取105。为了避免分母为0，在分母上添加一数值很小的常量ε=0.001[20]。

能量方程[21]为：

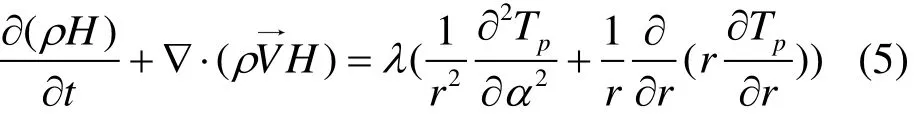
式中：Tp为相变材料温度；α为角度；r为径向长度；H为PCM焓值，J/kg，其为显热焓值h和潜热焓值ΔH之和，表达式为式(6)。

其中：

式中：L为熔化潜热。当f从0到1变化时，ΔH相应地由0变化到L，f表达式见式(8)。

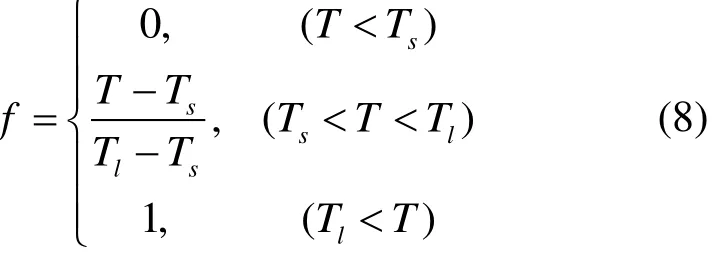
为求解控制方程，相变单元内边界条件设置为：

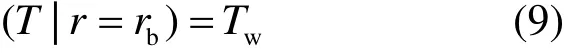
式中：Tw为加热面温度；r为距圆心点的距离；rb为内管半径。

相变单元外边界条件设置为：

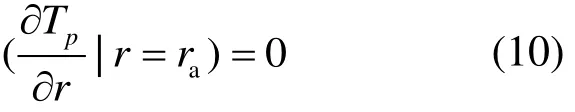
式中：ra为外管半径。

数值求解采用Fluent软件，选择基于焓-多孔介质模型的solidification & melting模型，采用PRESTO校正压力，压力速度耦合使用SIMPLE算法，能量和动量方程使用二阶迎风格式进行离散，压力、密度、动量、能量和液体分数的亚松弛因子分别为0.3、1、0.7、1和0.9。模型的网格无关性验证和时间步长验证结果如图2、图3所示。

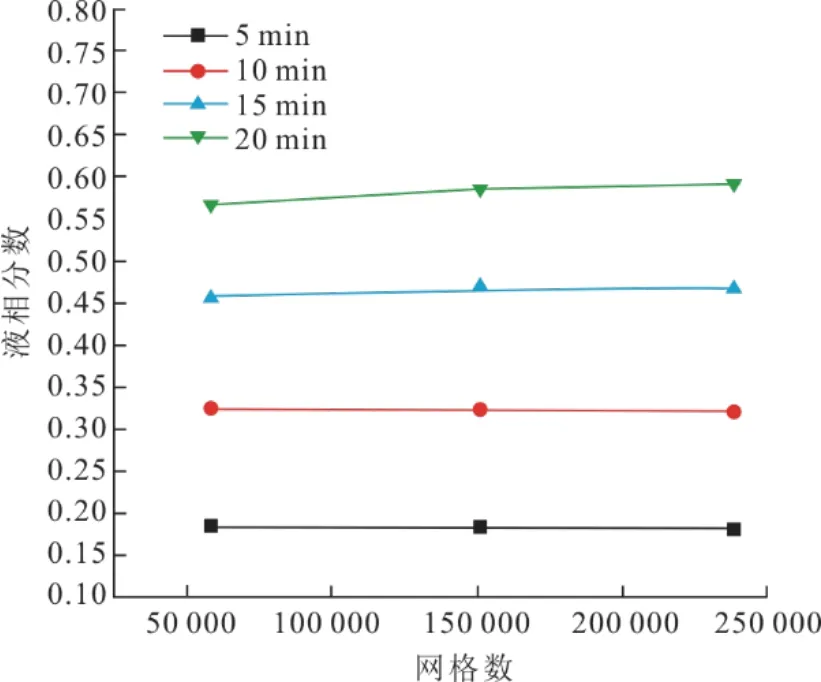
图2 网格无关性验证结果 Fig.2 The grid independence verification result

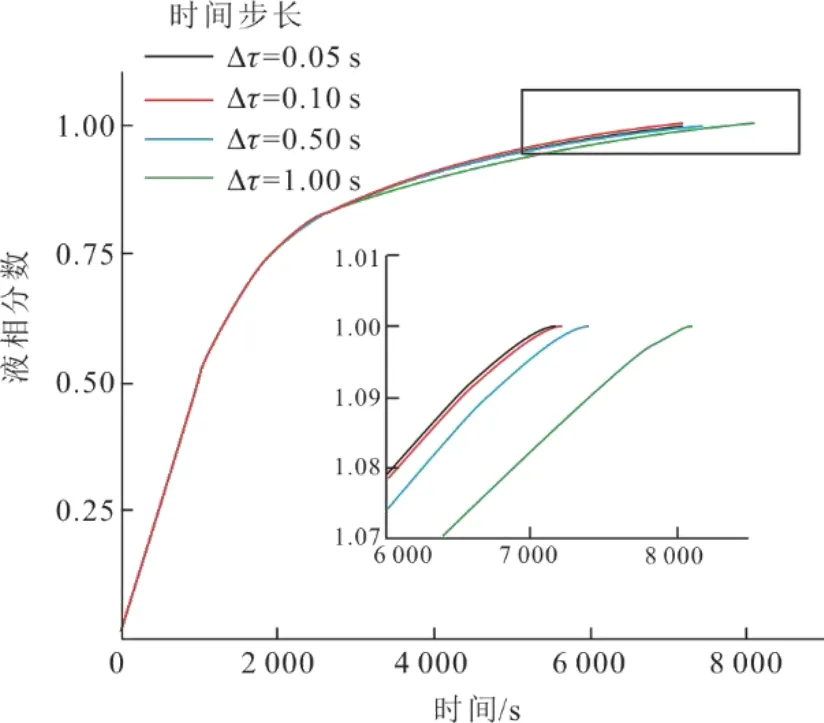
图3 时间步长验证结果 Fig.3 The time step verification result

通过独立性验证试算得出，网格数为151 200、步长设定为0.1 s既可以保证计算准确性也能兼顾计算时长，每个时间步长的迭代次数设定为20次。

2 模型验证

为验证本文数值计算方法，将本文建立的圆形截面模型模拟结果与文献[22]中的实验和模拟结果进行了对比，PCM液相分数随傅里叶数Fo的变化曲线如图4所示。其中，储热实验内管温度为80 ℃，相变储热材料为月桂酸。

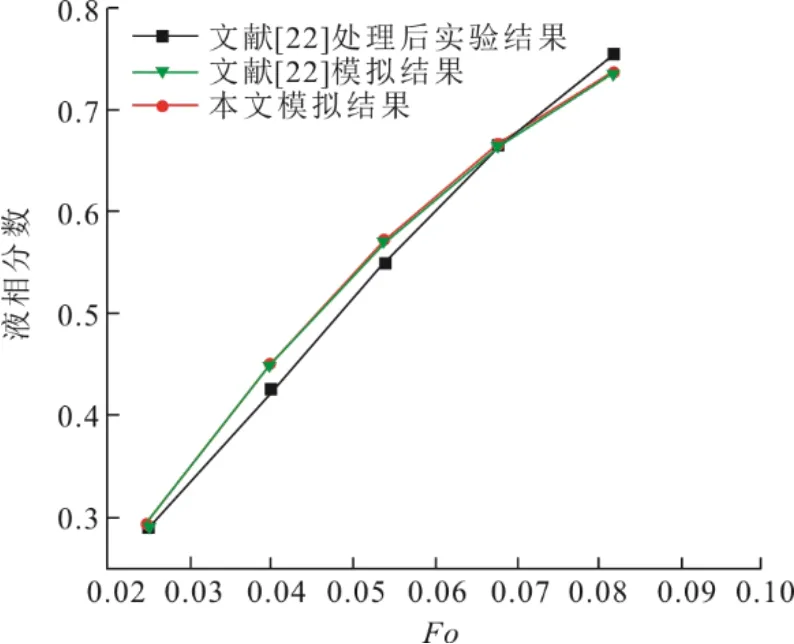
图4 本文模拟结果与文献[22]数据对比 Fig.4 Comparison between the simulation results in this paper and the data obtained in literature [22]

3 结果与分析

3.1 PCM熔化和凝固传热特性

对换热管直径为40 mm、外管直径为80 mm的传统圆形截面储热单元以及内径为40 mm、截面积与前者相同的弓形截面储热单元的储热和放热过程进行数值模拟。储热过程选择内管温度为60、70、80 ℃，PCM为25 ℃时进行模拟计算，凝固过程选择在冷却温度为25 ℃，PCM为60、70、80 ℃时进行模拟计算。分析储热过程时取加热温度为80 ℃的情况作为代表，两者储热过程中PCM的液相分数变化曲线、固/液相界面变化、温度云图和流线图如图5—图7所示。

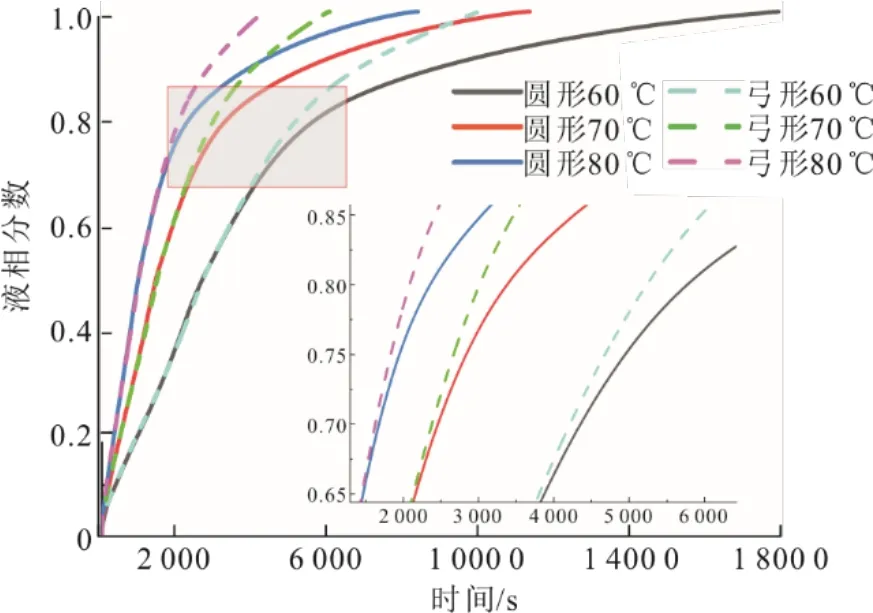
图5 圆形截面与弓形截面储热单元储热过程PCM液相分数变化曲线 Fig.5 The liquid fraction of PCM in heat storage unit with circular section and bow section in heat storage process

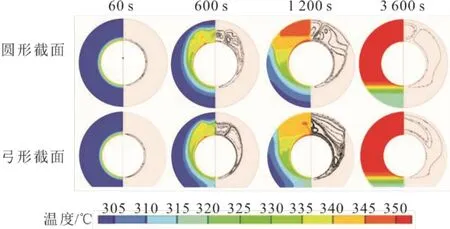
图7 加热温度80 ℃时圆形截面与弓形截面储热单元内温度云图和流线图 Fig.7 The temperature nephogram and streamline diagram in heat storage unit of the two models during heat storage at 80 ℃

对比熔化过程液相区轮廓和熔化速度可以发现，熔化过程大致可分为4个阶段：熔化初始期，熔化速率较快；熔化前期，熔化速率相较于初始期较小，但仍明显高于后一阶段；熔化中期，熔化速率一般；熔化后期，熔化速率最慢。

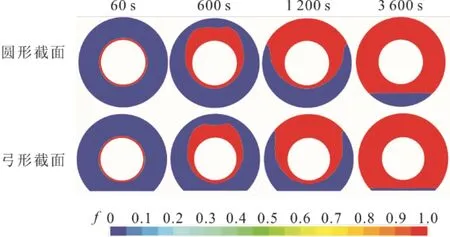
图6 加热温度80 ℃时圆形截面与弓形截面储热单元储热过程固、液相界面变化对比 Fig.6 The change of solid-liquid interface of circular section and bow section model during heat storage at 80 ℃

熔化初始期以导热为主，熔化速率较快，此时液体的量较小，流动也不明显，只是会出现微型漩涡，对熔化过程造成的影响并不明显。圆形截面与弓形截面模型中PCM熔化速率和熔化所形成的相界面一致，均为垂直于圆管呈环形向外扩展，固、液相界面近似圆环形。2种模型在该阶段各方面几乎一致。

随后的熔化前期中，2种模型的熔化速率也基本一致。在此过程中，对流传热开始起作用并逐渐达到峰值，部分固体变为液体，热量在液体中传递不均匀，导致液体温度分布不均，不同区域的液体开始产生密度差，随之产生的浮升力驱动液体流动，形成自然对流。随着液体的增多，自然对流强度和复杂性增加。部分温度较高的液体由底部上移，流动至顶部，加热顶部区域的固体PCM，顶部部分固体材料熔化后的温度较低的液体沿着固、液相界面开始向下流动，此时PCM的流动在液态区域形成规模较大的漩涡。自然对流对各区域带来的影响也不尽相同，使得在之后的固、液相界面出现了上下分布不规则的形状。

在对流换热作用开始减弱时，第3阶段出现。这时在上半区域的PCM基本已经熔化，对流换热的作用开始降低，圆形截面储热单元的熔化曲线拐点明显早于弓形截面储热单元，两模型的熔化速率出现明显差别。

第4阶段主要是底部PCM熔化过程。此阶段由对流换热带来的影响几乎可以忽略，传热方式主要为导热。图5中，弓形截面储热单元的PCM的熔化曲线斜率更大，表示熔化速率更快。由图5可以看出，在相同工作条件下，弓形截面储热单元中最后15%的固体材料的熔化时间仅为圆形截面储热单元的44.43%，而整体熔化时间缩短了48.37%。

凝固过程也选择PCM为80 ℃时的放热过程为代表进行对比分析，结果如图8、图9所示。由图8可以看出，在凝固过程中，圆形截面与弓形截面储热单元固、液相截面变化及PCM液相分数曲线基本一致，两者固、液相界面从开始到凝固末期基本均保持从内壁面等距扩大的变化规律，在末期也均为顶部材料未凝固。

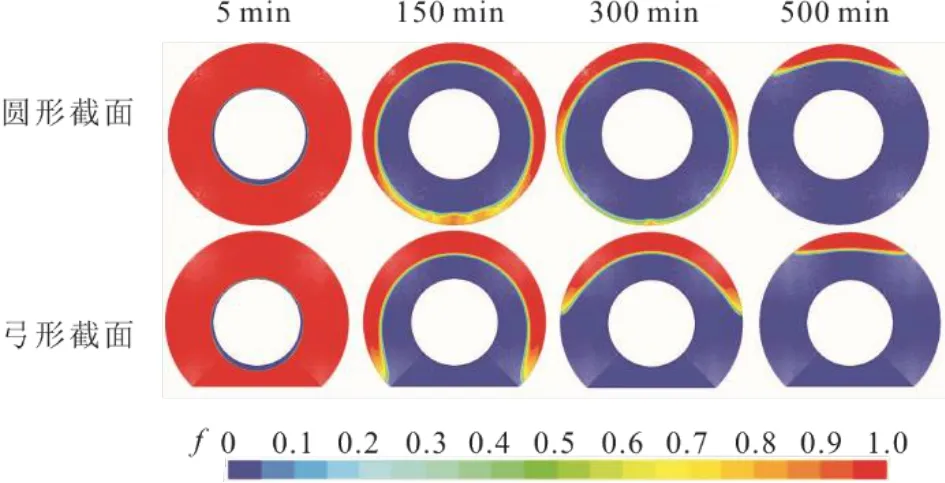
图8 初始温度80 ℃时放热过程PCM固、液相界面变化 Fig.8 The change of solid-liquid interface in exothermic process at initial temperature of 80 ℃

由图9可以看出，随着凝固过程的进行，传热热阻增大，传热速率逐渐降低，液相分数变化曲线也随之变缓，且各曲线基本重合，这主要是因为在凝固时热传导方式起主要作用，且2种截面的尺寸基本一致，各方面无明显差别。80 ℃时，弓形截面储热单元内PCM的凝固时间比圆形截面储热单元仅长0.54%。

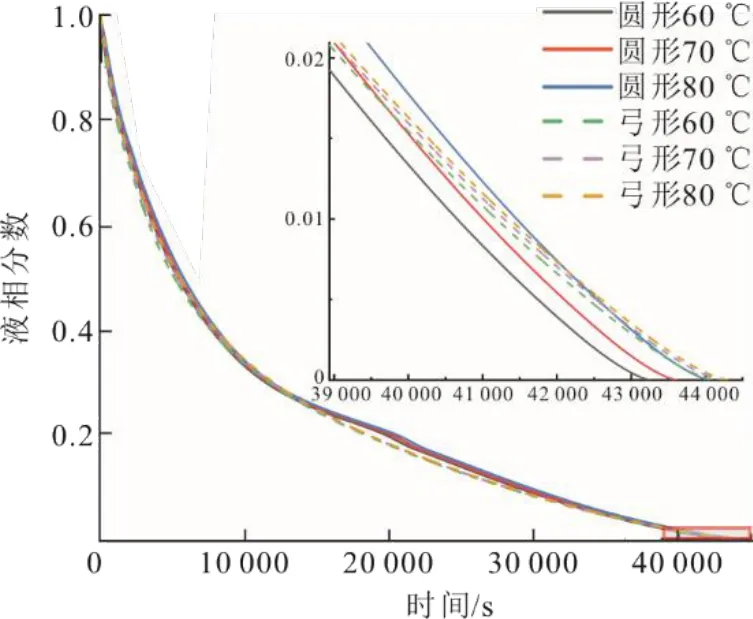
图9 放热过程PCM液相分数变化曲线 Fig.9 The liquid fractions of PCM in exothermic process

3.2 熔化和凝固传热机制

为了研究相变储热装置的传热性能，定义一定时间内的平均努塞特数为：

其中，

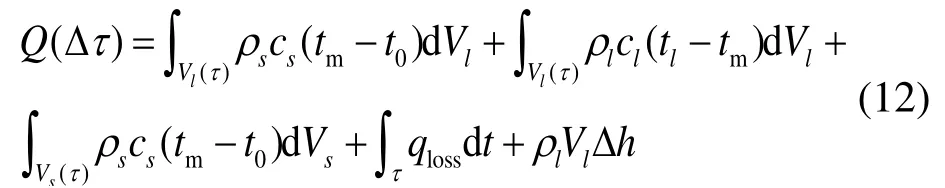
式中：A为传热面积，m2；tw为壁面温度，℃；tm为相变温度，℃；λ为导热系数，W/(m·K)；Δτ为换热时间，s，本文取30 s；Q(Δτ)为Δτ时间内的传热量，W；Vl为液相体积；Vs为固相体积；tl为液体温度；t0为初始温度；cs和cl分别为固体和液体的比热容；式(12)等式右边第4项为热损失，可以忽略不计。

由此可以得出不同阶段的以及储热过程中-Fo关系，结果如图10所示。以加热温度为80 ℃时为例，图10中A、B曲线分别为圆形截面和弓形截面模型的-Fo曲线。熔化初期时，2条曲线的均为最高，随后快速下降。这是因为刚开始主要以导热为主，此时热阻最小；随着固体熔化，液体分数增加，导热热阻快速增加，各区域温差明显，随之带来的密度差也逐渐使得自然对流形成并加剧，对流传热开始起作用，且逐渐增大并达到一峰值。随着熔化过程继续，上部液体温度分布均匀，减小，曲线逐渐平缓，在熔化末期趋于不变。

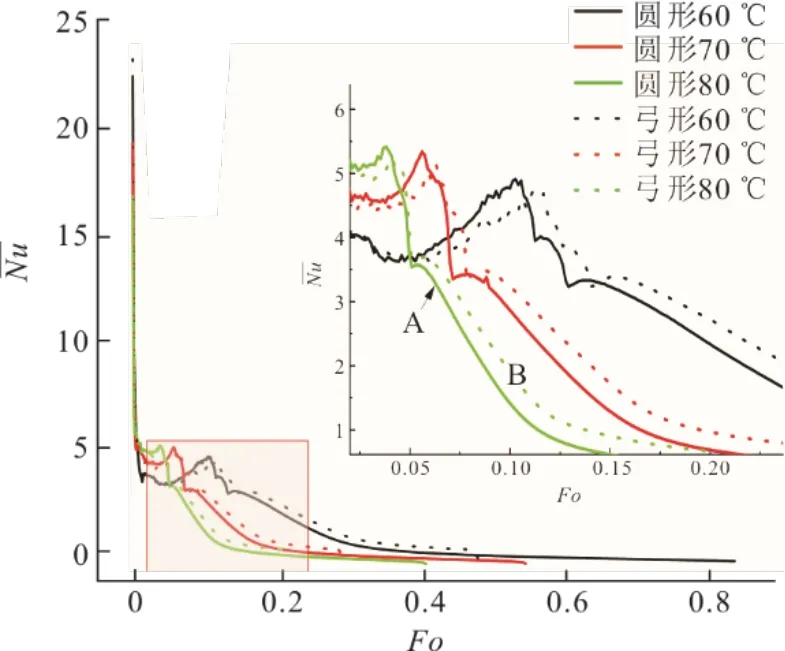
图10 储热过程各温度工况下随Fo的变化 Fig.10 Changes of with Fo in thermal storage process under different conditions

由图10可以看出，熔化初始时期A、B曲线几乎无差别，此时传热情况一致，但随后曲线A显示圆形截面模型熔化过程导热-对流转捩点在Fo为0.024左右出现，曲线B显示弓形截面模型熔化过程转捩点在Fo为0.026左右出现，且峰点出现较晚。这是因为，弓形截面使得在传热管道外部上方区域的PCM增多，有更多的PCM在对流传热的作用下熔化，从而出现B曲线自峰点后开始较晚下降的现象。在熔化末期，曲线B的持续高于曲线A，这是因为此阶段主要以热传导为主，传热速率受传热面积的影响较大，而由于弓形截面底部为平面，其底部区域PCM的固、液接触面积明显大于圆形截面，且该截面积随固体的熔化变化较小，与圆形截面传热单元相比，可有效提高换热效率，缩短换热时间。

从凝固过程来看，圆形截面和弓形截面装置对应的放热曲线的变化整体一致，固、液相界面的移动主要是沿着垂直于内管的外环方向向外近似等圆移动，表明在此过程中热量传递方式主要以热传导为主，虽然在凝固过程中也出现对流传热，但作用较弱。储热单元的外形尺寸对整个凝固过程有较大影响，但弓形截面装置的外管直径相比圆形截面增大约为4.87%，对整体带来的影响较小。

分析温度云图可知：在传统圆形截面储热单元中，上部区域的温度较高，而底部区域温度下降最快，PCM最先凝固；在弓形截面中，也是底部区域先达到凝固温度，上部区域未凝固材料距换热管道的距离及换热面积和传统圆形截面模型的基本一致，所以两者后期换热速率差别较小。这导致二者凝固过程除前期有一定差异外，整体上并无明显差别，弓形截面模型比圆形截面模型整体凝固时间长0.54%。

3.3 不同温度下PCM的熔化和凝固特性

对不同温度下PCM的熔化和凝固过程进行分析，探究不同储/放热温度对弓形截面装置热性能的影响。图10中，在不同温度下，储热过程Nu随Fo变化曲线整体趋势较为一致。但随着温度升高，因自然对流作用而出现的上升转捩点出现变早，即温度越高，对流换热起作用时间越早，且因为温度较高液体内对流运动比较剧烈，随后出现的峰值也较高，对应峰值的Fo也越小。可以认为，温度越高对流换热运动越剧烈，且随着温度的升高曲线降低得越快，证明有更多的PCM以较快的速度在以对流换热为主的换热过程中熔化。最后可以发现，相同模型不同温度下，在熔化末期温度越高也越大。随着加热温度的升高，弓形截面相变储热装置内PCM熔化时间相比传统圆形截面装置减少时间由43.85%增至48.37%，储热效率提升。

由图9可以看出：在凝固前期，凝固温差越大凝固速率越快，但是由于温度较高所以需要传递的热量较多，最终完全凝固时间也较长；由于温度提升，弓形截面模型与传统圆形截面模型中PCM的完全凝固时长之差逐渐减小。