填料双层布置对冷却塔进风预冷传热传质 过程的影响模拟研究
2022-03-25齐慧卿闫明暄庞慧敏徐梦菲何锁盈
韩 强,李 旋,齐慧卿,闫明暄,庞慧敏,张 齐,徐梦菲,何锁盈,高 明
(1.山东电力工程咨询院有限公司,山东 济南 250013; 2.山东大学能源与动力工程学院,高效节能及储能技术与装备山东省工程实验室,山东 济南 250061)
火电厂的废热通常经冷却塔排入大气[1]。我国西北地区干旱缺水,空冷塔因为节水在西北地区具有广泛的应用前景。对于空冷塔,在夏季高温时段其冷却效率极低,导致机组的循环热效率偏低,严重影响火电厂的运行经济性[2]。
研究表明[3-4],空冷塔的进风预冷可提升其在高温时段的换热性能。空冷塔的进风预冷技术主要是通过蒸发预冷塔的进风,降低进风温度的同时会导致进风湿度增大,之后被冷却后的空气与空冷塔内换热器处的热水进行间壁式换热。换热器处的换热为显热交换,过程无相变,故进风湿度增大对此处的显热交换影响不大。进风预冷一般通过喷淋和填料实现。填料蒸发预冷进风空冷塔如图1所示。在空冷塔的进风段沿着塔壳安装一圈填料(塔内部不安装填料)。水通过配水装置均匀分配到填料顶部,在重力、毛细力的作用下水均匀润湿填料;当空冷塔的进风在自然浮力的作用下流过填料时,填料上的水蒸发冷却进风,进风被冷却后进一步与塔内换热器处的热水换热,换热后将换热器处的废热排至大气;填料处未蒸发的水在填料底部收集,并在水泵作用下循环使用。
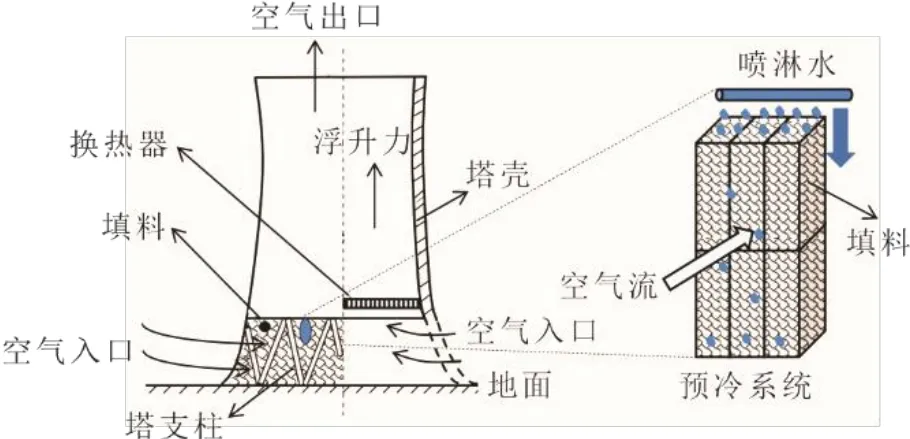
图1 填料蒸发预冷进风空冷塔[3] Fig.1 A dry cooling tower pre-cooled with wetted media[3]
填料布置方式影响空气的流动,进而影响蒸发冷却系统的性能[5-6]。Billingham等人[7]将波纹型填料进行错位排列布置,且填料之间保留一定的空隙,发现该布置形式能够使空气的最大流动通量提高30%,同时能够有效的降低空气阻力。He等人[8]研究表明,300 mm填料的冷却效率已经达到90%以上,采用400 mm填料对冷却效率的提升不大。Yan等人[9]实验研究了填料双层布置下蒸发冷却性能,实验分别对比了300 mm填料双层布置与填料常规布置在100、200、300 mm厚度下的蒸发冷却性能,研究了风速(范围为0.5~3.0 m/s)、水流量(62、31 L/(min·m2))等因素对冷却性能的影响。实验发现:填料双层布置时的冷却效率优于200 mm常规填料,压降接近于200 mm常规填料;300 mm填料双层布置与300 mm常规填料相比,其冷却效率稍低但空气侧压降较小。故对于300 mm填料双层布置,与300 mm常规填料相比,其100 mm中空可在满足冷却要求的同时减小通风阻力,且可节省100 mm填料,具有较好的经济性。基于此,本文 提出一种新的填料双层布置形式,即“100 mm填 料+100 mm中空+100 mm填料”。填料双层布置的配水系统及布置示意如图2所示。

图2 填料双层布置的配水系统及布置示意 Fig.2 The water distribution system and medium-gapmedium arrangement
本文在此基础上,利用Fluent18.0软件进一步对填料双层布置时内部的气-液传热传质过程进行深入探究,旨在揭示填料双层布置对传热传质过程的影响机制。
1 数学模型
1.1 基本假设
由于填料结构的复杂性,水和空气在填料内部流动呈紊流状态。同时,蒸发冷却过程不仅存在传热还存在传质,因此整个蒸发冷却过程较为复杂。为了简化,模拟时做如下假设:1)空气、水与外界无传热现象;2)忽略因环境变化以及传热传质引起流体物性参数的变化;3)填料全部被水湿润,且在填料表面形成一层均匀的水膜,水膜温度等于入口空气的湿球温度;4)忽略水膜厚度、流速以及表面张力;5)中空区域均匀淋水,且淋水温度等于入口空气的湿球温度;6)整个蒸发冷却过程处于稳定工况。
1.2 几何模型
本研究选取CELdek7060填料进行研究,如 图3所示。该填料是一种波纹状填料,且相邻2片填料与水平面的夹角不同,15°填料片与空气流动方向对齐,45°填料片与水流流动方向对齐。相邻2片填料通过粘合连接,其粘合处为交界面[10]。
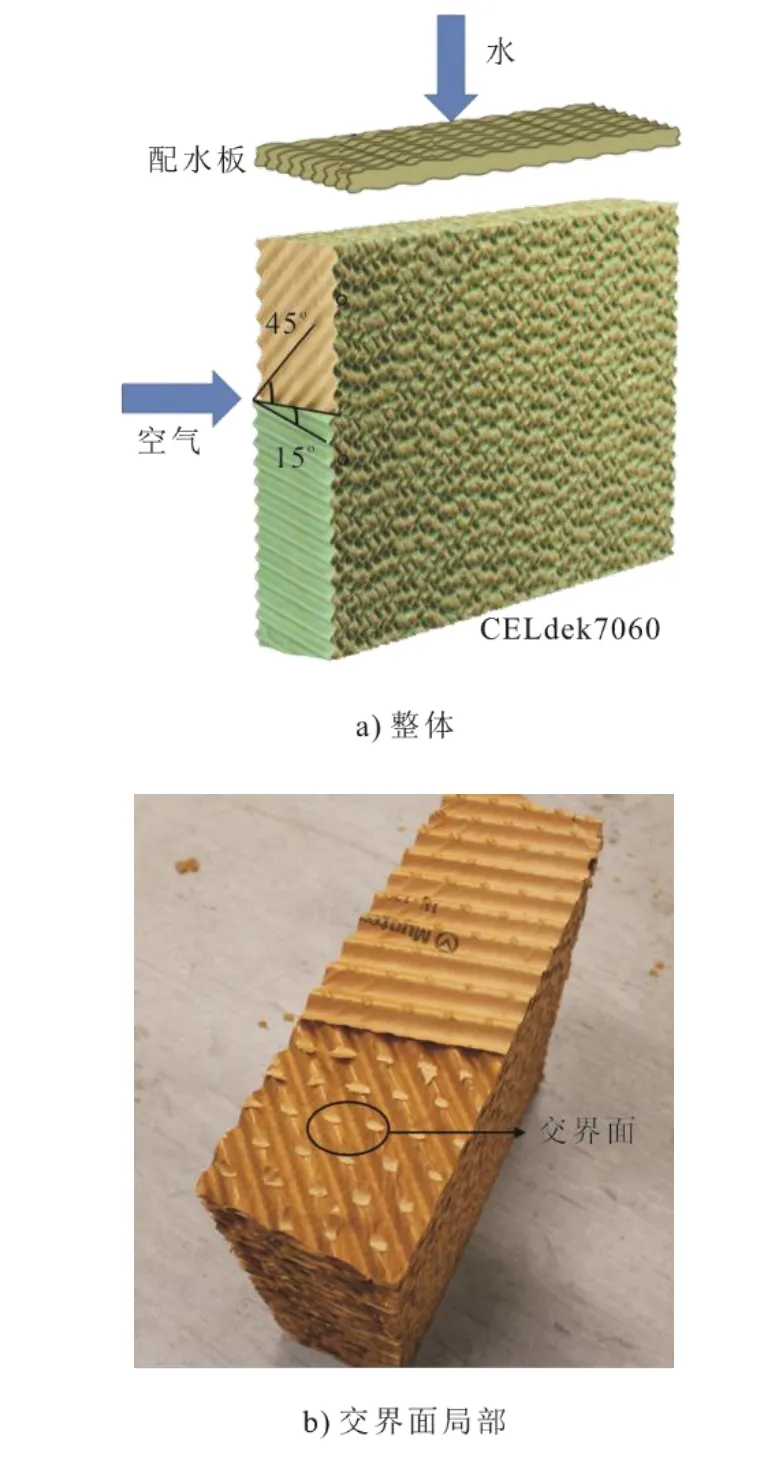
图3 CELdek7060填料的示意 Fig.3 Schematic diagram of geometric structure of CELdek7060
首先,采用Solidworks对填料双层布置结构进行建模,利用曲线拉伸功能得到填料的波纹状结构。为了节省计算时间,本文选择了4片填料组成的3个气流通道进行建模计算,模型如图4所示。模型高度200 mm,厚度300 mm(即“100 mm填料+100 mm中空+100 mm填料”)。而后,将几何模型导入到ICEM中进行网格划分。

图4 填料双层布置的三维模型 Fig.4 Three dimensional model of the medium-gap-medium arrangement
采用四面体网格对模型进行网格划分(图5),同时对网格进行独立性验证,结果见表1。

图5 网格划分 Fig.5 The mesh generation
网格独立性验证的工况为:入口空气风速为1.55 m/s,入口空气温度为300.2 K,入口空气含湿量为0.010 18,入口空气相对湿度为45.1%。空气侧温度、含湿量是衡量蒸发冷却效率的重要指标,因此将出口空气的干球温度以及含湿量作为主要的评价指标,根据表1中的网格独立性验证,选择网格数目为3 234 355进行后续计算。

表1 网格独立性验证 Tab.1 The grid independence verification result
1.3 控制方程
1.3.1 连续相控制方程
连续相为空气,是不可压缩且稳定的流体,在填料内部为湍流流动。空气的主要组分为氮气、氧气和水蒸气,研究过程中只考虑这3种物质。控制方程主要包括质量方程、动量方程、能量方程、组分守恒方程以及湍流动量和湍流耗散率方程,这些方程可以用如下的通用形式表示:
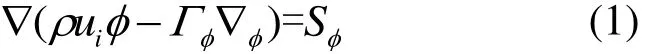
式中:ρ为空气密度,kg/m3;ui为速度矢量,m/s;Γ为广义扩散系数;Sφ为广义源项。控制方程中的广义源项为考虑水蒸发对空气作用而引入的质量、动量及能量源项。
1.3.2 离散相控制方程
对于填料区域中水膜与连续相,在填料表面会形成一层饱和空气层,该空气层与进入填料通道的未饱和空气存在着一定的温差和水蒸气分压力差。因此水膜与空气在该处会发生传热传质过程。在填料区域,利用壁面函数法对各个输运方程进行处理,从而模拟水膜与空气的传热传质过程。
对于中空区域的淋水区,水滴可以认为是离散相。通过设置水滴的温度、速度等条件来模拟液滴的运动轨迹,同时与连续相的空气进行耦合计算,从而模拟水滴与空气的传热传质过程。
水滴轨迹与速度的运动方程如下:

式中:t为时间,s;rp为水滴运动轨迹;up为水滴的瞬间速度,m/s。
水滴的温度变化如下:

式中:Tp为水滴温度,K;h为水滴和空气间的对流换热系数,W/(m2·K),计算时利用Fluent软件中内置的传热关联式对传热过程进行描述;hfg为蒸发潜热,J/kg;Ap为水滴的表面积,m2;Tadb为微元体内气相干球温度,K。水滴和空气间的对流换热系数通过式(4)计算。
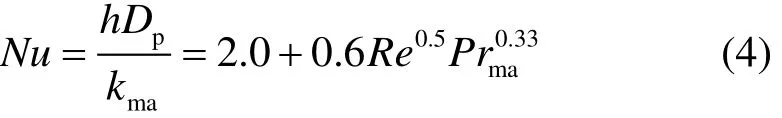
式中:Nu为努塞特数;kma为空气导热系数,W/(m·K);Prma为湿空气(连续相)的普朗特数;Re为以水滴颗粒直径为特征长度的相对雷诺数。
水滴颗粒的蒸发速率为:
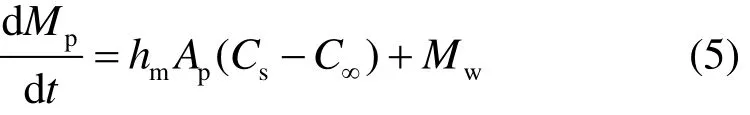
式中:hm为质量扩散系数,通过式(6)计算,kg/(m2·s),计算时利用Fluent软件中内置的传质关联式对传质过程进行描述;Mw为水滴摩尔质量,kg/mol;Cs为液滴颗粒表面水蒸气摩尔浓度,mol/L;C∞为空气中水蒸气摩尔浓度,mol/L。
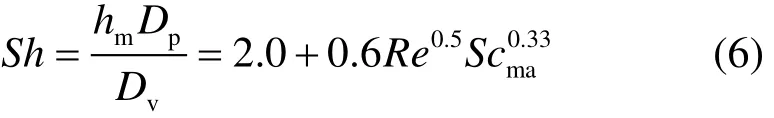
式中:Sh为舍伍德准则数;Scma为施密特准则数。
1.3.3 连续相与离散相的耦合
在中空区域,空气与水滴的换热计算通过连续相与离散相的耦合实现。当水滴通过每个微元体时,其与连续相发生质量、热量和动量的交换,并以源项的形式出现在连续相的控制方程中。同时,连续相会对离散相产生影响。这种耦合作用通过交替求解连续相和离散相的主控方程组来实现。
质量源项:

动量源项:
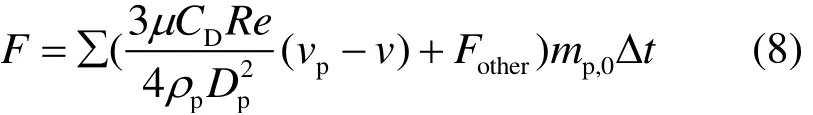
能量源项:
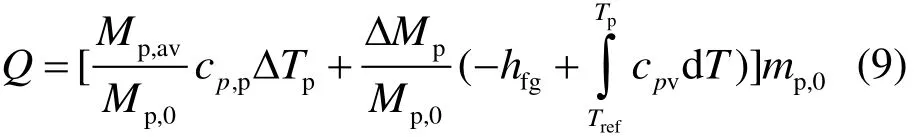
式中:Δt为时间步长,s;cp,p为水滴比热容,J/(kg·K);Mp,0为水滴的初始质量,kg;cpv为水蒸气比热容,J/(kg·K);mp,0为液滴初始质量流率,kg/s;ΔTp为控制单元内液滴的温度改变值,K;Mp,av为控制单元的平均质量,kg;ΔMp为控制单元体内液体的质量变化量,kg。
1.4 边界条件
1.4.1 近壁面边界条件
在填料区域,利用壁面函数法对各个输运方程进行处理,从而来实现水膜与空气的传热传质过 程[11-12]。对于充分发展的湍流运动,其壁面区可以分为黏性底层、过渡层和对数律层。为了更好地表达壁面区的流动,可以引入2个无量纲数,即u+用来表示速度,y+表示网格距壁面的距离:

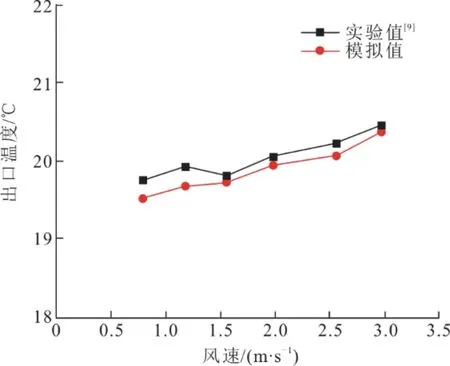
式中:u为流体的时均速度,m/s;τw为壁面切应力,N;Δy为到壁面的距离,m;uτ为壁面摩擦速度,m/s。对于y+<5时,流体在粘性底层,其速度的分布特点是沿壁面法线方向呈线性分布即u+=y+。当60 式中:k为Karman常数;B与E为与表面粗糙度有关的常数;对于光滑壁面,k=0.4,B=5.5,E=9.8[13]。 1.4.2 能量方程中温度的计算 在能量方程中的温度计算,壁面函数定义一个新的无量纲温度T+[14]: 式中:Tp是与壁面相邻第一层网格节点P的温度,K;Tw是壁面温度,K;kp为节点P的湍流动能,J/kg;qw是壁面上的热流密度,J/(m2·s)。 与壁面相邻的第一层网格节点的温度满足对数分布律,即 1.4.3 组分浓度的计算 对于组分输运方程使用壁面函数法,其方法与温度计算方式相似,组分的壁面律可表示为 式中:Yi为某一组分的浓度,mol;Sc和Sct分别为分子施密特数和湍流施密特数;Ji,w为组分i的组分扩散通量。 1.4.4 对于湍流动能与耗散率方程 湍流动能k及其耗散速率ε,在方程中被认为是源项,根据局部均衡假设进行计算。在此假设下,在壁面与相邻区域的控制体积内的湍流动能Gk和耗散速率εp相等,因此可根据对数定律对其进行计算。 式中:U为无量纲速度。 1.4.5 进口与出口边界条件 进口的边界条件选取速度入口。值得说明的是,组分守恒方程中的某一组分的质量浓度Cv,在本文指的是水蒸气的质量浓度。进口空气的水蒸气质量浓度可以利用Cv=Xa1/(1+Xa1)确定。其中,Xa1为进口空气的含湿量,kgv/kga。 湍流动能由k=2(uoI)2/3计算得到。其中:uo为进口空气流速,m/s;I为湍流强度,在此取5%。对于湍流耗散率ε,由公式ε=(cμ3/4k3/2)/l进行计算。其中:cμ=0.09;l为填料特征长度。 出口边界条件为压力出口,设置为标准大气压,即101 325 Pa。 前已述及,文献[9]对填料双层布置下蒸发冷却性能进行了实验测试。本文的数值计算模型,通过与文献[9]实验测试结果对比进行验证。不同进风风速下空气经蒸发冷却后的出口温度如图6所示。 图6 实验数据与模拟结果对比(水流量为62 L/(min·m2)) Fig.6 Comparison between the experimental data and the simulation results (water flow is 62 L/(min·m2)) 由图6可知,二者之间的最大误差为1.6%,可见本文建立的数值计算模型可靠。 总体上,模拟的空气出口温度值稍微低于实验值,这是因为在模拟时进行了相关假设。但在实验过程中,难以完全满足上述假设。由于配水系统以及淋水量的问题,难以保证整个填料表面都有一层均匀的水膜且水膜的厚度一致,淋水温度其实是略高于入口空气的湿球温度。故实验时的冷却效率稍低于模拟过程,导致模拟的出口气温值稍微低于实验值。 本文选取入口空气风速1.5 m/s、干球温度27 ℃、湿球温度19 ℃,空气相对湿度为46.9%的工况。对填料双层布置内部的空气动力场、温度场、湿度场进行分析。 15°与45°填料片交界面的速度矢量分布如图8所示。 从图7可以看出:填料内部的空气流动主要沿着15°填料通道方向流动,这主要是由于空气沿水平方向进入通道之后,45°填料通道比15°填料通道的阻力要大,因此绝大部分的空气会从15°的通道通过;空气在45°填料的波峰处风速较大,这主要是由于空气速度场在填料的波峰处进行了叠加使得该处的风速较大;对于2片填料的粘合处(图4),其风速较低,其原因是粘合处后的空间处于背风处,导致其风速较小。 图7 15°与45°填料片交界面的速度矢量分布(x=0) Fig.7 The velocity vector distribution at the interface of 15° and 45° media (x=0) 图8a)和图8b)分别为y-z平面x=-3.5 mm和x=3.5 mm处速度分布云图,其分别表示15°填料片通道截面和45°填料片通道截面,同时截取了填料进口局部速度矢量分布图。从图8可以看出,流体刚进入填料通道时呈现水平流动,经过一段距离后才沿着流道方向流动。虽然考虑了重力的影响,但从速度场的分布来看,重力的影响并不明显。 图8 速度分布云图 Fig.8 The velocity distribution cloud map 对于填料双层布置的中空区域,其在中间部分风速较大,顶部和底部的风速较小。在中空区域,由于第一块100 mm填料的影响,整体的速度方向并非水平,而是沿着15°填料通道流出,这使得中空区域的顶部风速较小。入口空气从左侧进入,模型上下设置为壁面,无空气通过。因此,对于45°填料,其填料底部没有空气进入,导致其风速较小。在15°和45°通道速度场叠加之后,中空区域中间部分的空气速度偏大。 图9为填料不同截面的温度分布云图。从图9可以看出,空气温度沿气流方向逐渐降低。空气在刚进入填料(第一段填料100 mm)时,温度变化剧烈;当空气经过一段距离后,其温度变化逐渐减弱;在第二段100 mm填料的后半段,空气温度几乎不再变化。在100 mm的中空区域仍然有淋水(图2和图4)。淋水区水滴与空气直接接触进行传热传质,进一步冷却空气。因此300 mm填料双层布置相比于200 mm常规填料多了喷淋区的喷淋冷却,其冷却效率要高于200 mm常规填料。从温降的角度来看,空气依次经过100 mm填料、100 mm中空、100 mm填料的温降分别为4.3、1.3、1.6 ℃。填料承担了82.5%的温降,而中空区域承担了17.5%的温降。此外,对比15°和45°通道的温度变化,45°通道的温度下降得更快,这是由于该通道内空气速度较小,换热充分。 图9 填料不同截面的温度分布云图 Fig.9 Cloud map of the temperature distribution in different cross sections of the filter 在数值模拟中,填料内部的空气温度变化主要是由于空气与水膜表面的饱和空气层之间存在温度差和水蒸气浓度差,引起传热传质。在空气刚进入填料时,空气与饱和空气层之间的温度差和水蒸气浓度差最大,传热传质剧烈;随着空气不断流动,温度差和水蒸气浓度差逐渐降低,传热传质能力逐渐减弱。此外,中空区域的淋水区主要是空气与水滴进行传热传质,空气与水滴的换热面积小于填料区域的水膜,且空气与水滴之间的温度差和水蒸气浓度差与第一段100 mm填料相比较小,所以2段填料区的冷却占比与中空区相比较大。 图10为填料不同截面的含湿量分布。 图10 填料不同截面的湿度分布云图 Fig.10 Cloud map of the humidity distribution in different cross sections of the filter 由图10可见,填料内部湿度场的分布与温度场的分布具有一定的相似性,但水蒸气含量沿气流方向逐渐增大。从图10b)和图10c)可以看出,随着空气的流动,空气中的水蒸气含量变化逐渐趋于稳定,且45°填料通道内水蒸气含量比15°填料通道变化更快。 空气流经填料时与填料上的水膜直接接触,在贴近水膜的地方,存在一个温度等于入口空气湿球温度的空气边界层。由于边界层内水蒸气分子浓度大于周围空气的水蒸气分子浓度,则由边界层进入周围空气中的水蒸气分子数多于由周围空气进入边界层的水蒸气分子数,引起传质,空气的含湿量逐渐升高,导致其边界层与周围环境的含湿量之差逐渐降低,因此气-水间的传质能力沿空气流动方向逐渐降低。 本文建立了三维数值计算模型,模拟研究了填料双层布置下蒸发冷却系统内气-液间的热质传递过程,主要结论如下: 1)填料内部的空气流动主要沿着15°填料通道方向,填料双层布置的中空区域,其在中间部分风速较大,顶部和底部的风速较小。 2)在风速1.5 m/s、入口空气温度27 ℃、湿球温度19 ℃的工况下,空气依次经过100 mm填料、100 mm中空、100 mm填料的温降分别为4.3、1.3、1.6 ℃;所有填料区承担了82.5%的冷却,而中空区域承担了17.5%的冷却。 3)随着空气的流动,空气中的水蒸气含量变化逐渐趋于稳定,且45°填料通道内水蒸气含量比15°填料通道变化更快。 后续将对填料双层布置时的中空区域尺寸进行深入分析,并将填料双层布置下的蒸发预冷系统与空冷塔结合,研究进风预冷对空冷塔换热性能的提升效果。
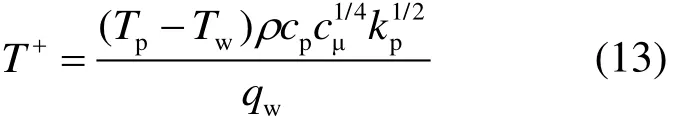

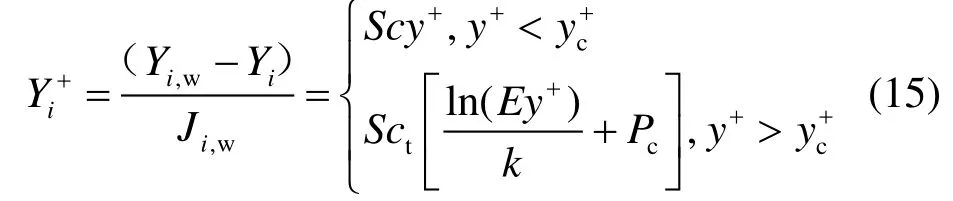
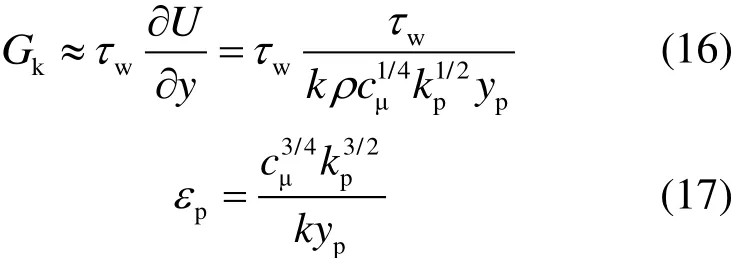
1.5 模型验证
2 结果分析
2.1 空气动力场
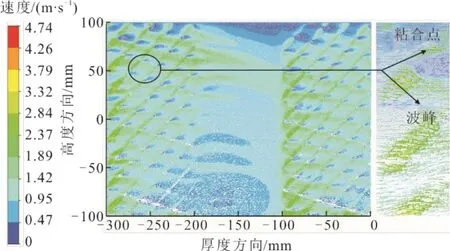

2.2 空气温度场
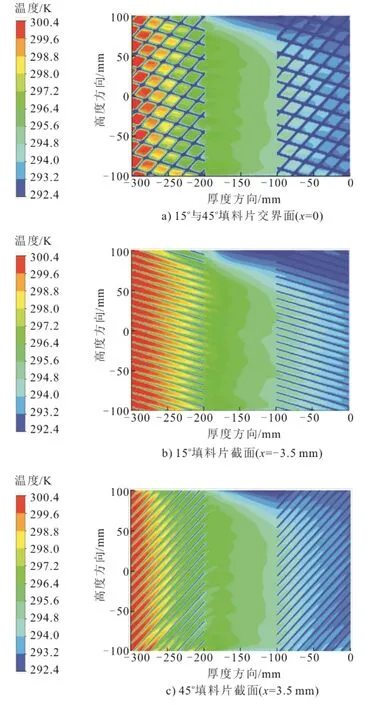
2.3 空气湿度场
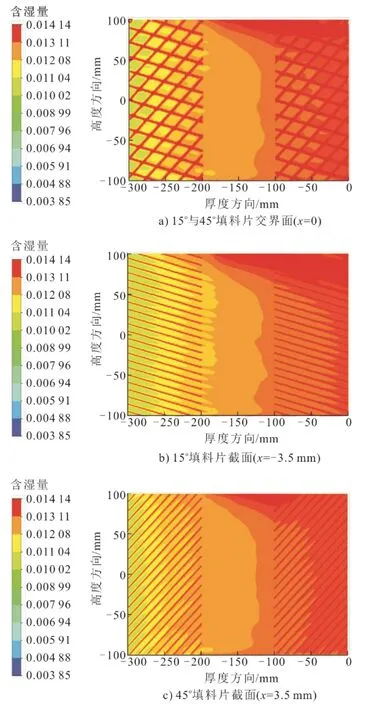
3 结 论
