空冷凝汽器椭圆翅片管管内传热与流动 特性分析
2022-03-25曹国庆潘翔峰王卫良
曹国庆,潘翔峰,吴 哲,王卫良,邓 慧
(1.吉林电力股份有限公司,吉林 长春 130022; 2.吉林电力股份有限公司白城发电公司,吉林 白城 137000; 3.暨南大学能源电力研究中心,广东 珠海 519070)
直接空冷凝汽器由于节水效果好,在我国富煤缺水地区火电机组上得到广泛应用[1-2]。直接空冷凝汽器使用椭圆型或扁平型光管为核心管,在核心管外套接或钎焊翅片构成换热器基管。基管的传热特性决定了空冷凝汽器整体凝结性能。深入研究基管的热动力学特性,对于优化凝汽器的设计与制造,提升在运空冷机组冷端的安全与能效水平,有重要的理论价值与工程意义。
翅片管空气侧的对流换热系数(heat transfer coefficient,HTC)要远低于蒸汽侧凝结对流换热系数,空气侧换热是翅片管性能的最大瓶颈[3-6]。虽然蒸汽侧对凝汽器性能的影响不如空气侧,但依然不可忽视。近年来,有更多研究开始关注基管管内的热动力学行为,如管束蒸汽分布[7]、管内压降[8-9]、两相流动特性[10]、凝结率[11]、逆流管溢流[12]、不凝性气体影响[13]、蒸汽侧热阻[14-15]以及全工况换热性能[16]等。
准确预测管内换热和流动的主特征量,是分析基管管内特性的先决条件。在以往研究中,管内凝结对流换热系数计算一般采用经验关联公式,无标准可循,不同公式计算对流换热系数的结果相差巨大[15]。基于傅立叶(Fourier)定律对热流密度的原始定义,探究翅片管管内对流换热系数的范围和变化规律,依然有重要意义。此外,几乎所有过往研究都采用集总参数理论假设,在恒温壁下估算对流换热系数[11,13],蒸汽和冷却空气间的换热量也一般通过经验方法如效能-传热单元数(effectiveness- number of transmission units,ε-NTU)法[14-15]和对数平均温差(logarithmic mean temperature difference,LMTD)法[16]估算。也即,管壁温度以及关联公式相关系数,被视为输入条件而不是输出结果,这就忽略了凝汽器基管的散热;同时取决于蒸汽和冷却空气传热与流动的物理现实,即翅片管内外工质在流动边界上的温度、热通量以及NTU或LMTD不能由单侧工质预先确定,而是取决于工质对之间耦合换热的结果。最后,以往大多数管内研究的重点[9-15],在于分析管深方向上热力学量的变化规律,对管宽方向即空气流向上的发展变化关注较少。而工程应用的椭圆管与大扁管,都是大宽高比管型对象,在管宽方向的热动力学行为尚待研究。
本文以椭圆翅片管为研究对象,基于直接空冷凝汽器换热基管的分布参数热力学特征[17-18],建立翅片管耦合换热数学模型,通过数值求解,分析管内换热与流动在两相流与冷却空气流向上的变化规律,并给出可视化结果。研究方法与结果有利于深入了解凝汽器基管内换热与流动,有助于凝汽器翅片管的优化设计与制造。
1 数学模型和数值方法
1.1 耦合换热模型
工程椭圆翅片管研究对象来自某超临界660 MW机组凝汽器。该凝汽器由8排冷却单元列组成,每列共8个冷却单元,各单元采用3排翅片管。核心管为椭圆管,材料为碳钢外包铝;外覆椭圆形状环翅片,材料为铝。顺流冷却单元换热性能为:在设计大气温度下,凝结热耗保证(turbine heat- acceptance,THA)工况汽轮机80%饱和蒸汽。工程管的几何尺寸见表1。
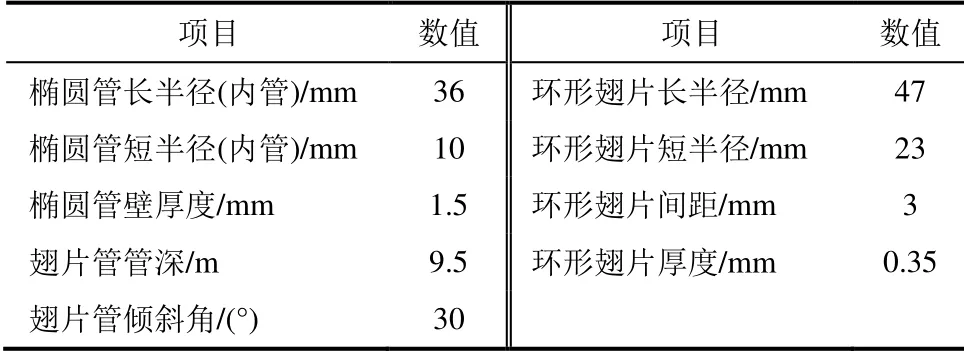
表1 工程翅片管几何尺寸 Tab.1 Geometric parameters of an engineering finned tube
基于工程翅片管对象实际倾角下的管宽、管深、管高几何方向,定义局部坐标系(local coordinate system,LCS)x、y、z方向,描述了3-D形式下工程翅片管空气侧与蒸汽侧工质流动,如图1a)所示。进一步地,以2-D形式给出了工程翅片管工质对的耦合换热过程,如图1b)所示。
为描述图1b)中椭圆管内液膜表面凝结的热质传递,利用多相流理论中的流体体积(volume of fluid,VOF)方法[19]建立两相流连续方程,基于Lee模型[20]估算相变过程中的质量转换。Lee模型方程中的相变系数r设置为1 000 000 s-1,以相变质量构成连续方程的源项[21-23],由此计算汽化潜热,构建能量方程的源项。利用Fourier方程描述图1b)中由椭圆管内壁到管外壁再到环形翅片的热量传导;用连续、Navier-Stokes和能量方程建立图1b)中冷却空气与环翅外壁的对流换热模型;用剪切力传递(shear stress transport,SST)k-ω方程[24]描述翅片管内外工质流动的湍流效应。以上热流过程模型的方程列于表2。
表2方程分别描述了图1b)独立换热区域内蒸汽凝结、金属热传导和空气对流。为耦合以上3种换热过程,提出热流密度和温度在交界面上处处相等的边界条件,以求解各区域的热流方程。交界面的具体位置如图1b)所示。
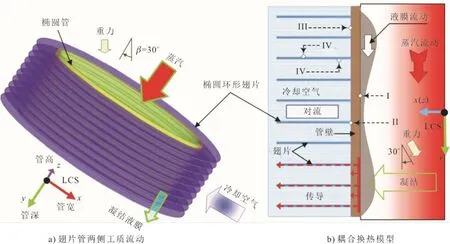
图1 椭圆翅片管流动工质对与耦合换热模型 Fig.1 Schematic diagram of working fluid of oval finned tube and the coupled heat transfer model

表2 耦合换热模型的方程 Tab.2 Equations of the coupled heat transfer model
1.2 数值方法
按工程翅片管几何尺寸,用ANSYS ICEM®14.0[25]建立翅片管与计算域数值模型。受限于计算工作站性能,数值翅片管的管深减少到工程管1/10,设定为1 m,其他尺寸维持与工程管一致。
用ANSYS Fluent®14.0[26]完成数值计算。翅片管计算域的边界条件为:蒸汽和空气的入口设置为速度入口,空气和两相流出口设为压力出口,空气域在管深的两端为绝热壁,在高度的两端设为对称 面。使用稳态计算与隐式VOF方法。判敛标准为:能量方程残差小于10-6,其他方程残差小于10-3。在方程收敛或计算时间超过5 s后,直接提取ANSYS Fluent®14.0中的“Static Temperature”“Total Surface Heat Flux”“Surface Heat Transfer Coef.”“Wall shear”结果,分别作为温度、热流密度、对流换热系数以及剪切力进行分析。值得指出的是,ANSYS Fluent®在液膜表面上应用Fourier定律计算显热,再加上相变热量后得到热流密度[26]:
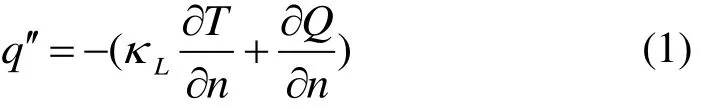
凝结对流换热系数由凝结热流密度以及蒸气与椭圆管内壁之间的温差确定[26]:

1.3 模型与方法验证
针对1 m长椭圆翅片管计算域,对两相流通流截面应用O型网格,在贴壁区加密形成边界层,从贴壁单元高度30 μm的粗网格到高度为2 μm的细网格,验证计算域的网格独立性。无关性指标设为椭圆管内壁平均对流换热系数。验证结果表明,贴壁单元高度2 μm和5 μm之间的指标偏差为1.15%。最终确定计算域采用单元高度为5 μm网格,此时网格数量为7 624 600。图2显示了此计算域下汽轮机THA工况蒸汽流量下贴壁单元到椭圆管内壁的无量纲值距离(y+)。
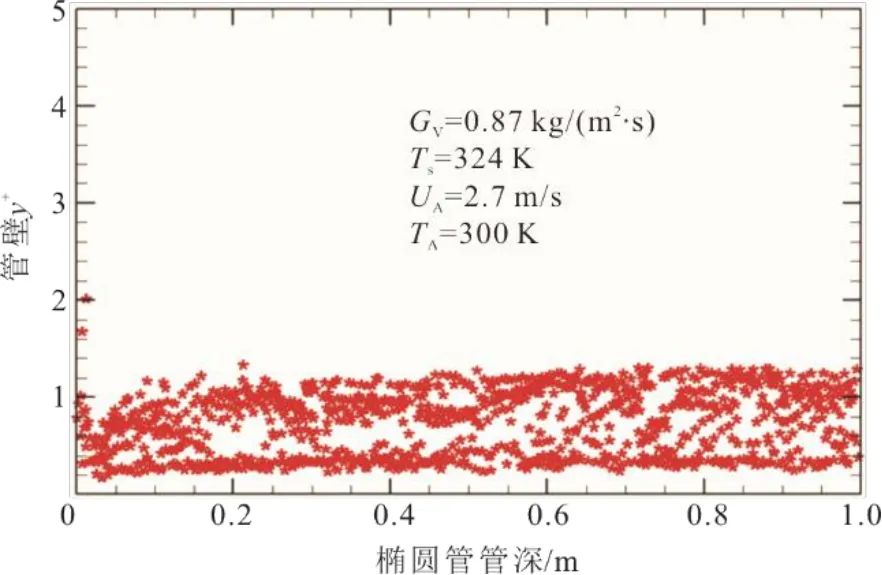
图2 椭圆管计算域贴内壁网格y+沿管深变化 Fig.2 Variations of y+ of oval tube calculation domain along the tube depth direction
由图2可见:绝大多数单元网格单元的y+小于1.5,表明计算域可准确计算膜状凝结数学模型中的流动和换热方程。
忽略管内蒸汽凝结换热,将椭圆管内壁设置为等温壁,壁温在324~340 K变动,冷却空气入口温度在280~320 K变动,冷却空气流速固定为2.7 m/s。通过对比环形翅片外表面对流换热系数数值结果与工程管冷却空气流速2.7 m/s时空气侧对流换热系数标称值,验证模型模拟空气侧对流换热的有效性,结果如图3所示。由图3可见,10个算例对流换热系数数值解稳定在47 W/(m2·K)左右,大于标称值(40 W/(m2·K))约17.5%,数值解与标称结果匹配良好。
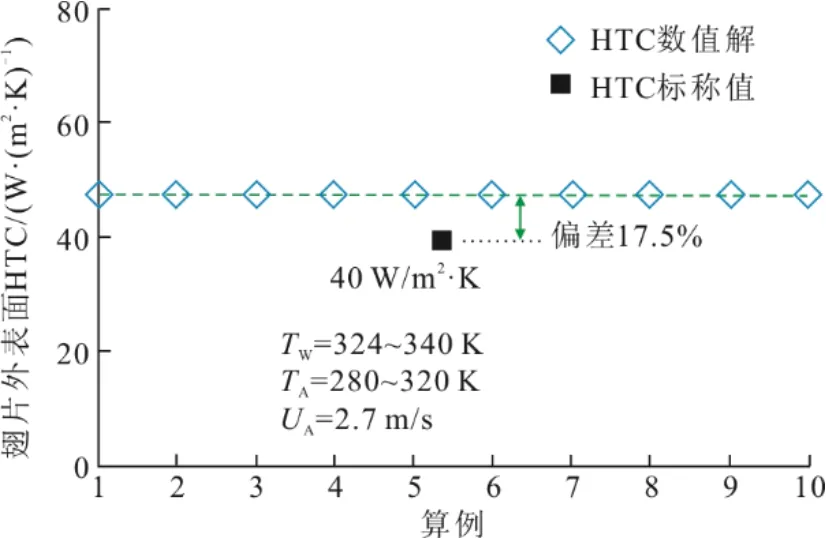
图3 翅片管空气侧对流换热系数数值解与标称值对比 Fig.3 Comparison between predicted and nominal heat transfer coefficient on the air side of finned tube
忽略管外空气对流换热,将椭圆管外壁设置为370 K等温壁,蒸汽入口温度为373 K,椭圆管管深10 m。通过对比椭圆管内壁对流换热系数数值结果与凝结对流换热系数的3个常用经验公式计算值[27-29],验证模拟蒸汽侧凝结换热的有效性,结果如图4所示。由图4可见,除去蒸汽入口1 m管段,对流换热系数的数值解与Shah[27]和Nusselt[28]公式结果吻合良好,误差在15%以内。
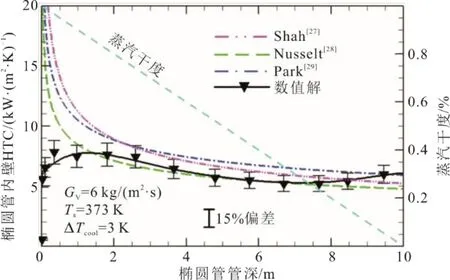
图4 翅片管蒸汽侧对流换热系数数值解与经验公式计算值对比 Fig.4 Comparison between predicted and empirical formula calculated convective heat transfer coefficient on the vapor side of finned tube
2 数值结果与讨论
椭圆翅片管入口工质热力参数见表3。

表3 椭圆翅片管工质入口热力参数 Tab.3 Thermodynamic parameters of the fluid at inlet of the oval finned tube
蒸汽入口压力和温度设置为13 kPa和324 K,与我国典型600 MW机组THA工况下凝汽器蒸汽入口参数保持一致。在THA工况下,顺流翅片管蒸汽质量流量约为5.6 kg/(m2·s)。考虑数值管深为工程管1/10,为确保数值管过流凝结,将其入口流量设置为0.87 kg/(m2·s),超过实际流量1/10,对应蒸汽流速10 m/s (UV=GV/ρV)。冷却空气入口流速设置为2.7 m/s,与工程管一致。
2.1 椭圆管内换热特性分析
用表3所列冷热工质入口条件,对1 m管深椭圆管翅片管进行数值计算,得到椭圆翅片管内壁温度、热流密度、对流换热系数云图如图5a)—图5c)所示。图中还标注了全局坐标系(global coordinate system,GCS)的X、Y、Z方向。
由图5a)—图5c)可见,内壁温度在蒸汽入口出现低温区,热流密度沿冷却空气方向下降明显,对流换热系数在椭圆长径中点区域出现低谷区。为定量分析翅片管内的换热特性,给出了内壁温度、热流密度、对流换热系数沿管深(即两相流方向)与管宽(即冷却空气方向)上的变化特性,结果分别如图6与图7、图8与图9、图10与图11所示。椭圆翅片管的管深与管宽方向定义以及冷热工质的流向示意见图1。
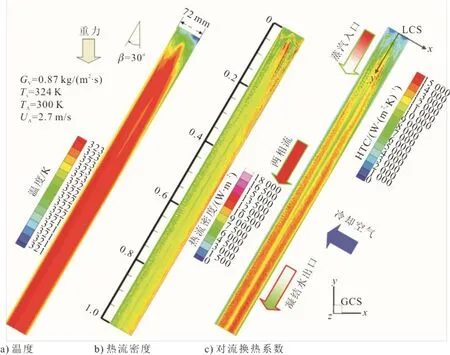
图5 椭圆管内壁温度、热流密度及对流换热系数云图 Fig.5 Cloud map of temperature, heat flux and convective heat transfer coefficient on inner wall of the oval tube

图6 椭圆管内壁温度沿两相流方向变化 Fig.6 Variation of temperature on inner wall of the oval tube with two-phase flow
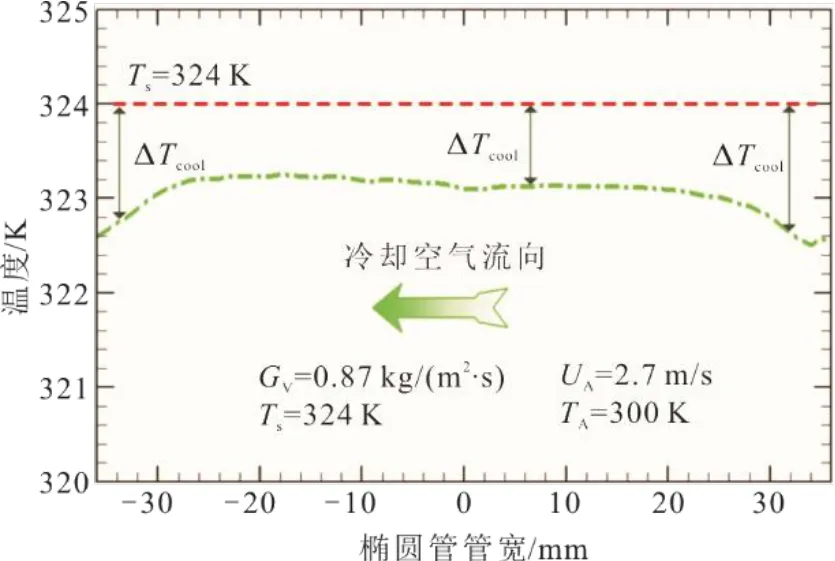
图7 椭圆管内壁温度沿冷却空气方向变化 Fig.7 Variation of temperature on inner wall of the oval tube with cooling-air flow
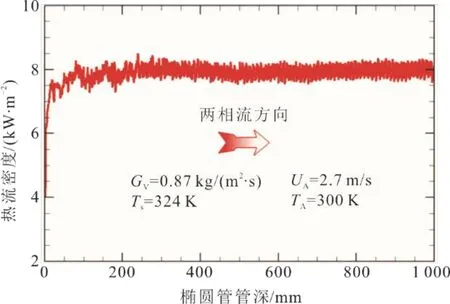
图8 椭圆管内壁热流密度沿两相流方向变化 Fig.8 Variation of heat flux on inner wall of the oval tube with two-phase flow

图10 椭圆管内壁对流换热系数沿两相流方向变化 Fig.10 Variation of convective heat transfer coefficient on inner wall of the oval tube with two-phase flow
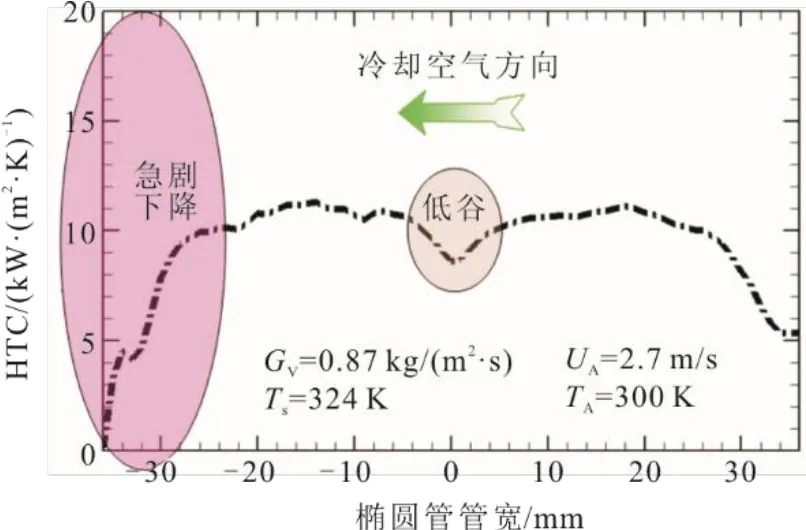
图11 椭圆管内壁对流换热系数沿冷却空气方向变化 Fig.11 Variation of convective heat transfer coefficient on inner wall of the oval tube with cooling-air flow
由图6可见:沿管深方向,椭圆管的内壁温度在凝结管入口有明显低温区,过冷度为3 K左右;随着两相流在管内持续相变凝结,过冷度减小并稳定在1 K内。由图7可见,沿管宽方向,温度在环形翅片的空气入口与空气出口区域稍低,整体而言,管壁过冷度稳定在0.8 K左右。
由图8可见,沿管深方向,椭圆管内壁热流密度在凝结管入口极短区间内急剧增长,然后迅速稳定在8 kW/m2左右,并沿全凝结管段基本不变。由图9可见,沿管宽方向,热流密度随管外冷却空气在环形翅片内的持续流动与吸热不断减小,在冷却空气入口与出口,热流密度急剧下降;另外注意到,在翅片冷却空气出口的极短区间内,热流密度下降为0,表示在椭圆上半部分的极顶端无蒸汽凝结。
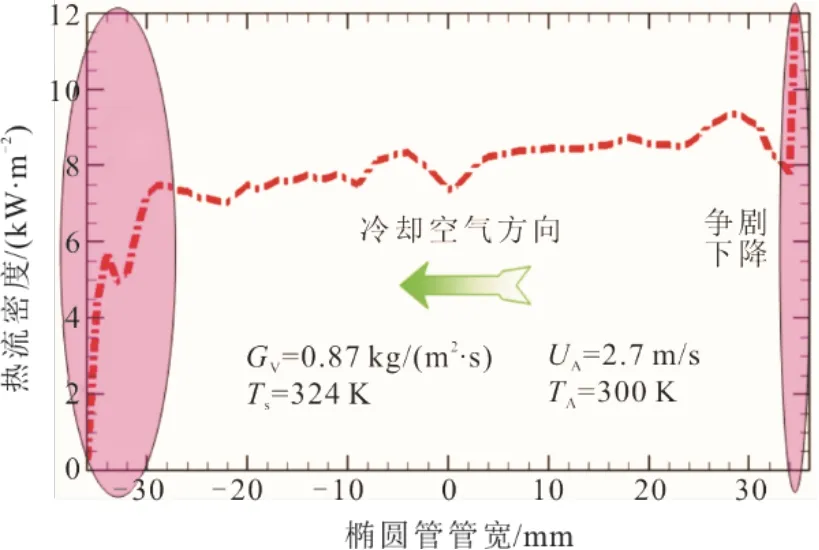
图9 椭圆管内壁热流密度沿冷却空气方向变化 Fig.9 Variation of heat flux on inner wall of the oval tube with cooling-air flow
由图10可见:对流换热系数数值解在300~ 700 mm管段,与Park[29]值吻合较好;从500 mm到椭圆管出口,其数值解与Nusselt[28]和Shah[27]值更为接近,误差均在15%以内;但随着两相流沿管深持续凝结,数值解没有像3个经验公式值一样,出现下降趋势,甚至从中间管段开始,缓慢增长。以上趋势偏差是由于对流换热系数计算方法的不同导致[10,30]:数值解由热流密度和饱和蒸汽/管壁之间的过冷度确定,而经验公式结果完全依赖于管深度、蒸汽干度和液膜雷诺(Reynold)数。
由图11可见:沿管宽方向,内壁对流换热系数在椭圆管长径中点区域出现明显低谷区,并以低谷为中心左右对称;在冷却空气出口的狭隘区间内,对流换热系数急剧下降直至0。
2.2 椭圆管内流动特性分析
用表3所列冷热工质入口热流条件,对1 m管深椭圆管翅片管进行数值计算,得到椭圆翅片管内壁液相的VOF云图,如图12所示。
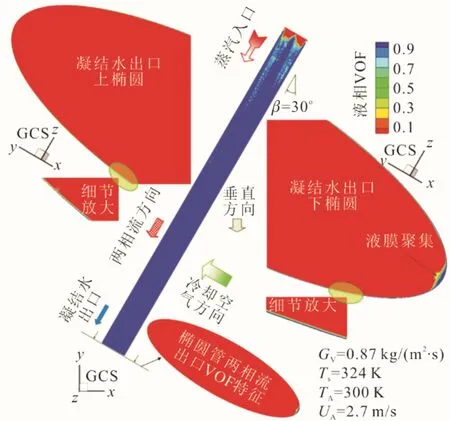
图12 椭圆管内壁液相VOF云图 Fig.12 VOF cloud diagram of liquid phase on inner wall of the oval tube
由图12可见:除了蒸汽入口的狭隘区域,椭圆管全段被凝结液膜覆盖;在凝结管出口截面上,液膜在椭圆下半部分极顶端,有明显聚集。根据Mishima两相流流型判据[31],椭圆管内的两相流型可定性为环状流。
为定量分析翅片管内流动特性,分别给出了液膜厚度沿管深与管宽方向的变化特性,如图13、 图14所示。

图13 椭圆管内壁液膜厚度沿两相流方向变化 Fig.13 Variation of thickness of liquid film on inner wall of the oval tube with two-phase flow
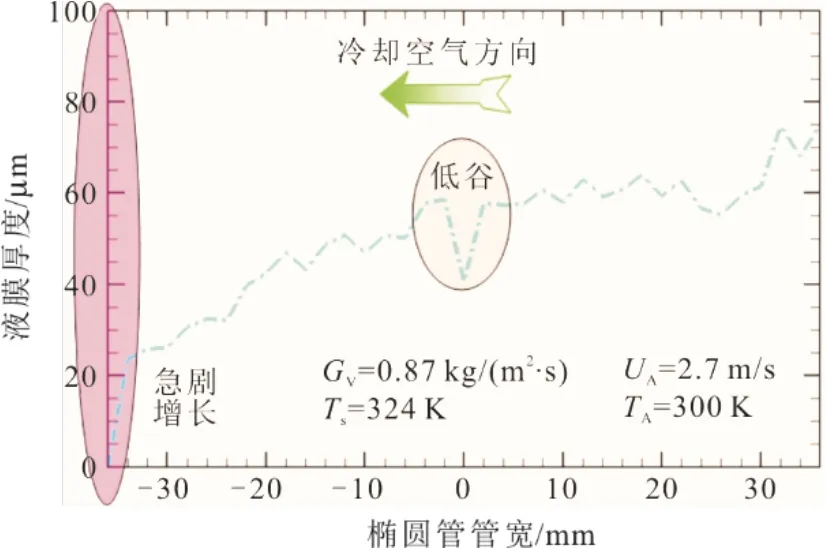
图14 椭圆管内壁液膜厚度沿冷却空气方向变化 Fig.14 Variation of thickness of liquid film on inner wall of the oval tube with cooling-air flow
由图13可见:沿管深方向,液膜在凝蒸汽入口100 mm管段内急剧增长;随着蒸汽在管内持续凝结,从40 μm稳定增长至80 μm左右;由于出口扰流影响,在出口区间有明显波动出现。
由图14可见:逆冷却空气流动方向,在冷却空气出口的狭隘区间内,液膜厚度从0急剧增长至 20 μm,并沿管宽方向表现出增长趋势;但在椭圆管长径中点区域,有明显低谷区出现。在椭圆管倾角、长短半径比以及管壁粗糙度相对固定的前提下,以上低谷区的出现,可能与气液界面剪切力、液膜重力与液膜表面张力之间的相互作用有关,但低谷区出现的明确导因,还需更进一步探究。
用表3所列冷热工质入口热流条件,对1 m管深椭圆管翅片管进行稳态数值计算,得到椭圆翅片管内壁剪切力云图,如图15所示。
由图15可见,按GCS定义方向,Y向与X向剪切力皆为负,表示液膜在蒸汽流动与重力作用下,沿重力方向与逆冷却空气流动方向,朝凝结出口与椭圆下半部分极端方向流动。
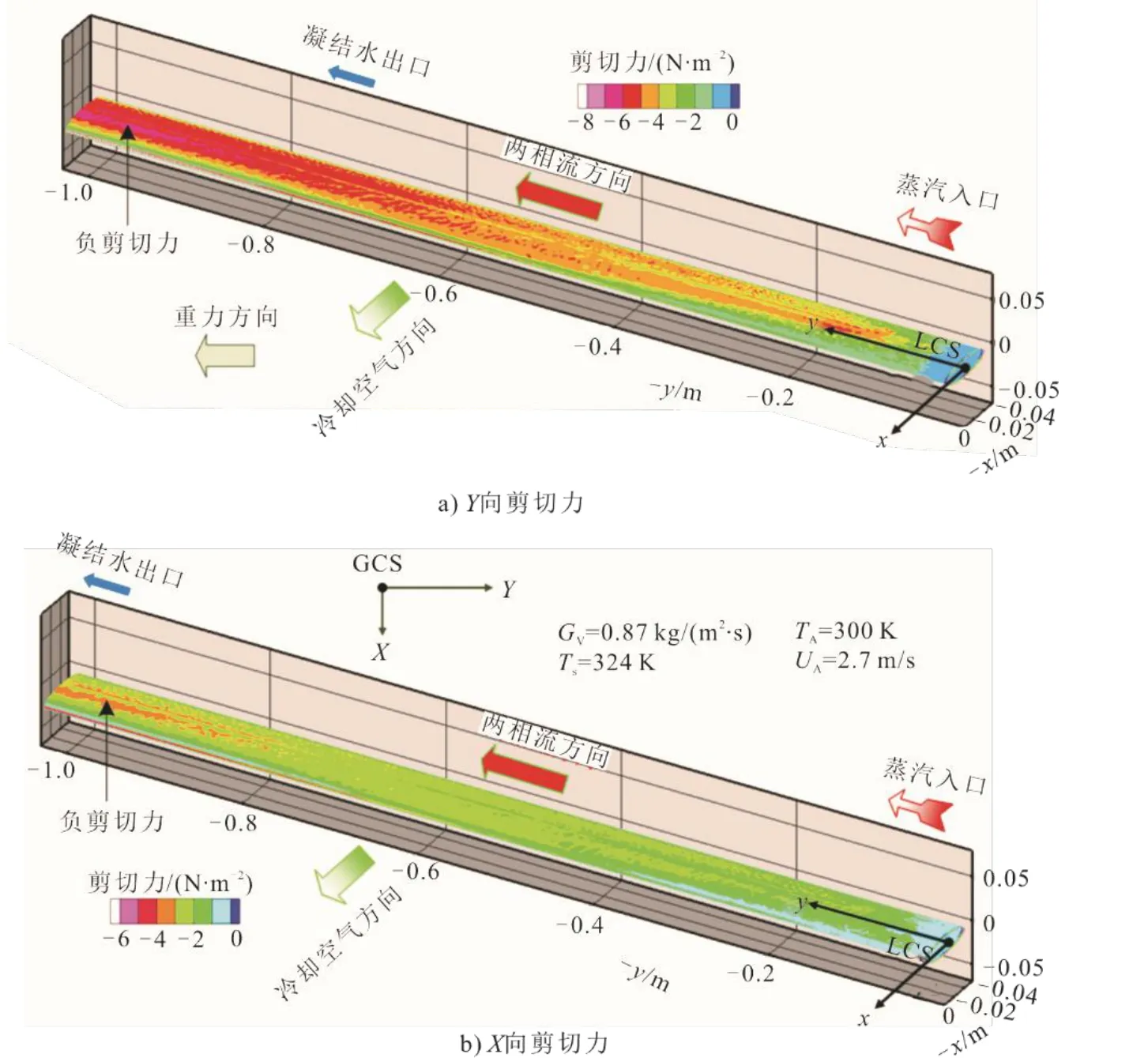
图15 椭圆管内壁剪切力云图 Fig.15 Cloud map of shear on inner wall of the oval tube
为定量分析管内流动特性,分别给出了Y向与X向剪切力沿管深与管宽方向的变化特性,如图16、图17所示。
由图16可见,在管深方向,随着蒸汽在管内持续凝结,Y向剪切力绝对值从0稳定增长至4 N/m2,表示液膜在蒸汽剪切力和重力作用下,沿两相流方向加速流动。
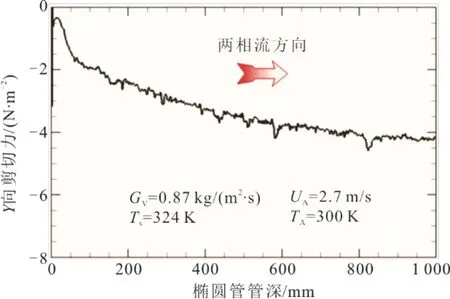
图16 椭圆管内壁Y向剪切力沿两相流方向变化 Fig.16 Variation of Y-shear on inner wall of the oval tube with two-phase flow
由图17可见:逆冷却空气流动方向,以椭圆长径中点为分界线,X向剪切力绝对值从0稳步增至2 N/m2,然后又减小到1 N/m2,表示液膜在椭圆上半部分加速流动,而在下半部分流速趋缓;在椭圆下半部分极端区域,X向剪切力绝对值从1 N/m2急剧增至3 N/m2,结合液相VOF云图(图12)可知,由于液膜在此区域的聚集,导致流动明显加速。
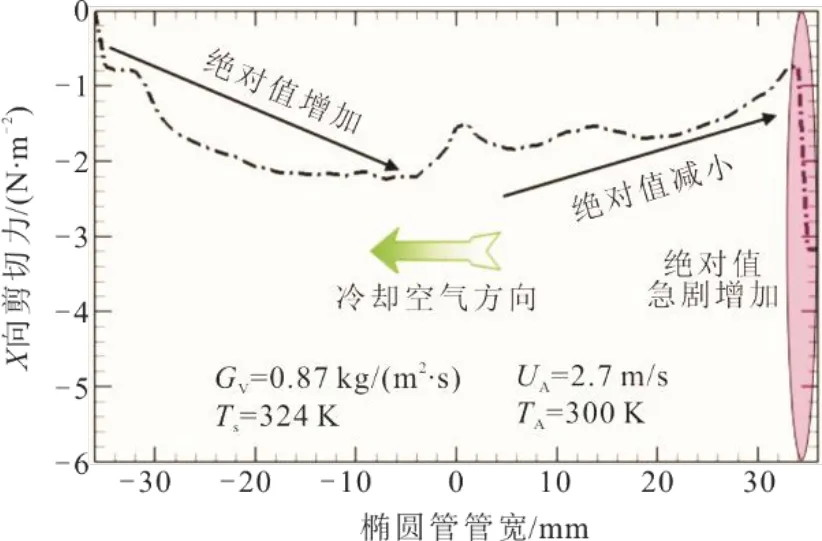
图17 椭圆管内壁X向剪切力沿冷却空气方向变化 Fig.17 Variation of X-shear on inner wall of the oval tube with cooling-air flow
3 结 论
1)管内热力学特征量沿两相流流向即管深方向变化较为平缓,但沿冷却空气流向即管宽方向变化剧烈。
2)由于采用Fourier定律计算对流换热系数,管内凝结对流换热系数沿管深方向没有持续下降,甚至有缓慢增长,这与经验关联式计算得到的对流换热系数变化趋势相反,但2种方法计算得到的对流换热系数值非常接近。
3)沿着椭圆管管宽方向,在冷却空气的入口和出口,管内壁热流密度和对流换热系数有明显低谷区域出现,因此可在此区域的翅片侧或管壁侧采用换热增强型结构与材料,提高翅片管的整体性能。
4)尽管红外热像仪、丝网传感器、粒子图像测速仪等实验装置可用来观测凝结管内的壁温、液膜厚度、剪切力和两相流型,但是空冷翅片管核心管的极端狭窄几何结构,使得实验装置的安装应用变得非常困难。因此,利用数值计算研究翅片管内的分布式传热和流动,是有效的科学分析方法之一。
