基于机器视觉的共轴双旋翼桨尖位移实时监测系统

车兵辉，尹欣繁，彭先敏，章贵川

(中国空气动力研究与发展中心，四川 绵阳 621000)

共轴双旋翼直升机具有两个桨毂，在设计上通过减小上下桨毂之间的距离，以减小桨毂阻力。但另一方面，共轴刚性旋翼在飞行状态时需要承受很大的升力偏置载荷，共轴反转的上下旋翼桨叶会发生显著的弹性形变，过小的安装间距可能会导致上下旋翼桨尖发生碰撞，影响直升机的飞行安全[1]。尤其是共轴双旋翼直升机风洞实验中，在前飞状态时需要对旋翼配平，而实验时的一些配平状态是不可预测或预知的，这就增加了上下旋翼桨尖碰撞的风险。因此，在风洞实验时，必须对共轴双旋翼的桨尖间距进行实时测量和监测。当桨尖距离小于预警值时，应立即对旋翼实验系统紧急停车，防止旋翼实验台设备的损伤或者威胁人员安全。

由于直升机旋翼桨叶的桨尖位移测量是在旋翼高速旋转动态下进行的，许多静态的测量方法难以适应高速下的实时测量。我国共轴刚性双旋翼直升机的相关实验研究起步较晚，共轴刚性双旋翼直升机研究主要集中在气动特性[2]、配平操纵[3-4]、载荷[5]等方面，对桨尖偏移或桨叶变形测量相关实验研究较少。但近年来，对单旋翼桨尖位移测量方法的研究成果较多，文献[6]～文献[10]中均通过在桨尖下表面或上表面粘贴标记点，采用了机器视觉的立体测量方法,这种方法测量精度较高,但系统复杂、实时性差。运用高速摄影系统对单旋翼直升机桨尖运动轨迹进行测量，取得了较好效果[11]。由于双旋翼旋转时上下旋翼桨叶会彼此遮挡，现有方法并不能直接应用于运动过程中上下旋翼桨尖位移的测量。

共轴双旋翼实验具有高风险性，且桨尖测量不能影响实验开展。因此，结合单旋翼桨尖位移测量的立体视觉测量方法，提出了一种单相机视觉测量的非接触式双旋翼桨尖距离实时监测方法。该方法结构简单，能够满足实时性和精度要求，对保障共轴双旋翼实验的安全具有重要意义。

1 系统总体方案

1.1 系统设计要求

实验采用4 m直径的共轴刚性双旋翼实验台，实验条件及工况如表1所示。

表1 实验条件及工况

结合实验条件和工况，以及安全监测目的，提出以下设计要求。

① 图像实时采集和显示。由于实验状态复杂，具有一定的危险性，需要对旋翼桨尖位移进行实时监测，所以必须对获取的每一帧桨尖原始图像和经过图像处理辨识出的待测目标点图像实时显示，有利于观测获取的图像质量，保证待测目标点在视场范围内以及图像处理算法的有效性和可靠性。

② 上下旋翼间距实时显示。由于实验具有高风速和高转速特点，操纵参数多且具有一定的探索性，在复杂的实验状态下，桨尖位移变化范围不可预知，必须对获得的每一帧图像进行实时处理，计算出上下旋翼桨尖距离并显示出来，时刻关注桨尖间距变化情况。

③ 适应不同实验条件及工况。由于实验条件复杂，且具有不同风速和转速、配平参数的组合，系统必须在不断变化的实验条件下，获取高质量的图像，并能准确分辨出目标点，计算出桨尖距离，这就要求系统能够实时调整图像采集参数和图像处理参数，以保证不同实验条件下得到准确结果。

1.2 系统组成

系统主要包括硬件和软件两个部分。硬件系统主要包括获取图像的高速相机、增强反光标记点亮度的LED灯、确定每片桨叶位置并触发相机采集的传感器以及控制相机并对图像进行处理的计算机；软件功能主要包括相机控制、桨尖图像的实时处理、图像和曲线显示、参数设置等功能。系统结构如图1所示。

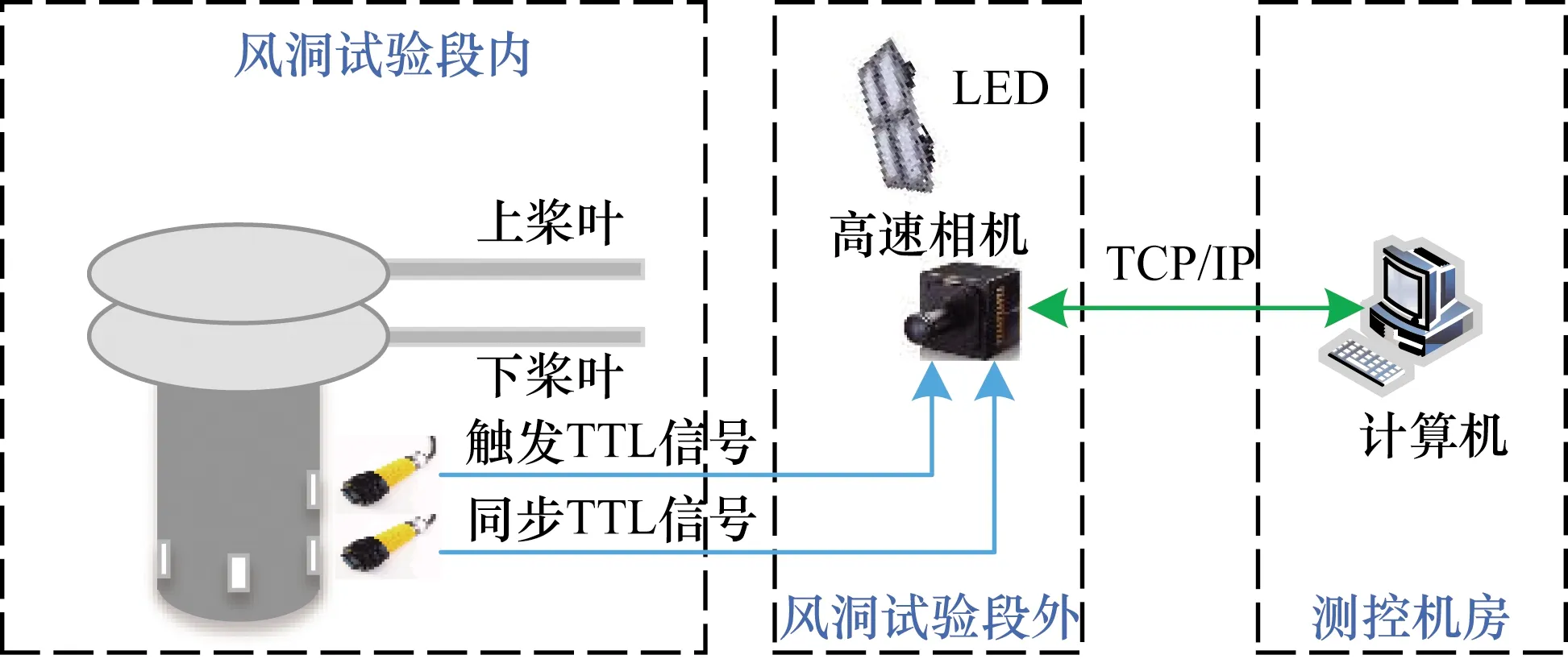
图1 系统结构组成

1.3 系统工作原理

基于视觉测量的桨尖距离监测系统是在桨叶桨盘某一方位桨尖正方向安装一台高速相机，在旋翼旋转过程中，当桨叶通过此位置时，安装于桨毂上的转速传感器会产生一个脉冲，触发相机采集图像，然后通过数字图像处理算法对获取的图像进行处理，获取每张桨尖图像中的桨尖中心的坐标，通过坐标到位置的转换计算桨尖中心点的位置。上下桨叶桨尖位置的差值即为桨尖距离，并将原始图像和桨尖距离实时显示在界面上，便于工作人员监测。

2 系统硬件设计

硬件系统是获取满足要求的图像的关键，由于所测对象是高速旋转的，因此对硬件系统有特殊要求，需要根据系统的功能和技术要求对硬件系统进行设计和选型。硬件系统主要包括工业相机、镜头、光源、桨叶位置传感器等。

2.1 相机选型

相机负责采集桨尖图像，由于直升机旋翼实验转速较高，每一转都要多次采集图像，相机必须具有较高的帧率以满足高转速下桨尖图像的采集。4 m直径的共轴刚性双旋翼实验台最大转速为900 r/min，有4片桨叶，每转需要采集4次，则每秒钟产生60帧图像，因此相机在外触发工作模式下要达到60帧以上的帧率。相机的分辨率决定了测量的精度，因此需要选择较高分辨率的相机以满足测量精度。由于旋翼的高转速，桨尖的线速度非常快，每片桨叶经过视场的时间非常短，这就要求相机具有很短的曝光时间，否则获得的图像就会模糊，为后续的图像处理带来困难，相机的曝光时间通常与帧率有关。综上所述，综合考虑帧率、分辨率、曝光时间、数据传输速率等参数，所选择相机的主要参数如表2所示。

表2 相机参数

2.2 镜头选型

摄像系统中镜头决定了系统的视场大小，既要保证目标在视场范围内，又要保证目标位移具有足够的分辨率，因此镜头的选取综合考虑视场大小和目标位移的大小。在实际应用中，待测目标应远离视场边缘，避免图像产生畸变，因此在计算视场大小时应留一些余量。所需镜头的焦距可按式(1)计算。

f=LHc/Hv

(1)

式中：f为镜头焦距；L为相机到拍摄目标的距离；Hc为相机光学成像靶面的高度；Hv为拍摄视场的高度。在实验时L为2 m，根据相机参数可知Hc为20.48 mm,Hv为800 mm，代入式(1)可计算出焦距约为50 mm。因此，选择焦距为50 mm的镜头。

2.3 同步与触发

为了保证每片桨叶进入拍摄视场时采集图像，同时确保每片桨叶在同一位置采集图像，相机采集图像需要通过桨叶位置信号触发和同步相机采集。触发信号用于控制相机开始采集图像，当相机启动后，如果处于外触发模式，则相机等待触发信号，当触发信号到达时，相机才进入采集图像的状态，此时相机并不采集图像，而是等待同步信号的到来；同步信号用于控制相机的快门，每一个同步信号到达，相机就采集一幅图像，此时的帧频由同步信号的频率决定。触发与同步时序如图2所示。选取一个桨叶作为基准桨叶，在该桨叶对准相机的位置处安装光电传感器，并将该信号作为开始采集的触发信号，则采集到的第1幅图像就是基准桨叶。同时另外一个光电传感器检测每一片桨叶对准相机的位置，将该信号作为同步信号。这样采集到的图像序列按照1号桨叶、2号桨叶、3号桨叶、4号桨叶的顺序往复排列，这样就可以分辨出每一片桨叶。

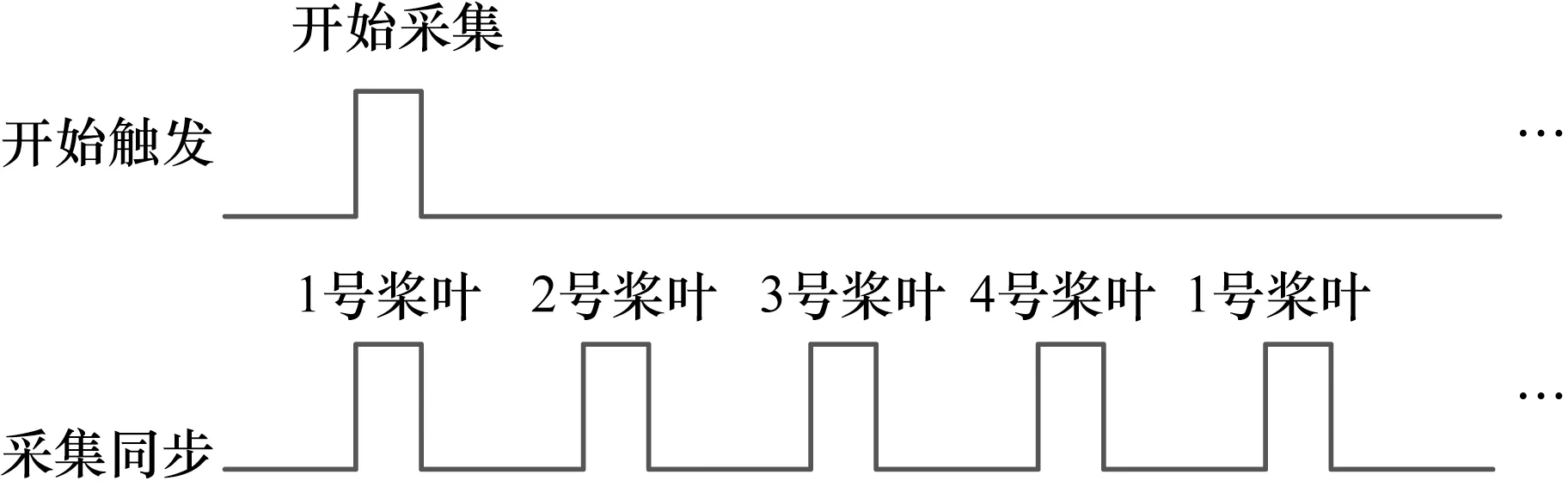
图2 触发与同步时序

采用这种触发和同步方式，保证每片桨叶在同一位置采集，且不同转速状态下，桨叶位置是不会变的，因此这种采集方式与转速不相关，可以适应任何转速状态。

2.4 光源选择

由于系统必须满足旋翼高速旋转工况下的图像获取，要获取清晰的图像，相机曝光时间就必须非常短，否则图像会出现拖影；另一方面当曝光时间非常短时，进入相机内部感光元件的光就会很小，从而使粘贴在桨尖的反光贴图像亮度不够，不适于图像的处理，两者是一个矛盾体。要获得清晰、桨尖明亮的图像，就必须增强光照和反光贴的反光量。因此选用无频闪的大功率LED灯作为补充光源。

2.5 监测位置选取

在实验过程中，上下旋翼在相互重合的位置可能发生桨尖碰撞。上下旋翼最近的位置为270°方位角处[1]，如图3所示。因此相机的拍摄位置对准旋翼270°方位角处。监测此处的桨尖距离，避免上下旋翼桨尖碰撞。

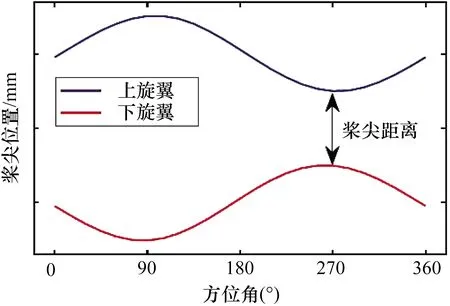
图3 旋翼距离变化趋势(修改图)

3 系统软件设计

共轴双旋翼桨尖位移实时监测系统软件基于Matlab软件平台开发，采用相机厂商提供的API实现相机的控制，并利用Matlab强大的图像处理能力实现图像的实时处理。软件主要包括相机控制与标定、图像采集与显示、参数配置、图像处理、桨尖距离计算与显示等功能，软件运行流程如图4所示。

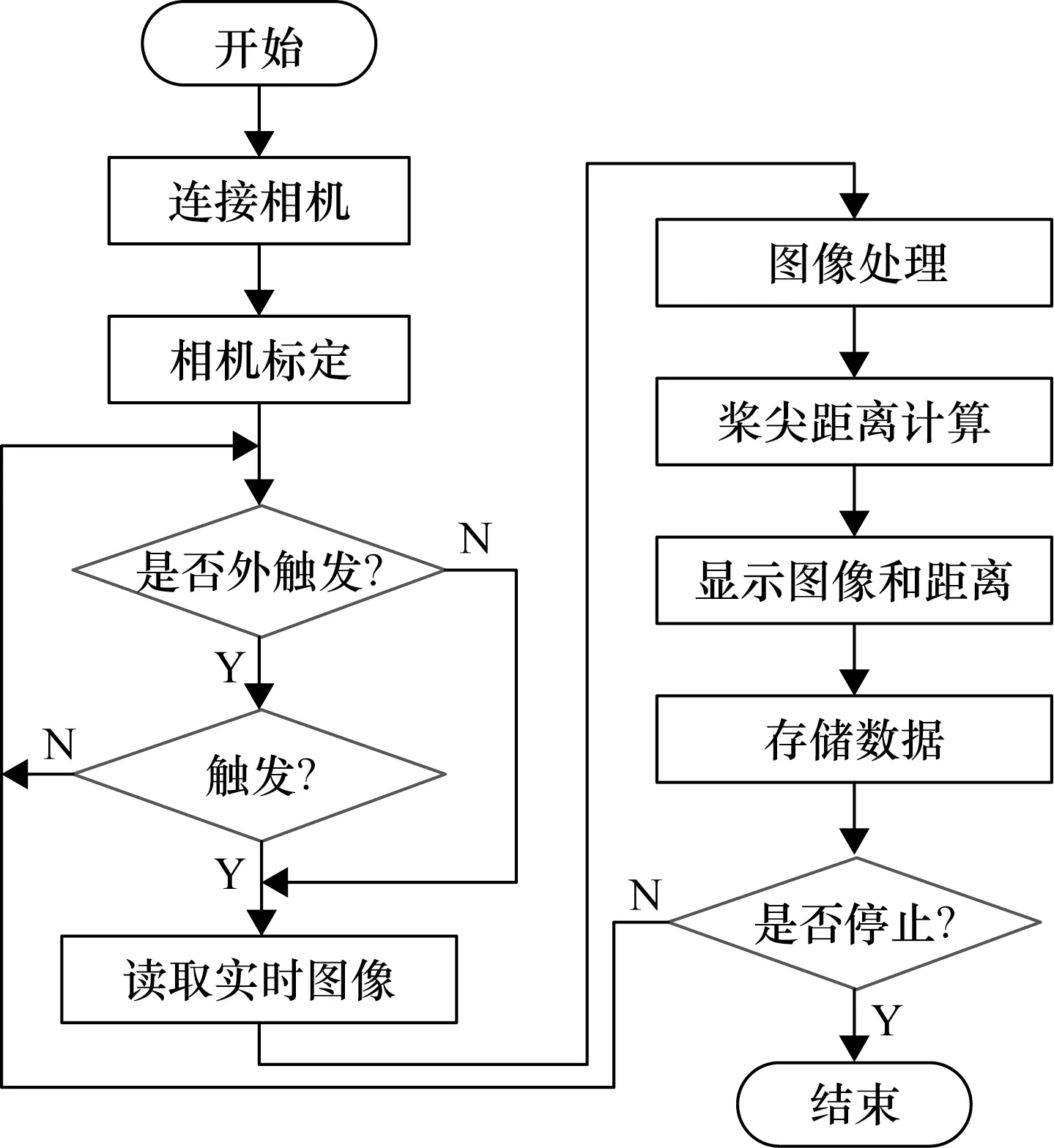
图4 软件运行流程

其中，相机标定和桨尖距离计算是软件的核心功能，也是软件设计的重点。

3.1 相机标定

摄影测量获得的目标点坐标为成像平面坐标系下的像素坐标，要获得被测物体的物理位置，就必须通过标定获得像素坐标系与物理坐标系的转换关系[12-13]。

标定采用棋盘格测量标定方法，棋盘格如图5所示，将棋盘格标定板放置在桨尖正对相机的位置，获取棋盘格标定板图像，通过滤波去噪、角点检测等图像处理方法[14]，获得所有棋盘格边长的平均像素距离。每个棋盘格的实际边长是已知的，从而就可以获得每个像素表示的物理长度K，在测量时获得像素长度乘以K，就可以获得被测目标的物理长度。

图5 棋盘格

(2)

3.2 桨尖距离计算

桨尖距离的计算是根据上下旋翼的位置差量计算的，因此需要获得上下旋翼各自的位置。在系统工作时，通过外触发的方式获得旋翼旋转工况下的桨尖图像，如图6所示。图6中白色区域为桨尖截面，可见通过补光、调整曝光时间等措施获得的图像清晰，桨尖区域明亮，这为后续的图像处理提供了有利条件。

图6 桨尖原始图像

首先对原始图像采用灰度阈值分割，将图像转换为二值图，如图7所示，这样就可以将桨尖区域与背景分割[15-16]，然后通过边缘检测算法获得桨尖截面的轮廓，从而可以获得桨尖截面的封闭图形。为了使计算简便且提高计算速度，取桨尖截面的重心坐标作为桨尖的位置，如图8所示。

图7 二值图像

图8 桨尖位置检测

结合标定获得的坐标转换系数K和上下旋翼桨尖的像素坐标，可计算出上下旋翼之间的距离。计算上下旋翼桨尖之间的距离只关心垂向的距离，因此,设yup、ydown分别为上、下旋翼旋转时桨尖的垂向像素坐标，y0up、y0down分别为上、下旋翼静止时的垂向像素坐标。则上下旋翼的位移分别为

Dup=K(yup-y0up)

(3)

Ddown=K(ydown-y0down)

(4)

则上下旋翼桨尖距离为

ΔD=K(yup-ydown)

(5)

4 实验结果分析

本次实验采用4 m直径的共轴刚性双旋翼实验台，实验条件如表1所示。实验内容包括双旋翼悬停和双旋翼前飞两种状态。

4.1 桨尖位移测量重复性实验

在悬停状态下对系统的测量准确度和重复性进行实验，实验在转速896 r/min、总距角0°状态下进行。选取同一片桨叶在不同时刻的若干测量值对准度和重复性进行验证。选取上下桨尖距离的27次测量值考核准度，如图9所示，蓝色为桨尖距离实测值；绿色为桨尖设计理论值；红色为桨尖距离实测平均值。桨尖设计理论值为300 mm，实测平均值为299.3 mm，实测平均值与理论值相差0.7 mm，实测值的误差带为2.95 mm，实验结果表明，系统具有较高准确度，能够满足实验需求。

图9 桨尖距离准确度

选取同一片桨叶桨尖位移的27次测量值考核重复性，如图10所示，蓝色为下旋翼桨尖位移实测值，绿色为上旋翼桨尖位移实测值。下旋翼桨尖位移误差带为1.03 mm，上旋翼桨尖位移误差带为2.97 mm，实测值中的波动是由于旋翼在高速旋转过程中出现桨叶振动引起的，在实际应用中取多次测量的平均值，可减小测量误差。

图10 桨尖位移重复性

4.2 双旋翼悬停状态桨尖位移测量

双旋翼悬停状态桨尖位移测量，转速为896 r/min，通过操纵系统改变桨叶的总距角，获得了双旋翼桨尖位置随总距角的变化数据，由于4片桨叶在同一方位角的桨尖位移基本相同，图11和图12为桨叶的桨尖位移和间距的平均值。结果表明，上下旋翼桨尖位移随总距角的增大而增大，且上旋翼位移变化比下旋翼位移变化大，这是由于桨叶产生的升力随总距角增大而增大，桨尖位移也随之增大;同时,由于上下旋翼之间相互影响，上旋翼升力变化要大于下旋翼的升力变化，桨尖距离也随着总距角的增大而增大。当总距角大于8°以后，上下旋翼桨尖位置变化趋于同步，桨尖距离也基本保持不变，这也符合共轴双旋翼的气动规律[3]。

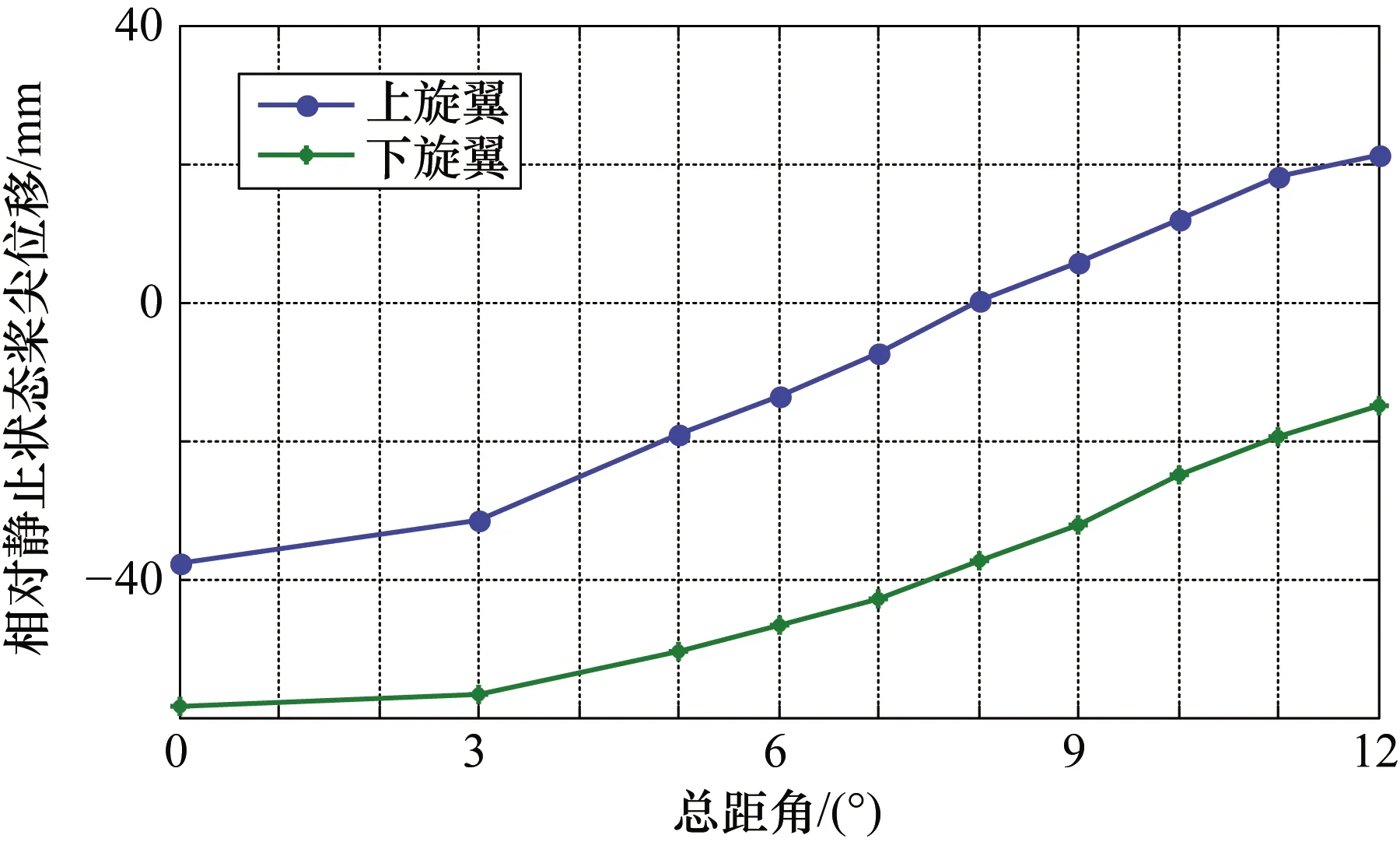
图11 相对静止状态桨尖位移

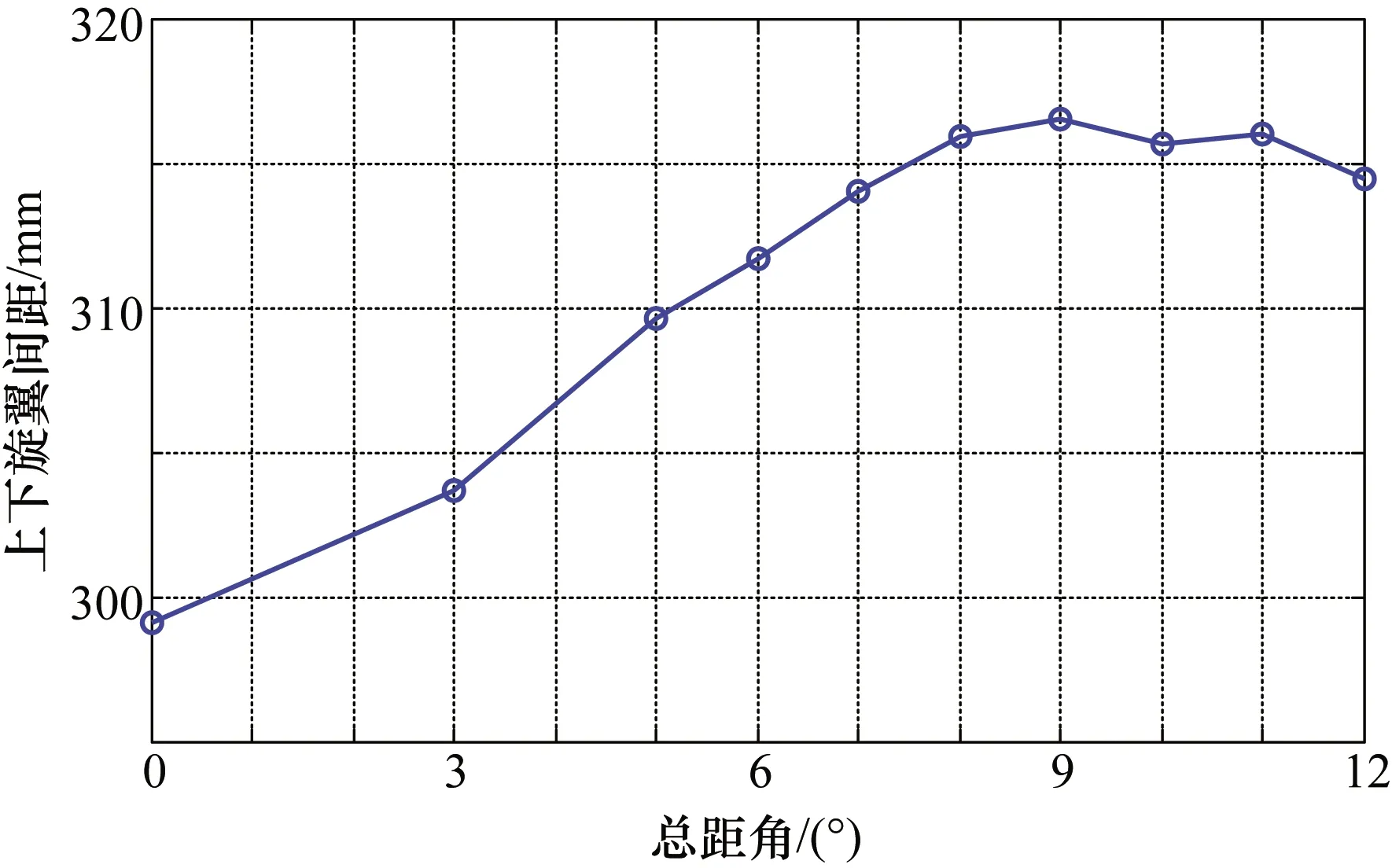
图12 上下旋翼桨尖距离

4.3 双旋翼前飞状态桨尖位移测量

双旋翼前飞状态时，影响桨尖距离的因素有升力偏置、前进比、交叉角、提前操纵角、旋翼气动干扰等，其中升力偏置是最重要和最显著的影响因素[3]。实验风速为28 m/s，旋翼转速447 r/min，前进比为0.3。图13给出了不同升力偏置和倾角状态的桨尖距离结果。

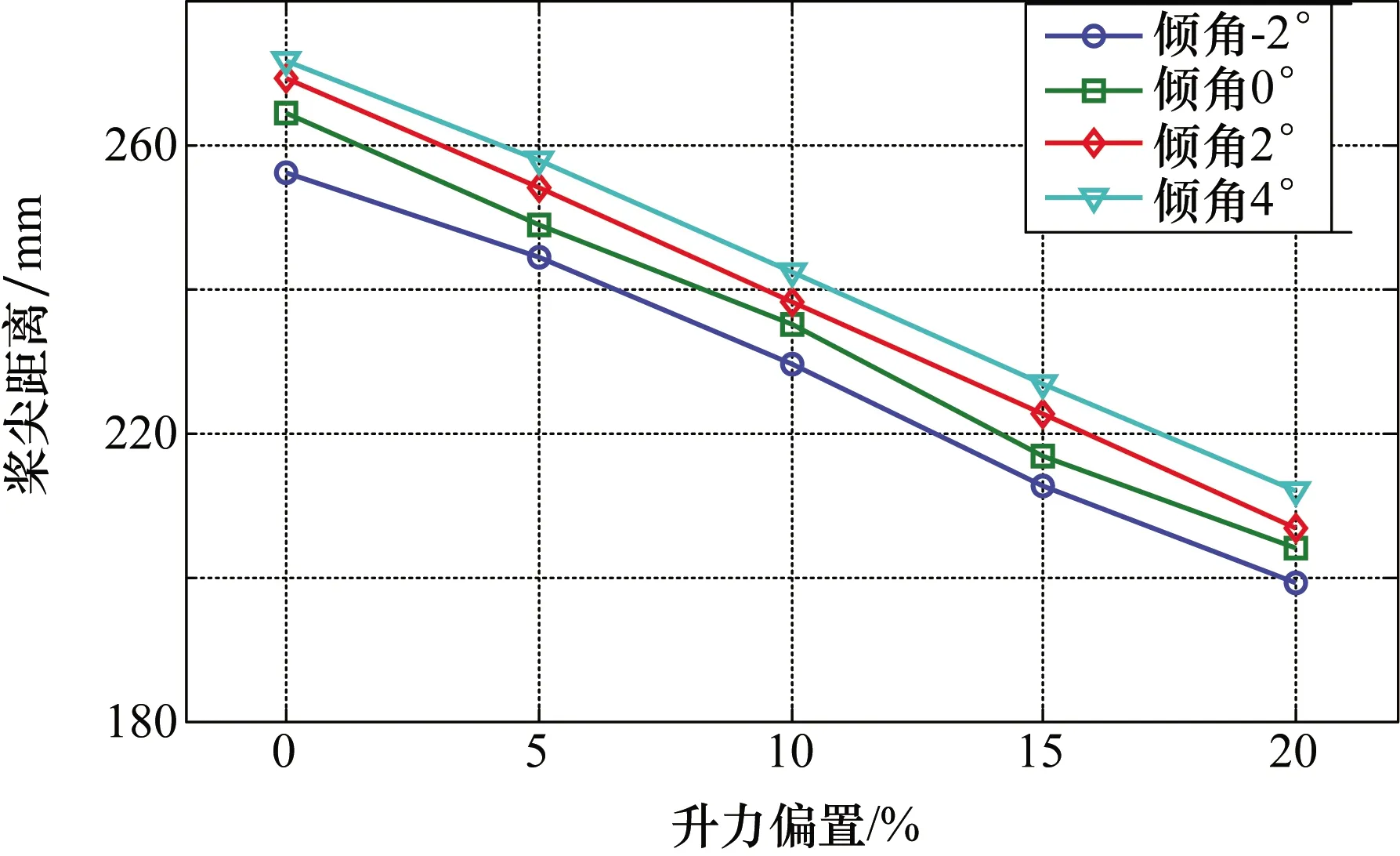
图13 不同升力偏置状态的桨尖距离

图13数据表明，上下旋翼桨尖距离随着升力偏置的增大而呈线性减小，在相同升力偏置条件下，随着倾角的增大而呈线性增大，数据符合共轴双旋翼空气动力学理论。

5 结束语

共轴双旋翼实验时，由于实验状态的不可预知性，上下旋翼桨叶有可能发生碰撞，造成实验模型和设备损坏，因此在实验时必须对上下旋翼桨尖距离实时测量与监测。笔者主要采用图像处理相关方法，提出了一种基于单目视觉的共轴双旋翼桨尖位移测量方法。根据实验条件和工况对硬件系统进行了详细设计，采用外部触发的图像采集方式，获取了清晰的桨尖图像。基于 Matlab软件平台开发了软件系统，采用测量标定、图像处理与识别等技术，完成了桨尖位移的测量。在4 m共轴旋翼实验中得到应用，获取了悬停及前飞状态的桨尖距离数据，数据符合共轴双旋翼空气动力学理论。结果表明该系统满足实验要求，并保证了实验的安全完成。