基于互信息与层次聚类双重特征选择的改进朴素贝叶斯算法

李欣倩，杨 哲，任 佳

(浙江理工大学 机械与自动控制学院，浙江 杭州 310018)

朴素贝叶斯(Naive Bayes)[1-2]结构简单、运算效率高，具有数学理论支撑，因此常用于解决二分类及多分类问题。在实际场景中，由于存在不确定因素，特征独立性假设往往难以达成，因此朴素贝叶斯算法虽然容易实现，却牺牲了部分分类性能。所以，研究人员从不同角度对算法进行了相应的改进。

一些学者从结构扩展的角度出发，提出了改进朴素贝叶斯算法结构的想法，不再视所有特征之间都相互独立，而是针对具体问题去寻找特征之间的相关性或部分相关性。Friedman等[3]提出了Tan模型，每个特征属性在类别变量的基础上，能够选择一个其他特征进行关联，其结构与树状图相似，又称树扩展朴素贝叶斯。

基于属性加权对朴素贝叶斯算法进行改进则提供了另一种思路，其赋予每个属性一个权值，权值的大小可由不同的方法确定，相较于前一种改进方法，该方法可以有效保留朴素贝叶斯算法原来的结构。Zhang等[4]提出了一种加权朴素贝叶斯算法，给出了Markov Monte Carlo法、爬山法、信息增益法以及相应的组合方法等5种选择属性的权值方法。魏会建[5]在结合粗糙集理论和信息论的基础上，提出了一种基于属性约简和属性加权的朴素贝叶斯算法，该方法能约简冗余属性，同时计算约简后的各条件属性相对于决策属性的权重，并融入到朴素贝叶斯算法中，从而达到改善算法应用场景和提高分类精确度的目的。

此外，一些学者从特征选择的角度出发进行改进研究，在原始数据集中删除无关或冗余的特征，用筛选后的特征子集进行算法的训练。特征选择是一种数据降维方法，其主要目的是在提高模型准确率或不降低准确率的前提下，尽可能地减少特征。常用的方法有Filter、Wrapper和Embedded。Filter方法使用某种距离或相似性度量准则计算特征和类别的相关性大小并进行排序，根据排序选择值最高的特征。Wrapper方法考虑了后续学习器的性能，并将其作为评价指标。相较于前者，其计算量虽有增大，但能获得更小、更优的特征子集。Embedded方法为一种嵌入式的特征选择方法，将特征选择嵌入于整个算法中，如ID3、C4.5、CART等一系列树类算法。为了改善使用信息增益进行属性选择时需要设定阈值的问题，Abellan和Castellano[6]提出了一种基于最大熵的快速属性选择方法，该方法使用不精确概率和最大熵准则来选择最具信息量的属性，且无须设定阈值。

最后，局部学习也是改进朴素贝叶斯算法的方法，通过改变训练数据的数量来改变模型的构造过程，使部分数据能满足特征独立性的要求。该方法在训练阶段选取一部分数据来构造分类器，这样可以有效降低整个数据集对特征属性独立性假设的限制。Frank等[7]提出了一种局部加权贝叶斯算法，通过学习局部模型来放宽独立性假设，对比其他的朴素贝叶斯算法，该方法计算简单，能够有效提高分类性能。

为了降低特征子集规模和提升分类性能，笔者提出了一种基于互信息与层次聚类双重特征选择的改进朴素贝叶斯算法。通过互信息方法剔除不相关特征，利用欧氏距离对特征进行层次聚类，之后从每个簇中选择信息量最大的特征并用粒子群优化(Particle Swarm Optimization,PSO)算法优化聚类簇的个数。在计算特征子集的先验概率和后验概率后，根据朴素贝叶斯算法得到特征所属类别。结果表明，该方法不仅能放宽特征属性独立性的假设，同时能提高分类的精准度。

1 朴素贝叶斯

朴素贝叶斯算法[1-2]为一种基于概率统计的分类方法，常作为文本分类的评估标准[8]。该算法在得到样本数据的先验概率与条件概率后，可根据贝叶斯公式求得后验概率，即样本对应不同类别的概率。后验概率最大的类别即为算法对应的样本预测类别，其中贝叶斯公式为

(1)

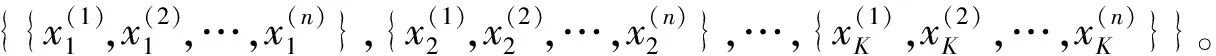
P(Y=cm)

(2)

P(X(1)=x(1),…,X(n)=x(n)|Y=cm)

(3)

(4)

该假设是指在输出类别确定的情况下，特征之间相互独立。该假设虽然存在降低算法分类准确率的情况，但是它能够简化模型、提高算法的可实现性。此时，模型计算公式为

(5)

因式(5)的分母对输出类别并无影响，故该算法仅需最大化式(5)的分子，即可确定样本所属类别，即

(6)

2 基于互信息与层次聚类双重特征选择的改进朴素贝叶斯算法

2.1 互信息

互信息(Mutual Information)[9]是一种度量信息量的方法，在给定随机变量X和Y后，互信息可以用于确定X中所含Y的信息量，或在X已知时Y所减少的不确定性。当X和Y均为离散的情况时，X的边缘分布为p(x)，Y的边缘分布为p(y)，两者之间的联合概率分布为p(x,y)。此时，X和Y之间的互信息为

(7)

当变量X和Y互信息为0时，表示X与Y相互独立，两者没有任何相关性。对比皮尔逊相关系数[10]，互信息系数衡量相关性的范围更广。所以，选择互信息来度量特征与类别之间的相关性强度。互信息值越大，表示该特征与类别之间的相关性越强，即包含的信息量越多。

2.2 基于欧氏层次聚类与互信息双重特征选择的改进朴素贝叶斯算法

层次聚类[11]，即树聚类，是一种高效的聚类算法[12]。层次聚类法根据簇与簇之间的相似度或者距离度量方式(如最大距离、欧氏距离、马哈拉比诺比斯距离)，构建一棵由簇与子簇组成的聚类树。重复此操作，并在符合停止条件时结束，如聚集到所设置的簇的个数。层次聚类算法包括凝聚法[13](Agglomerative)和分裂法[14](Divisive)，如图1所示。

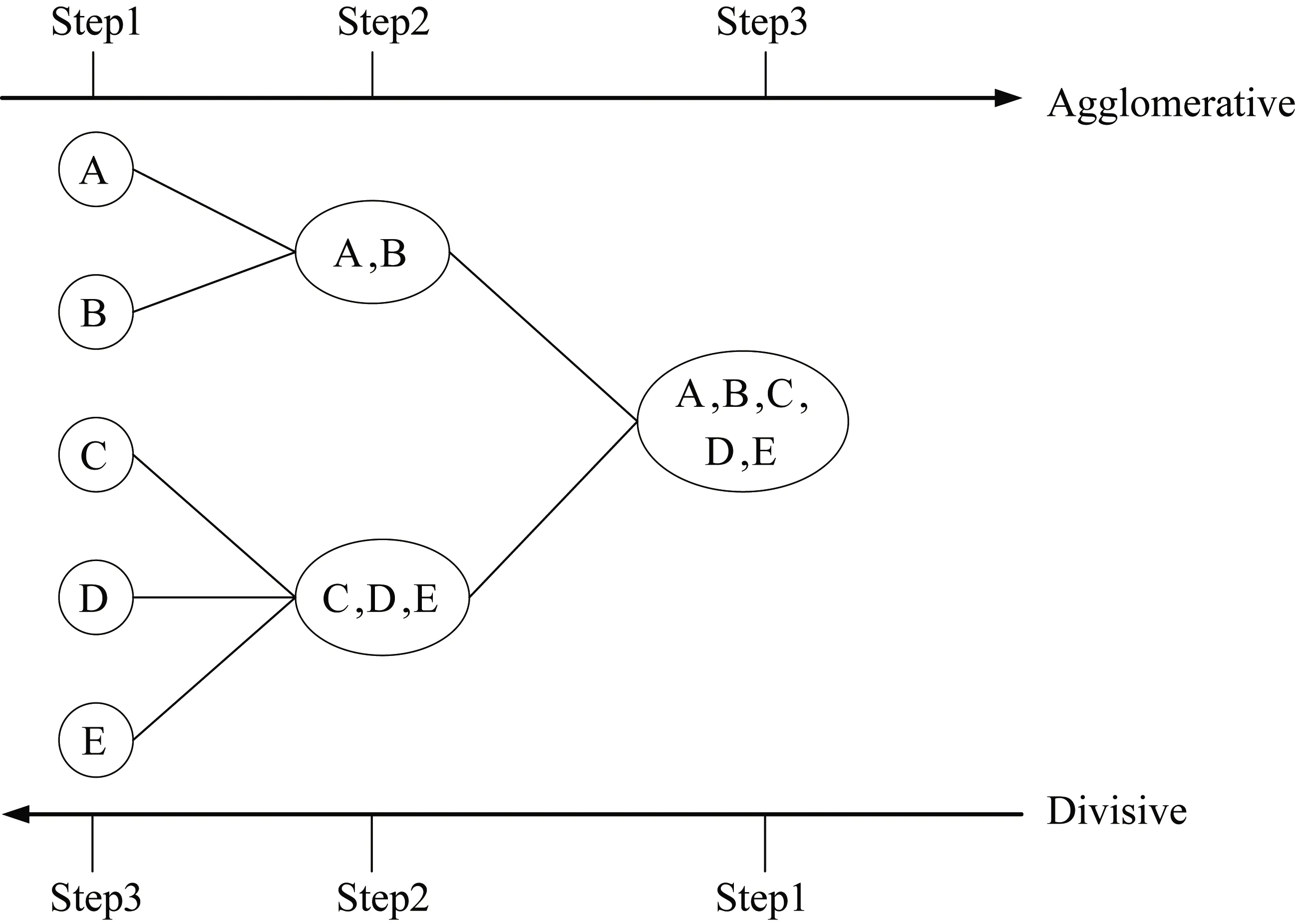
图1 层次聚类法示意图

在图1中，从左向右为凝聚法，该方法为一种由下而上的聚类方式，选定相似性或距离度量准则，将每个对象看作一个单独的簇,合并符合准则的簇，在满足停止条件或所有的簇聚为一类时合并结束。从右向左看即为分裂法，该方法在初始阶段将所有的对象处于同一簇中，再根据所选的度量准则，迭代分裂，符合停止条件或所有对象自成一簇时，结束分裂。

2.3 基于双重特征选择的改进朴素贝叶斯算法

朴素贝叶斯算法的假设在实际分类问题中较为严格且不易满足，所以将互信息与凝聚分层聚类方法结合，提出一种特征选择改进算法(MIHC_NB)，以便在采用朴素贝叶斯算法进行分类时，尽可能满足所需的假设条件，提升算法分类性能。MIHC_NB算法的框图和伪代码见图2、表1。

表1 MIHC_NB算法伪代码

图2 MIHC_NB算法框图

① 基于互信息算法的第一重特征选择。根据式(7)，得到所有特征对应不同类别的值，其中包含部分互信息值为0的特征。该部分特征不仅对算法性能的提升毫无帮助，而且还会增加模型的计算成本，因此剔除该部分特征。

② 基于凝聚层次聚类法的特征之间第二重特征选择。首先将每个特征(列向量)作为聚类对象进行转置，再根据欧氏距离，由下向上，将特征聚集成类。此处选用3种方式实现簇的合并，即最小离差平方和法(Ward-Linkage)、最远点法(Complete-Linkage)和平均距离法(Average-Linkage)。最小离差平方法首先计算两簇中所有对象距离两簇中心点的和，再合并距离最小的两个簇；最远点法则是合并最远点距离最小的两个簇；平均距离法在计算簇与簇之间所有对象距离的平均值后，合并值最小的两个簇。将特征聚集成簇的数量设置为Q，达到该设置时，迭代结束。

③ 计算Q个簇中所有特征和输出类别之间的互信息值，并将每个簇中数值最大的特征添加到所选的特征子集中，即所选的特征数量与聚类簇的个数Q相同。

④ 拆分数据集。采用留一交叉验证法评估特征子集的分类性能。每次取单个样本进行测试，将其他的样本用于训练。重复多次，直到所有样本经过测试后，使用平均值来衡量算法的分类准确率。该验证法能够降低个别噪声点造成的偏差影响，提高算法的鲁棒性。

⑤ 建立朴素贝叶斯算法的模型。根据式(1)～式(6)，依据上述步骤中得到的特征子集，建立朴素贝叶斯算法的模型。

⑥ 采用粒子群算法优化凝聚层次聚类法中簇的数量Q。因凝聚层次聚类法中簇的个数将直接影响所选特征的数量，所以本文选用粒子群算法[15]自动优化簇的选取数目Q，取值为[1,G]，以最优准确率Accuracymax作为优化目标。G为剔除步骤①中互信息为0的特征后余下的特征数量。在迭代次数达到Stepmax= 5000后，结束寻优过程，得到最优准确率Accuracymax及对应的最小特征数Featuremin。

3 实验结果与分析

3.1 数据集与实验环境

由表2可知，不同于传统数据集，医学数据集具有较多的特征，因此测试采用了6组高维医学数据集。表2中所用数据集能在www.gems-system.org.和ligarto.org/rdiaz/Papers/rfVS/randomForestVarSel.html上得到。前4个数据集均为二元分类问题，类别取值为0或1，用于检测是否患病。而后2组数据集则是多元类别，用来判别患者患病的程度(处于第几期)。在6组数据中，Prostate数据集所含样本数(102)和特征数(6033)最多。

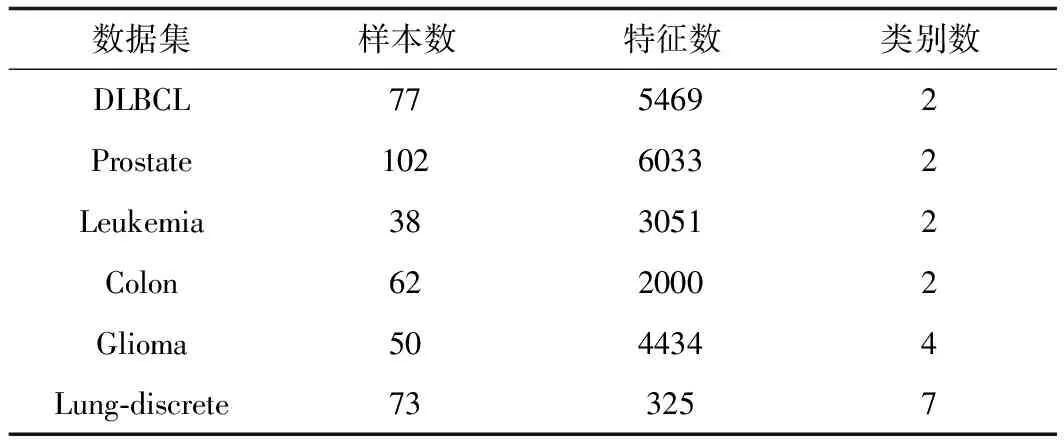
表2 实验数据

本实验的测试平台为Windows 10，算法实现为Python 3.6。

3.2 算法验证与分析

分层聚类算法由3种不同的欧式距离准则得到，因此本实验所用的双层特征选择算法有3种，即MIHC_NB-ward(基于互信息和最小离差平方和的分层聚类的朴素贝叶斯算法)、MIHC_NB-complete(基于互信息和最远点的分层聚类的朴素贝叶斯算法)和MIHC_NB-average(基于互信息和平均距离的分层聚类的朴素贝叶斯算法)。对比算法为MI ranking(基于互信息排序特征选择算法)，采用朴素贝叶斯算法衡量分类准确率，测试结果由留一交叉验证法得到。本实验与对比实验的最优准确率和最小特征数目如表3所示。

表3 实验算法在测试集上所得的分类性能对比

采用最大信息系数(Maximal Information Coefficient,MIC)[16]进一步验证本方法的性能。MIC与互信息[9]、皮尔逊相关系数[10]相同，也是一种度量特征间关联程度的方法，该方法在线性、非线性相关的情况中均适用。MIC将所得的互信息值进行了网格归一化处理，使互信息值分布于[0,1]范围内，能够增强相关性的可观程度。MIC数值越大，相关性就越强。通过MIC求得所选特征子集中两两特征间的相关性强度，并将结果相加后取均值。4种算法所得结果如表4所示。

表4 实验所得特征子集的平均MIC系数

由表4可知，在DLBCL和Colon数据集上，所提出的3种算法所得的MIC值均低于MI ranking算法，尤其是MIHC_NB-average算法得到的MIC值最小。该结果表明，改进算法不仅可以提高分类性能，而且能够有效减小特征的相关强度。虽然4种算法在Leukemia数据集上的分类性能相同，但提出的算法能够减小MIC值，尤其是MIHC_NB-average算法的MIC值相较于MI ranking算法降低了0.1807。在Prostate数据集上，改进算法同样可以达到减小特征间相关性的效果。在Glioma数据集上，3种算法的MIC值均低于MI ranking，且MIHC_NB-complete算法在3种评估方式中均取得最优的结果。在Lung-discrete数据集上，实验所得准确率虽然相同，但是3种改进算法均在一定程度上降低了相关性，尤其是MIHC_NB-average算法的MIC值仅为0.0765。最后，根据表4中数据及上述分析结果可知，MIHC_NB-average算法在除Glioma数据集外的5个数据集上特征间的相关性均为最低，为4种算法中最接近朴素贝叶斯算法假设的方法。由于特征与类别间的相关性也是影响算法分类性能的一个重要原因，所以单一的簇间聚类准则不一定会得到信息量最高的特征子集。所以对于不同数据集，选用的簇间聚类准则不同并采用粒子群算法优化聚类簇个数。

上述表3与表4中数据表明，采用基于互信息与层次聚类双重特征选择方法后可以明显降低特征之间的相关性，可见该方法作为朴素贝叶斯算法的前置算法，确实能够最大限度地满足其特征属性独立性假设，从而有效提高该算法的预测准确率。

4 结论与工作展望

为了进一步放宽朴素贝叶斯的假设，提出了一种基于互信息与层次聚类双重特征选择的改进朴素贝叶斯算法。该算法根据互信息方法剔除不相关特征，再利用凝聚层次聚类法将相关性强的特征进行聚类，最后将每簇之中互信息值最大的特征合并为最终的特征子集，尽可能地消除特征间的相关性。实验结果表明，所提出的算法可以减少特征间的相关性强度，并且优化特征选取、提升分类性能。同时，更快地确定聚类簇的个数、加快优化算法的速度是下一步的主要研究内容。