基于落锤装置的体积弹性模量测定方法

徐春冬，施宇成，商 飞

(南京理工大学 机械工程学院，江苏 南京 210094)

液压介质的压缩性是分析液压系统性能必须考虑的因素之一[1-4]，通常用压缩率k来表征，其物理含义为压力增加一个单位时的体积相对变化率。

(1)

式中：ΔV为体积改变量；P为压力；V0和P0分别为初始体积和压力；负号用于使k取正值。压缩率的倒数称为体积弹性模量(也叫容变弹性模量)，记作K。

常见的液压传动系统和控制系统的工作压力都在50 MPa以下，这时，可认为体积弹性模量是常数，不随压力变化。但是对于某些在超高压状态下运行的液压系统，体积弹性模量为常数的假设将造成理论预测的失准，落锤液压发生器就是一个典型例子。市川常雄[5]在其专著中也曾提到，K随压力增大而增大，但是没有给出定量的数据。文献[6]介绍了几种测定液体压缩性的典型方法，并给出了甘油在0.1～1200 MPa压力作用下的体积弹性模量变化。文献[7]对体积弹性模量重新定义，使计算结果可以匹配测试数据，但该方法仅通过了气体介质验证，对液压介质的适应性有待考察，且没有明确的适用压力范围。基于物态方程可以求解固体材料的体积弹性模量变化规律[8-9]，这种方法对液压介质的有效性还需论证。

国内外关于液压介质体积弹性模量尚未建立起标准的评价方法和测定设备，主要的测量原理是根据体积弹性模量的定义，测定特定体积变化量下的压力变化求取[10-11]。根据定义，目前液压介质体积弹性模量的测定方法分为等温法和等熵法。其中，等温法最为常用，是在恒温条件下测定的，测得的是等温体积弹性模量，亦称静态体积模量，适用于压力和体积变化非常缓慢、热交换保持恒定的系统，这与美国MIL-PRF-83282D规范一致；等熵法则用于动态过程的体积弹性模量测定，测得的是动态体积模量，适用于交变压力下的液压系统。目前现有的测定方法适用的压力测定范围往往不是很高，且测量系统较为复杂，步骤烦琐，不适用于液压介质体积弹性模量的快速动态测量。

本文通过落锤液压标定装置，深入探讨常量体积弹性模量在超高压状态下的不适用性，在此基础上构建体积弹性模量的测定方法，并通过比对试验结果验证了测定方法的可行性。

1 落锤标定装置工作原理分析

落锤标定装置的工作原理如图1所示。沿导向系统自由下落的重锤与油缸顶端的精密活塞相撞，通过活塞压缩油缸内的液压油在油缸内产生压力。当落锤的动能全部转化为液压油的弹性势能时，重锤与活塞达到最大压缩行程，油缸内的压力达到最大，其后由于液压油的弹性恢复作用，把活塞与重锤上推，直到重锤跳离活塞，弹性势能又转化为重锤势能。这样在油缸内形成一个近似于半正弦的压力脉冲，该正弦脉冲能够模拟大多数武器的膛压曲线，因此落锤标定装置常用于进行塑性测压元件的准动态校准、传感器比对式校准和传感器准静态绝对校准[12-14]。

图1 落锤标定装置示意图

假定质量M的重锤从h高处下落，冲击初始容积V0的油缸顶部截面积为S的活塞，压缩油缸内的液压油，产生压力脉冲P。通常认为体积弹性模量是常数(记作K0)，意味着可以把油缸内的液压油看成一根等刚度的液体弹簧[15]。由于整个过程时间极短，可看作完成非弹性碰撞过程，即假设运动期间重锤与活塞杆未分离，并一起运动向下位移x，重锤和活塞杆可看作一个整体，且活塞杆质量相对重锤极小，可忽略，由机械结构造成的阻力记为F0，根据上述条件可得落锤向下运动时的物理模型如下。

① 运动方程：

(2)

② 协调方程：

ΔV=-Sx

(3)

③ 物理方程：

(4)

(5)

将式(5)代入式(2)，可得

(6)

运动初始条件为(视锤体为自由下落)

(7)

通过常微分方程求解，解得

(8)

将式(8)代入式(5)，可得压力峰值Pm为

(9)

由于超高压实际运动过程中重力Mg和阻力F0相对于压力的数量级差异极大，可忽略运动中的重力和阻力，最终反映落锤标定波形的特征值用峰值Pm和脉宽τ描述，如图2所示，其数学形式为

图2 油缸内的压力脉冲

(10)

(11)

由式(10)和式(11)，通过选取合适的落锤质量组件、造压油缸的初始容积、精密活塞组件的有效面积，可以获得对应的半正弦压力峰值和脉宽。

2 常量体积弹性模量存在的问题

为说明体积弹性模量默认设定为常量时存在的误差问题，组建图3所示的落锤标定系统，以实际的工程标定数据解析超高压下默认体积弹性模量为常数的缺陷。试验在常温条件下进行，以避免温度对测量结果引入干扰，液压介质采用常用的蓖麻油，标准传感器采用Kistler 高精度6213B压电传感器，从而确保测试结果的准确性。

图3 超高压落锤液压标定试验系统

如表1所列，Pml、τl为根据式(10)和式(11)求出的压力峰值、脉宽预测值，Pms、τs为工程标定的实测峰值和脉宽值，落锤标定装置运行参量设定为：M=6.13 kg，V0= 3.86 cm3，S= 1.0 cm2，液压油采用蓖麻油，K0= 2.10×109Pa。由表1数据可知，实测值和理论预测值之间存在明显的差异：实测的压力峰值Pms大于理论预测值Pml，且差异随落高的增加而增大，实测的脉宽τs小于理论预测值τl，且随落高的增加而减小。而由式(11)可知，理论预测的脉宽值应与落高无关。

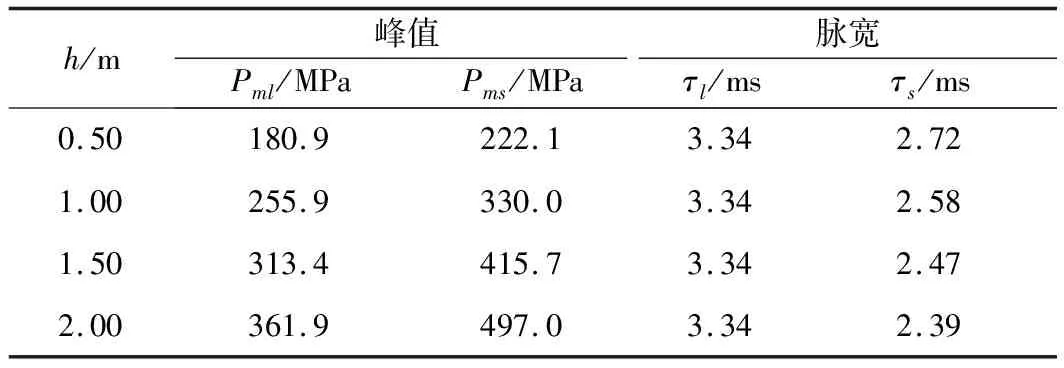
表1 理论值与实测值的比较

用幂函数拟合表1中的{hi，Pmsi}数据，得

Pms=331h0.58

(12)

式中：h的幂指数大于0.5，而根据式(10)预测Pm应与h的0.5次幂成正比。分析式(10)中各个参量，M、V0和S是落锤标定装置的结构参数，都是可以准确测量的定值，与h无关，只能是体积弹性模量含有与h有关的因素：落锤初始高度h，必然是相对压缩量ΔV/V(可以说是压力P)的函数，因此油缸内的液压油的物理模型应当修正为一根变刚度的液体弹簧，即一根在压缩过程中逐渐变“硬”的弹簧。根据以上分析，落锤初始高度增加时压力峰值比预期大、脉宽比预期小的现象就得到了合理的解释。为获得准确的动态体积模量，需寻找模量相对于压力的修正模型。

3 体积弹性模量动态测定方法

实验测得的落锤标定装置的压力峰值“异常”表明，压力峰值中含有液压油的体积弹性模量随压缩量变化的信息。换个角度思考问题，可以把落锤标定装置用作实验设施，构建测定液压油体积弹性模量变化规律的实验方案。这是相反相成的辩证思维的必然逻辑结果。

通过对实验数据的分析，假设体积弹性模量与相对压缩量之间存在线性关系，表示为

(13)

式中：β为修正系数，且有

ΔV=Sx

(14)

故

(15)

式中：V0为油缸初容积;S为活塞截面积;x为冲击后的重锤(活塞)位移。经整理，得

(16)

式中：xm为活塞最大位移。

根据组合测量原理，设定若干个落高hi，测定落锤标定装置在各个运行状态下的{Pmi，xmi}如表2所列，落锤标定装置工作参量设定为：M= 6.13 kg，V0= 3.86 cm3，S= 1.0 cm2)，将它们代入式(16)，得到一组超定方程组，应用最小二乘法，便可得出K0和β的测量值。

其中压力值通过标准传感器感受缸内压力测得，位移值只需要在精密活塞侧壁安装激光位移传感器即可获得。

按上述思路处理表2的实验数据，得到

表2 测量蓖麻油体积弹性模量的实验数据

K0=2.24×109Pa，β=8.36×109Pa

按照文献[6]的分类，上述实验方案测得的是绝热平均体积弹性模量，属于等熵法的测定方法。

4 方法有效性验证实验

为了验证所推导出的液压油体积弹性模量变化规律的有效性，将模型公式反代入压力峰值、脉宽求取公式，得到相应的理论预测值，并与实际测量值进行比较，试验条件与第2节相符。

考虑落锤标定装置落锤冲击活塞后的运动过程，根据机械能守恒定律，可得：

(17)

(18)

可得:

(19)

(20)

用式(10)进行迭代计算得xm值，再代入式(15)和式(20)，便可计算出峰值和脉宽的理论预测值。

选择工作参数M=23.04 kg，V0=3.56 cm3，S=1.0 cm2组织验证实验，结果如表3所示。

表3 验证实验的结果

数据表明，在测定液压油压缩特性的压力范围内(500 MPa以内)，预测准确度在2.0%以内；在压力外推2.5%的范围内，预报准确度在3.5%以内。因此，与文献[6]中介绍的测量液压油压缩性的方法相比，本文提出的基于动态测量的方法具有实验周期短、操作方便的特点，且测量结果的准确度可以满足工程应用的要求。

5 结论

① 通过分析落锤装置的运动特性，获得常量体积弹性模量下压力信号的特征参数理论公式，通过与实际测量值比较，得出在超高压状态下使用常量体积弹性模量计算的压力信号与实际严重不符，证明体积弹性模量在超高压下发生了较大变化。

② 提出体积弹性模量动态测定方法，对常量体积弹性模量进行了修正。

③ 通过落锤装置进行验证试验，获得数据表明在测定液压油压缩特性的压力范围内(500 MPa以内)，预测准确度在2.0%以内；在压力外推2.5%的范围内，预报准确度在3.5%以内，证实了液压介质弹性模量测定的有效性。

④ 使用该方法测定液压介质的体积弹性模量，对落锤装置的加工精度，尤其是造压油缸的加工精度，有严格的要求，且不适用于小压力下的液压介质体积弹性模量的修正。