“图形与几何”课程内容探析

刘久成

【摘 要】小学数学课程内容“图形与几何”历来是课程改革争论的焦点之一。基于现实需要，以及数学学科和小学生认知的特点，我们认为，小学图形与几何课程内容的确定应关注以下几个问题：学校教育的早期，教学欧氏几何是重要的，但应适当拓展几何课程内容领域;几何属性的数量表示值得关注，并凸显其直观性;内容呈现要重视情境设置和问题探索，体现从生活到数学、由直观到抽象的特点，并保持数学教材内容一定的逻辑严谨性。

【关键词】小学数学 图形与几何 课程内容

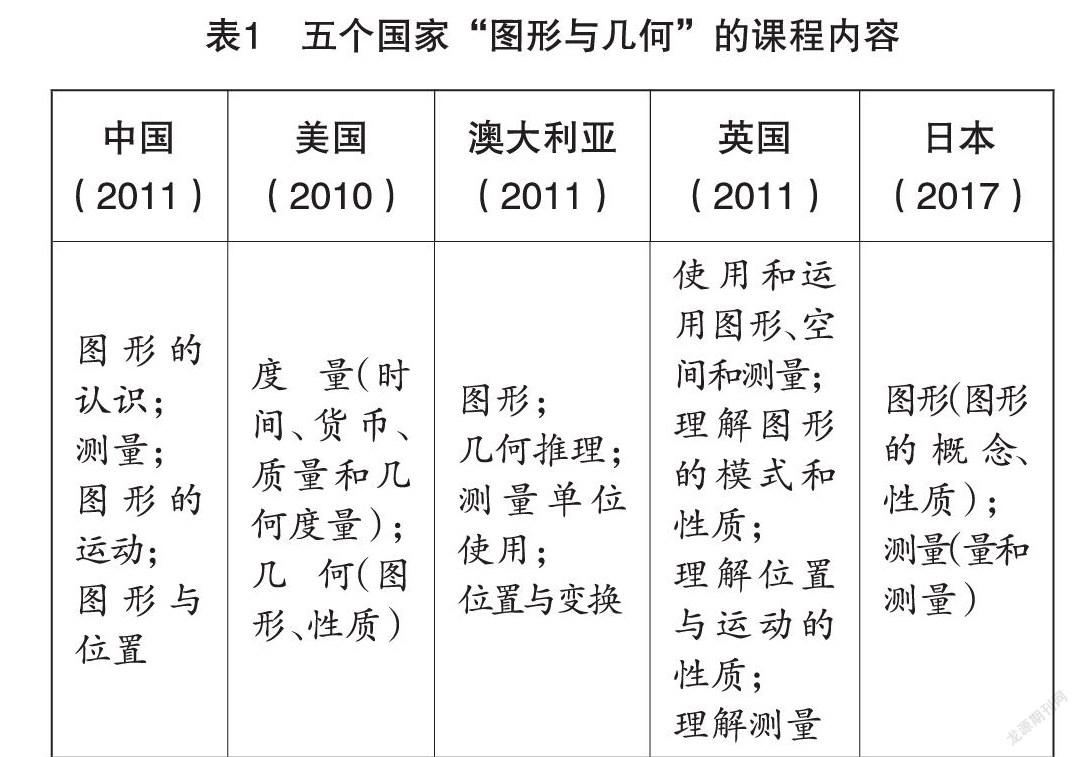
苏联学者斯托利亚尔曾说，不确定“教什么”的问题，就不可能解决“如何教”的问题。因此，“教什么”相对于“怎么教”来说是前提，如果教学内容本身出了问题，那么再好的方法手段也无济于事。几何学是研究“形”的分支学科。几何学的发展，让人们看到了几何的多样性，也让人们感受到，数学既有发现的特征，也有发明的特征。“图形与几何”是小学数学课程内容之一，是几何学最基础的部分，其课程内容改革一直是争论的焦点之一。从表1中我们可以看到，中、美、澳、英、日五国现行课标中关于图形与几何的课程内容显示出明显的差异。

比较发现，各国图形与几何的教学内容都有了拓广，不再严守欧氏几何概念体系，一般都涉及图形的认识、测量、变换与位置。通过具体比较可以发现，图形与几何内容大多集中在对简单二维和三维图形特征的认识上，但在内容广度和深度设置上有一定的区别。

20世纪70年代，斯托利亚尔在谈到数学教育现代化时曾指出，几何教学问题是数学教育现代化最复杂的问题之一，它引起了广泛的、世界性的争论。直到今天，图形与几何课程内容仍然是数学课程中最不统一的一个部分。同时我们看到，新课改以来，对于图形与几何课程内容的确定鲜有成果可以借鉴分析。由此，笔者基于现实需要，以及数学学科和小学生认知的特点，提出小学图形与几何课程内容的确定应关注的几个问题。

一、学校教育的早期，教学欧氏几何是重要的，应该鼓励学生去研究简单的几何图形，并探索这些图形的性质

欧氏几何诞生两千多年来，一直被视为学习几何知识和培养学生逻辑思维的典范。20世纪60年代，曾有人建议中小学数学不再保留欧氏几何体系。但时至今日，人们仍然认为，欧氏几何建立了一种最简单、最直观、最能为学生所接受的数学模型，是理解、描述和联系现实空间的工具，让学生利用这样的模型去思考、去探索，可以使学生体验到数学推理的力量。数学大师陈省身先生也指出：“一定要讲欧氏几何，从前欧几里得几何是整个教育的一部分，而不仅仅是数学的一部分。因为通过它可以使学生在简单的情况下获得一些推理。”欧氏几何的直观性、难度的层次性、真假的实验性，以及推理过程的可预见性，使它成为训练逻辑思维和演绎推理的理想材料和工具。同时，我们看到，欧氏几何的概念、性质和相关测量在实际生活和生产实践中有着极为广泛的应用，有助于学生感受数学的价值，激发学生对数学的兴趣。当然，在低年级，接近欧氏几何的方式必须是非形式的和解释性的，而系统化则留给较高年级。

二、小学图形与几何学习领域应适当拓展，更多地联系生活实际，向学生展示图形与几何在生活实践中的应用，并讓学生感受到这些应用会影响他们的生活

自20世纪贝利—克莱因运动以来，人们开始重视实验几何、直观几何，将运动思想引入几何。我国进行的本次课程改革也强调几何变换，让图形“动起来”，在运动和变换中研究和揭示图形的性质，虽未明确给出这些图形变换的定义，但相关内容已超出了欧氏几何的概念体系。“图形的运动”在小学阶段主要有两种情况：一是形状和大小不变，只是位置发生变化（合同运动），包括轴对称、平移、旋转;二是形状不变，大小变化（相似运动），如放大、缩小。本次课改之前，小学数学只涉及轴对称图形，不包含图形的平移、旋转和放大、缩小，现列入这些内容至少有以下几点理由：

一是解决实际问题的需要。弗赖登塔尔指出，数学的根源是常识，人们通过自己的实践，把这些常识通过反思组织起来，不断地进行系统化。现实世界中，轴对称、平移、旋转的现象大量存在，观察和认识这些现象，有助于人们用数学的眼光观察世界，用数学的思维思考世界，用数学的语言表达世界，提高认识世界的能力。

二是欧氏几何公理体系的建立，使它与逻辑推理结下了不解之缘，现在看来，逻辑推理也并非“欧氏几何”所独有。况且，除了发展学生的逻辑推理能力，还要发展其合情推理能力，以及观察、操作、实验、探究等方面的能力。因此在国际范围内，传统意义上的欧氏几何概念体系有逐渐被打破的趋势，多样化几何进入中小学课程已成为现实。图形的运动隶属于变换几何，写进义务教育数学课程标准，使得几何学习领域得到了拓展，也使小学几何课程的内容更为丰富。

三是“图形的运动”在于考查图形在运动下的不变性特征。这种数学思想方法非常重要。1872年，著名德国数学家、埃尔朗根大学教授菲利克斯·克莱茵提出的几何学新定义，就是把几何定义为一个变换群之下的不变性质，并且引出了按照变换群对几何进行分类的思想。

四是轴对称、平移、旋转的内容更具有现实性和操作性，其概念和性质为图案的设计、图形面积的计算，以及认识复杂图形和全等图形等奠定基础。这些问题并非来自欧氏几何，也无须要求学生了解相应几何领域的概念系统，但它对于提高学生研究图形的兴趣、提升学生的几何直观能力、发展学生的空间观念和推理能力都很有帮助。

三、在小学，几何属性的数量表示是值得关注的领域

我们已经看到，用代数的方法研究几何具有重要的教育价值。17世纪法国数学家笛卡尔做了开创性工作，建立了解析几何学。现行中学教材中引进向量几何的做法，也有助于几何与代数的融合。因此，在小学适当渗透坐标思想，用数对或者方向与距离来表示位置，是空间位置的量化手段，不仅易于学生理解，也有利于中小学的衔接。同时坐标几何知识的运用，也体现了数形结合的思想。

四、历史地看，几何课程内容有如下几个特征：直观的、计算的、概念的、代数的、功利的、实用的，在制定小学数学课程内容时必须做出选择

我们看到，我国小学几何在20世纪50年代强调计算（求积），70年代注重功利和实用，80年代至90年代直观与计算并重，现行图形与几何课程内容应该更具综合性，体现其直观、计算和应用的特点。内容呈现重视情境设置和问题探索，体现从生活到数学、由直观到抽象的特点。这就要求我们处理好不同情境类型的比重，特别是生活情境和数学学科情境的配合。过多的生活情境可能出现“去数学化”的倾向，数学自身的情境过多也会出现“去生活化”的倾向。小学生学习图形与几何，不是以公理体系为基础而是以生活经验为基础进行的，儿童通过折叠、搭建、摆拼等操作活动，来积累表象，丰富经验，加深对图形特征的理解。根据皮亚杰的研究，让学生用尺规动手画图，可以促进学生对几何概念的理解，感悟图形的存在。

比如，过两点画线段，可以让学生感受线段的特征：直的、有两个端点、可测量长度。

又如，过直线外一点，画已知直线的平行线、垂线、垂线段，可以促进学生感悟平行公理、垂线的唯一性、垂线段最短等性质。

五、小学几何课程内容既要根植于儿童实际，又要言之有据，形成循序渐进、互相连接的逻辑框架

学生学习图形与几何的基础是生活经验，不可能跳过早期的直觉阶段对几何事实、概念进行全面的理解。课程内容的设计应采取螺旋上升的方式，在不同水平上对同一课题进行教学。现行教材一般是让学生先直观认识简单的几何形体和常见的平面图形，然后再进行一维、二维、三维图形的进一步认识。这样循环交替、螺旋上升式的内容设计，既考虑到数学知识的系统性，又兼顾了学生的认知特点。

学习心理学研究表明：学生学习几何，先有具体概念，再有定义概念。如认识长方形和正方形，一年级先直观认识，此时学生只有具体概念，对图像的识别建立在经验中的“形状参照”。如像“门”一样形状的图形就是长方形，像“地磚”一样形状的图形就是正方形。学生在低年级对这些图形仅仅是通过直观的感知来积累表象，并且通过整体辨认作出判断，既不分析它们的特征，更谈不上去研究它们的各个要素和逻辑联系，到中年级时才逐步建立抽象概念，揭示它们的特征与关系。

再如，线段、射线、直线的教学内容安排。1978年到新课改之前，都是在低年级先教学直线、线段，到中年级讲“角”之前再引出射线，完成直线、线段、射线的教学。

这种做法，符合欧氏几何概念体系，但容易出现一个问题：直线的无限延伸性往往被学生忽视，或者学生虽然记住了这一点，但对它缺乏深刻领悟和具体感受。事实上，“直线”概念有三个要素：直、无粗细可言和无限延伸性。其中，“直”和“无粗细可言”可以通过直观教学并且运用同一性抽象得出。如“直”可以通过教具演示、通过与“曲”的对比，使学生认识。“无粗细可言”也可以借助典型事例的观察和分析让学生认识到。如教室墙面的浅色区域和深色区域的分界线、折纸折出来的折痕等都是没有粗细的线的例子。但“无限延伸性”难以通过直观教学使学生获得。因为我们找不到这样的实际事例，“无限长的直观教具”我们是拿不出来的。能拿出来的，只能是“有限的”。于是，这种无限延伸性只能由教师告诉学生，由学生发挥想象力。现行教材调整了教学顺序，在低年级配合长度单位的教学先认识线段，因为量长度本质上是量线段的长度，从逻辑上说，应该先有“线段”概念，到中年级讲“角”的时候再引出射线、直线。这样由具体到抽象，从有限到无限，既具有一定的逻辑性，又符合儿童的认知特点。

注：本文系全国教育科学规划教育部重点项目“改革开放以来小学数学教科书内容嬗变及其经验研究”（编号：DHA190371）的研究成果。