合理转化数与形，让解题更加高效

蒲毅

华罗庚教授曾说：“数缺形，少直观;形缺数，难入微.”将数形结合起来，合理进行数与形之间的转化，将几何图形中的位置关系、图形的性质用数量关系表示出来，或把数量关系用图形呈现出来，能有效地提升解题的效率.下面结合实例来谈一谈数形结合思想在解题中的应用.

一、数形结合思想在解答集合问题中的应用

集合中的元素可用数轴、坐标轴上的点表示，因此在解答集合问题时，可借助数轴、直角坐标系来解题.集合中的元素、集合之间的关系可用Venn 图来表

示，因此也可通过分析Venn 图来解答集合问题.

例1.已知集合，则 M ⋂N 为（  ）.

A.或3<x ≤7

B.或3≤ x <7

C.或x >3

D.或x ≥3

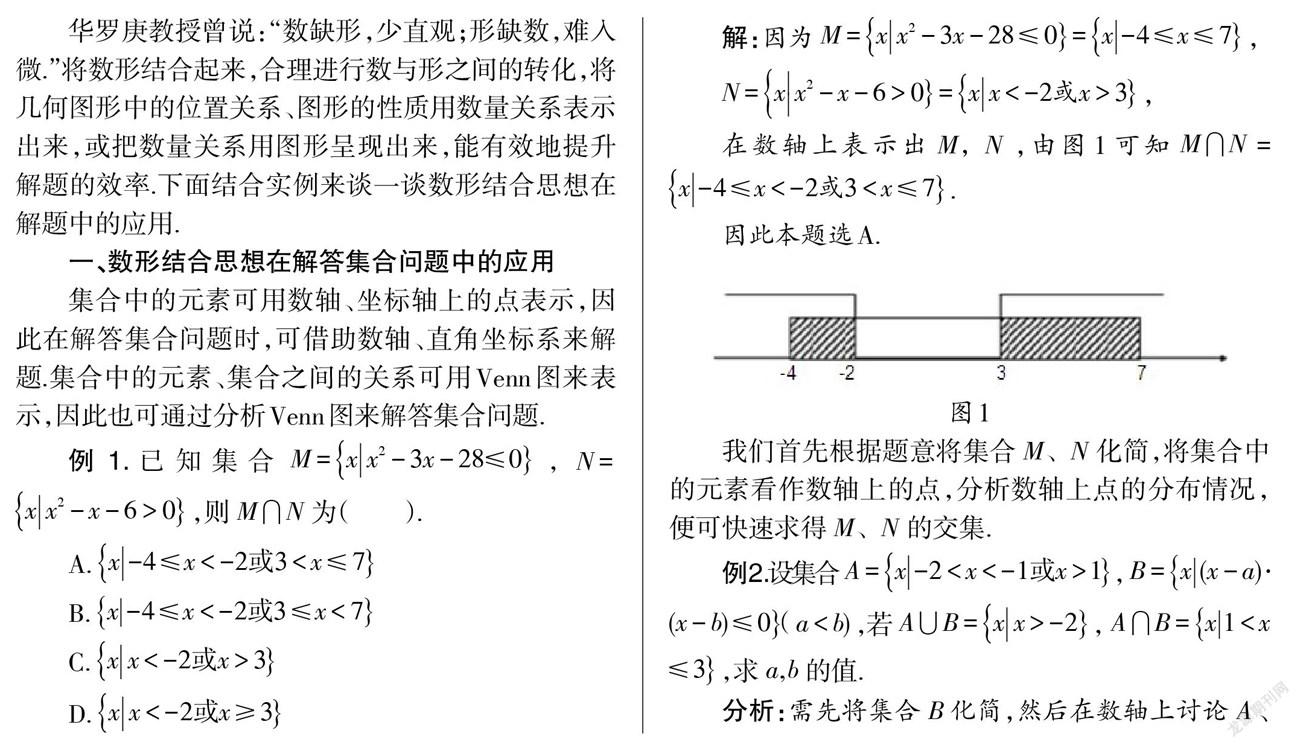
解：因为， 或x >3，

在数轴上表示出 M， N ，由图1可知.

因此本题选A.

我们首先根据题意将集合 M、 N 化简，将集合中的元素看作数轴上的点，分析数轴上点的分布情况，便可快速求得 M、 N 的交集.

例2.设集合或x >1，B =x（x -a）⋅（x -b）≤0（a <b），若 A ⋃B =xx >-2，A ⋂B =x1<x ≤3，求 a，b 的值.

分析：需先将集合 B 化简，然后在数轴上讨论 A 、B 的交集和并集.由 A⋃B =xx >-2知 B 的两个端点落在 E 的右侧，由 A⋂B =x1<x ≤3可知 B 的右

端点 H 必落在3的位置上.若左端点落在 F 的左侧，则与 A ⋂B 矛盾;若落在 G 、H 中间，则与 A ⋂B 矛盾;若落在 F 、G 之间，则与 A ⋃B 矛盾，因此当且仅当左端点落在 F 处满足题意，由此便可求得a 、b 的值.

解： B =x（x -a）（x - b）≤0=xa ≤ x ≤ b，

因为 A ⋂B =x1<x ≤3，在数轴上表示出 A 及B，如图2所示.

若 A ⋃B =xx >-2，则-2<a ≤-1，b≥1;若 A ⋂B =x1<x ≤3，则-1≤ a ≤1，b =3.

综上可得：a =-1，b =3.

二、数形结合思想在解答函数问题中的应用

函数图象是函数的一种表示方法，因此在解答函数问题时，同学们要学会将函数的解析式与函数的图象结合起来，运用数形结合思想来解题.可根据函数的解析式画出函数的图象，分析某个区间段上的函数图象，以明确区间上的端点值、最值、单调性、对称性;也可根据函数图象上确定的点的坐标，求得函数的解析式、零点，明确函数的性质.

例3.求函数y = x2-3x +2的定义域.

解：要使函数有意义，需使x（x）2 x，+2≥0，

画出 y =x2-3x +2的图象，如图3所示.

由图可知要使x2-3x +2≥0，需使 x ≤1或x ≥2，而 x ≠0，所以函数的定义域为：-∞，0⋃0，1⋃2，+∞.图3

本题主要考查了函数的定义域.可根据整式的性质：根号下的式子不小于0、分母不为0来建立关系式，然后结合二次函数的图象分析两个关系式的解的情况，从而求得函数的定义域.

例4.求函数 y =x2-2x -3，x ∈-1，2的值域.

分析：该函数为二次函数，根据函数的解析式画出函数的图象，如图4所示.在图4中找到x 取-1、2时的点，便可明确函数在-1，2上的变化趋势，确定最低点和最高点，便可求得函数的最值.图4

解：画出如图4所示的函数图象，其中浅色部分为函数在定义域-1，2上的图象，由图可知，函数的最大值在 x =-1处取得，函数的最小值在对称轴处取得，当 x =-1时，y =0;当 x =1时，y =-4，所以函数的值域为0，-4.

三、数形结合思想在解答解析几何问题中的应用解析几何中的每个曲线都有其对应的方程，如椭圆的方程为x2+y2=1（a >b >0）;双曲线的方程为 x2-=1;抛物线的方程为 y2=2px（p >0）;等等.在解答解析几何问题时，可根据圆锥曲线的方程画出相应的图形，通过讨论图形中的点、直线、曲線的位置关系求得问题的答案，也可根据图形中曲线的特征构造相应的方程，通过运算、推理求得问题的答案.

例5.若圆x2+y2-4x -4y -10=0上至少有三个不同的点到直线 l：ax +by =0的距离为2 ，则直线l 的倾斜角的取值范围是（  ）.

A.ππB.π5πC.ππD.0，π

解： x2+y2-4x -4y -10=x -22+y -22=18，则该圆是以2，2为圆心，3为半径的圆，

而ax +by =0是一条过原点的直线，设直线的方程为：y =kx，

由点到直线的距离可得2k -22=2，解得 k =

由图5易得为 .因此本题选B.

解答本题，需根据图形明确直线与圆的位置及其关系，讨论直线可能在的位置，然后根据点到直线的距离公式以及直线的倾斜角公式求得斜率以及倾斜角的范围.

例6.已知 P 为双曲线 x2-y2=1的右支上一点，M ， N 分别是圆x +52+y2=4和x -52+y2=1上的点，求PM -PN 的最大值.

解：由 x2-y2=1知 a =3，b =4 ，焦点为±5，0，

由x +52+y2=4和x -52+y2=1知两个圆的半径分别为 R1=2，R2=1.

由图6易知，PM max =PF1+R1=PF1+2，;

所以PM -PN max =PM max -PN min =（PF1+2）-（PF2-1）=PF1-PF2+3;

因为 P 在双曲线 x2+y2=1的右支上;

所以PF1-PF2=2a =6 ，

所以PM -PN max =9.

結合图形找出相应的点、直线、曲线的位置及其关系，便能快速建立起它们之间的联系，构建出关系式，使问题得解.

四、数形结合思想在解答不等式问题中的应用

在平面直角坐标系中，不等式 ax +by +c >（<）0表示的是直线左侧或者右侧的平面区域;若方程ax2+bx +c =0（a >0）的两个根为 x1， x2（x1<x2），则不等式 ax + by +c >0的解集为xx<x1或x >x2，不等式 ax+ by +c <0的解集为xx1<x <x2，由二次函数y =ax2+bx+c 图象可知其解集的分布情况如图7.在解答不等式问题时，可根据不等式画出相应的直线、二次曲线，借助图形来分析问题，这样能将抽象的问题直观化，达到化难为易的目的.

例 7.设函数 f （x）=， 若 f （x0）> 1 ，则 x0的取值范围是（ ）.

A.（-1，1）

B.（-1，+∞）

C.（-∞，-2）⋃（0，+∞）

D.（-∞，-1）⋃（1，+∞）

分析：本题主要考查了分段函数不等式的解法.采用常规方法求解，需分两种情况进行讨论，过程较为繁琐，于是根据函数的解析式画出图象，在图中寻找函数值大于1的曲线段，求得对应的自变量的取值范围，即可解题.

解：作出函数 y =f（x）的图象和直线 y =1，如图8所示，

由图可知，它们有2个交点，

令 f（x）=1，解得 x =1或-1，则其交点为（-1，1）和（1，1），

由 f（x）>1得 x <-1或 x >1.故本题选D项.

例8.解不等式 >x .

解：令y1= ，y2=x，

要使>x，需使 y1= 的图象在 y2=x 的上方.

由=x，可得 x =2或-2，

由图9可知，不等式的解集为{x|-2≤ x <2}.

将不等式左右两边的式子看作一条曲线和一条直线的方程，画出其图形，分析曲线和直线的位置关系，即可求得不等式的解集.

由此可见，数形结合思想在解高中数学题中应用广泛，灵活运用数形结合思想，将抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来，“以形助数”“以数解形”，能使问题快速获解，让解题变得更加高效.

（作者单位：四川省成都市新都一中）