深水区大截面海底电缆打捞受力分析

2022-03-24李晓骏张维佳左干清但京民李健王清简名才

应用科技 2022年6期

李晓骏，张维佳，左干清，但京民，李健，王清，简名才

1.中国南方电网有限责任公司超高压输电公司广州局，广东广州 510000

2.中南电力设计院有限公司，湖北武汉 430000

3.大连理工大学海洋科学与技术学院，辽宁盘锦 124221

海底电缆是铺设于海底，由绝缘材料包裹用于电力信号传输的关键装备。海底电缆工程主要包括设计、制造、存储、安装、在位运行和抢修等多个环节[1]。随着我国海底电缆应用的逐渐增多，海底电缆发生故障的概率也随之增加。其中海南联网工程海底电缆是国内第一条超高压、大截面、大长度充油海底电缆[2]。琼州海峡海洋气候多变，海底地质条件复杂，海面通行船舶众多，渔业捕捞和海上施工等人类活动频繁。海南联网工程在南方电网系统网架中地位重要，海南联网工程海底电缆一旦发生损伤，极易造成海南电网大面积停电。因此，必须建立应急抢修机制预案，在海底电缆故障后，能在最短时间内实施抢修施工和送电。深水区大截面海底电缆的抢修通常包括覆盖物清理、水下切割、电缆打捞和电缆回放等水下施工过程，其中电缆打捞是必不可少的环节。在电缆打捞过程中，除了需要保证抢修效率，还需要确保电缆的安全性，避免打捞过程中引发电缆的二次破坏。

目前关于海底电缆施工过程的线型与受力研究大多集中于在位和安装过程。陈金龙等[3-4]基于代理模型优化给出了极浅水在位线型受力分析及设计方法，针对铺设的一般过程，将铺设过程离散成若干典型工况，并通过非线性时域有限元法实现铺设过程的动态仿真分析。RUAN等[5-6]针对弹性海床上的深水缓波在位线型开展了静态受力分析研究，并基于多波形串联排布方法研究了深水缓波线型的疲劳损伤优化机理。闫宏生等[7]基于悬链线理论和集中质量法，采用简化模型对电缆正常铺设过程进行动态模拟，提出了相应的海底电缆安装环境条件。Cardoso等[8]提出了一种改进的钢悬链线线型的优化设计过程，该线型配置了流体动力阻尼器，以尽量减少压缩波造成的影响。蒲定等[9]基于专业水动力分析软件OrcaFlex 对中国南海某浅水浮式风机动态电缆进行线型设计与动态仿真分析，得出适用于该环境的动态电缆线型。Elsas等[10]提出应用贝叶斯优化(Bayesian optimization，BO)算法对初始在位线型进行有效优化的方法。刘淼儿等[11]以某海况的陡波线型设计为研究对象，以水面浮体的漂移域、线型最大曲率和经济性为设计指标，对于浮筒数量及线型设计开展研究。昝英飞等[12]建立了安装作业船舶-缆绳-刚悬链线线型动力学模型，计算分析了刚悬链线线型在提升过程中的弯矩变化，并详细分析了不同提升速率下的船舶运动、弯矩及收放缆顶端张力。Patrick等[13]研究了浮式风电电缆缓波线型安装过程的受力行为，对电缆安装过程中与浮体的连接、断开等工况进行讨论，验证了电缆安装的安全性。Zhao等[14]对半潜式海上风电机组（floating offshore wind turbine，FOWT）中多波线型动力电缆的动力特性和疲劳性能进行了研究，验证了多波线型的可行性。对FOWT 上2 个悬挂位置进行比较研究，结果表明，在极端海况下，多波线型有利于甲板箱处的较高悬挂点；而疲劳评估表明，较低的悬挂位置提供了优越的性能。

打捞过程的线型受力与在位和安装有所不同，曾昭磊等[15]通过对拖锚打捞的受力分析建立了数学模型，得到了打捞系统各组成部分的受力情况并对打捞锚进行定位。在打捞作业时，浮体的初始位置、行进/提升速度比（船体行进与起吊提升速度之比）会对电缆线型与受力产生较大影响，而打捞过程的受力分析问题尚未得到充分关注。开展电缆打捞提升过程的力学分析对合理选取上述参数、确保海缆打捞过程不受损坏尤为关键。本文将开展深水打捞过程电缆受力分析的理论和数值仿真研究，研究不同参数对电缆线型各位置的张力、曲率的影响。

1 打捞受力理论分析

海南联网工程充油型电缆的截面基本结构如图1 所示。电缆由功能层、铠装层、护套层等多层结构层间非粘接组合而成。电缆截面的设计及制造决定了其极限拉断力、最小弯曲半径等性能指标。海底电缆打捞过程中必须控制打捞线型各位置的张力、曲率满足相应指标要求，确保打捞过程中电缆的安全性。

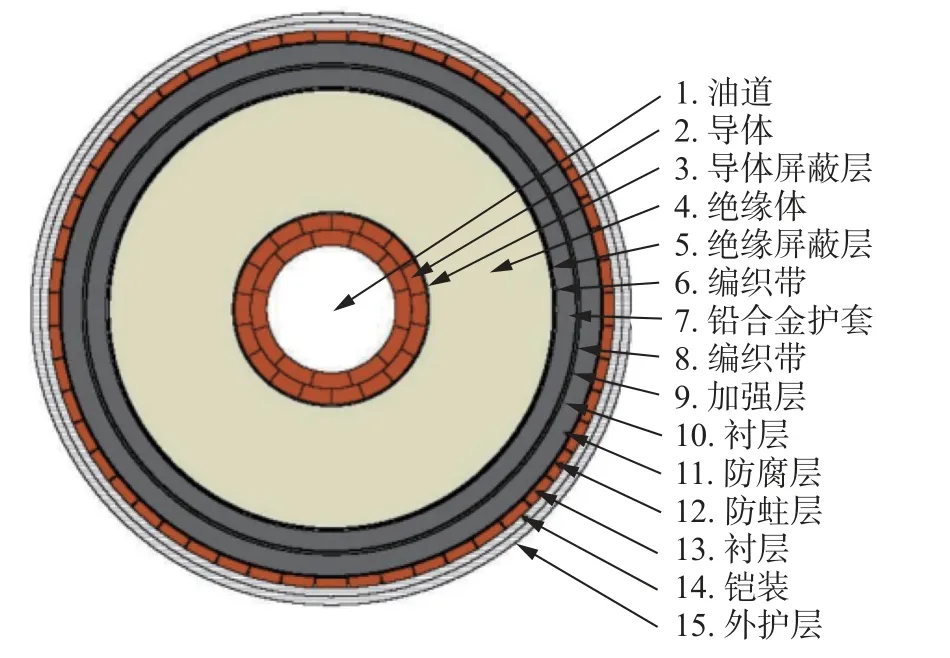
图1 充油型海底电缆基本结构

为对海底电缆打捞过程进行理论分析，需要建立理论模型确定打捞过程的关键力学参数。本文基于悬链线理论分析电缆各位置打捞过程的受力情况，忽略了电缆的弯曲刚度对线型的影响，假设电缆横截面位置只受张力作用，弯矩与扭矩的大小均为0。图2 为切割后海底电缆的打捞示意图，图中吊点为A，触地点为B，打捞水深为D，吊点高度为h，A、B2 点的水平距离为L0，β为吊点位置电缆与竖直方向的夹角。图3 为打捞过程中电缆的受力示意图，H为海底电缆张力的水平分量，该分量在悬链线上的任意一点均相等；V是海底电缆张力的垂直分量；Q是海底电缆在水中的单位长度质量，即电缆的湿重；LAB是电缆提起部分的总长度；dL为微元长度；k为悬链参数，表示悬链线触点到x轴的距离；θ为海底电缆任意点的提升角度。图4 为打捞器在吊点A处海底电缆的张力分解，TA为吊点A处海底电缆的张力，TB为海底电缆触地点B处海底电缆的张力。

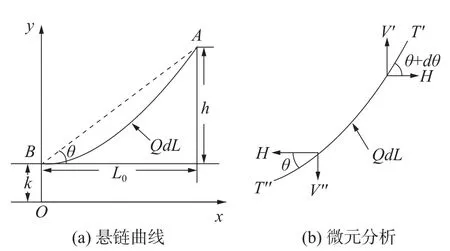
图3 电缆打捞过程受力示意

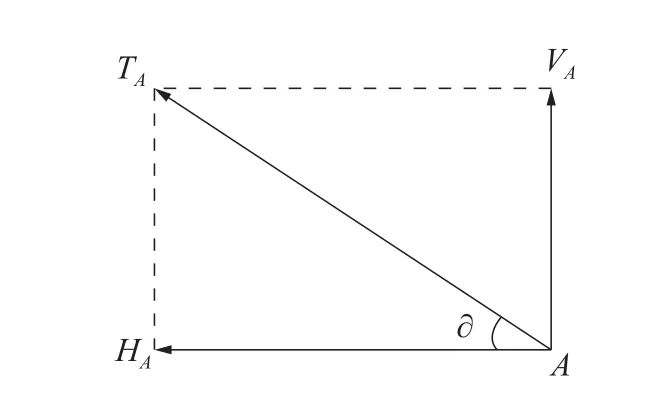
图4 吊点A 处海底电缆的张力分解

在打捞提升海底电缆时，吊点A和触点B之间的电缆在自重和外加张力的作用下处于平衡状态，海底电缆在A、B两点之间呈悬链线状，沿线各点均呈现一定弧垂，其悬链线方程为

式中：x、y分别为曲线的横、纵坐标；k为悬链参数，k=H/Q，取值为海底电缆张力的水平分量与海底电缆在水中单位长度质量的比值[15]。

由力的平衡原理可得悬链线的微元在平衡静态时的方程组如式(2)所示。其中悬链线中任意一段微元两端的张力分别表示为T′、T′′：

A、B两点之间海底电缆的悬链长度LAB为

海底电缆在吊点A处的张力TA可分解为

式中：HA为TA的水平分量，HA=H=HB；VA为TA的垂直分量；∂为吊点A处海底电缆的提升角度。

由于悬链线上任意2 点之间的张力差等于悬链单位长度的质量与这2 点间高度差的乘积，即

因此，在无波流等环境荷载作用下，提升切割后海底电缆的力学分析应满足式(3)的要求。

海底电缆上任意点的曲率K为

根据双曲余弦求导公式，整理得

由式(1)得出：

在吊点处的曲线的倾斜度等于打捞缆的吊点角度 β。提升电缆时，可以监测吊点角度 β，水深D为已知，由式(1)得出

从式(5)计算提升长度悬挂电缆总长度s(从吊点到触地点)为

沿缆曲率K整理得

根据上述分析，依据式(6)可求得打捞过程中电缆线型任意位置的曲率情况，判断电缆打捞过程中是否会发生破坏。

2 打捞受力数值分析

基于悬链线理论的分析过程进行了相应的假设，为了更真实地模拟打捞过程，本文建立了数值仿真模型。在此模型中，整体坐标的原点设在海平面上，Z轴方向垂直向上，X、Y轴方向满足右手定则，缆体布设方向在X轴正向。切割后海底电缆吊点A为自由端（刚性起吊0.5 m），另一端为固定点C，忽略抗弯装置的作用。根据近地点的最大曲率出现的位置将提升过程中的海底电缆分为上弯段和下弯段。为了提高分析精度，将海底电缆划分为2 部分，根据应用集中质量法将首10 m离散成若干长度为 0.1 m 的单元，剩余部分离散为 1 m 的单元，计算海底电缆切割后提升过程的主要力学响应。

集中质量法是分析管缆等细长结构常用的方法，将动态电缆划分为一系列线段组成的LINE模型，每个线段只能模拟电缆的轴向和扭转性能，而质量、重力、浮力等其他性能全部集中到节点上。需要特别指出的是OrcaFlex 软件中LINE模型区别于一般集中质量模型，考虑了构件的阻尼特性，利用弹簧和阻尼器的组合方式模拟动态缆，使得响应模拟的结果更真实。对于动态缆的动态响应，求解结构的响应方法有隐式解法和显式解法，2 种方法都是在每个时间步结束时求解系统的运动方程。隐式算法中，由于位置、速度和加速度在时间结束时是未知的，需要迭代，故在每一时间步内耗时大于显式求解。但是对于时间步较长的情况，隐式求解更稳定、效率更高。故本文对动态电缆的动力计算均采用隐式求解法，建立的电缆打捞仿真模型如图5 所示。

图5 电缆打捞仿真模型

3 结果对比与参数讨论

3.1 结果对比

本文以某海域的充油型海底电缆为研究对象，该型海底电缆主要应用于穿越河流、海峡的大容量输电，海底电缆的外径为0.14 m，轴向刚度为1.94×105kN，弯曲刚度为3.06 k N·m2，扭转刚度为19.54 kN·m2，最大张力为62.5 kN，允许最小弯曲半径为5 m，空气中质量为48 kg/m，海水中质量为33 kg/m。

由式(3)可得，张力沿海缆分布，吊点处产生张力极值。当TA>TP（TP为安装最大张力）时，电缆拉伸失效。为避免电缆拉伸失效，则海底电缆在不同提升高度时的最大吊点角度为βmax=，分析可得：随着吊点提升高度的增大，吊点角度最大值减小，则需要设计合适的行进/提升速度比，防止电缆拉伸失效；若在海底电缆提升过程中，在不同提升高度时，吊点角度始终保持βmax>β>βmin，则海底电缆不会发生因拉伸失效和弯曲失效导致的二次损坏。

采用理论模型对电缆打捞过程进行分析，其中Q=323.6 N，H=100 m，TB=25.9 kN，水阻力为零。首先依据k=H/Q计算悬链线参数k的取值，然后依据式(4)，以电缆长度s为横坐标，曲率K为纵坐标，采用MATLAB 软件进行拟合，绘制电缆的曲率分布图。OrcaFlex 软件模拟也可得到曲率沿缆分布图，将理论分析与数值仿真结果绘制在一张图中，如图6 所示。

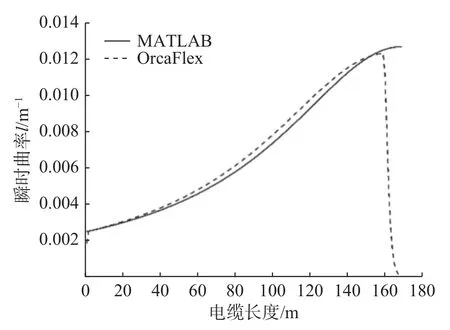
图6 水深为100 m 的沿缆瞬时曲率分布

如图6 所示，从整体曲率来看，理论分析与数值仿真结果接近，且由于数值仿真模型考虑水动力、缆的弯曲刚度和局部位置处海底刚度等影响，数值讨论更精确。特别是在触地点之后电缆平铺在海床上，曲率值为0，而触地点前电缆悬空产生了较大的曲率，所以有限元分析的触地点前后曲率会出现一个急剧的变化。OrcaFlex 曲率在近地点处骤减，悬链线理论局部位置存在误差，因此后续的分析采用OrcaFlex 数值仿真的方法进行研究。

3.2 浮体初始位置对捞过程的影响

浮体的初始位置决定海底电缆提升过程吊点角度的大小（特别在初始阶段），从而影响海底电缆沿缆曲率的大小。水深为100 m，行进/提升速度比为0.9，起吊速度为0.2 m/s 时，讨论浮体初始位置分别为0、30、60 m 的电缆曲率分布情况，如图7 所示。可以看出，海底电缆提升过程中，与吊点位置较近处的电缆曲率较大，在电缆前端出现曲率极值。因此在真实提升过程中，可通过抗弯装置降低此处的曲率，也可通过浮体初始位置控制曲率。海底电缆提升过程的曲率极值对浮体初始位置的变化灵敏。

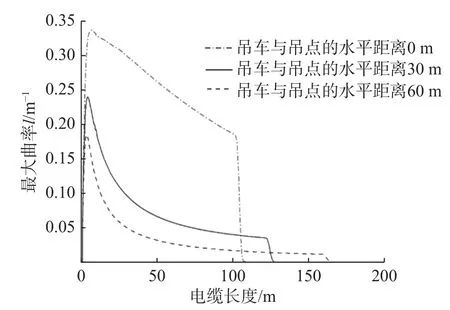
图7 吊车水平位置对海底电缆最大曲率的影响

浮体初始位置变化对海底电缆最大有效张力的影响如图8 所示。

图8 吊车水平位置对海底电缆最大有效张力的影响

结果表明，电缆提升，在吊点处出现张力极值，且对浮体水平位置的变化较灵敏。张力极值随吊点角度的增大而增大，故在设计时，选择合适的浮体初始位置和控制吊点角度的大小可以避免由于海底电缆提升出水面时张力过大而导致发生拉伸失效的问题。

电缆打捞过程中，增大浮体与吊点之间的水平距离，即增大吊车与吊点间的距离，沿缆的最大曲率明显减小，张力明显变大。

3.3 行进/提升速度比对打捞过程的影响

当水深为100 m，浮体初始位置为60 m，起吊速度为0.2 m/s 时，计算浮体行进速度与吊起速度的比值分别为0.7、0.8、0.9、1。相应的海底电缆前端的曲率极值随着行进/提升速度比的增大而增大，吊点提升高度为100 m 时，近地点的最大曲率随着速度比的增大而增大，变化明显，如图9 所示。若速度比持续增大，沿缆的曲率极值发生在电缆打捞出水面时的近地点，此时极易发生电缆弯曲失效。

图9 行进/提升速度比对电缆曲率的影响

行进/提升速度比的变化对沿缆最大有效张力的影响如图10 所示。

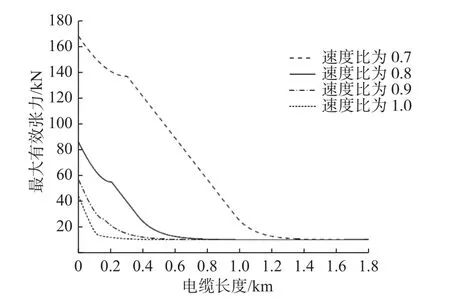
图10 行进/提升速度比对沿缆最大有效张力的影响

可以看出，沿缆分布的最大有效张力随速度比的增大而减小，海底电缆前端对应速度比的张力差随着速度比的增大而减小，这是符合实际情况的。根据文中理论分析可得，海底电缆湿重和吊起高度保持不变时，垂直张力分量保持不变；速度比增大，吊点角度减小，海底电缆悬链线总长度减小，近地点曲率增大，下弯段电缆倾斜角度减小，离地点水平张力减小，从而减小了对海缆前端张力极值的要求。

为了防止拉伸失效，可以通过控制浮体行进速度与起吊速度的比值来控制电缆悬链线长度，从而达到控制电缆最大有效张力的目的。随着速度比的增大，张力极值减小，近地点的最大曲率和沿缆的曲率极值增大，当速度比过大时，会发生弯曲失效。