浮体的平衡与稳定性研究分析

王宏飞 曾昕萌 刘 涛 李株丹

(华北水利水电大学， 河南 郑州 450046)

0 前言

人类对浮体的平衡和稳定问题很感兴趣，在古欧洲文明中阿基米德就在其论著中对浮体在液体中的平衡和稳定性作了系统的研究，斯蒂文也曾判定浮体排开液体的重心和浮体的重心应该在一条直线上，但错误判断为排开液体的重心应该在浮体的重心之上，否则就会翻转180度，惠更斯用数学方法对浮体的平衡性和稳定性进行了研究，认为浮体位置发生变化而转换到另外一个位置时，其重心和浮心的高度差将减小。欧拉和柏努力也都对浮体的稳定和平衡性作过细致的研究，并重新定义了小扰动和力矩恢复的概念，布格则在世界上首次对定倾中心作了定义，在现代科学领域定倾中心已经成为判定浮体稳定和平衡的一个重要参数，并在水利工程设计中得到了大范围的应用。

1 浮体的平衡和稳定性分析

在实际应用中，在一些科技文献中对定倾中心的概念定义比较模糊，例如，有的科技工作者认为浮体一旦发生细微变化，浮轴和浮力的作用线在一个固定点上相交，也有的科学家认为只有在实验室中上述两条直线才可能在一个固定点上相交；另外，用力系简化方法研究分析定倾高度的方法也不够科学严谨，有人甚至对稳定性的判定条件分析都出现了错判，带着这些问题作者翻阅了大量的中外科技文献，并结合了具体的案例对定倾中心概念作了明确的定义，对浮体的稳定性和平衡性作了判别，最终提出了用定倾高度判定浮体是否稳定的科学依据。

假设浮体的比重一旦低于水的比重，那么就会发生有的物体部分露出水面同时漂浮在水中，满足这些条件这种物体则称为浮体，浮体在水中平衡则要满足两个条件：第一、浮心和浮体的重心的连线和水平面相垂直。第二、浮体的重量等于水的浮力。如图1（a）所表现，浮体平衡位置也要能够保证一些稳定条件。如图1（b）所示，一个长方形的物体在竖立和平衡位置时，外界因素对其进行了干扰，左边物体的重力和浮力阻碍了物体失衡的因素，因此平衡没有被打破，而重力和浮力导致右边的物体发生偏移，因此其平衡是不稳定的，以下对浮体平衡和稳定的条件进行研究分析。

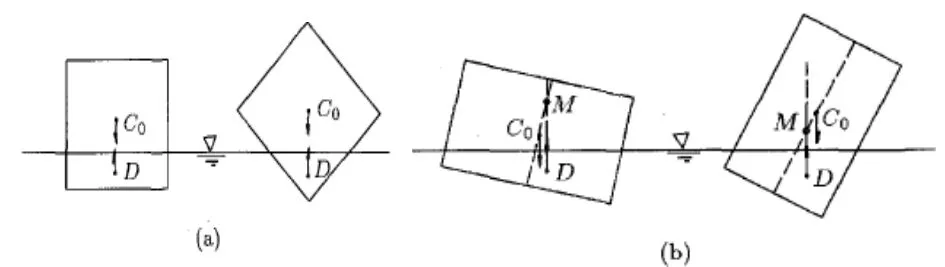
图1 浮体的平衡

假设浮体有一个虚拟的对称面，受外界因素干扰平衡位置会发生变化，浮体上每一个点相对于对称面作平行运动，浮体不受铅直扰动的干扰，而水平运动则会干扰浮体，如果考虑浮体稳定性会受到转动方向的影响，那么就可以把浮体在平衡状态下与水平面的相交面定义为浮面，并可以记作S。如图2所示可以建立一个浮体坐标系，并把浮面的重心定义为原点，并把浮面与对称面的相交直线定义为浮线，并定义为X轴。浮轴Y轴垂直向上，Z轴与X轴、Y轴正交，图2中阴影部分微元体的体积分：

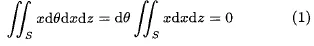
因为Z轴是通过S形心的主轴，所以（1）式成立，即浮体围绕Z轴发生动作时，浮体排开水的体积不发生改变，其受到的作用力也不发生变化。

平衡位置一旦受到外界干扰发生细小的变化，水覆盖浮体的位置也会受到影响而发生变化，受到的浮力也会发生改变，浮心的位置也会发生变化，杜宾定律表明，过D点的水平线是浮心曲线在这个点的切线，浮力作用线是浮心曲线在该点的法线，当D点和于Do点无限接近时，浮力作用线和直线Z的交点接近于该直线上的一个固定点，这个点被定义为定倾中心，如图1（b）所示，若浮体重心在定倾中心之下，浮力和重力形成了一个恢复力矩，浮体平衡稳定，若浮体重心在定倾中心之上，他们的力矩是排斥的，则不能保持稳定。如图2所示，定倾中心和浮力重心的高度差被定义为定倾高度，当高度为正时，浮体平衡保持稳定，若高度为负时，浮体失衡。

图2 定倾中心与浮心

如图2所示，以Do为坐标原点，建立直角坐标系，其中X1轴、Y1轴和X轴、Y轴平行且方向相同，则D点坐标如下：

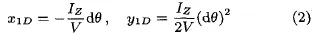
其中，Iz为平衡时的惯性矩，V为排开水的体积，由式（2）得

其中，do为浮心曲线的弧长，得

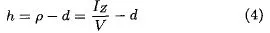
例1如图3（a）所示，在水面上漂浮一个正方形，可以尝试判定浮体是否平衡

解法1：假设木块达到平衡后的吃水深度为b,由平衡条件（i）得

由式（5）得

由式（6）得

2 浮心曲线研究

如果正方形有两个点被水覆盖时，浮心曲线是一条抛物线H（图4），曲率中心的运动轨迹有一个顶点M，浮体的重心到浮心曲线任一条法线对应一个平衡点，对某一平衡位置而言，假设浮体重心在浮心和定倾中心之间，浮体排开水的势能为最小值，则平衡是稳定的，假设浮体重心在浮心和定倾中心之外，浮体排开水的势能为最大值，则平衡是不稳定的，浮心曲线是封闭的，浮心曲线到浮体重心法线可以判定浮体是否稳定，在这种环境下两者之间的距离为一个极限值，每一个浮体都会有一个稳定和一个不稳定的状态，并且是相互分离的。

3 结论

上文所研究的仅仅是浮体一个方向晃动稳定性的问题，如果研究的是海上船只这种三维浮体，在把环境因素考虑进去，那么这就形成了一个复杂的问题。这些问题已然成为非线性动力学所探究的层次，我们对附体研究可以说是忠实的粉丝，这个探究从未中断过。而且方法和兴趣丝毫没有减弱，不仅仅增加了人类对大自然的认知，而且也加大了对大自然的掌控。

[1]刘德刚.非粘性流体力学.哈尔滨：哈尔滨工业大学出版社,2012.

[2]魏小青.浮体的力学研究》.上海：复旦大学出版社,1999.