基于超声反射法的液体粘度在线测量技术研究*
2022-03-24汪睦涵傅段发阶蒋佳佳张征宇
汪睦涵傅 骁*段发阶蒋佳佳张征宇
(1.天津大学精密测试技术及仪器国家重点实验室,天津 300072;2.中国空气动力研究与发展中心,四川 绵阳 510700)
粘度是液体的一种重要的物理化学性质,可由剪切力与剪切速率的比值来表征[1]。粘度作为流体热物性数据的重要参数之一,在许多工业部门和科学研究领域中都具有重要意义[2]。传统的粘度测量方法包括旋转法、落体法和振动法等[3],广泛应用于一般环境下的粘度测量中。然而,随着工业水平的发展,在某些特殊场景下进行粘度测量时,传感器或测量装置不能接触液体内部,因此传统的测量方法不能适用。
近年来,一些新型的粘度测量方法展现了其在不同环境下测量的优越性以及良好的发展前景[4-6]。光学技术的发展促进了以光学为基础的新型粘度测量方法,Alexis I Bishop[7]等利用旋转激光捕获的粒子进行光学方式的微观流变学研究,这种方法可以用于测量原型细胞结构内部的粘度,然而难以得到合适的双折射粒子,且校准捕获激光束的功率困难,导致粘度测量效果偏差增大。李南洋[8]等则研究了基于电磁感应的实时在线测量方法,测量精度最高可达7%,然而该方法仅适用于测量带电粒子粘度,不具有普遍性。
利用超声波进行粘度测量的方法也有了较大的进展[9-11],超声传感法是一种利用液体粘度与其超声阻抗谱存在相关关系,通过测量液体超声阻抗谱实现粘度测量的新方法[12-15],其特点在于能够实现在线实时测量,且相对于其他测量方法,对测量环境的要求不苛刻,能够在各种不同条件的环境下应用。在特殊环境下的液体粘度在线测量应用中,由于流体所处环境恶劣,且液体厚度较小,超声传感法则可以在不接触液体上表面的情况下,将超声粘度传感器安装于盛放液体的固体介质表面,通过发射和接收超声信号,实现特殊环境下的液体粘度测量[16-18]。然而利用超声传感法测量液体粘度时,固体匹配材料的声阻抗选取对测量范围及测量灵敏度等都会造成很大的影响,根据实际测量条件选择出最适合的匹配材料可以显著改善测量效果,具有非常重要的意义,因此本文发展了一种基于超声横波反射的液体粘度测量方法,通过引入固液声阻抗比值构建了反射系数与声阻抗比值的关系模型,计算求解了声阻抗比值与测量范围和灵敏度之间的关系,并给出固体匹配材料的选择依据,使测量环境得到进一步优化,最后通过仿真实验对理论分析的结果进行了验证。
1 基于超声波反射法的粘度测量原理
1.1 测量原理及模型分析
超声粘度测量原理如图1所示,超声传感器发射的超声横波通过固体表面并穿过固体后,垂直入射到固/液界面,一部分剪切波透过界面传输到液体中,另一部分剪切波在界面发生反射并返回固体中。反射波的幅值和相位与两种介质之间的声阻抗有关,反射波与入射波之比即为反射系数。在界面处入射波声压P i和反射波声压P r可由下式表示:

图1 超声横波在固/液界面反射模型

式中:A i和A r分别为入射波和反射波的幅值,ω为声波的角频率,φi和φi为入射波和反射波的相位,反射系数的幅值r和相位角θ可由下式表示:

根据反射原理,声波在固液界面的复反射系数为[19]:


式中:ρL为液体密度,G*=G″+jG‴为复剪切模量。G″为储能模量,G‴=ωη是损耗模量,η是粘度,ω是波的角频率。假设液体是牛顿流体,则储能模量为零,式(6)变为:

将式(7)代入式(5),由等式两边虚部和实部相等可得:

解式(9),有:
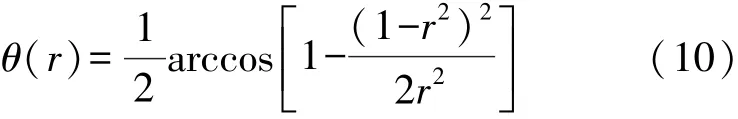
所以粘度与反射信号幅值之间的关系为:

因此,可以根据入射波和反射波的幅值求解出反射信号幅值,并进一步求得待测液体的粘度。
1.2 测量范围分析
进一步分析反射系数与两种介质声阻抗之间的关系,设液体声阻抗的模长则其复阻抗固体声阻抗的模长把和Z s代入式(5)可得下式:

从式(12)中可以观察到反射系数仅与l和s有关,因此测量某液体粘度时,固体材料也可称为对该液体的声阻抗匹配介质。为了更为直观地分析固液声阻抗匹配程度对反射系数的影响以及反射系数的变化规律,定义固液声阻抗之比代入式(12)可得:
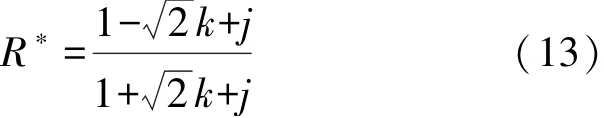
则反射系数幅值r可由下式来表示:

由式(14)画出r-k关系曲线如图2所示。由于k∈(0,+∞),所以且当,求解可得k=1时取最小值2,r有最小值2-1。k值代表了固液声阻抗之间的匹配程度,当k为1时,固体与液体的声阻抗相等,固液声阻抗匹配程度达到最大,此时反射系数达到了最小值。当k趋近于0或无穷时,固液两相的声阻抗匹配差异最大,在界面处的反射系数r越趋近于1,说明此时声波几乎发生了全反射,例如超声波在固体与空气界面发生反射时,由于空气的声阻抗远小于固体材料,所以其反射系数可以视为1。

图2 反射系数r与声阻抗比k的关系曲线

通过对比发现式(15)与式(14)的形式相同,表明当k=k′=α时,反射系数r的值相等。因此该曲线在k=1的左右两边呈现一种对应的关系,即k=α的点与k=1/α的点所对应的反射系数值相等。由反射系数关系模型可知,若固体声阻抗与液体声阻抗的大小关系不确定时,同一个r值点可对应两个k值点(k1=α与k2=1/α),分别代表了两种固液声阻抗的大小关系则通过反射系数可以求解出两个不同的粘度。当测量某未知粘度的液体时,虽然不知道其粘度的精确值,却可以估计出大致范围,为了使测得的粘度值唯一,应确保匹配介质的声阻抗应大于待测液体声阻抗所在范围内的最大值,即图2中k>1所表示的区域,因此可测范围内液体的声阻抗上限值为|Z S|。当固体声阻抗越大时,理论上测量上限也提高了。然而在实际测量时,大多数液体声阻抗相对固体而言较小,所以当固体声阻抗高达一定程度时,测量量程就可以满足绝大多数液体的测量要求。在图2中k=1附近的区域,曲线的斜率接近于0,反射系数r随k的变化不灵敏,当选定固体材料后,这种现象表现为反射系数因液体声阻抗变化而导致的变化量很小,测量灵敏度很低,因此选取匹配材料时应避免k值接近于1。这也表明选择匹配介质的材料时,除了考虑测量范围外,还应分析灵敏度对测量效果的影响。
1.3 反射系数灵敏度分析
反射系数的灵敏度表现为当粘度发生微小变化时,反射系数的变化量大小,在这里可反映为反射系
数r对粘度η偏导数的绝对值,即设反射系数灵敏度为A,可下式来表示:


式(17)中r对l求导可得:

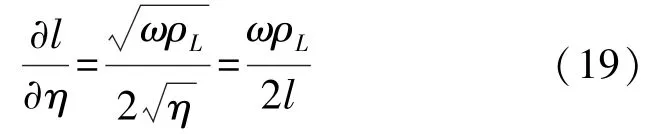
把式(18)(19)代入式(16)可得:

由式(20)可知灵敏度A也是以s和l为变量的二维函数,因此灵敏度的大小同样由液体与固体的声阻抗两者共同决定。
把s=kl代入式(17),可得如下结果:

把式(21)中关于k的多项式分离可得:

假设当测量某确定粘度的液体时,液体声阻抗l一定,由式(21)可知这时灵敏度值A仅由k决定。由于s=kl,当l一定时,不同的k值代表了不同的固体声阻抗s,因此可直接分析采用不同声阻抗的材料时对测量这种液体的灵敏度影响。由于为常量,通过分析|T|的值即可得到A的变化趋势,|T|越大代表灵敏度值越大,画出T-k曲线如图3所示。
由图3可知,曲线存在一个极小值点和一个极大值点,对T求导数得到T′,且令T′=0,可得k1=和分别对应着图中的两个极值点。把k1和k2分别代入式(22)可得:


图3 T-k关系曲线
式(24)(25)表明k=k1与k=k2的两点处灵敏度相同,且同时达到最大灵敏度Amax。根据上一节的分析,k值应大于1,因此这里应选择作为使灵敏度达到最大值的k值,若定义特征阻抗值点Z m是使灵敏度达到最大的固体匹配介质声阻抗,则的值与液体粘度有关。从式(25)中可以看到,随着l值的减小,也就是待测液体粘度的减小,测量时可能达到的最大灵敏度增大,所以理论上测量低粘度液体测量效果更好。然而待测液体粘度η减小后|也减小了,同时达到最大灵敏度的|Z S|也相应地减小了,由于现实中可能并不存在声阻抗这样小的固体,所以测量较低粘度液体时不一定能够达到其最大灵敏度,还需要综合考虑实际情况进行选择。再令T(k)=0,可得k0=1,这个点为曲线上的零点。此时灵敏度最低为0,表明当固液声阻抗相等时,粘度的微小变化将不能引起反射系数的变化,测得的粘度值灵敏度最低,因此选择匹配材料时应尽量避免测量时固体与液体的声阻抗相近。
若把l=k-1s代入式(21),可得如下结果:

式(26)表明,当选定固体匹配材料后,固体声阻抗s一定,则灵敏度值A仅取决于k。把式(26)中关于k的多项式分离可得:


图4 P-k关系曲线
在图4中,k>1的区域代表了有效测量范围。在此范围内,当k值增加时,|P|增加了,说明此时灵敏度增大。而当固体声阻抗一定时,k值增加表示液体声阻抗减小,由此可得到结论:选定匹配材料后,测量低粘度的液体灵敏度更大。
2 仿真实验及分析
2.1 匹配材料对测量范围的影响
分别使用石墨(Z S=2.98×106N·s/m3)、PMMA(Z S=1.72×106N·s/m3)和聚四氟乙烯(Z S=1.28×106N·s/m3)这三种材料作为匹配材料,根据式(17)画出r-l的图线如图5所示。

图5 不同固体介质下的r-l曲线
由图5可知,使用不同固体材料作为匹配材料时,反射系数均可以到达同一个最小值,约为0.414。而不同声阻抗的固体达到反射系数最小值时的液体声阻抗不同,仿真结果符合前面的理论分析,即当k=1即|时,反射系数取最小值
曲线最低点左侧为实际的测量范围,固体声阻抗越大时,曲线最低点更靠右端,此时测量的量程也越大。从图5中可以看到,三种材料中使用石墨作为匹配材料时的测量范围最大,而使用聚四氟乙烯时测量范围最小。
2.2 匹配材料对灵敏度的影响
选取不同粘度的液体和不同声阻抗的固体进行仿真测量实验,计算其灵敏度的值。实验中超声波发射频率设为5 MHz,分别测量粘度为5 Pa·s和10 Pa·s,密度为1 g/cm3的液体,使用铝、花岗岩、石墨、PMMA和聚四氟乙烯5种材料作为匹配介质,计算出测量该液体时的灵敏度如表1和表2所示。

表1 测量5 Pa·s粘度液体的灵敏度

表2 测量10 Pa·s粘度液体的灵敏度
由表1和表2可知,使用声阻抗较高的匹配材料时,虽然测量范围会增大,但是灵敏度较小。
测量粘度为20 Pa·s,密度为1 g/cm3的液体,计算测量该液体时的灵敏度如表3所示。

表3 测量20 Pa·s粘度液体的灵敏度
由表3可知,虽然PMMA的声阻抗高于聚四氟乙烯,但是灵敏度反而更大,与表1的规律不符,这是由于当测量粘度为20 Pa·s的液体时,计算其特征声阻抗值由于PMMA的声阻抗比其他材料更接近Z m,因此测量时灵敏度更大。
测量粘度为50 Pa·s,密度为1 g/cm3的液体,计算测量该液体时的灵敏度如表4所示。

表4 测量50 Pa·s粘度液体的灵敏度
通过观察表4的结果可知,使用石墨作为匹配材料时的灵敏度最大。这是因为测量粘度为50 Pa·s的液体时,Z m=3.025×106N·s/m3,通过观察可知,随着待测液体粘度从20 Pa·s增大至50 Pa·s,Z m的值也增加了,此时声阻抗最接近于Z m的材料由PMMA变为石墨,因此用石墨作为匹配材料时灵敏度最大。使用聚四氟乙烯测量50 Pa·s粘度液体时灵敏度极低,证明了当待测液体粘度接近测量范围的界限时,灵敏度会趋近于0,测量效果不佳。通过对比表1、2、3、4可知,用同种材料测量高粘度液体的灵敏度明显低于低粘度液体,其结果与理论分析相符,因此当测量范围确定以后,若实际测量时有最低灵敏度标准,则只需使测量量程内的最高粘度液体的灵敏度大于其最低标准,那么测量此范围内任何粘度的液体时都会满足灵敏度要求。
3 与传统测量方式的对比
目前,粘度测量最为常见的传统测量方法有旋转法、落球法、振动法和毛细管法,这些方法均属于接触式测量方法,在不同测量领域分别具有其独特的优势。由于本文主要分析了超声反射法测量时的灵敏度和测量范围,而测量范围又与测量精度密切相关,结合本文的仿真分析,以及部分参考文献,将不同测量方法的测量精度进行对比,其结果如表5所示。

表5 不同测量方法的精度和测量范围比较
由表5可知,不同方法的测量范围不同,振动法和旋转法可以测量较高粘度的液体,毛细管法和落球法的测量范围相对较小,而超声传感法的测量范围适中。通过对测量精度进行对比,虽然超声反射法的精度略低于其他测量方法,但是其作为一种新型的粘度测量方法,与传统的测量方法不同,具有非接触式测量,在线测量等优点,适用于某些特殊环境下的粘度测量,因此具有重要的研究意义。
4 结论
本文针对基于超声横波反射的液体粘度测量方法时的固液匹配问题,建立了超声横波反射法测量液体粘度的反射系数模型,引入了固液声阻抗比值k,通过分析反射系数与k值的关系直观地反映了反射系数的变化规律,并确定了固液声阻抗对测量灵敏度的影响。使用3种声阻抗不同的常用材料作为匹配材料进行灵敏度仿真实验。结果表明,固体匹配材料的声阻抗对测量范围和灵敏度都有一定影响。使用声阻抗较高的材料可以增大测量范围,然而灵敏度却并不一定会增大,这是因为只有当固体介质声阻抗越接近特征阻抗值Zm时,灵敏度才会越大。由于Zm与待测液体粘度相关,因此应综合考虑待测液体粘度对测量范围和灵敏度的影响,筛选出最佳匹配材料。当匹配材料一定时,在测量范围内测量低粘度液体的灵敏度更高,说明该测量方法测量低粘度液体时较为灵敏。实际测量时可把仿真结果作为参考,优化测量条件,进一步改善测量效果。
