基于卷积网络的双热电偶动态温度测量方法

虞思思李文军崔志文金敏俊

(中国计量大学计量测试工程学院，浙江 杭州 310018)

工业、农业、国防等领域中存在测量动态温度的需求[1]。热电偶因其成本低、可靠性高等优点被广泛应用[2]。但热电偶存在热惯性，动态响应存在迟滞，动态温度测量存在动态误差[3]。为了减小动态误差，通常采用硬件补偿法和软件补偿法。硬件补偿法采用硬件电路进行补偿，存在通用性差等缺点。软件补偿法利用数据驱动的方式建立模型，对测量值进行修正，重建动态温度，具有补偿精度高、通用性强等特点。

双偶法通常使用两支具有不同时间常数的热电偶来重建真实温度[4]。Yanfeng Li等使用双热电偶来测量等速流动环境中的动态气体温度，并利用小时间常数热电偶的输出数据重构输入动态温度[5]。Xingyu Ren等用两个不同直径的细丝热电偶组成双热电偶探头对湍流乙烯扩散火焰进行高频温度测量，并补偿湍流气体温度[6]。Peter C Hung等提出了一种差分方程sDEd方法，利用两支热电偶的输出以解决高频波动的损失[7]。

物理传感器测量的动态流量、压力和温度[8]都可以看作时间序列。热电偶是测量温度的传感器，其测量的温度数据也可以看作时间序列。在时间序列研究中，自回归滑动平均模型(autoregressive moving average，ARMA)以及差分整合移动平均自回归模型(autoregressive integrated moving average，ARIMA)应用广泛。但是，这两种模型都属于线性数学模型，存在着诸多局限性，如线性模型只在线性关系问题中表现良好[9]。近年来，深度学习方法日益成为研究的热点。Lucas等通过卷积神经网络(convolutional neural networks，CNN)提取气象数据特征以计算日参考蒸散量[10]；Shi等将长短期记忆人工神经网络模型(long short-term memory，LSTM)引入降水量研究；Pradeep He wage等使用时间卷积网络模型(temporal convolutional networks，TCN)对气象数据进行分析[11]。

本文提出了基于卷积神经网络和基于时间卷积网络的双热电偶动态测温模型。将伪随机二值序列作为激励温度[12]，获得两支时间常数互异的热电偶在高低温双温度源激励下的理论测量值。将两支热电偶的理论测量值视为时间序列并作为CNN和TCN的输入，通过CNN和TCN重建动态温度，采用RMSE和R2对CNN模型和TCN模型的动态温度重建进行评价。搭建了双热电偶动态温度测量实验系统，以两支K型镍铬镍硅热电偶为实验对象，给出了一个算例。

1 双热电偶动态测温模型

1.1 基于卷积神经网络的双热电偶动态测温模型

卷积神经网络(convolutional neural networks，CNN)是包含卷积计算且具有深度结构的前馈神经网络，是深度学习的代表算法之一[13]。在时间序列建模中，CNN也表现出了良好的性能。

CNN的基本结构一般由输入层、隐藏层、全连接层以及输出层构成，隐藏层主要包含卷积层和池化层。基于卷积神经网络的双热电偶动态测温模型如图1所示。

图1 基于卷积神经网络的双热电偶动态测温模型

假设热电偶1测量值序列T1为{T1(k)｜k＝1，2，…，n}，热电偶2测量值序列T2为{T2(k)｜k＝1，2，…，n}，真实温度序列T r为{T r(k)｜k＝1，2，…，n}。CNN将序列问题转化为根据T1、T2去预测T r。

卷积层(Convlution)体现了局部连接和权值共享两种核心思想，有效的减少了网络的参数数量，缓解了模型的过拟合问题，使运算变得简洁、高效[14]。

局部连接，即卷积层中的节点只与前一层的局部节点相连，只学习局部特征。

权值共享意味着整个温度时间序列的元素都共享了相同的权值，即每个卷积核在遍历整个时间序列时，卷积核的参数值不变。不仅减小了模型复杂度，且很好的利用了元素间的局部相关性。

卷积操作可以看作在温度时间序列上应用和滑动卷积核[15]。与图像不同的是，卷积核只显示一维(时间)而不是二维(宽度和高度)，输入温度时间序列T1的卷积运算表达式为:

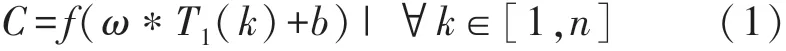
式中:“*”为卷积运算，k为时间序列长度，b为偏置参数，f为非线性函数例如校正的线性单元

(ReLU)。

池化层一般在卷积层之后。池化层通过池化操作进一步减少参数的数量，通过在温度时间序列的滑动窗口上聚合来减少其长度，简化模型的复杂性、提高计算速度以及提高所提取特征的鲁棒性。最常用的池化方法有最大池化(max-pooling)和平均池化(mean-pooling)。池化在防止过度训练和减少计算复杂度方面起着至关重要的作用。

卷积层参数误差会造成估计均值的偏移，而采用最大池化操作能够减小偏移带来的误差。假设输入为n H×n W×n C，经过最大池化操作后输出为:

式中:l为池化核大小，s为步长。

扁平化层(Flatten)将提取的特征转化为一维特征向量，然后使用联合层(Concatenate)将两个特征向量进行融合，最后通过全连接层(Fully-connected)进行输出。

1.2 基于时间卷积网络的双热电偶动态测温模型

时间卷积网络(Temporal Convolutional Network，TCN)，是一种能够处理时间序列数据的网络结构，是将CNN思想引入时序数据处理的一种新方法[16]。与CNN相比，TCN具有时间因果性和更灵活的感受野。基于时间卷积网络的双热电偶动态测温模型如图2所示。

图2 基于时间卷积网络的双热电偶动态测温模型

与CNN方法类似，TCN也将序列问题转化为根据T1、T2去预测T r。

TCN中的因果卷积与普通卷积不同，其一个时间的输出仅与前一层中更早时间的元素卷积，不考虑未来的信息。一个简单的因果卷积只能回顾一个网络深度上呈线性大小的历史，这使得将上述因果卷积应用于需要较长历史的温度时间序列时卷积层数会增加，而卷积层数增加会带来梯度消失、训练复杂及拟合效果不好等问题。为解决这一问题，TCN引入扩张卷积，使感受野成倍增大。扩张卷积又称膨胀卷积或空洞卷积，除卷积核大小外，扩张卷积还有一个参数即扩张因子d，用来表示扩张的大小，扩张因子d通常以2的指数形式增加，d＝2m，m∈{0，1，…，n}。输入温度时间序列T1中元素s的扩张卷积运算表达式为

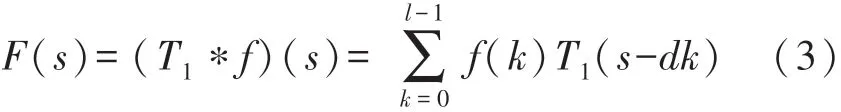
式中:“*”为卷积运算，d为扩张因子，l为卷积核大小。选择更大的卷积核和增加扩张因子d都可以增加感受野，使顶层的输出代表更广泛的输入。因果扩张卷积如图3所示，其中d＝2m，m∈{0，1，2}。

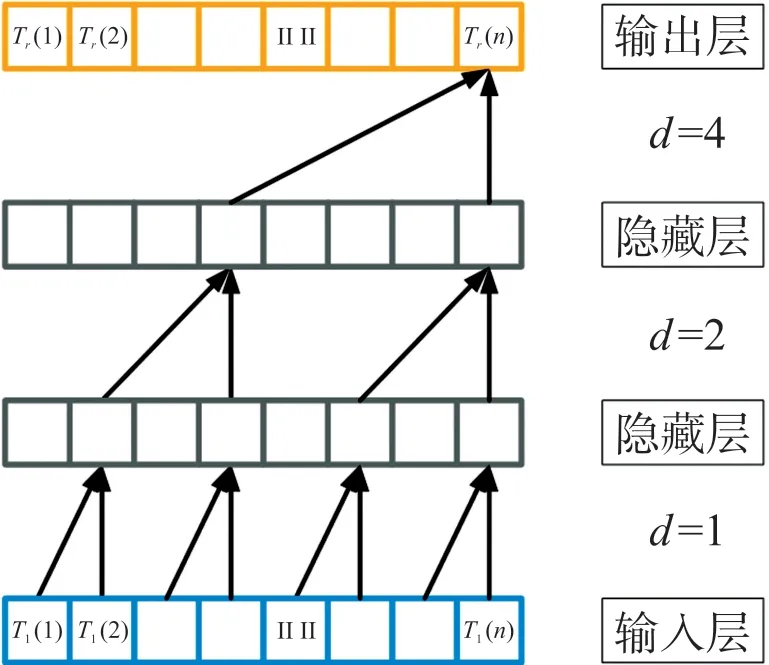
图3 因果扩张卷积

TCN的感受野取决于网络深度、卷积核大小和扩张因子，当输入数据量更大时，模型仍会非常深，因此提高模型精度、避免特征信息丢失过多，进而稳定更深层的时间卷积网络变得非常重要。TCN增加了残差连接使输入数据可以跨层被直接添加到输出中，因输入与输出数据可能维度不同，使用1×1卷积来确保维度的一致。

TCN通过堆叠若干个残差块来构造完整结构，每个残差块通常由若干层因果扩张卷积以及与之配套的权值规范化(WeightNorm)、激活函数、随机失活率(Dropout)和残差连接组成[17]。图4所示的残差块包含两层因果卷积以及与之配套的权值规范化、ReLU、随机失活率和残差连接。

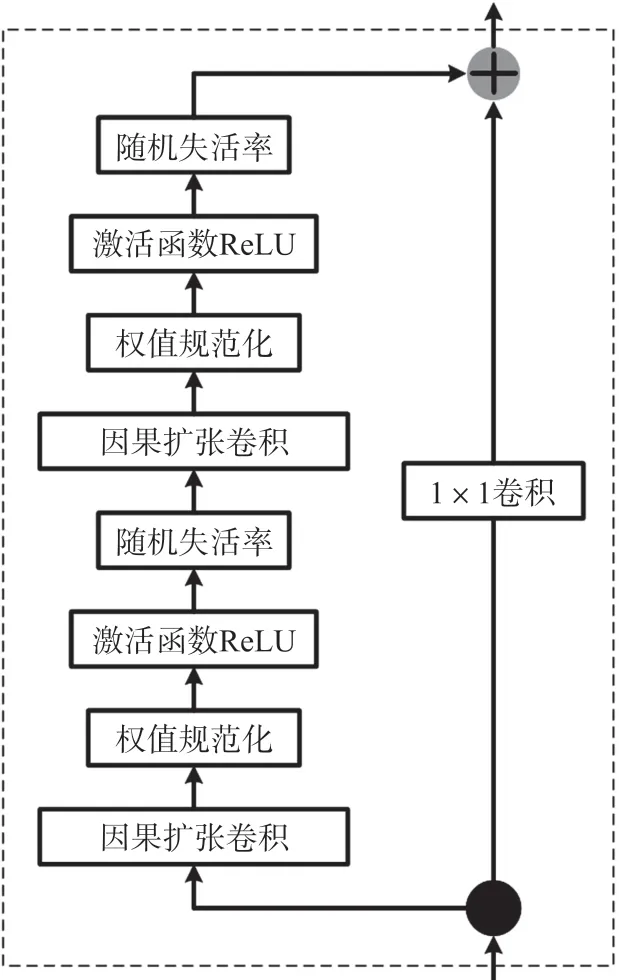
图4 残差块

1.3 评价指标

为了比较CNN和TCN模型动态温度重建的精度，采用统计指标均方根误差(Root Mean Square Error，RMSE)和拟合优度(Goodness of Fit)对两种模型进行评价。

均方根误差是模型预测值与真值偏差的平方与时间序列长度n比值的平方根，用来衡量模型预测值同真值之间的偏差。其表达式为

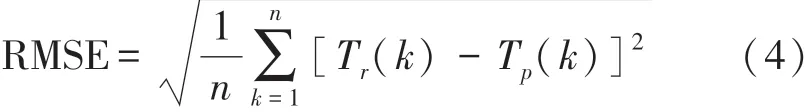
式中:n为时间序列长度，T r为真值，T p为模型预测值。均方根误差越小，说明模型预测的越准确；均方根误差越大，则越不准确。

拟合优度指模型预测值对真值的拟合程度。度量拟合优度的统计指标是可决系数R2，其表达式为

2 双热电偶动态测温仿真

2.1 热电偶理论测量数据集

Victor在测试热电偶动态响应性能时，采用伪随机二值序列(pseudo-random binary sequence，PRBS)作为激励温度[18]。因此，使用伪随机二值序列作为热电偶在高低温双温度源下的无量纲激励温度。如图5所示，y坐标表示无量纲温度，其中0代表低温温度源，1代表高温温度源。设定的采样频率为50 Hz，采样时间长度为200 s，数据长度为10 000。

图5 激励温度

根据Li[19]，假设热电偶1的时间常数τ1＝0.045s，则其传递函数为

将图5中的激励温度应用于式(7)的热电偶1，得到理想情况下的响应，如图6所示。

图6 热电偶1理想响应

为了使理论测量数据集更接近实际应用数据集，在上述数值中加入不同强度的高斯噪声，噪声大小可由信噪比(signal-to-noise ratio，SNR)控制，信噪比的定义如下

式中:P s和P n分别代表信号和噪声的有效功率。

本文以步长为10 dB，SNR在20 dB至60 dB范围内，获得多组热电偶理论测量值。热电偶1在SNR为20 dB和60 dB时的理论测量值如图7(a)、(b)所示。

图7 热电偶1在SNR为20 dB和60 dB时的理论测量值

类似地，假设热电偶2的时间常数τ2＝0.135s，则其传递函数为

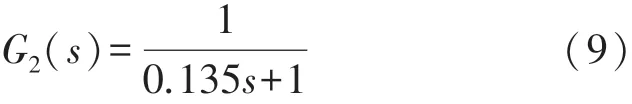
将热电偶1和热电偶2的测量值序列T1、T2作为模型的输入，真实温度序列T r作为输出。如图8所示，T1(k)、T2(k)分别为在k时刻热电偶1和热电偶2的测量值，Tr(k＋1)为在k＋1时刻的真实温度。具体而言，取[T1(k－1)，T1(k)，T1(k＋1)]和[T2(k－1)，T2(k)，T2(k＋1)]作为输入样本，T r(k＋1)作为输出样本，滑动窗口每次移动的距离为1。

图8 模型的输入输出样本

滑动窗口遍历序列后得到输入输出样本数据集，将其70%划分为训练集用于训练模型，30%划分为测试集用于测试模型。

2.2 卷积网络模型参数设置

2.2.1 CNN模型参数

两个序列利用卷积层和最大池化层完成特征的提取，经扁平化层将特征映射为一个一维向量，合并两个一维向量，通过适当的随机失活率缓解模型的过拟合问题，再通过全连接层进行输出。CNN模型的参数设置如表1所示。

表1 CNN模型参数设置

2.2.2 TCN模型参数

扩张因子d＝2m，m∈{0，1，2，3，4，5}。两个序列经因果扩张卷积完成提取特征后，利用权值规范化简化计算，再通过适当的随机失活率缓解模型的过拟合问题。TCN模型的参数设置如表2所示。

表2 TCN模型参数设置

2.3 计算结果

对热电偶1和热电偶2的测量值序列T1、T2进行CNN和TCN建模，重建动态温度。在SNR为20 dB时两种模型的动态温度重建如图9(a)所示，两种模型在3.2 s～12.8 s的动态温度重建与激励温度的局部放大如图9(b)所示。

在SNR为30 dB～60 dB范围内，步长为10 dB，两种模型在3.2 s～12.8 s的动态温度重建与激励温度的局部放大如图10所示。

由图9～图10可以看出，在SNR为20 dB～60 dB噪声环境下，两种模型的动态温度重建误差主要在温度阶跃处。且与CNN模型相比，TCN模型的动态温度重建更接近激励温度。

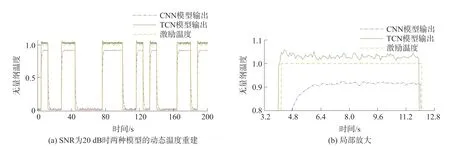
图9 SNR为20 dB时的动态温度重建

图10 SNR为30 dB～60 dB时的动态温度重建局部放大图

根据式(4)和式(6)，计算RMSE和R2，用于评价模型的精度，结果如表3所示。

由表3可以看出，在SNR为20 dB～60 dB噪声环境下，与CNN模型相比，TCN模型的RMSE更低，R2更高，表明TCN模型的动态温度重建精度更高。且随着信噪比的减小，与CNN模型相比，TCN模型的RMSE和R2更为稳定，表明TCN模型具有更强大的抗噪声能力。

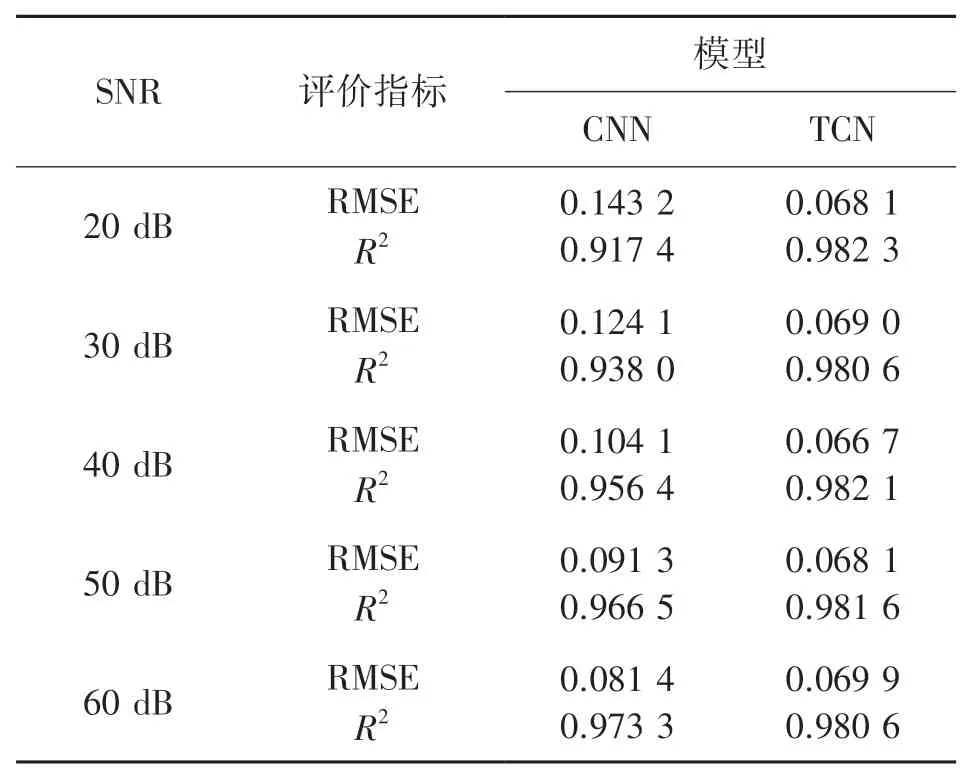
表3 在SNR为20 dB～60 dB噪声环境下两种模型的RMSE和R2

3 双热电偶动态测温实验

3.1 实验装置

搭建了双热电偶动态温度测量实验系统。实验装置包括上位机、数据采集卡、热风枪以及热电偶。双热电偶动态温度测量实验系统如图11所示。

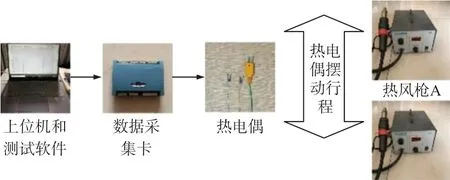
图11 双热电偶动态温度测量实验系统

K型热电偶具有灵敏度高、热电性能稳定等特点。因此，采用两支丝径比为2的K型镍铬镍硅热电偶为实验对象[20]，热电偶A的丝径为0.3 mm，热电偶B的丝径为0.15 mm。由于实验中真实温度变化未知，所以以高精度热电偶的测量值为标准，高精度热电偶的丝径为0.1 mm。

实验原理是利用两支热风枪A、B产生低温气流和高温气流，热电偶测温结点在两种气流间来回摆动，数据采集卡采集热电偶A、B的测量值TA、TB以及高精度热电偶的测量值Tr。

3.2 实验结果

设定热风枪A温度为50℃，热风枪B温度为250℃。采样频率为50 Hz，采样时间长度为200 s，数据长度为10 000。热电偶的实验测量值如图12所示。

图12 热电偶实验测量值

在建立模型前，对热电偶A、B的测量值TA、TB以及高精度热电偶的测量值Tr进行归一化处理，其表达式为

式中:Tmin为温度序列数据的最小值，Tmax为温度序列数据的最大值。热电偶测量值归一化如图13所示。

图13 热电偶测量值归一化

由图13可以看出，高精度热电偶的动态响应优于热电偶A、B，热电偶B的动态响应优于热电偶A。

对热电偶A、B归一化后的测量值进行CNN和TCN建模，重建动态温度。两种模型的动态温度重建与高精度热电偶测量值对比如图14所示。

由图14可以看出，CNN模型的动态温度重建误差主要在温度阶跃处。

图14 模型输出与高精度热电偶测量值对比

根据式(4)和式(6)，计算RMSE和R2，用于评价模型的精度，结果如表4所示。

表4 两种模型的RMSE和R2

表4中的实验数据处理结果是在与仿真一致的模型参数条件下获得的。由表4可知，采用双热电偶测量动态温度时，TCN模型的RMSE为0.028 4，R2为0.994 0，优于CNN模型，表明TCN模型的动态温度重建精度更高。且根据计算结果可知，热电偶B测量值与高精度热电偶测量值之间的RMSE为0.092 9，R2为0.938 9，因此TCN模型输出温度应优于热电偶B。

在相同的实验环境下，其他条件不变，改变两支热风枪的温度分别为50℃、300℃和150℃、250℃，获得两组新的实验数据，将得到的新的实验数据代入已训练好的TCN模型中进行预测，两组实验的RMSE分别为0.044 1和0.034 8，R2分别为0.983 3和0.989 2。因此已训练好的TCN模型对于其他真实实验温度，其预测效果同样较好。

4 结论

为了获得更精确的动态温度，提出了基于卷积网络的双热电偶动态温度测量方法。采用卷积网络中的CNN和TCN对两支同一材质不同丝径热电偶的测量值序列进行建模，重建真实温度。计算结果和实验结果表明，与CNN模型相比，TCN模型的RMSE更低，R2更高。因此，基于时间卷积网络的测量方法能够提高动态温度测量的精度，且结果优于基于卷积神经网络的方法。