大型油浸式变压器绕组温度场分布特征提取方法研究

殷 健

(1.青岛港国际股份有限公司，山东 青岛 266034；2.青岛新前湾集装箱码头有限责任公司，山东 青岛 266520)

0 引言

油浸式变压器是电力系统中最为关键、应用最为广泛的设备之一，为了使其性能能够满足大容量电网运行的需求，变压器结构原理和选用材料均需要不断创新和完善。即便如此，变压器仍需经过多方面考核才能投入使用，在运行的过程中也要定期检测和维修。温度变化情况是考核变压器性能的重要指标之一，每个变压器在投入使用之前都必须进行温升测试。温升的主要原因是变压器工作时，其绕组和铁心等内部构件出现损耗，并将这部分损耗转化为热量，导致变压器中各配件出现发热现象。经过长时间跟踪研究表明，大多数变压器损坏的主要原因为绝缘材料的绝缘性能丧失，温度则是主要影响绝缘材料性能的因素，温度过高就会破坏其绝缘性，过低又会使变压器利用不充分，因此，明确变压器是否处于合理温度条件内就成为研究热点课题。

全方位分析研究变压器的温度分布，准确地给出变压器内部配件的温升情况，提前发现引起过热现象的零件，并及时进行维修处理就变得尤为重要。刘刚等[1]采用混合法对变压器瞬态温度场进行模拟仿真，分别采用迎风有限元和有效体积法计算出了变压器的流体场和温度场，通过循环计算这2种数据模拟变压器的瞬时温度场；骆小满等[2]结合模糊神经网络计算给出了一种变压器温度场反演方法，首先通过有限体积耦合迭代确定流体-温度场，给出热点温度的具体范围，根据顶层油温、环境温度和外壳温度等特征构建模糊子集，完成变压器热点温度的计算以及温度场分布特征分析。

基于此，为了能够更清晰描述出变压器温度场情况，本文提出了一种大型油浸式变压器绕组温度场分布特征提取方法。首先对变压器的主要热源绕组、铁心进行分析，并给出二者发热量的计算方法；随后分析变压器的散热情况和散热能力，根据热源的发热及变压器散热能力的实际情况，计算出平稳状态下变压器内部构件的各个能量变化情况；进而推导出温度场分布情况，完成温度场分布特征提取。

1 变压器热源及散热分析

变压器内部构件在运转过程中会出现损耗[3]，进而转化为热能，不同部件的耐热能力不同，产生的温升极限也不同。由于绕组和铁芯分别为变压器中温度产生的主要热源，因此，需要对二者的放热以及散热情况进行详细研究。

1.1 绕组热源研究

绕组的热源是由绕组铜耗和涡流损耗组成[4]，铜耗的计算方法为

(1)

同时，绕组线圈如果处于漏磁场[5]中，也会产生一定程度的损耗，并转化为热能。因此，本文首先通过有限元法研究变压器的漏磁场状态，凭借ANSOFT瞬态场计算出绕组的漏磁分布情况，分析得出绕组高度方向的漏磁通基本呈纵向分布。导线的涡流损耗大小也与导体面积和磁场大小相关，则每个有限元的涡流损耗为

(2)

ρ为涡流密度；Bi为导线在有限元i单元中的磁通密度；ω为磁场涡流角频率；Ri为铁心中心点到i单元磁场中心的距离；Si为i单元磁场中导线所占面积；b为产生的辐向磁场大小。纵向涡流损耗为

(3)

s为纵向涡流单元；d为产生的纵向磁场大小。假设M为绕组单元数量，则绕组总涡流功耗为

(4)

那么铜耗与涡流损耗之和即为该绕组产生的总功耗，其表达式为

P=PD+PE

(5)

若在计算时，产生热量的热源为q，则有总热量为

qw=P/V

(6)

V为绕组体积。

1.2 铁心区热源

铁心的发热量也是不可忽略的，其总损耗是附加铁损与基本铁损之和[6]。基本铁耗P0的计算式为

(7)

K0为空载损耗系数；GF0为铁心的实际重量，F0为铁心的初始参数；Pc为单位重量下铁心产生损耗量；P1/50为损耗系数；β为介质的热膨胀系数，通常会根据变压器的实际情况在1.2～1.6之间取值；f为频率；Bm为最大磁密度。

1.3 变压器散热分析

变压器中温度呈不均匀分布，因此，为降低计算复杂度，将铁心和绕组视为均匀发热体，总结出其主要3种散热方式分别为热传导、对流和辐射散热[7]。根据变压器的实际参数以及环境信息，给出3种方式散热量的计算过程，作为温度分布特征提取的准备数据。

a.热传导计算。

实际变压的饼式绕组是由多个线匝构成，每个线匝之间均有绝缘纸隔绝，绝缘纸很大程度地影响热传导散热。传统的热传导计算为了减少计算量，往往会将每个饼线视为一个整体，忽略绝缘纸对其影响，使得计算结果准确度直线下降。因此，本文分析现阶段广泛应用的组合制绕组和普通绕组的实际特征，在热学原理的基础上，推导出以上2种常用结构绕组的平均导热系数，给出绕组的热传导计算方式。

设2个平行表面中的1个面积为S，两者间距为δ，若2个表面的恒定温差为θ1-θ2，则热传导的散热流量p计算式为

(8)

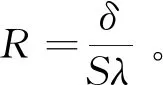
b.对流散热计算。

对流散热是油浸式变压器的主要散热方式，单位散热和冷却表面温度、冷却介质性能相关。采用油箱壁和空气的对流换热系数[8]h完成对流散热的求解。根据流体力学及传热学可得

(9)

L为油箱壁的高度；Nu为努塞尔数，即

(10)

Pr为普朗特数[9]；Ra为瑞利数，即

(11)

g为加速度；Tw为油箱壁温度；T∞为变压器内部能够作为散热导体的空气的实际温度；k为传热空气的导温系数；v为散热空气的动力粘度。

c.辐射散热计算。

在变压器的油箱内部，铁心、绕组传导给油的热量较少，可以忽略不计，但是油箱壁的散热量较大不可忽略，箱壁、箱壁周围以及辐射体的温度的关系为

(12)

qλ为辐射体温度；T1为箱壁温度；T2为箱壁周围介质温度；N一般情况下为固定值，其大小与辐射体表面情况相关，通常可取N=5 W/(m2·K)。

2 变压器温度场分布特征提取

当绕组和铁心损耗公里达到平稳状态时，热量产生和散失就会平衡，此时变压器内部的各个固体构件间的导热符合傅里叶热传导方程，即

(13)

变压器中固体-液体间对流换热[10]符合牛顿冷却原理，即

q′=h(tw-tf)

(14)

q′为固-液体总的对热换流量；tw为换热期间固体表面温度；tf为换热期间流体的散热温度。

若油和油箱壁间的固体温度低于流体温度，固体被流体加热，则又可以描述为

q=h(tf-tw)

(15)

油箱壁面和空气之间的关系为

(16)

ε为油箱热量的辐射率；σ为玻尔兹曼常数；A1为构件辐射面1的面积；Fj为交换面的形状系数。

则变压器的质量守恒方程为

(17)

vx、vy和vz分别为油箱辐射热量在x,y,z3个方向所产生的速度分量。

则变压器的动量守恒方程为

(18)

Tx、Ty、Tz为粘性损失项[11]；μ为动力粘度。

不可压缩流体的表达式为

(19)

Cp为油的比热容；T为油温；Qv为产生热量配件的体积。

通过k-ε模型减弱由于油的流动对温度场的影响。k-ε模型表示油在流动时产生的湍动能、能耗，具体表达式为

(20)

σk、σt为湍能和能量方程的施密特数[12]；μt为湍流粘度；g为热流密度函数；Φ为固体形状系数。计算出温度场中的各个能量变化后，即可掌握温度场中的温度分布特征情况，完成温度场分布的特征提取。

3 仿真实验

3.1 实验环境及变压器边界条件设定

实验在外界环境温度为20 ℃下进行。设置变压器自然冷却的边界条件为入口、出口的压力值为0。变压器油的相关参数如表1所示。

表1 油浸式变压器油物理参数表

随后给出实验目标的实际绕组流场分布以及内、外、辐向油道流速分布情况，如图1所示。

图1 变压器绕组流场分布

从图1a、图1b中可以看出，内轴流向油管中油的流速在初期会有增大的趋势，随后又以相同的幅度降低，外轴与内轴向的变化大致趋势相同，但是流速相对较快。分析图1c可知，绕组辐向油道流速分布较为不均匀，没有规律可言，这是由于管道宽度有所差异，一般情况下是以大、小相互间隔排列的，就导致了油的流速呈无规律状态。

3.2 提取结果分析

为验证本文方法是否能够准确提取出温度场的温度分布特征，以Fluent仿真软件为平台，通过流速以及变压器其他相关参数，计算出温度场中的各个能量变化。绕组的高压真实温度分布情况如图2a所示，通过本文方法进行特征提取后，获得变压器绕组的温度分布情况如图2b所示。

图2 高压绕组温度实际与本文分布对比

图2b右侧的色彩分布并不均匀，可知该变压器的线饼温度上升速度并不是匀速的，油流速较大区域的线饼温升较低，反之线饼的温升较高，这与图2a中描述出的变压器实际情况相符，提取结果和实际结果拟合程度高，证明了本文方法的有效性和准确性。

4 结束语

本文提出一种大型油浸式变压器绕组温度场分布特征提取方法。根据油浸式变压器的散热和发热情况，结合油的流动性完成变压器内部流体及固体的能量变化情况的分析，进一步推导出温度场的分布情况，实现温度场的分布特征提取。仿真实验表明，本文方法能够结合变压器各参数数据，准确地给出实验对象的温度分布情况，精准获得最高温度点，能够为变压器的运维提供参考依据，具有一定的实际应用价值。