功率二分支齿轮传动系统动载特性与模态分析

林 何，孟渔航，李瑞华，屈文宽

(1.西安工程大学机电工程学院，陕西 西安 710048；2.西安市现代智能纺织装备重点实验室，陕西 西安 710600)

0 引言

随着科学技术在航空和舰船等机械重工业领域的不断进步与发展，在该领域中，高精度、高承载和自动化等特点是目前的发展趋势，由于机械系统在传动运行过程中会产生振动，使轮齿动载荷加剧，降低系统工作可靠性，因此，研究机械齿轮系统的构型与动力学特性就显得尤为重要[1-2]。二分支齿轮传动系统作为现役直升机减速器系统中的一种重要构型，许多学者围绕该系统动态稳定性开展了相关研究[3-4]。Al-shyyab等[5]采用了集中质量法建立了直齿轮非线性动力学模型，构建了齿轮系统非线性微分方程，为不同构型齿轮动力学研究提供了建模思路；李润方等[6]通过对齿轮刚度、误差和啮合冲击典型动态激励源的数值模拟分析，得到该模型下的振动响应，该结果为分析复杂模型下动态激励源的振动响应提供了参考；蔡晓娜[7]以某直齿圆柱齿轮传动系统为研究对象，分析了该系统的动态响应，结果表明平稳的加载有利于齿轮传动系统动力的传递；高妍[8]研究了星型人字齿轮系统的固有频率与固有振型，讨论了机构参数对系统模态的影响；Cheng等[9]分析了准双曲面齿轮系统的共振特性，该研究结果为进一步分析其他构型的齿轮系统模态、动载荷系数、啮合振动位移、动态啮合力和啮合频率条件下系统振动特性具有启发意义。

本文通过建立由斜齿分扭传动级与人字齿并车传动级构成的纯扭转动力学模型，采用高斯消元法消除了动力学方程组中存在的冗余变量，并使用Runge-Kutta法进行数值求解，分析了斜齿与人字齿齿型所构成的2级传动动载特性，采用模态分析法确定该系统的固有频率与固有振型，结合三维瀑布图分析了激振频率对振动系统的主谐波阶次与共振特性影响。

1 系统动力学模型与方程

二分支齿轮传动系统结构如图1所示，该系统主要由功率输入轴上斜齿轮1与斜齿轮2、3啮合传动构成第1级分扭传动级，其中，轮齿啮合副可表示为Me1；通过斜齿轮4(5)与斜齿轮6，斜齿轮7(8)与斜齿轮9啮合传动构成第2级并车传动级功率输出，人字齿轮构成的并车传动级均视为由2个斜齿轮4、7，斜齿轮5、8与斜齿轮6、9组合而成，该啮合齿轮副可表示为Me2，将其连接组合处视为欧拉伯努利梁单元。

图1 二分支齿轮传动系统

采用质量集中法构建分扭-并车齿轮传动系统纯扭振动模型，如图2所示。构建动力学模型时考虑了传动系统的质量、阻尼与弹性元件3要素；各级齿轮啮合处通过可储存势能的弹性元器件弹簧与消耗系统能量的阻尼器连接，人字齿轮组合处视作弹簧阻尼器连接，模型中Ti为输入功率，To为输出功率,ri(i=1,2,…,9)为各齿轮基圆半径，θi(i=1,2,…,9)为各单元相对扭转角位移，弹簧ki与阻尼器ci(i=1,2,5,6,9,10)分别为系统各轮齿的啮合刚度、啮合阻尼；其中，k3(k4)和c3(c4)为扭转轴处扭转刚度与扭转阻尼，k7(k8,k11)和c7(c8,c11)为人字齿轮所分斜齿轮4 (5,6)与斜齿轮7 (8,9)梁单元的扭转刚度与扭转阻尼，设各轮齿扭转角θi(i=1,2,…,9)方向如图2所示为正方向，该系统主要动力学参数如表1所示。

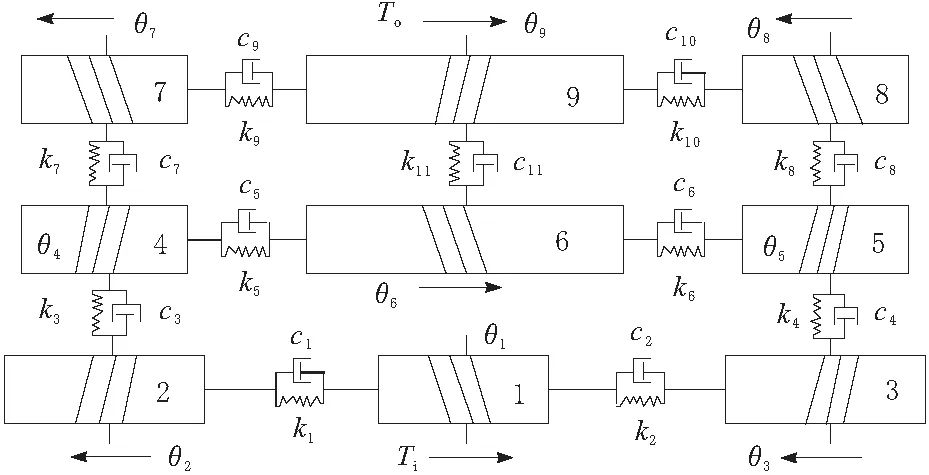
图2 二分支齿轮传动系统纯扭振动模型

表1 二分支齿轮传动系统主要动力学参数

根据牛顿第二运动定律构建系统动力学方程为

(1)

根据式(1)系统扭转自由振动方程可以表示为

(2)

I为机构齿轮转动惯量矩阵；θ为系统振型矩阵；K为动力学系统的刚度矩阵。

该系统轮齿相对啮合线位移为

(3)

该系统轮齿相对扭转角位移为

(4)

由于系统啮合振动相对线位移和相对扭转角位移变量与系统动力学方程阶数不一致,会使动力学方程线性相关,在此，构建增广矩阵并采用高斯消元法使动力学方程组线性无关,为后续动力学方程无量纲化及状态方程数值求解提供研究对象。

有关溶解纤维素以制备5-羟甲基糠醛(5-HMF)的研究已进行将近一个世纪，国内外研究者利用不同的溶剂对纤维素进行溶解，提出了众多的宏观和微观的反应动力学机理。本文对单一有机溶剂、离子液体、混合溶剂和水4个热点溶剂溶解纤维素催化转化制备5-HMF的机理和优缺点进行了综述，图6展示了全文词汇出现的频率，除纤维素、溶解、溶剂之外，5-HMF、催化剂、溶度共熔溶剂(DES)等词出现的频率最高，在此也针对这几个对象对未来的工作提出一些展望。

根据式(3)与式(4)构建非齐次线性微分方程为

P·Θ=x

(5)

P为变换矩阵；Θ为相对扭转角位移量；x为相对啮合线位移矢量，展开为

(6)

(7)

(8)

M为单位质量矩阵；K、C分别为动力学系统无量纲化后的刚度、阻尼矩阵；F为系统外载荷矢量；f(x,τ)为无量纲化后的非线性函数。

在载荷波动及内、外激励因素作用下，各级齿轮啮合副的啮合特性呈现出动态波动特性，故为研究该动载特性，引入动载系数kv来衡量动力学参数的变化对系统振动的影响。动载系数kv的计算公式为

(9)

将时变啮合刚度k(t)以傅里叶级数展开为

(10)

最后使用Runge-Kutta法对无量纲化动力学微分方程数值求解。

2 动力学分析

2.1 动载特性

图3表明齿轮传动系统第1级斜齿分扭级啮合副Me1在无量纲时间变化下，传动系统的动载特性与无量纲位移；在输入转矩T=1 000 N·m与转速n=4 000 r/min时,分扭传动级啮合副Me1处的动载系数kv在无量纲时间t∈[0,45.6]区间内剧烈波动,动载系数kv最高激增至3.06,此时该系统未进入稳态，而在t∈[72.3,500]区间时,系统动载系数与无量纲位移分别稳定于1.67与1.64且均呈周期性波动逐渐收敛进入稳态。

图4为该齿轮传动系统第2级人字齿并车级啮合副Me2在无量纲时间变化下的动载特性与振动位移；在相同输入转矩与转速的情况下，并车传动级啮合副Me2处动载系数kv与无量纲位移均在t∈[0,84.8]区间内剧烈波动，且动载系数kv最高激增至2.35，而无量纲位移跃升至2.52，在该区间系统并未进入稳态，但在t∈[92.15,500]区间时,此时系统动载系数kv与啮合振动位移为1.42且均呈周期性波动收敛进入稳态，由于人字齿由于不受径向力影响，随着无量纲时间的变化，系统动载系数与无量纲位移相较斜齿分扭级在时间历程内的波动相对较为平缓，不易出现系统振动加剧的状况。综合考量，该系统第2级人字齿并车级动力学特性要优于第1级斜齿分扭级传动。

图3 分扭传动级动载系数与振动位移

图4 并车级动载系数与振动位移

2.2 模态与共振分析

根据动力学方程式(2)，以纯扭转动力学模型为基础，将系统上轮齿啮合副与梁单元上连续的质量集中为9个节点，通过纵坐标振幅系数η来表示横坐标对应节点i的振幅ηi(i=1,2,…,9)，对系统的固有频率ωn与模态振型的变化进行分析，在固有频率ωn的求解过程中，由于系统共有9个自由度，故每个固有频率均对应1阶主振型，解得系统的固有频率ωn分别为：0、72.4 Hz、81.3 Hz、129.7 Hz、129.7 Hz、309.3 Hz、313.5 Hz、656.7 Hz、656.7 Hz。

从图5系统九阶模态振型中可以看出,各构件在不同固有频率下呈现出的扭转振动振型，从得到的固有频率数据中看，第1阶固有频率为0是由于系统扭转方向未被约束而存在刚体位移，即可以自由转动；而二分支齿轮传动结构又具有对称性，故第4阶与第5阶、第8阶与第9阶固有频率均产生了重频现象且模态振型也较为相似。

对系统转速与频率下的稳态响应进行傅里叶变换，得到系统无量纲位移(图6)与动态啮合力(图7)瀑布图，反映时变转速下主谐波阶次与系统的共振特性；在图6与图7系统转速4 000 r/min条件下，均由一阶主谐波最大波峰反映系统主要振动特征，且在该系统激振频率为1 820 Hz时，产生振幅较大的超谐波共振，其产生的谐波共振线与激振频率轴垂直使得系统结构内部应力集中，故在设计运行中系统的激振频率需远离该数值避免激发共振。

图5 系统九阶模态振型

图6 无量纲位移频率转速瀑布图

图7 动态啮合力转速频率瀑布图

3 结束语

本文构建了功率二分支齿轮传动系统纯扭转动力学模型，采用高斯消元法消除多自由度振动方程组所含的冗余变量，解决了多变量数值求解过程中系统刚度矩阵奇异性问题。通过研究该机构的动态载荷发现，分扭级变化相较并车级较为剧烈且两级传动中动载荷系数与无量纲位移均在进入稳态后呈周期性规律波动。通过对系统的模态分析并结合瀑布图探究了系统的共振行为， 结果表明该系统在激振频率为1 820 Hz时，会产生超谐波共振。本文的研究结果为系统因谐波频率不当而激发共振的问题提供了解决思路。