基于粒子群算法的大棚温度自适应离散模糊控制系统

王铁广，王明华，丁锐，李文勤，邢凯，李明

（西南林业大学机械与交通学院，昆明 650224）

0 引言

我国作为农业大国，大棚的应用广泛。在大棚系统正常运行的过程中，温度控制是一项影响农作物品质和产量的关键性制约因素。采用传统的控制方法、控制理论完成温度控制过程需要建立大棚内部温度模型，影响大棚温度的因素众多，精确的数学模型难以获得，因此无法达到较好的控制效果[1]。模糊控制系统可以在不需预先建立精确数学模型的情况下根据实际数据并参考工作人员的经验完成温度的有效调节[2]。但其调节过程过度依赖专家经验，一般情况下，很难在保证系统稳定的前提下，达到快速响应的目的。粒子群算法（PSO）是一种智能的寻优工具，具有收敛速度快、控制精度高等优点[3]，在非线性时变系统的控制调节方面表现出强大的潜力。

为此，研究将模糊控制与PSO相结合，提出一种基于PSO的大棚温度模糊控制系统。采用ITAE准则为目标函数，并利用PSO获取模糊控制需要的量化因子和输出比例因子；同时采用带离线计算、在线查表的模糊控制系统充分降低系统的运算量，以实现温控系统快速响应和平稳运行的目的。

1 大棚温度模糊控制系统

根据大棚温度的控制特点，本文采用粒子群算法对控制过程中的量化因子和输出比例因子进行寻优，目的是在模糊化、反模糊化过程中在设定的搜索范围内确定量化因子和输出比例因子最优值，从而解决设定参数过度依赖经验规律的问题。粒子群算法优化模糊控制系统控制过程如图1所示。

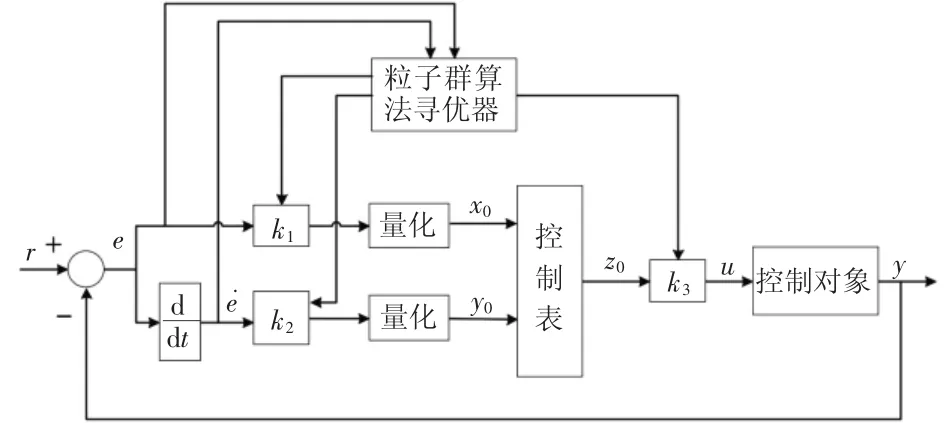
图1 粒子群算法优化的模糊控制系统结构图

1.1 模糊控制器结构设计

本文根据模糊控制系统的基本结构设计了一种离线计算、在线查表的模糊控制系统（如图2）。在离线模糊计算部分，温度检测系统反馈给控制系统的温度值均为整数，且大棚内温度的变化为±6 ℃，所以输入量温度偏差Te和偏差的变化率Te˙的值是有限的。此时输入量x0、y0的个数有限，不同x0、y0的组合经过模糊化、模糊推理和清晰化计算形成一张控制表。在线查表过程中，系统会根据输入的Te值和Te˙值，查询控制表得到相应的输出控制量Z0，输出控制量Z0乘以输出比例因子得到最终输出控制量。此模糊系统能够满足实时控制的要求，能够较好地完成大棚温度的控制任务。

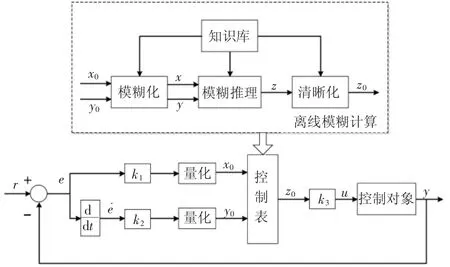
图2 模糊控制系统结构

1.2 输入、输出变量确定

式中，Ts为采样时间。

1.3 输入、输出量的模糊化处理

根据温度偏差Te的计算结果可以进行模糊化处理，得到模糊推理所需数值。通过对大棚的温度测量统计分析，大棚温度偏差Te的变化范围为[-6,6]；大棚温度偏差变化率Te˙的变化范围为[-1,1]；输出控制量Z0的变化范围为[0,12]。

大棚温度偏差Te与大棚温度偏差变化率Te˙的模糊论域为

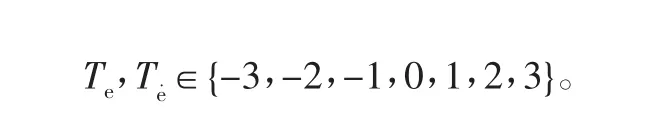
输出控制量Z0的模糊论域为

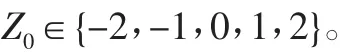
大棚温度偏差Te与大棚温度偏差变化率Te˙的模糊集合为{NB,NM,NS,ZE,PS,PM,PB}，输出控制量Z0的模糊集合为{NB,NS,ZE,PS,PB}大棚温度偏差Te、大棚温度偏差变化率Te˙及输出控制量Z0需要进行相应的论域变化，三者通过温度偏差量化因子k1、温度偏差变化率量化因子k2和输出控制量比例因子k3完成各自的论域变化。根据文献[4]，得到误差量化因子、变化量化因子及输出比例因子计算公式。

1.4 语言变量的隶属度确定

用正态函数来描述模糊变量是最合适的[5]。大棚温度偏差Te、大棚温度偏差变化率Te˙及输出控制量Z0模糊集合的隶属度函数图像如图3、图4所示。

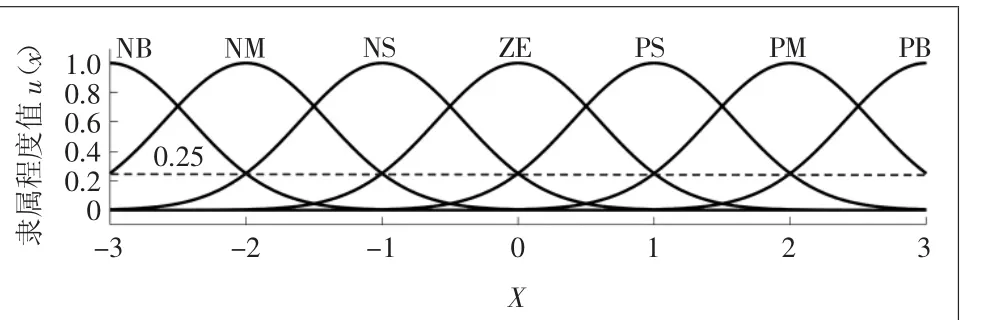
图3 大棚温度偏差Te、大棚温度偏差变化率Te˙隶属度函数图像

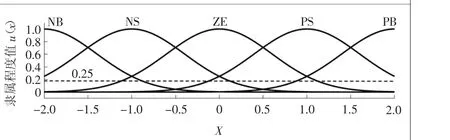
图4 输出控制量Z0隶属度函数图像

将大棚温度偏差Te、大棚温度偏差变化率Te˙及输出控制量Z0对应的隶属度函数以矢量形式表示，如表1、表2所示。

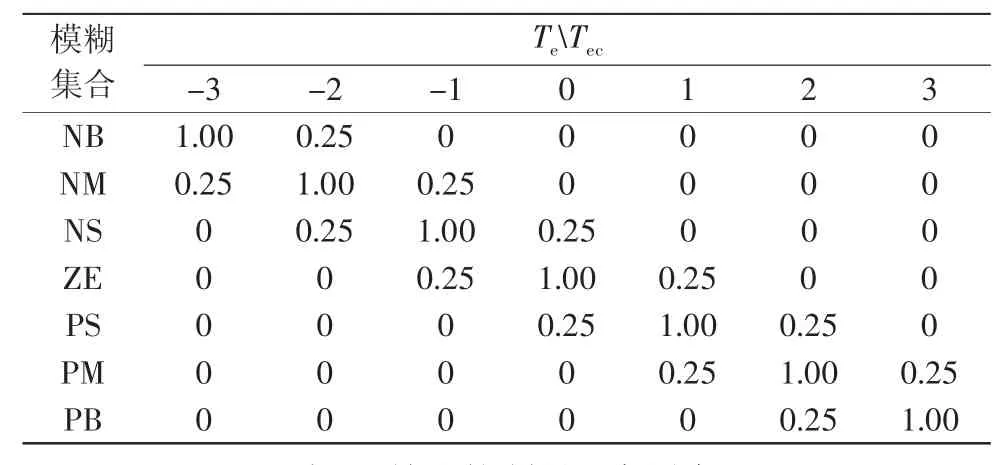
表1 大棚温度偏差Te、大棚温度偏差变化率Te˙隶属度

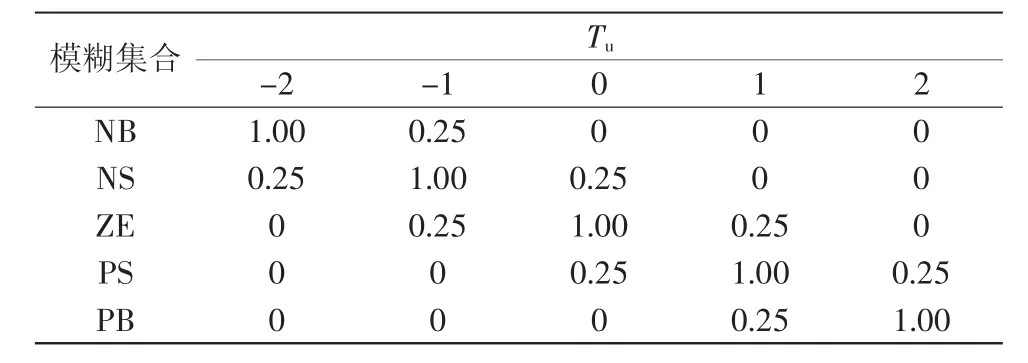
表2 输出控制量Z0隶属度

1.5 模糊控制规则的确定

在大棚温度的调节过程中，根据日常大棚调节温度操作经验，总结出相应的控制规律，并用推理语句进行表示。同时，大棚温度偏差Te、大棚温度偏差变化率Te˙的模糊分割数均为7，所以模糊控制表包含49条控制规则，如表3所示。

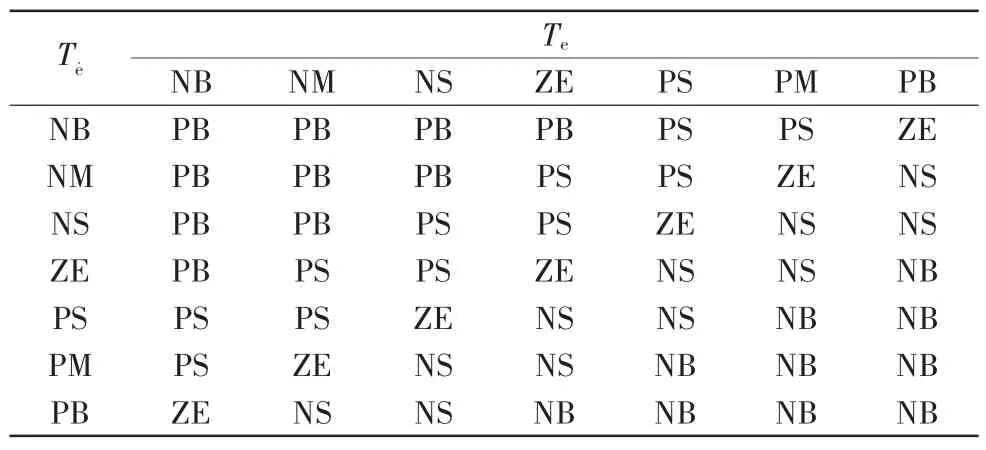
表3 模糊控制规则

1.6 模糊推理

由模糊控制规则可知模糊条件语句使用“and”进行连接，这种推理方式为：如果x是A and y是B，则z是C。本文中x是大棚温度偏差Te，y是大棚温度偏差变化率Te˙，z是输出控制量Z0。模糊前提“x是A，则y是B”可以看成直积空间X×Y上的模糊集合，并记为A×B,其隶属函数为

式中：R为模糊蕴含关系；“°”为合成运算符。

1.7 清晰化处理

通过模糊推理得到的是模糊量，在实际的模糊控制系统中要求最终给执行机构的是精确量，所以需要将模糊量转变为精确量。采用加权平均法进行模糊量的清晰化计算[6]，经过清晰化后所得值如表4所示。

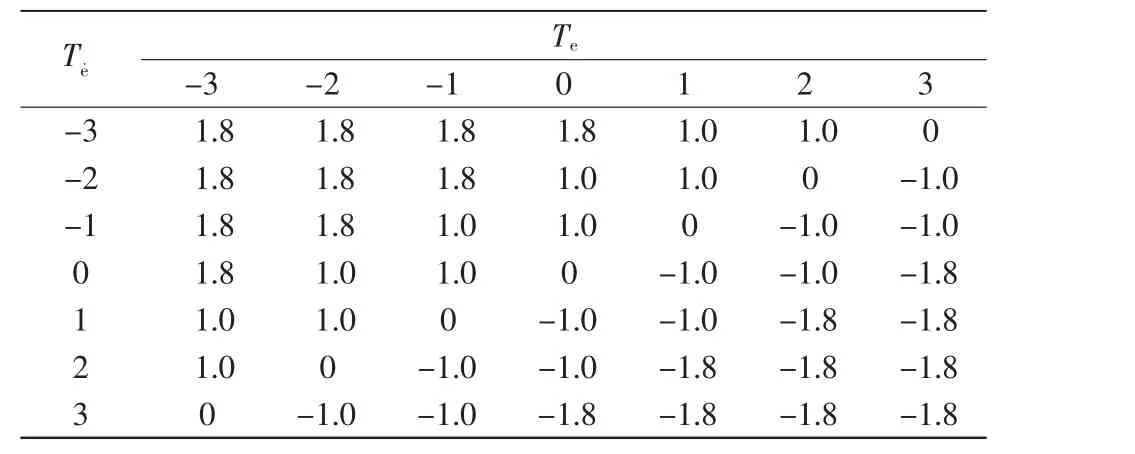
表4 控制表

2 引入粒子群算法的因子优化

粒子群优化算法（PSO）是一种仿生优化方法[7]。每个待优化的问题模仿鸟群中的个体在搜索空间内飞行，鸟群中的个体被称为“粒子”。每个粒子的适应值由目标函数决定，粒子根据个体飞行与群体飞行经验调整飞行速度和位置[8]。

在任意t+1时刻，粒子群中第i个粒子第j维的速度和位置更新方程[9]为：

本文通过粒子群算法对模糊控制器的量化因子和输出比例因子进行寻优。量化因子k1、k2的值影响控制系统的动态性能，较大的k1值会造成系统大的超调及较长的过渡过程。较大的k2值会减小超调量，但会减慢系统的响应速度。输出比例因子k3选择过小使得系统的动态响应变慢，选择过大会使得系统出现振荡。为了获取最优的量化因子和输出比例因子，以积分性能指标（ITAE）作为寻优目标函数，ITAE性功能指标的实用性和选择性较好，可以很好地评价系统的动态性能和稳态性能。ITAE公式表示为

粒子群优化算法的优化流程如下：

Step1:初始化粒子种群。根据优化参数个数设置搜索维度为3，初始粒子30个，更新迭代次数为50次；惯性权重和加速因子是影响粒子群算法优化性能的重要参数[10]，为了使得粒子群优化算法性能最优，根据文献[10]采用ω=0.68，c1在迭代过程中由2.5线性减小到0.5，c2由0.5线性增加到2.5。

Step2:进行适应度计算。将每个粒子的位置作为待优化因子的参数值，通过ITAE积分性能指标，计算各个粒子的适应值，更新pbest和gbest的值。

Step3:根据式（13）和（14）调整粒子当前的位置和速度。

Step4:检查算法终止。若迭代次数达到上限或者得到最优适应值，程序终止；否则，转至Step2继续寻优。

3 仿真试验与结果分析

3.1 建立控制对象数学模型

大棚白天温度保持在25 ℃适宜植物生长[11]，为了准确建立大棚温度变化数学模型，加强对大棚温度的有效控制。此次温度数据采集于实验大棚，实验大棚尺寸数据为：跨度为4 m、肩高为1.6 m、脊高为2.5 m、长度为8 m。通过对大棚白天某时段调节升温过程中的温度进行采集，得到大棚温度变化拟合曲线的温度数据。此次采集间隔时间为90 s，对大棚内6个采集点进行温度采集，并计算这6点温度平均值作为大棚温度变化拟合曲线的温度数据。大棚温度变化拟合曲线如图5所示。

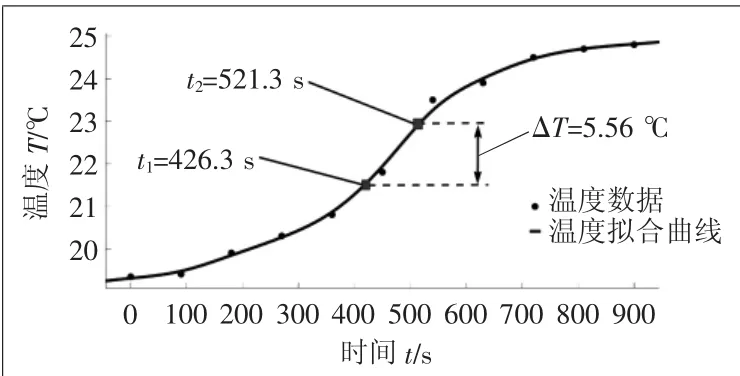
图5 大棚温度变化拟合曲线

为更好地描述大棚温度的动态特性，大棚的控制数学模型[12]可表示为

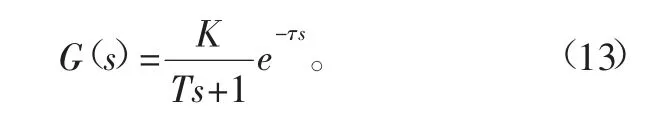
式中：K为大棚温度的放大系数；T为时间常数；τ为滞后时间。

利用两点法[13]计算被控对象的传递函数，分别在调节温度变化的39%、64%时记录时间t1、t2，ΔT=5.56 ℃。具体计算过程如式下：

3.2 仿真结果分析

基于粒子群算法的大棚温度自适应模糊控制系统，具体仿真过程分为模糊控制器的Simulink框图搭建（如图6），以及构建.m文件通过粒子群算法进行因子优化，完成控制系统的仿真。

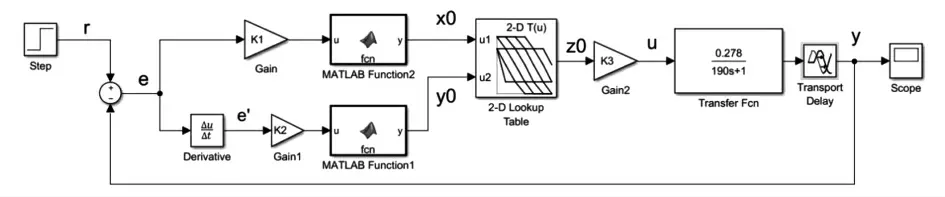
图6 模糊控制器Simulink仿真框图

模糊控制器Simulink仿真框图中MATLAB Function模块应用四舍五入round函数；Look-Up Table(2-D)中的值根据表1～表4填写；Transfer-Fcn与Transport-Delay模块根据式（18）进行设置；量化因子k1和k2、输出比例因子k3的值根据基本公式粗略计算值和粒子群算法寻优值进行设置，并完成对比仿真实验。

通过MATLAB程序对大棚温度偏差量化因子k1、大棚温度偏差变化率量化因子k2和输出控制量比例因子k3进行寻优得到k1′=3.45，k2′=1.8，k3′=2；与基本公式得出的k1=0.5, k2=3, k3=2，同时放入Simulink中进行仿真，得到控制系统响应曲线的对比，如图7所示。

根据图7可以得出，经过粒子群算法优化的模糊控制器比普通模糊控制器阶跃响应达到稳态的时间缩短了46.3%；响应曲线的延时时间由温控系统的自身特性决定；优化后的模糊控制器响应曲线无法做到完全平滑，是粒子群算法优化因子所起作用。综合对比，经过粒子群算法优化的模糊控制器拥有最佳的控制效果。

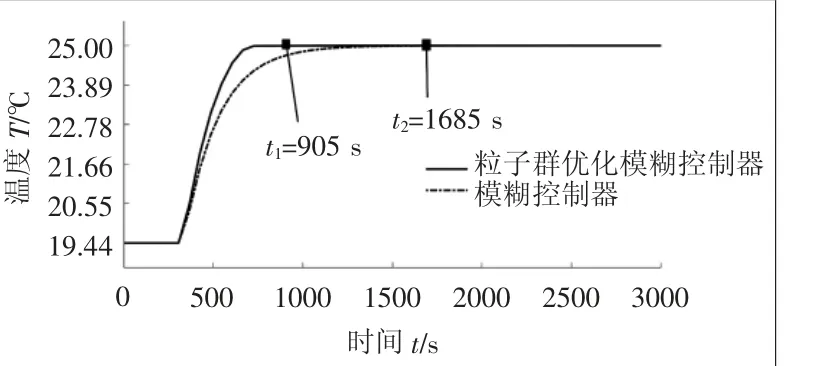
图7 控制系统响应曲线

4 结论

本文针对大棚温度控制策略问题，建立大棚离散模糊控制系统，满足模糊控制系统的实时控制性要求，在此基础之上引入粒子群算法对离散模糊控制系统进行优化，提高控制系统的自适应性，更好地完成对大棚温度的控制。通过仿真实验对比，基于粒子群算法的大棚自适应离散模糊控制系统取得良好的控制效果，此方法可以在相关领域推广应用。