基于响应面模型的清淤射流泵吸头参数优化设计
2022-03-24倪其军阮文权
倪其军,阮文权
(1.江南大学,江苏 无锡 214122;2.中国船舶科学研究中心,江苏 无锡 214082)
0 引 言
清淤射流泵是一种依靠一定压力的工作流体来传递能量和质量的流体输送机械,工作泵从清水源吸入清水经加压后通过工作水管输送至射流器,产生的高速射流(工作流体)通过喷嘴进入接受室,此时喷嘴附近会形成一个低压区将附近的介质(表层沉积物)吸走,工作流体和被吸入的流体(引射流体)混合充分后输出,从而达到了高效清淤的目的。射流泵内部无运动部件,可有效防止淤泥扩散造成对水体的二次污染。清淤射流泵结构参数以及内部流体流动特性对其性能具有直接影响[1],已成为该领域的研究重点。
目前,国内外众多学者利用实验或数值模拟计算的方法对不同类型的射流泵内部流动特征进行研究,并取得了一些成果。高贵军[2]基于CFD技术对不同的液气射流泵喉嘴腔收缩半角进行了三维数值计算,分析了喉嘴腔收缩半角对液气射流泵内部流场情况的影响关系;Senthil[3]的研究认为喷嘴距大致在1~1.7 倍喷嘴直径时,可取得较好的效率;Shah[4]通过试验研究射流泵流场特性,分析主要结构参数与泵性能之间的关系,发现在高速射流与低速入流混合段存在较大能量耗散;高全杰[5]将环形射流泵和自激振荡射流的优势相结合提出了一种新型射流泵,通过数值模拟的方法研究了不同流量比工况下新型射流泵的性能和效率,以及流场内部流动参数的变化规律;Shimizu[6]通过大量实验初步研究了射流泵结构参数对其空化性能的影响。以上研究主要采用数值模拟方法研究各类射流泵的内部流动,以及主要参数对其性能的影响分析。
近年来许多学者在数值模拟射流泵流动特性的基础上,开始采用试验设计(Design of Experiment,DOE)与响应面模型(Response Surface Model,RSM)等方法,开展射流泵结构参数的优化设计工作,并取得了一些研究成果。王春林[7]将正交试验方法应用于流体机械结构优化,提升了性能;王常斌等[8]基于数值模拟对泵内流场进行分析,总结了射流泵最优参数的确定方法;Eames[9]对射流泵的能量交换原理进行了研究,提出了高性能射流泵的设计方法;肖龙舟[10]从吸入室角度、喉嘴距、喉管长度等多方面对射流泵做了深入研究,确定了较优结构参数,以提高其效率;刘军[11]利用软件拓扑优化模块确定优化参数,建立响应面模型,应用多目标遗传优化算法进行了优化设计;高学平[12]以扩散段体型参数为设计变量,以进/出流各水力指标作为优化目标,利用响应面法建立了两者之间的代理模型,利用NSGA-Ⅱ遗传算法进行了多目标优化,得到最优体型。综上所述,以CFD 作为分析工具,结合响应面模型,开展结构参数优化已成为射流泵性能最优设计的一种可行途径。
作者在文献[1]中采用CFD技术数值模拟了射流清淤泵内流场,分析了射流泵内的流体流动机理,给出了影响射流泵清淤效果的主要参数。本文在此基础上,以射流泵性能最优为目标驱动,采用响应面模型方法开展基于CFD数值模拟技术的射流泵主要参数优化设计。首先以数值计算方法作为射流泵性能评估的工具,采用试验设计方法对射流泵的设计参数与其性能影响关系进行了分析。之后,建立响应面模型,利用优化算法对该优化设计问题进行求解,获得最优设计方案。
1 清淤射流泵的原理与性能评估
1.1 清淤射流泵的基本原理
目前,不管是绞吸式、耙吸式还是其他一些式样的水下吸泥装置均依靠进口处的低压吸入淤泥,因此其吸泥能力以及对淤泥的搅拌能力均受到了进口速度的限制。通常进口速度不足以将淤泥冲刷掉,需要特定的旋转盘或者高速射流来辅助,而这些操作大多会导致淤泥在水体中的扩散。本文利用流体力学Coanda效应,可以避免使用机械旋转部件,有效防止清淤过程中淤泥扩散对水体造成的二次污染。流体力学Coanda 效应(图1)就是沿切于壁面方向或者近于切向,向外喷射流体,流体将贴着其附近的固体壁面而流动。利用Coanda 效应,研制一种新的射流吸泥装置如图1 所示。它是个轴对称装置,包括出口管、扩散段、混合腔、掺混区、高压分配腔、进口管以及两道射流喷口。
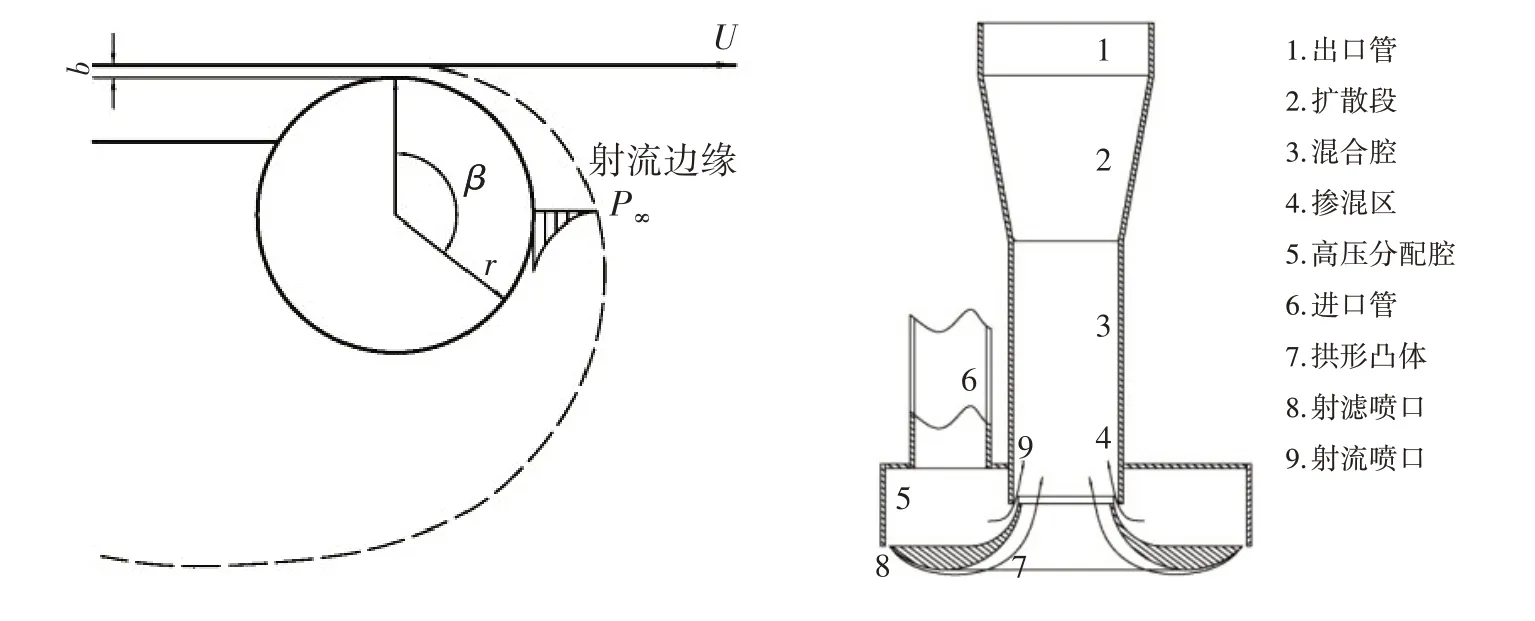
图1 Coanda效应与清淤射流泵原理图Fig.1 Schematic diagram of Coanda effect and jet pump
清淤射流泵的基本原理:水泵通过进口管将水输入高压分配腔,进行水的分配,提供给两个射流喷口,从而产生两道射流。底部喷口形成高速射流,根据流体力学的Coanda 效应,流体将沿着拱形凸体流动,而不发生分离,该射流的作用主要是粉碎底泥形成泥浆。上部喷口同样形成高速射流,从而卷吸下面的低压流体,在掺混区内产生质量能量交换,最后形成流速均匀的混合流体,通过扩散段由出口管输出,实现清淤。
1.2 清淤射流泵吸头性能评估
清淤射流泵是安装在清淤船上用来清除河流底部淤泥的装置。三维射流泵可以简化成二维的轴对称结构,如图2 所示。其中有2 个间隙,分别为上喷口间隙和下喷口间隙。给定进口一个压力值,水在高压泵的作用下流向底部并从两个狭小的间隙处喷出,下喷口的射流对淤泥进行扰动,并由上喷口射流的低压及流速将淤泥浆吸入泵中心出口管道,最终从输出口输出淤泥,完成清淤。
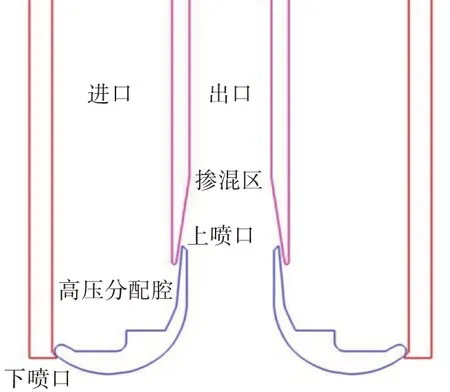
图2 射流泵二维剖面示意图Fig.2 Two-dimensional profile of jet pump
本文采用RANS 方程对清淤射流泵内部的流场进行数值求解。选择RNGk-ε湍流模型,动量方程采用有限体积法(FVM)进行离散。对流项采用二阶迎风差分格式,扩散项采用中心差分格式。选用流场中经典的SIMPLE(Semi-Implicit Method for Pressure-Linked Equations)算法处理压力速度耦合问题。详细数值方法及网格划分可参考文献[1]。清淤射流泵性能即清淤效能采用射流泵对底部冲刷的动量QhVh(泥水流量与底部剖面速度的乘积)和有效作业效率η来表征。
2 射流泵吸头参数优化设计
文献[1]采用数值计算方法模拟了射流清淤泵内流场,分析了射流泵内的流体流动机理,给出了影响射流泵清淤效果的主要参数。本文选择上下喷口间隙、出口半径、底部距离四个参数,应用响应面方法建立参数与其性能之间的关系,并利用优化算法对最优设计问题进行求解,获得性能最优的射流泵参数设计方案。
2.1 清淤射流泵吸头参数优化设计方法
(1)优化设计流程
采用响应面模型的射流泵吸头参数优化设计的具体流程如下:(1)在给定的参数范围内,采用优化拉丁方设计,建立设计方案参数表,定义各射流泵吸头构型方案;(2)利用数值评估方法计算各方案性能,并进行设计参数敏感性分析;(3)建立敏感参数与设计目标之间的响应面模型,获得参数与目标之间的关系式;(4)在此基础上,依据给定的约束条件,利用优化算法进行求解,获得最优解与相应设计参数;(5)对优化方案性能进行数值计算,验证优化方案的可靠性。
(2)试验设计法
试验设计法是数理统计的应用之一,它能够考虑参数间的交互作用,通过合理地安排试验,以求通过较小的试验次数得出参数与响应间的关系,从而提高优化效率。本文采用的试验设计法为优化拉丁方设计,该方法易在各因子取值范围内获得精确的拟合模型。
(3)响应面模型
响应面方法用于对受多变量影响的问题进行建模与分析。采用多元回归方程拟合变量和响应值之间的函数关系,为多变量优化问题提供指导。
2.2 试验设计方案与结果
应用优化拉丁方试验设计方法,对四个设计参数在其设计范围内划分不同的水平,共20 个方案如表1所示。表2给出了20个方案的数值计算结果。
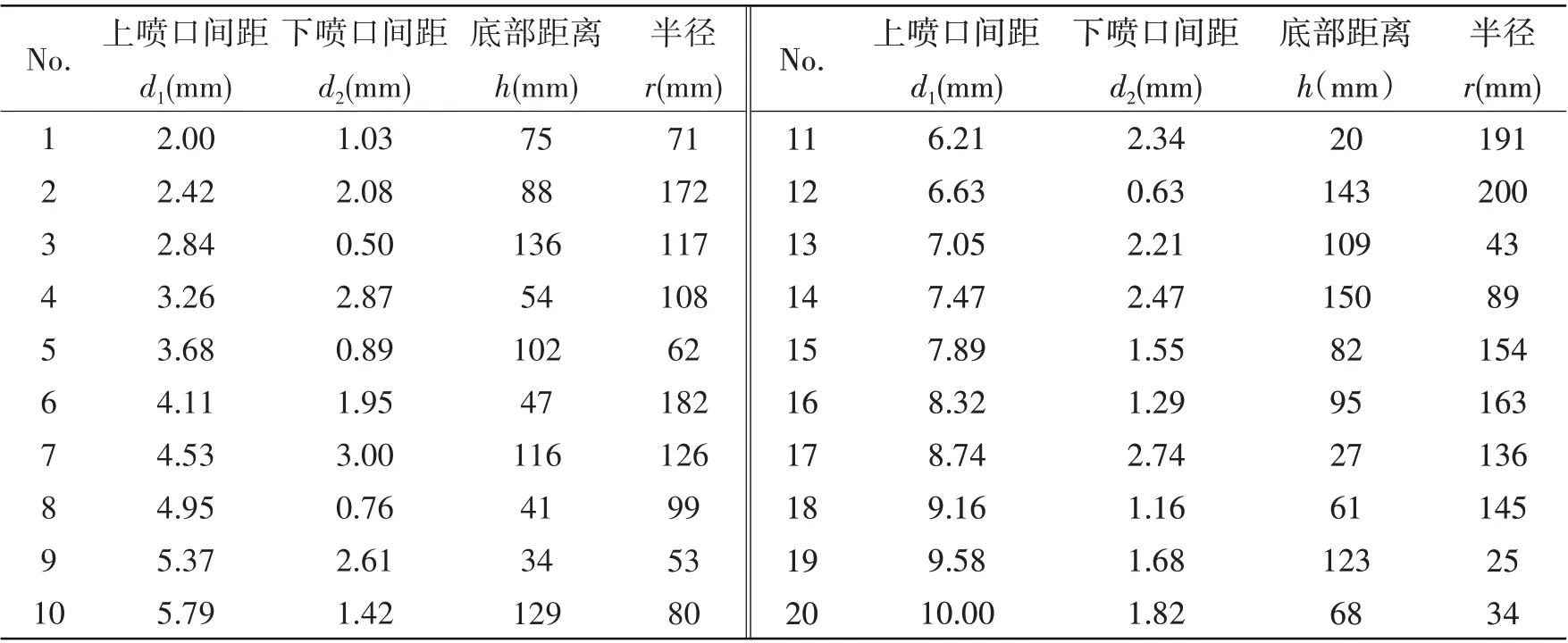
表1 射流泵各方案设计参数尺寸Tab.1 Main parameters of jet pump cases
从表2可以看出,不同设计方案的作业效率差别非常大:No.6的作业效率最高,为28.7%,No.13的作业效率最小,为0.8%。出口总流量同样差别较大:No.12最大,为3584.9 m3/h;No.1最小,为394.2 m3/h。出口总流量和作业效率未成对应关系。QhVh最大时对应的方案是No.6,为8.7 m4/s2,最小对应方案是No.13,为0.1 m4/s2。作业效率和底部泥水冲量最大的方案相同,均为No.6。
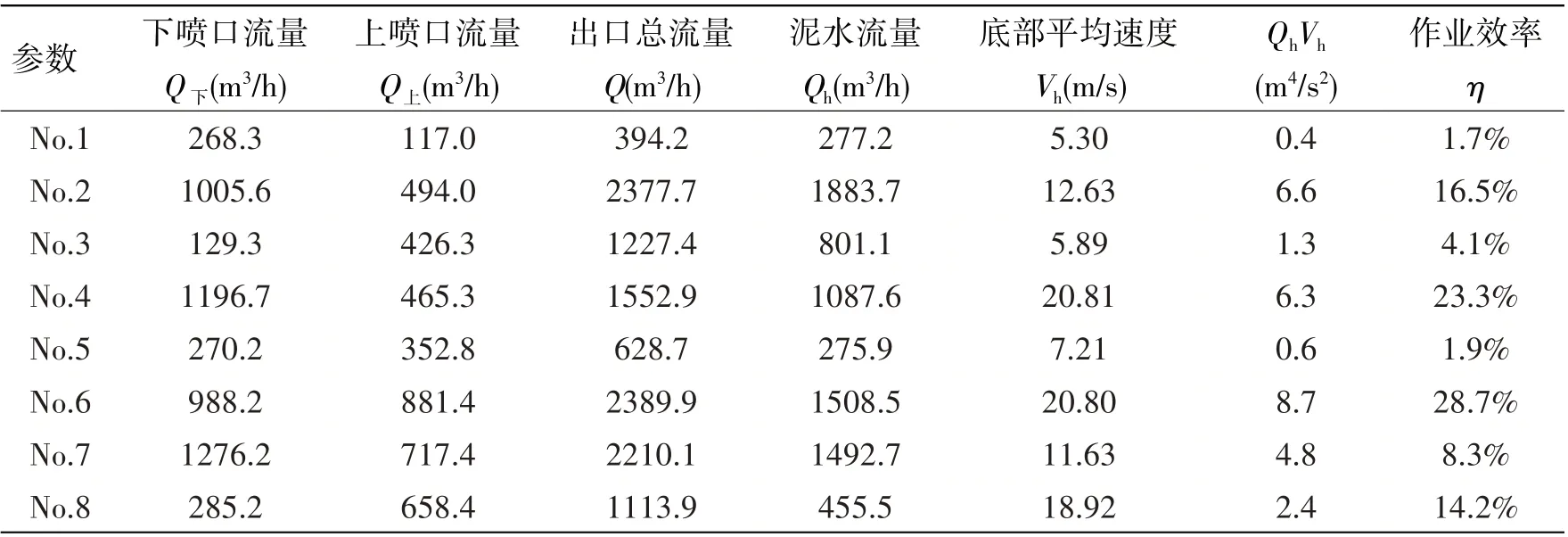
表2 各方案主要参数(流速和流量)的计算结果(P=12 atm)Tab.2 Main parameters(flow velocity and flow rate)of cases at P=12 atm
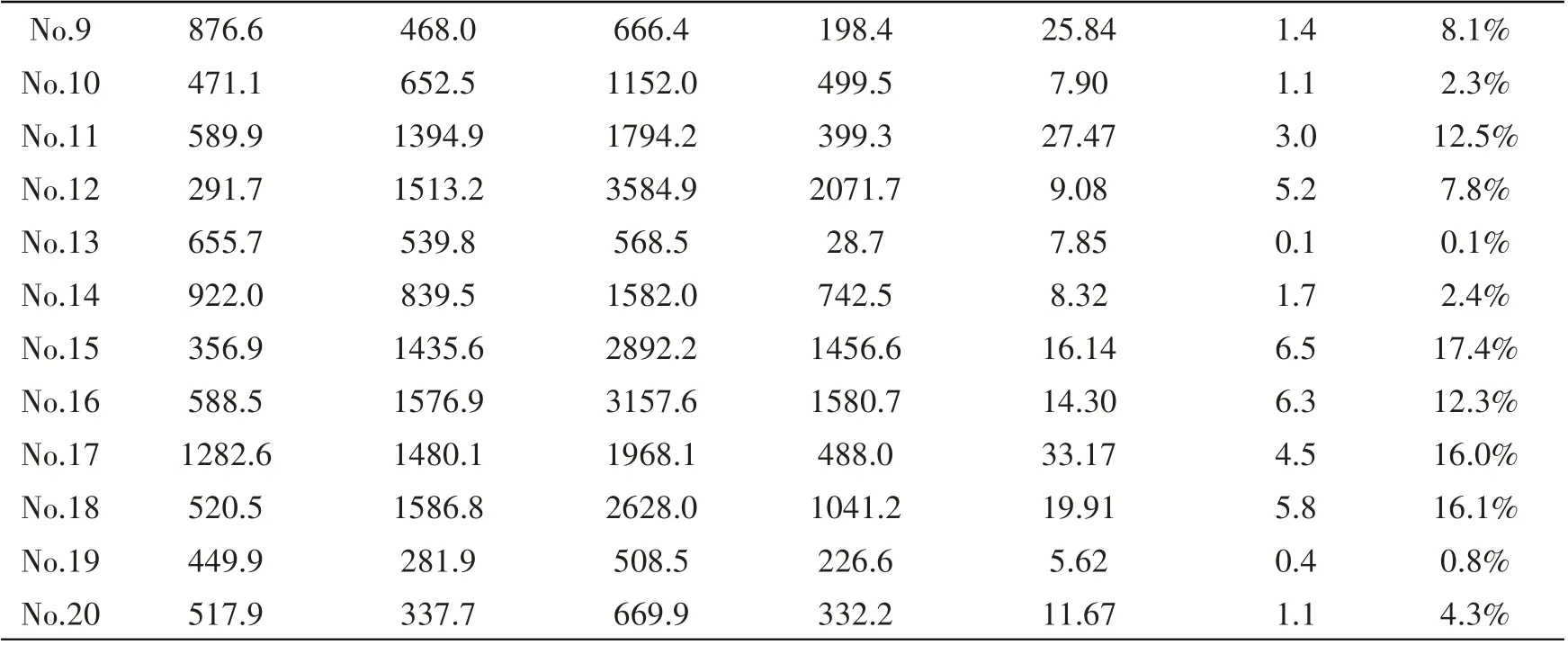
续(表2)
为了解设计参数对出口总流量、底部淤泥的冲量、作业效率等的影响大小以及影响规律,需要进一步对设计参数进行敏感度分析,以及建立底部淤泥的冲量、作业效率等参数的响应面模型。
2.3 设计参数敏感度分析与性能的响应面模型
为了从中确定影响较大的因素,分析了设计参数对底部冲刷动量与作业效率的影响规律。根据各方案计算结果,图3给出了四个参数的一次项、交互项与二次项对底部冲刷动量的贡献度,图4给出了四个参数的一次项、交互项与二次项对作业效率的贡献度。
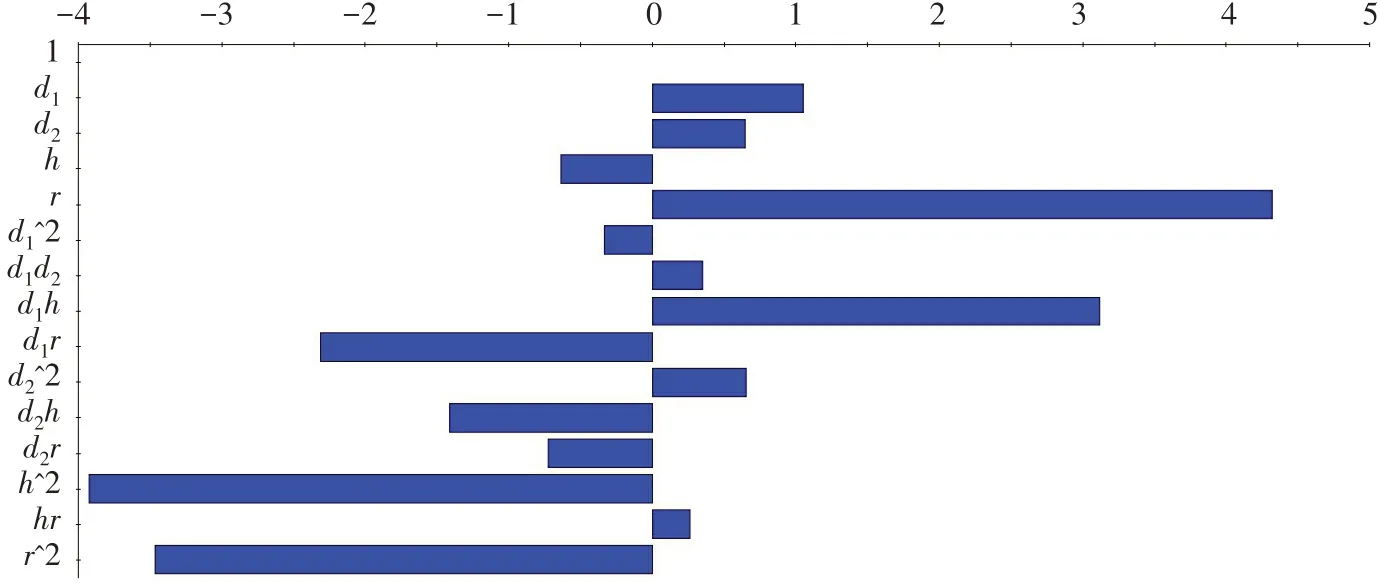
图3 四个参数的一次项、交互项与二次项对底部冲刷动量的贡献度Fig.3 Contribution of primary term,interaction term and secondary term of four parameters to bottom scour momentum
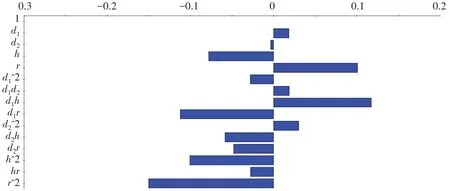
图4 四个参数的一次项、交互项与二次项对作业效率的贡献度Fig.4 Contribution of primary term,interactive term and secondary term of four parameters to operation efficiency
对试验次数不够多的设计来说,拟合项过多,可能引起拟合结果失真,适当减少拟合项的数量,可使拟合方程更加有效。对图4和图5中四个参数的一次项、交互项及二次项的贡献度进行分析可以看出,四个参数的一次项中r对底部冲刷动量的贡献度最大,其它三个参数相当;二次项中,d1h、d1r、d2h、h2、r2对底部冲刷动量的贡献度较大,d12、d1d2、hr则较小。
四个参数的一次项中h和r对作业效率的贡献度较大,d1次之,d2最小;二次项中,d1h、d1r、d2h、d2r、h2、r2对作业效率的贡献度较大,d12、d1d2、d22、hr则较小。
从参数实际代表的意义出发,底部距离h和出口半径r对底部冲刷动量和作业效率影响较大。四个参数间的耦合效应也较为显著。对参数间的交互作用进行分析,结果见图5和图6。
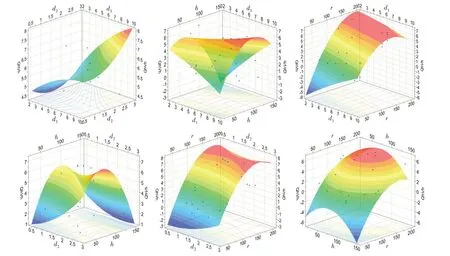
图5 两两参数与QhVh之间关系的响应曲面Fig.5 Response surface between two parameters and QhVh

图6 两两参数与η之间关系的响应曲面Fig.6 Response surface between two parameters and η
当d2固定时,随着d1的增大,QhVh呈增大趋势,且d2的变化对这一趋势影响不大。QhVh随着d1、d2的增大而逐渐增大,从图中可看出d1、d2表现出一定程度的交互作用。
当d1固定时,随着h的增大,QhVh先逐渐增大之后又逐渐减小,且d1的变化对这一总的趋势影响很小。当h较小时,随着d1的增大,QhVh先增大后减小,当h较大时,随着d1的增大,QhVh逐渐增大。参数d1、h表现出较强的交互作用。
当h固定时,随着r的增大,QhVh逐渐增大并最终趋缓。当r固定时,随着h的增大,QhVh先增大然后减小,呈现出抛物线形。参数h和r表现出较强的交互作用。
d1和d2对η的响应呈现出蝶形(见图6)。当d2固定且较小时,随着d1的增大,η先增大后减小,当d2固定且较大时,随着d1的增大,η先减小后增大。当d1固定且较小时,随着d2的增大,η先减小后增大,当d1固定且较大时,随着d1的增大,η先增大后减小。参数h和r表现出较强的交互作用。
从以上分析可以看出,参数间的交互作用对底部冲刷动量和作业效率有着不同程度的影响,有必要在响应面模型中考虑交互项。
根据以上四个参数的一次项、交互项与二次项拟合出响应面模型,如下式所示:

式中,xi为自变量,x1~x4分别表示d1、d2、h、r,β0为常数项,βi为一次项的系数,βij(i≠j)为交互项的系数,βij(i=j)为二次项的系数。方程各项系数见表3。
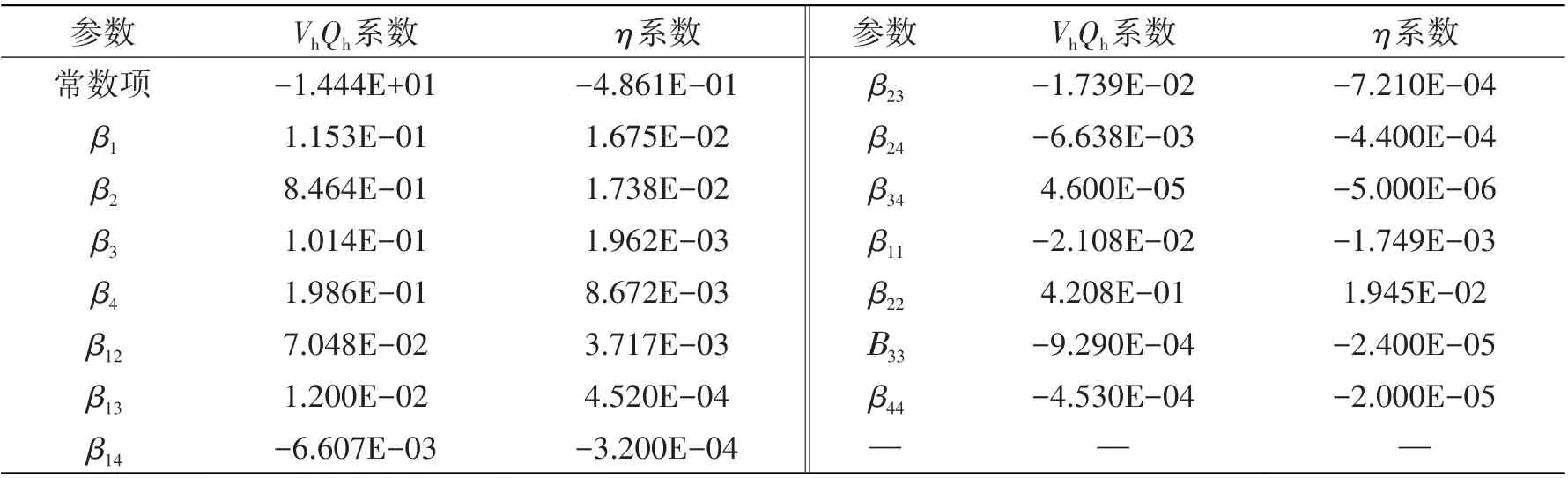
表3 底部冲刷动量QhVh、作业效率η响应面模型表达式各项系数Tab.3 Response surface model expression coefficients of QhVh and η
2.4 模型方差分析与检验
图7和图8分别给出了底部冲刷动量QhVh和作业效率η的响应面模型散点图,图上的散点整体接近图上的直线,说明拟合值(模型解)接近实际值(分析解),即模型的拟合效果好。
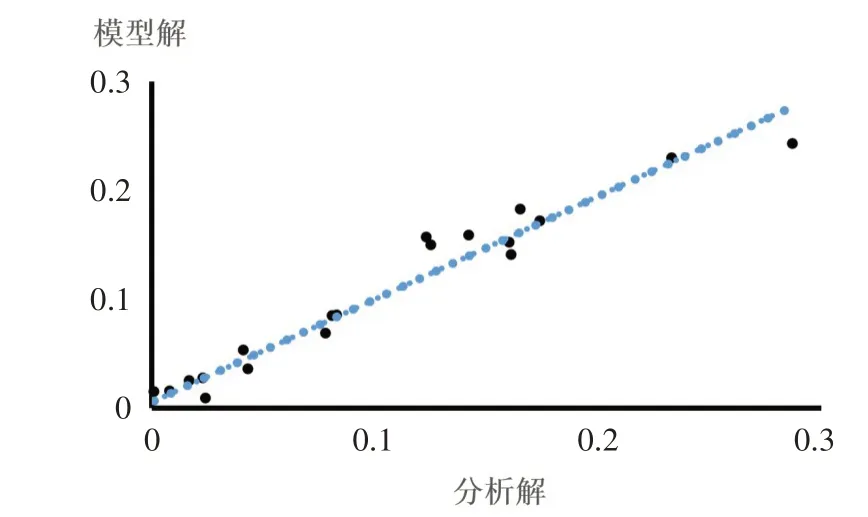
图7 底部冲刷动量QhVh响应面模型散点图Fig.7 Scatter diagram of response surface model of QhVh
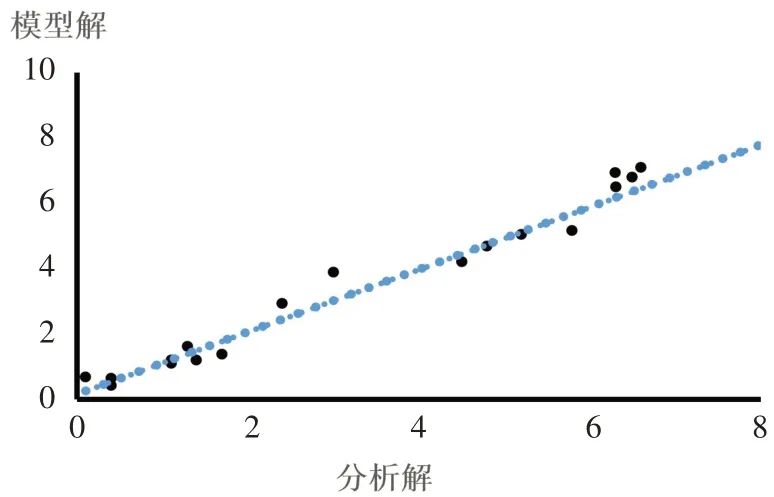
图8 作业效率η响应面模型散点图Fig.8 Scatter diagram of response surface model of η
底部冲刷动量响应面模型复相关系数R2=0.954、校正复相关系数R2adj=0.824;作业效率响应面模型复相关系数R2=0.946,校正复相关系数R2adj=0.806,表明在经过考虑因子数的校正后,通过该模型可以解释原数据在均值附近的变化中82.4%的成份(冲刷动量模型)和80.6%的成份(作业效率模型),模型拟合效果良好。底部冲刷动量和作业效率响应面模型的变异系数(coefficient of variation)分别为3.305和3.692,说明试验具有足够的精确度与可信度。
2.5 优化方案及其结果分析
建立目标函数和设计变量之间关系式后,采用多目标粒子群优化算法(MOPSO)对其进行求解,优化算法所采用的相关参数为:每代粒子数20,迭代步数30,惯性权重取值0.9,两个学习因子均为1.0。优化结果见图9,图中“□”为最优解集,即两目标函数优化结果——Pareto前沿。最优解集及其对应的设计变量见表4。选择Optimal 1、Optmal 3 和Optmal 6 三个代表性的方案进行数值验证,进口压力为12 个大气压时,主要参数(流速和流量)的计算结果见表4。
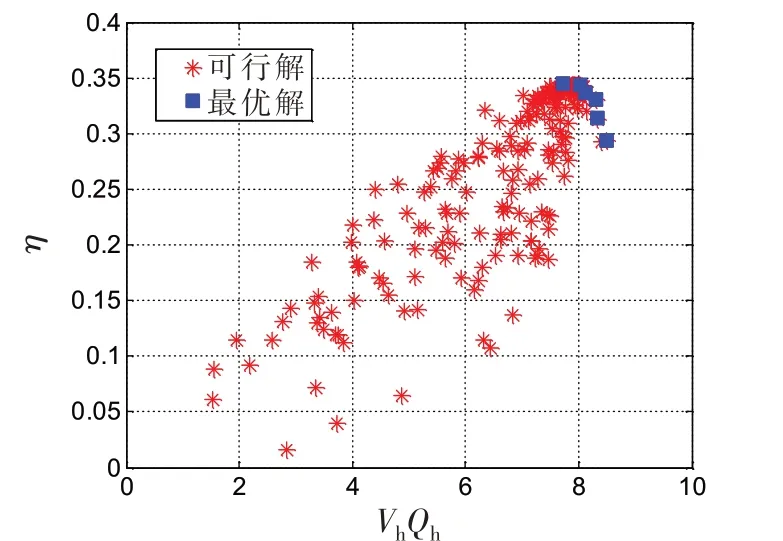
图9 两个目标函数的可行解与最优解Fig.9 Feasible solution and optimal solution of two objective functions
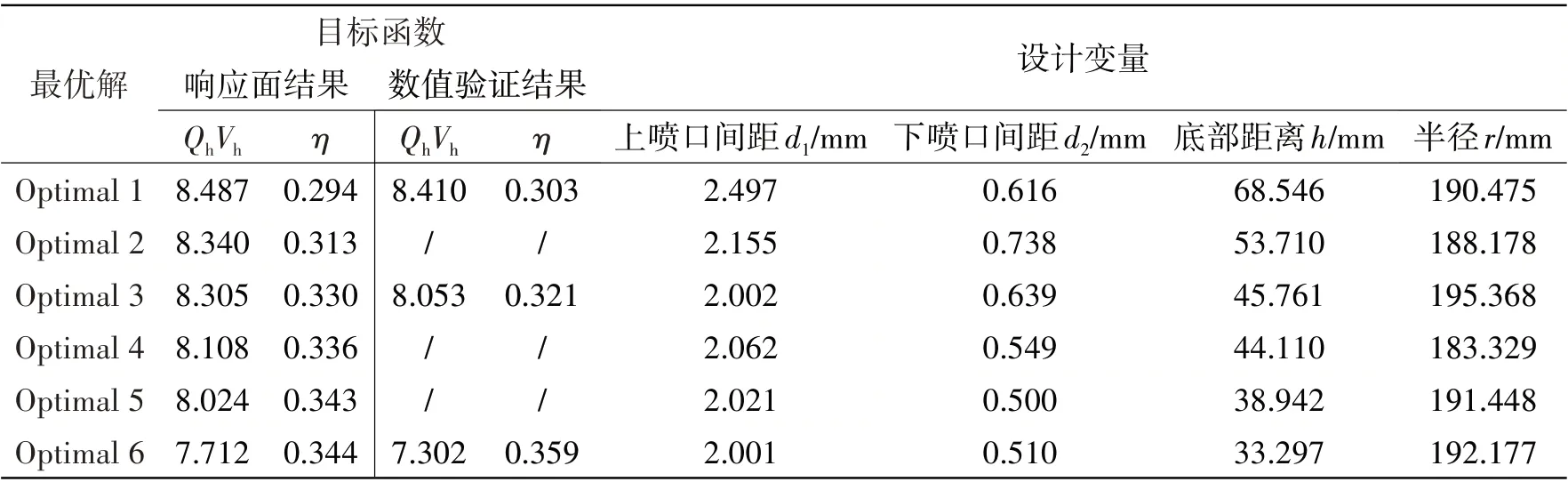
表4 优化方案的目标函数及设计参数Tab.4 Objective function and design parameters of optimization cases
从图9可以看出:最优解集逐渐收敛,呈现凸形,最优解集对应的设计变量除底部距离外,差异不太大;上喷口间距d1范围在2.0~2.5 mm之间,下喷口间距d2范围在0.5~0.6 mm之间,半径r范围在180~190 mm之间,底部距离h范围在30~70 mm之间。
从表4 可以看出:响应面模型优化获得的最优解经数值验证后,底部冲刷动量QhVh和有效作业效率η误差在5%左右,三个方案的大小趋势一致。说明所建立的响应面模型能够表征两个设计目标与设计变量的关系。
图10~12 分别给出了P=12 atm 时三个优化方案的速度云图和流线图。从中可以看出:Optimal 1的底部速度明显大于Optimal 3 和Optimal 6,这与底部冲刷动量也大于其他两个方案是一致的;Optimal 1的底部对称面附近出现了较大的涡,Optimal 3和Optimal 6很小,从作业效率来看Optimal 6最大。
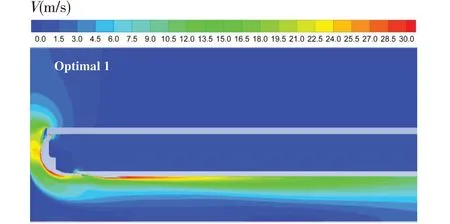
图10 Optimal 1的速度云图(P=12 atm)Fig.10 Speed contours of Optimal 1 at 12 atm
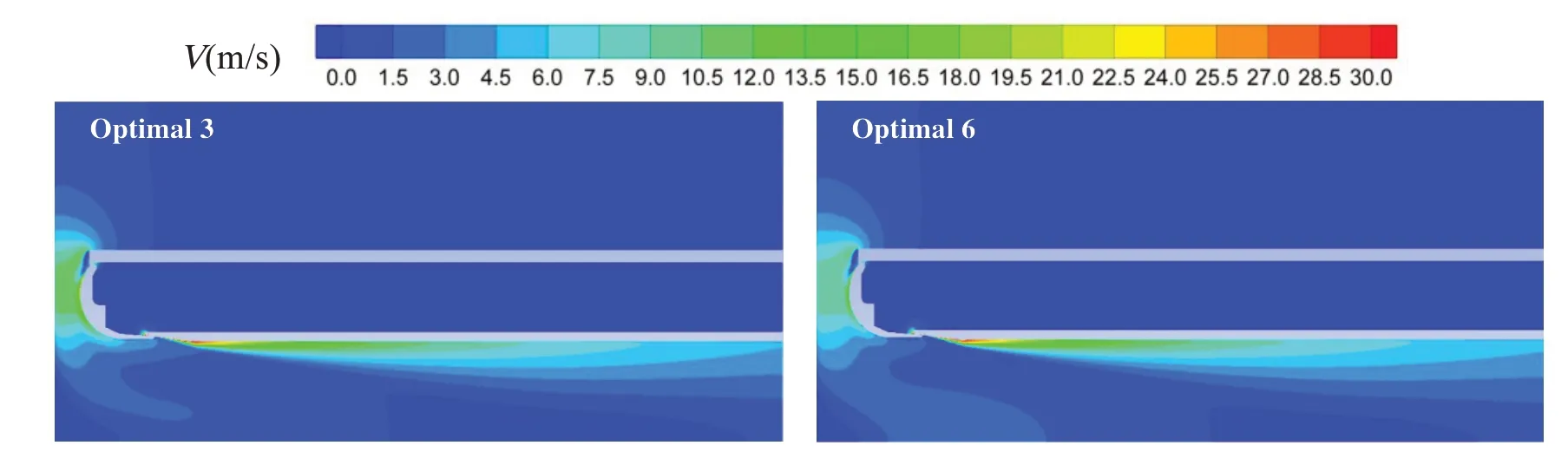
图11 Optimal 3和Optimal 6的速度云图(P=12 atm)Fig.11 Speed contours of Optimal 3 and Optimal 6 at 12 atm
从响应面模型的优化结果及其数值验证可知:所建立的响应面模型能够较好地反映目标函数与设计变量之间的关系;两个目标函数较佳方案所对应的设计变量上喷口间距d1、下喷口间距d2、半径r基本上收敛于某个较小范围内,底部距离h范围较大。
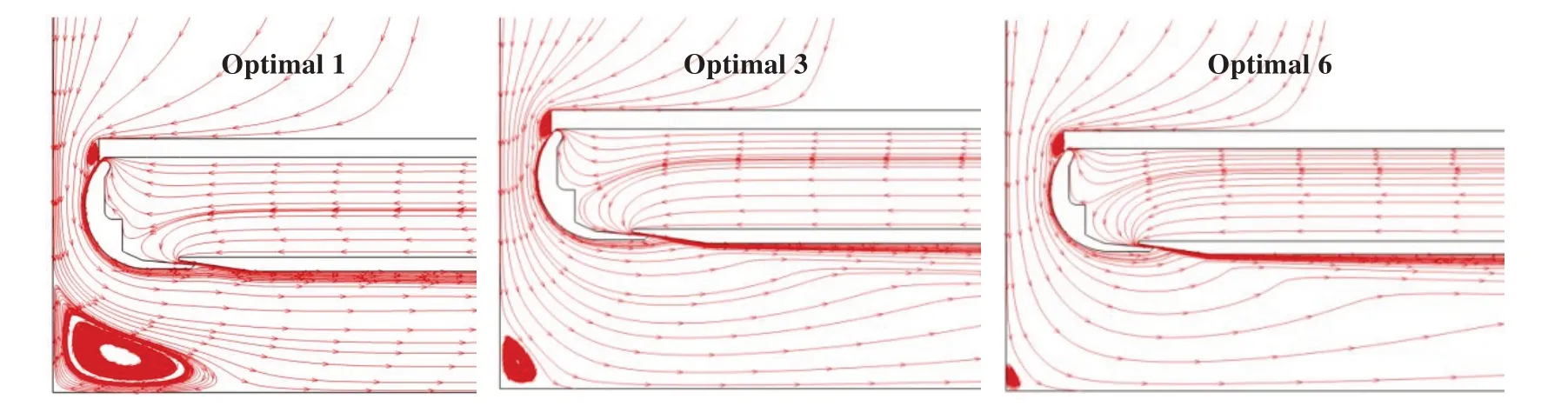
图12 三个优化方案的流线图(P=12 atm)Fig.12 The flow lines of Optimal 1、Optimal 3 and Optimal 6 at 12 atm
3 结 论
本文以基于RANS 的数值计算方法作为清淤泵性能的评估手段,利用试验设计方法详细分析了泵的设计参数对性能的敏感性;在此基础上,建立设计参数与性能的响应面模型,通过粒子群优化算法对其求解获得了最优方案,并对最优方案的性能进行了数值验证。得到的主要结论如下:
(1)利用试验设计方法能够有效地分析设计参数对响应的敏感性以及参数之间的交互作用。各设计参数中,影响底部冲刷动量和作业效率的敏感参数为底部距离h和出口半径r,另外四个参数间的耦合效应也较为显著。利用这些参数建立响应面模型,可较为精确地逼近参数与性能之间的函数关系。
(2)基于RSM 的清淤泵设计参数优化设计获得的最优方案集中,Optimal 3 的底部冲刷动量为8.053 m4/s2,作业效率为32.1%,明显高于试验设计中20个方案的结果,充分说明了基于RSM的清淤泵设计方法可获得设定目标最佳所对应的清淤泵设计参数。
