跟网型逆变器的非线性模型及稳定性分析方法

程 成，谢少军，谭玲娟，周潇庆，许津铭，钱 强

（1. 南京航空航天大学自动化学院,江苏省 南京市 211106；2. 河海大学能源与电气学院,江苏省 南京市 211106）

0 引言

并网逆变器作为分布式能源与电网的功率接口,其性能好坏直接影响到输入电网的电能质量［1-3］。在跟网型逆变器控制中,通常采用锁相环来实现受控的并网电流与电网相位同步［4］。在强电网条件下,锁相环输入为独立的电网电压,锁相环及并网逆变器之间为串联结构,因此,可将两者单独进行系统稳定性分析。然而,随着可再生能源发电的快速发展,以及考虑到配电网中较长线路、变压器漏感等的影响,电网往往呈现出弱电网特性［5-6］。在弱电网情况下,锁相环输入通常为公共耦合点（point of common coupling,PCC）电压或滤波器电容电压［7-9］,由此造成了并网逆变器、锁相环及电网之间的相互耦合,进而易引起低频谐振及谐波稳定性问题［10］。此外,由于锁相环中的坐标变换以及基准生成环节存在着关于系统状态的三角函数运算,锁相环具有较强的非线性特性,这使得弱电网下的跟网型逆变器研究更为复杂。因此,如何准确模拟和分析弱电网下带有非线性环节的并网逆变器是跟网型并网逆变器研究的重要课题［11-12］,也是并网逆变器系统分析及设计的关键之一。

小信号模型被广泛用于分析锁相环的非线性问题,非线性锁相环在静态工作点处被线性化为易于处理的线性模型,并在此基础上建立逆变器的输出阻抗模型以支持阻抗稳定性分析。文献［13-15］以1/4 周期延迟的锁相环为研究对象,采用了基于小信号模型的阻抗稳定性分析方法,结果表明,锁相环对两倍锁相环带宽内的逆变器系统的稳定性具有较大影响。为此,文献［16-17］通过在锁相环输入端引入二阶低通滤波器或复数滤波器以改善系统在弱电网下的鲁棒性能。然而,文献［11］指出上述锁相环建模过于简单地将α轴和β轴分量处理为一对完全正交的信号,并仅考虑锁相环输入输出频率一一映射。为建立更为准确的系统模型,文献［18-19］在计及谐波耦合效应的前提下,提出了基于谐波传递矩阵的并网逆变器多频传递函数模型,并采用广义奈氏曲线分析系统阻抗稳定性,结果显示该方法在预测系统稳定性的准确性方面得到了较大的提高。然而,谐波传递矩阵方法同样只适用于静态工作点处的小范围扰动情况,当系统受到较大的暂态扰动时［20］,系统状态将偏离静态工作点,由此产生较大的线性化误差使得所建模型精确度降低。

在跟网型逆变器的同步稳定性问题中,文献［21-24］将受控的逆变器等效为一个电流源,并通过非线性理论对弱电网下锁相环的暂态同步稳定进行分析。然而,弱电网下的锁相环、逆变器及弱电网三者相互耦合,将逆变器通过等效为电流源分析的解耦并没有得到定量的分析,因此,基于解耦前提的非线性建模及分析方法存在严谨性问题,需要进一步研究更严谨的考虑逆变器系统全局稳定的非线性分析。

鉴于以上讨论,本文将采用非线性理论方法研究弱电网背景下的跟网型逆变器系统。首先,建立了并网逆变器的整体非线性状态空间模型,其中非线性部分的有界条件通过计算获得。为得出全局稳定条件,通过建立二次Lyapunov 函数,并引入松弛因子,将非线性的有界条件代入系统全局稳定条件的推导中。借助MATLAB 软件对系统参数进行逐点分析,以明晰在非线性判据下系统参数对稳定性的影响。最后,通过一系列暂态实验证实了本文所提非线性建模及分析方法的正确性及有效性。

1 跟网型逆变器的非线性建模

弱电网下的LCL 型单相并网逆变器系统如图1所示。图中：SPWM 表示正弦脉宽调制；L1、L2为滤波器电感；C为滤波电容；Lg为电网阻抗,考虑到电网阻抗的阻性部分有利于系统稳定,电网阻抗在这里考虑为纯感性以表示最恶劣的情况；vdc为直流源电压；vin为逆变器输出电压；ic为电容电流；ig为被控的并网电流；vp为PCC 电压；vg为理想的电网电压；电流控制器中采用了常见的电容电流反馈来实现对LCL 滤波器谐振的阻尼,并使用比例-积分（PI）电流调节器及PCC 电压单位前馈策略来减少基波跟踪误差并实现较好的动态性能。与PCC 电压同步的电流参考幅值iref通过锁相环模块产生；kad为有源阻尼反馈系数；e-τs表示数字计算延迟,其中τ为延迟时间。为简化计算,图1 中控制信号至逆变器输出的等效增益kpwm被设置为1［25］。

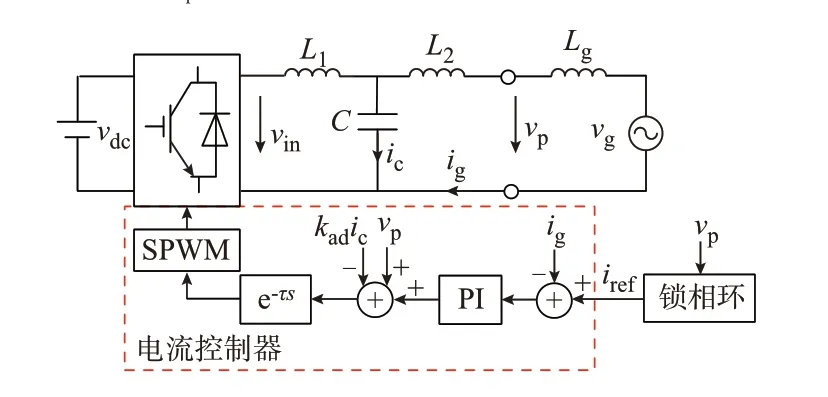
图1 单相并网逆变器结构Fig.1 Structure of single-phase grid-connected inverter

将图1 简化为图2,能够直观地观察出锁相环、受控的逆变器以及电网之间相互耦合。

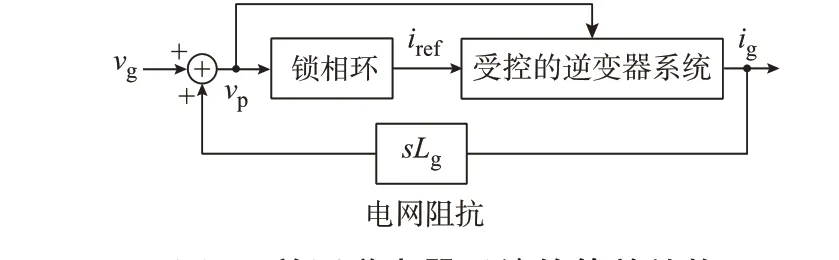
图2 并网逆变器系统的等效结构Fig.2 Equivalent structure of grid-connected inverter system

1.1 锁相环的非线性模型

考虑到二阶广义积分器对输入具有一定的滤波功能,可以适应小范围的电网频率变化,应用于并网逆变器时性能优良。如图3 所示,本文针对基于二阶广义积分器的锁相环进行建模。图中,PCC 电压经过二阶广义积分器产生一对正交信号uα和uβ,通过非线性的Park 变换产生相位误差信号ud,PI 调节器将ud调节至0 以实现对PCC 电压的相位跟踪,后经过积分环节获得相角θ,电流参考则进一步通过对相角的正弦运算获得,其中i*为电流参考幅值,kpl和kil为锁相环中的PI 参数。需要指出的是,应用于逆变器的锁相环的输出侧通常采用cos(·)运算,本文为了能够得出非线性函数的有界不等式,在锁相环中采用sin(·)运算,并将PI 调节器的输入改为ud以实现同步。

图3 基于二阶广义积分器的锁相环结构Fig.3 Phase-locked loop structure based on secondorder generalized integrator

锁相环输入端的二阶广义积分器的Laplace 域表达式为：

为便于后续的系统稳定性分析,定义锁相环环节的状态向量为：

1.2 逆变器系统模型

根据图1 中的LCL 型滤波逆变器电路结构,可得如下连续状态空间模型：

根据基尔霍夫定律可得：

矩阵A中的N=[0,1-l,0,0,0]。

2 全局稳定性判据

2.1 非线性项的处理

为推导稳定性判据,需要找到非线性f（θ）与系统状态x之间的不等式关系。

首先,对于Park 变换中的非线性函数g（θ）,可得如下不等式：

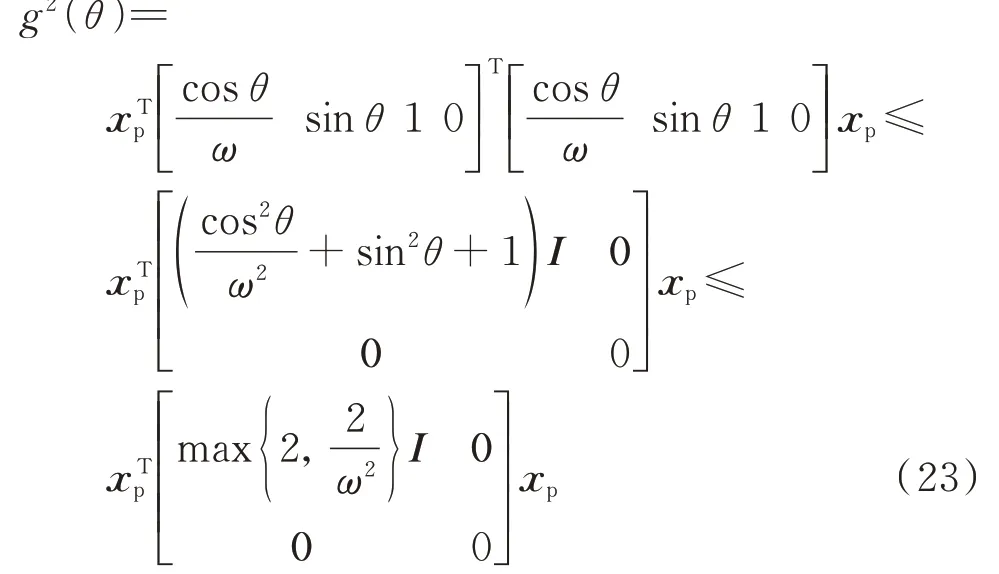
式中：I为适维的单位矩阵。

电流参考生成环节中的非线性函数ρ（θ）则可以重新表达为ρ(θ)=k(θ)θ,其中k(θ)=(θ-sinθ)/θ。图4 展示了k（θ）函数曲线,可以看出k(θ)为关于θ的有界函数,其范围为k(θ)∈[0,1.217 3]。因此,可得如下不等式：

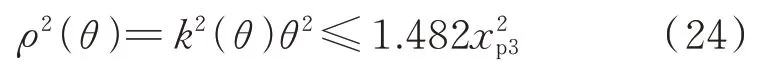
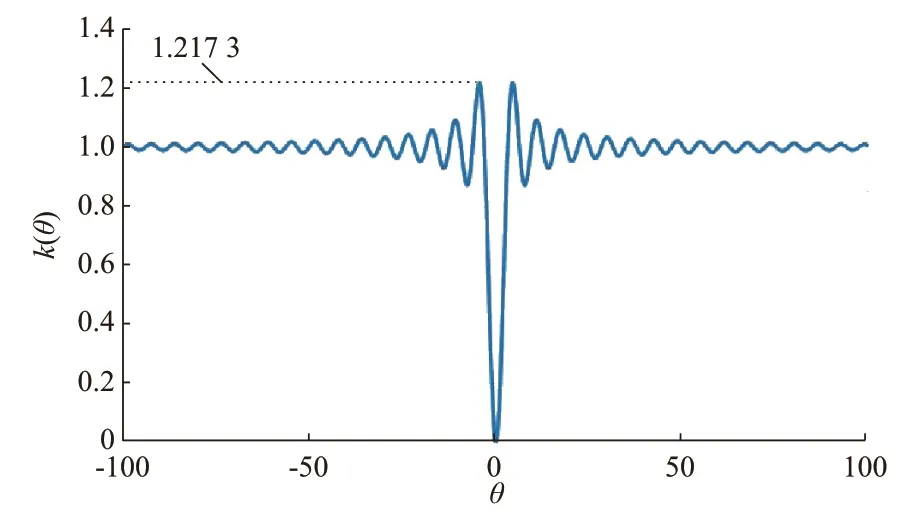
图4 k(θ)函数曲线Fig.4 Curve of function k(θ)

2.2 系统稳定的不等式条件

选择Lyapunov 函数为V[x]=xTPx,其中P为正定矩阵。根据Lyapunov 稳定性判据可知,若使得系统渐进稳定,则需dV[x]/dt ＜0。实际上,对于并网逆变器状态空间模型（式（21））,若存在正定矩阵P以及正实数ε1、ε2,使得矩阵不等式（25）成立,则系统（式（21））在有界条件（式（23）、式（24））的约束下满足dV[x]/dt＜0,即整个并网逆变器系统能够渐进稳定（证明过程如附录A 所示）。

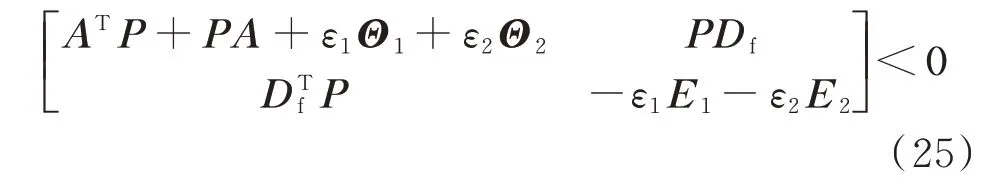
式中：E1=diag{1,0}；E2=diag{0,1}；

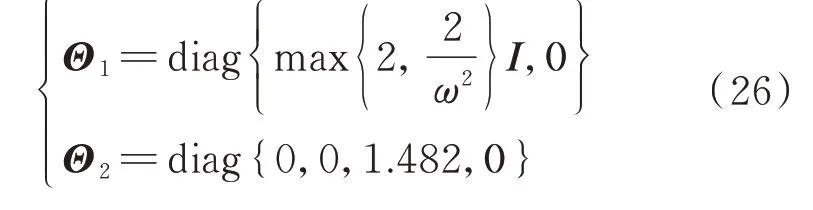
3 稳定域分析

为进一步分析锁相环及电网阻抗对系统稳定域的影响,本章将通过MATLAB 软件对各个参数进行逐点验证,系统分析中的固定参数如附录B 表B1所示。将各个待验证的控制参数（即kp和ki）代入矩阵A、Df时,不等式（25）为一个线性矩阵不等式,通过MATLAB 软件中的LMI 工具箱求解不等式（25）,若可解,则所代入的控制参数满足稳定条件。具体验证过程如图5 所示,其中参数所验证的区间为kp∈[kp,min,kp,max],ki∈[ki,min,ki,max],下标min 和max 分别表示最小值和最大值。

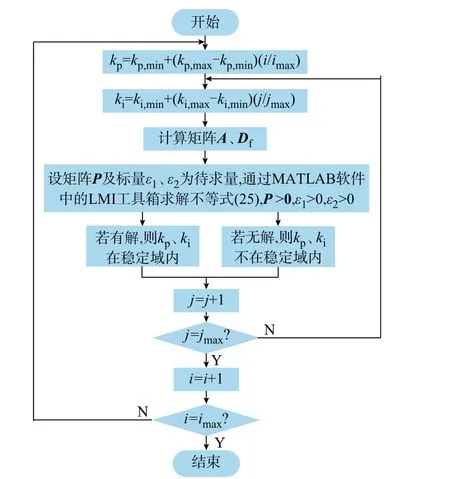
图5 稳定域的验证流程图Fig.5 Flow chart of stability region verification

3.1 电网阻抗对稳定域的影响

通过使用如图5 所示的逐点验证方法,并设kp,min=ki,min=0,kp,max=24,ki,max=40 000,imax=jmax=200。不同电网阻抗下的参数稳定域如附录B图B1 所示,可以看出,随着电网阻抗的增加,系统PI 参数的稳定域缩小。此外需要指出的是,现有基于线性矩阵不等式的稳定性分析中,通常将电网阻抗的不确定区间通过Polytopic 型不确定模型引入稳定条件的推导。但在实际的弱电网情况下,电网阻抗的不确定范围较大,这种区间推导方法将使得分析结果具有极大的保守性,甚至可能导致条件失效而得不到稳定域,在文献［26-28］中,所研究的电网阻抗范围仅为0～1 mH。本节对不确定的电网阻抗进行逐点验证,这使得稳定性分析能够面向更宽范围的电网阻抗变化。

3.2 电流参考幅值对稳定域的影响

附录B 图B2 给出了强/弱电网背景下,iref分别为1 p.u.和0.5 p.u.时的稳定域范围。从图B2（a）中可以看出,在强电网下,电流参考幅值的设置对系统稳定性没有影响,这是由于锁相环输入为独立的电网电压,这使得锁相环与逆变器为相互独立的子系统。从图B2（b）中可以看出,电流参考幅值的增大减小了系统的稳定域,这是由于iref的增大等效增加了整个系统的环路增益,使得稳定裕度降低。

4 实验验证

为验证所提出的稳定性分析方法的有效性,搭建了单相T 形中点钳位型并网逆变器系统,逆变器参数如附录B 表B1 所示,逆变器采样及控制均由DSP TMS320F28335 实现。电网阻抗则通过在逆变器输出侧串联的电感模拟。出于安全考虑,以下实验在较低的电压等级下进行,逆变器输出通过可调变压器与市电相连。

4.1 基于非线性模型分析的稳定域验证

实际上,在PI 控制器中,比例参数kp越大,系统响应速度越快且低频的环路增益越高；积分参数ki越大,稳态误差越小但动态性能越差［29］。为权衡系统性能并留有一定的稳定裕度,选取Lg∈[0,6]mH条件下系统稳定域内的PI 参数kp=6,ki=5 000 作为逆变器的控制参数（记为“例1”,如附录B 图B1 所示）。由于传统的锁相环建模采用的是在静态工作点处线性化的小信号模型,在小扰动情况下并没有明显的偏差。因此,本节将在各种暂态事件（包括电流参考幅值突变、电网阻抗突变以及电网电压骤降）下进行实验测试。

当Lg分别为3 mH 和6 mH 且iref在0.5 p.u.与1 p.u.之间突变时的暂态实验波形如附录B 图B3 所示。从图中可以看出,在所分析的电网环境下,系统是暂态稳定的。从稳态时的并网电流性能来看：较大的电网阻抗会导致较大的并网电流总谐波畸变率（THD）值；较大的电流基准时THD 值较小,这是由于电网电压扰动相对变小。

为模拟电网阻抗突变的暂态情况,电网阻抗通过2 个3 mH 的电感串联模拟,并在其中一个电感上并联一个可控开关。开关从闭合切换至断开时电网阻抗从3 mH 突增至6 mH；开关从断开切换至闭合时电网阻抗从6 mH 突降至3 mH。附录B 图B4 给出了在iref=1 p.u.下,电网阻抗突增和突降时的暂态实验波形。从图中可以看出,在电网阻抗突变的暂态事件下系统依旧稳定。

此外,通过调节逆变器与市电相连的变压器,进一步模拟了电网电压骤降的暂态情况。附录B图B5（a）给出了iref=1 p.u.、Lg=6 mH 时电网电压从1 p.u.快速降落至0.5 p.u.的暂态实验波形,从图中可以看出,系统在电网电压快速下降的暂态事件下能够稳定运行。在相同的条件下,通过仿真软件Simulink 测试了电网电压突降时的暂态波形,如图B5（b）所示,从中可以看出,系统依旧能够稳定运行。

从以上3 个暂态事例的实验测试结果可以看出,系统在参数“例1”下能够保持暂态稳定,这与上一节的稳定域分析的结果一致。

4.2 非线性模型与小信号模型的对比

将变流器的PI 控制参数改为kp=6、ki=7 000（即附录B 图B1 中的“例2”）,从图B1 中可以看出,基于本文建立的非线性模型及分析方法,当iref=1 p.u.、Lg=6 mH 时,预测系统是不稳定的。但从附录B 图B6 可以看出,基于锁相环小信号模型而推导的阻抗比的Nyquist 曲线未穿过(-1,0)点,这意味着根据线性化模型及传统分析方法预测系统是稳定的。附录B 图B7给出了在参数“例2”下,iref从0.5 p.u.突增至1 p.u.的暂态实验波形。从图中可以清晰地看出,当iref突增时系统立即失稳,并在半个周期之后触发保护。此外,图B7 还给出了当iref=1 p.u.时,参数“例2”下的稳态实验波形,波形显示系统在此情况下是稳定的。因此,图B7 的暂态不稳定现象是由于暂态扰动造成的,这充分说明了传统的小信号分析并不能准确地预测系统的暂态稳定。这是因为小信号模型是在稳态工作点处线性化推导而来的,当系统受到暂态扰动时,模型存在较大的误差,继而导致分析结果不准确。这也证明,相比于传统的小信号模型和稳定性分析方法,本文提出的非线性稳定性分析方法更为准确,且适用于暂态稳定性分析。

5 结语

针对弱电网背景下的跟网型逆变器,计及锁相环非线性特性对系统稳定性的影响,建立了一种非线性状态空间模型,并基于非线性系统理论提出了满足全局稳定的不等式判据及稳定性分析方法。

基于本文提出的跟网逆变器非线性模型和稳定性分析方法,可以得出逆变器在不同电网阻抗、进网电流下的稳定域。与基于小信号模型的研究结论一致,基于非线性模型的稳定性分析同样表明了电网阻抗以及电流参考幅值的增大不利于系统稳定。同时,暂态实验表明,由于线性化误差的存在,传统的小信号模型并不能准确地预测系统的暂态稳定性,而本文提出的非线性模型和分析方法可以准确地预测系统的稳定性。

此外,需要指出的是,由于锁相环结构的特殊性,非线性状态空间模型及矩阵不等式稳定条件的推导较为复杂,系统不稳定机制不够直观。因此,无法像阻抗分析法那样能够作为系统设计的重要依据。虽然提出的方法能够给出绝对严格的稳定域,但结果也具有一定的保守性。因此,降低稳定条件的保守性以及力求提供直观的非线性分析方法将是需要进一步开展的工作。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。