基于分散协同多阶段鲁棒调度的电热联合系统灵活性增强方法
2022-03-23施云辉郭创新
施云辉,郭创新
(浙江大学电气工程学院,浙江省 杭州市 310027)
0 引言
加速清洁能源转型是中国能源发展的战略目标[1],然而含有随机性和波动性特征的新能源大规模、高比例并网将给电网的安全运行和清洁能源消纳带来巨大挑战。制约新能源消纳的主要因素之一是供能系统的灵活性不足,其中较为突出的是以“三北”地区为代表的电热联合系统(integrated electrical and heating system,IEHS)。在冬季夜晚,通常电负荷较低,而热负荷往往较高,热电联产(CHP)机组需保持一定出力以满足供热需求,导致新能源出力的空间被压缩。与此同时,由于处于电负荷低谷,火电机组往往缺乏向下爬坡容量,这使得风电的向上爬坡事件难以被充分响应,进一步导致弃风。
为了提升IEHS 的灵活性,学界对IEHS 中能量的生产、传输、消费等多方面展开了研究。在供能侧,文献[2]分析了加装电锅炉(EB)、储热等设备在提升热电厂灵活性方面的作用。文献[3]在热网配置了调峰EB 的基础上,进一步建立了考虑储热式电锅炉的优化调度模型,分析了配置方式对弃风率的影响。文献[4]详细比较了热泵、EB、储热等设备提升CHP 运行灵活性的作用。在网络侧,文献[5-7]考虑了热网的传输时延特性,建立了IEHS 优化调度模型,证明了热网的惯性在提升风电消纳方面可以发挥类似于热储能的作用。在用能侧,文献[6-7]建立了考虑建筑物热传输特性和用户舒适度的优化调度方法,可以在不降低用能感受的前提下提升风电的消纳。文献[8-10]研究了热能的需求侧响应和主动负荷对风电消纳等经济性指标提升的作用。文献[11-12]研究了考虑电动汽车的协同优化调度模型,并给出了实际案例分析。文献[13]则进一步综合考虑了源侧灵活性改造和荷侧可调节负荷对风电消纳的协同提升作用。
现有文献对提升IEHS 灵活性的各种物理手段做了充分挖掘,但在算法层面较少考虑风电出力存在的随机性,大多仍沿用传统的确定性调度模型,这限制了对灵活性资源的利用程度。文献[14]考虑了建筑物热惯性,提出了基于机会约束规划的调度模型,相比于确定性调度可以更充分利用热负荷的调节能力,但该方法依赖于风电预测误差的精确分布。文献[15]基于两阶段鲁棒优化,建立了IEHS机组出力计划及备用计划联合优化模型,降低了传统调度方法的保守性,但未能考虑到储能充放电的非线性特性。文献[16]提出基于多阶段鲁棒优化的IEHS 实时调度方法,相比于传统滚动时间窗方法,其计算速度更快、风险出现概率更小,但其研究的设备较为单一。其次,现有方法大多为集中式优化方法,需要由单一的分析决策中心收集各子系统的详细模型和边界条件,在电力系统和热力系统分属于不同运营商的情况下,不利于保护两者的隐私。
针对以上问题,本文聚焦于IEHS 的实时调度,提出了基于分散协同多阶段鲁棒优化调度的IEHS灵活性增强方法。首先,建立了考虑EB、电储能(ES)、建筑物热惯性等多种灵活性资源的IEHS 模型,针对其中储能的非线性特性,提出了基于“预估-矫正”的储能状态转移方程,保证了模型的凸性。接着,利用盒式不确定集对风电预测误差不确定性进行建模,并提出了基于多阶段鲁棒优化的IEHS 实时调度模型。进一步,为了保护不同运营商的隐私,将所提模型分解为时空耦合的2 组动态规划问题,并设计了分散协同鲁棒对偶动态规划(decentralized robust dual dynamic programming,D-RDDP)算法进行求解,求解过程仅需较少的信息交换。为了衡量所提模型提升IEHS 灵活性的效果,提出了基于线性优化灵敏度分析的灵活性指标,包括爬坡速率敏感度、发电容量灵敏度、储能功率灵敏度和储能容量灵敏度。最后,通过算例分析了所提模型及算法的有效性。
1 IEHS 建模
本文研究的IEHS 的结构如图1 所示。其中,电力子系统包含火电机组、风电场、ES 及电负荷,热力子系统包含CHP 机组、EB、热负荷,2 个子系统分属不同运营商。负荷所需电能由火电机组、CHP 机组、风电场产生,经由电力线路供应,所需热能通过CHP 机组和EB 产生,经由热力管网供应。IEHS 中的热力管网控制模式分为恒温恒流、恒温变流、恒流变温、变温变流4 种[17]。本文中考虑恒温变流的控制模式,该模式的调节速度快、供热舒适度较好,在一些发达国家如丹麦已经得到广泛应用[17]。
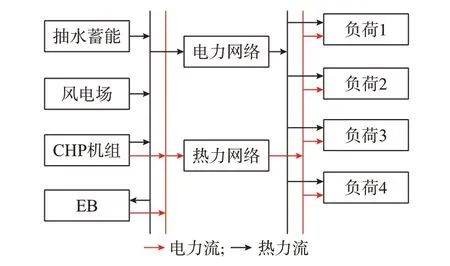
图1 IEHS 基本结构Fig.1 Basic structure of IEHS
1.1 热力子系统模型
CHP 机组是热力子系统的核心,其能量转换关系如下:

式中:Hg,t为CHP 机组g在t时段的产热功率;Pg,t为CHP 机组g在t时段的产电功率;kCHPg为CHP 机组g的热电比;SCHP为CHP 机组集合。
除此之外,CHP 机组的其他出力特性可以等效为火电机组建模,CHP 机组和火电机组运行所需的燃料成本可以由产电功率的分段线性函数表示,即

在IEHS 中,EB 相当于用电机组g,其出力特性由式(6)表示。

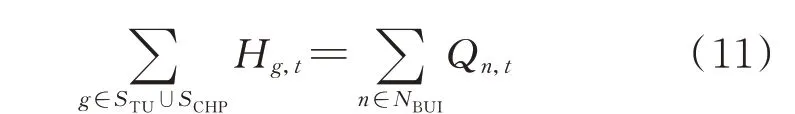
1.2 电力子系统模型


2 IEHS 分散协同多阶段鲁棒调度模型
2.1 多阶段鲁棒调度模型

IEHS 的分散协同调度在本文中采用主从模式,即电力子系统观测到风电实际出力后,根据电力平衡制定t时段产电计划,并将Pψ,t发送给热力子系统,接着热力子系统根据热力平衡制定t时段供热计划。电力子系统和热力子系统制定供能计划的模型分别见式(30)—式(32)和式(33),其中t既表示时段索引,又表示阶段索引,即求解t阶段的优化问题给出t时段的最优决策。模型式(31)—式(34)均为动态规划模型,这是因为各子系统每个时段的决策都需考虑到对未来时段的影响,下面分别进行说明。


2.2 储能的预估-校正状态转移方程
如上文所述,求解动态规划问题式(31)—式(34)的关键在于电力子系统WCTVF、SVF 和热力子系统VF 的逐次逼近。然而,由于ES 充放电指示变量的存在,电力子系统每一时段的优化问题均为混合整数线性优化问题,这会使电力子系统WCTVF 成为非凸的函数,其逼近将极为复杂。解决该问题有2 种思路。第1 种思路是将约束式(20)—式(22)中的充放电指示变量去除,仅保留充放电功率变量,这可以使原问题转化为线性规划问题。然而,文献[20]证明了该方法仅适用于对于各时段间没有耦合的模型,或是不考虑弃风代价的模型。第2 种思路是利用整数包络的方法,将所有的状态变量都用0-1 变量表示,例如,可将储能SOC 变量Se,t在其取值范围内N等分,用阶梯形式的SOC代替连续的SOC,并相应地引入N+1 个0-1 变量,如式(35)所示。由于任何自变量为0-1 变量的函数都可以被一凸函数包络,因此可以利用整数割来逼近VF[21]。但该方法的代价是引入的0-1 变量数目极其庞大,仅适用于小规模系统。

式中:Ke,t,q为第q分段的储能SOC。
本文采取与上述方法均不同的储能预估-校正状态转移方程,来凸化电力子系统每一时段的优化问题。由于储能的充放电效率一般较高,抽水蓄能的整体效率可达到80%,锂电储能的效率可达到95%,充放电所带来的能量损失相比于其带来的减少弃风和失负荷而言微不足道,在单时段优化的过程中暂时忽略储能的充放电效率对最优解的影响不大。因此,可用单一的充放电功率PESSe,t来代替原模型中的充电和放电变量,并将约束式(18)和式(19)改写为:
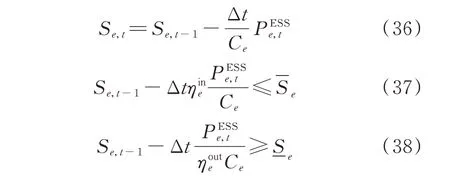
约束式(36)即为储能下一时段SOC 的预估式,约束式(37)和式(38)是为了保证不管储能处于充电状态还是放电状态,下一时段的SOC 均不会越限,因此式(37)和式(38)保证了约束的安全性。由于预估式(36)对下一时段的SOC 计算并不准确,因此在求解后一时段问题时,还需要根据以下方程更新SOC:

2.3 D-RDDP 算法


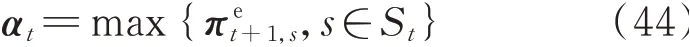
动态规划问题式(31)—式(34)具有分散协同的结构,算法求解电力子系统t阶段问题时不需要获知热力子系统的模型及出力计划,求解热力子系统t阶段问题时也仅需要获知电力子系统期望的热力子系统供电功率,不需要获取内部模型,两者仅通过VF 耦合。基于这样的特征,设计D-RDDP 算法,如附录A 图A1 所示,通过逐次迭代的方法训练模型式(31)—式(34)。
在D-RDDP 算法中,每次迭代包含正向遍历和反向遍历2 个部分,其中正向遍历(t=1,2,…,T)电力子系统接收上一阶段电力子系统状态变量,计算当前阶段最坏情况风电出力和电力子系统状态变量,传递电力子系统状态变量给下一阶段的电力子系统,并传递耦合变量给热力子系统,热力子系统接收本阶段耦合变量以及上一阶段热力子系统状态变量,计算当前时段热力子系统状态变量,并传递给下一阶段的热力子系统。反向遍历(t=T-1,T-2,…,1)电力子系统根据上一阶段电力子系统状态变量对应的对偶变量,添加约束至上一阶段电力子系统,热力子系统根据上一阶段热力子系统状态变量对应的对偶变量和本阶段耦合变量对应的对偶变量,分别添加约束至上一阶段热力子系统和本阶段电力子系统。当电力子系统的最坏情况VF 上界和下界足够接近时,算法收敛。
通过D-RDDP 算法在日前阶段对模型进行训练,在日内运行时可根据实时的输入信息对决策进行优化,该流程如图2 所示。
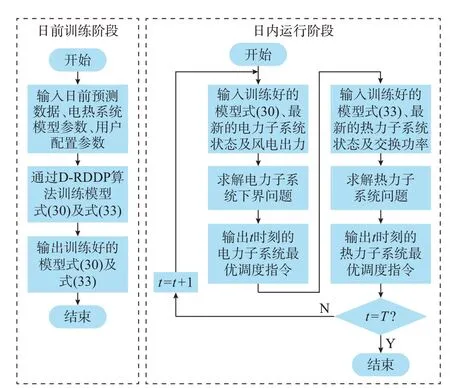
图2 IEHS 分散协同多阶段鲁棒调度流程图Fig.2 Flow chart of decentralized and coordinated multi-stage robust dispatching of IEHS
2.4 IEHS 调度策略灵活性评价指标
供能系统的灵活性可以定义为利用其资源来响应净负荷波动的能力[23],传统意义上针对供能系统的灵活性评价指标包括调峰能力、爬坡能力、负荷响应能力等[24]。由于本文的侧重点在于利用先进的调度模型增强已有供能系统的灵活性,因此提出以下针对调度模型的灵活性评价指标。
2.4.1 爬坡速率敏感度
单台机组的爬坡速率敏感度是指增加一单位该机组爬坡/滑坡速率使系统总运行成本产生的减少量。对于整个系统而言,爬坡速率敏感度ΠR可以定义为:

2.4.2 发电容量敏感度
单台机组的发电容量敏感度是指增加一单位的机组最大发电功率或减小一单位机组最小发电功率使系统总运行成本产生的减少量,在IEHS 中,由于锅炉相当于用电机组,因此也纳入考虑。对于整个系统而言,发电容量敏感度ΠC可以定义为:

2.4.4 储能容量敏感度
单个储能的容量敏感度是指增加一单位的最大SOC,或减小一单位的最小SOC 使系统总运行成本产生的减少量。由于建筑物也起到储热的作用,因此一并纳入考虑。对于整个系统而言,储能容量敏感度ΠSE可以定义为:

以上4 种基于敏感度的评价指标,每一项均对应了模型式(1)—式(27)中某一个约束,如爬坡率敏感度对应爬坡约束式(4)—式(5),而线性优化目标函数关于约束右端项的敏感度可以通过对偶理论求解。当调度计划不触及系统的调节瓶颈时,所对应的敏感度系数就为0,因此以上4 种敏感度指标越小,说明算法越能充裕应对风电的波动,等价地使得系统的灵活性变得更强。
从附录A 图A2 可以更清楚地说明这一点,图中π1和π2分别表示该场景该时段下目标函数关于机组1 和2 的爬坡速率的敏感度,计划1 和计划2 中2 台机组的总出力相同,但计划1 将机组1 安排在最大出力点,机组2 安排在最小出力点,当下一时段风电大幅增发时(假设增发量大于单台机组爬坡能力,小于2 台机组爬坡能力),仅有机组1 可以向下爬坡,而机组2 已经无法继续减少出力。然而,仅靠1台机组的向下爬坡无法抵消风电的增发,因此产生弃风。假设机组1 的爬坡速率更大一些,那么弃风量就会减少,系统总成本降低,因此π1>0,而机组2的瓶颈在于最小出力,增加机组2 的爬坡速率无济于事,因此π2=0。反观计划2,由于机组1 和2 均安排在适中的出力点,当下一时段风电大幅增发时,2台机组都可以向下爬坡,增加任何一台机组的爬坡速率对成本都没有影响,因此有π1=π2=0。
3 算例分析
3.1 算例设置
采用6-母线5-节点的IEHS 作为测试算例,见附录A 图A3。其中,电力子系统包含6 个节点、2 台火电机组(G1 和G2)、1 座风电场W 及1 个ES,ES 的SOC 初态为0.45,终态的容许值在0.3~0.6 之间。热力子系统通过节点F连接于电力子系统,供热设备包含1 台CHP 机组以及1 台EB,热负荷包含4 个采暖负荷(HD1 至HD4)。CHP 机组的热电比为1.5,室内温度控制在20~26 ℃。电负荷预测、风电预测及室外温度预测如图3 所示。图中,以15 min为1 个时段,下同,以红色阴影部分为风电预测的95%置信区间,风电日发电量(均值)/日负荷量为0.6,极端时段下风电功率(预测上界)/负荷功率达到87%。设备及建筑物的详细参数见附录A 表A1至表A4。算例分析中算法均通过Julia 语言的JuMP.jl[25]优化建模工具包实现,计算机配置为Xeon E5-2678 CPU,64 GB RAM。

图3 电负荷、风电及室外温度预测Fig.3 Forecasting of electrical load, wind power and outdoor temperature
算例中将比较以下3 种模型,通过风电出力的蒙特卡洛采样分析其平均性能和最差性能,收敛因子ε设为0.01,不确定因子α设为0.3。
1)经典滚动调度模型。在每个时段采集当前的系统状态和风电实际出力,求解未来1 h 的IEHS 优化调度问题,执行下一时段的调度指令,更新系统状态,以此类推。该方法无需训练。
2)集中式的IHES 多阶段鲁棒调度模型(用CMSRD 表示)[16]。在该方法中,电力子系统和热力子系统的优化问题将被统一求解,并用单一的最坏情况VF 来表征风电极端场景下未来的运行成本。采用集中式的RDDP 算法[16]在日前阶段训练该模型。
3)本文所提分布式的IHES 多阶段鲁棒调度模型(用D-MSRD 表示)。采用分布式的D-RDDP 算法在日前阶段训练该模型。
3.2 算法收敛性验证
在迭代80 次后,D-MSRD 收敛,观察图4 所示的各VF 迭代情况可以发现,热力子系统TVF 收敛较快,6 次后即收敛到阈值。电力子系统SVF 和预想的一致,紧密跟踪热力子系统TVF,在迭代7 次后收敛。电力子系统TVF 上界及下界由于不确定因子α的设定较大,收敛相对较慢,以避免早熟,在迭代46 次后上下界相对误差小于0.05,在迭代80 次后收敛到0.01。
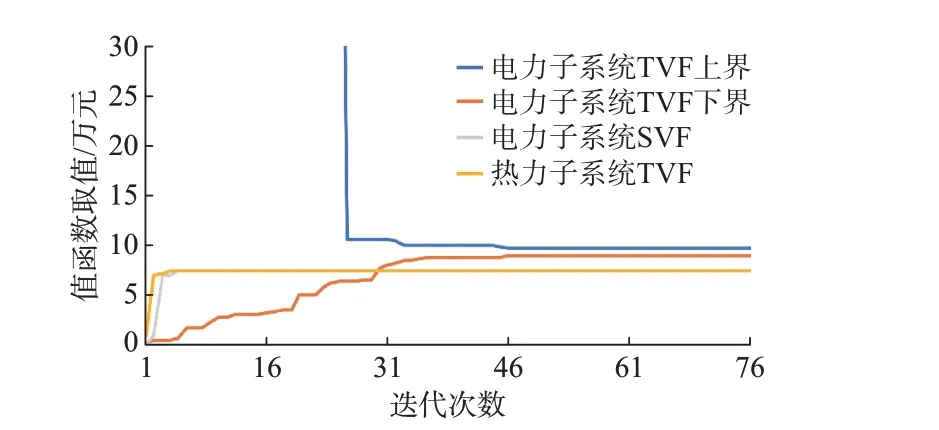
图4 D-MSRD 各VF 迭代情况Fig.4 Iteration situation of each VF for D-MSRD
3.3 模型有效性验证
比较不同模型在1 000 个随机风电出力场景下的指标情况,用以衡量模型在实际数据集下的表现,结果如表1 所示,未达标的指标在表格中用红色标注。经典滚动调度的总成本在平均情况下及最差情况下均要劣于C-MSRD 及D-MSRD,其主要原因是其负荷补偿成本较大,最差情况下达到了14.94 万元。与之形成对比的是在风电消纳率方面,经典滚动调度超额完成了设定的95% 风电消纳率,而C-MSRD 和D-MSRD 在最坏情况下的风电消纳率为94.7%和94.5%,稍低于设定值,对应的未达标惩罚为0.328 万元和0.546 万元,远小于经典滚动调度额外付出的负荷补偿,因此经典滚动调度并未找到总成本意义上的最优解。进一步观察ES 的SOC 终态,C-MSRD 和D-MSRD 均符合要求,但经典滚动调度则与初态有较大偏离,因此其当日风电消纳率的提高实际上牺牲了下一日的消纳能力,是一种贪心解法。最后,对比D-MSRD 和C-MSRD,由于DMSRD 的分布式算法特性,其指标均会稍劣于集中式算法,用一部分的经济性换取运营商隐私的保护。
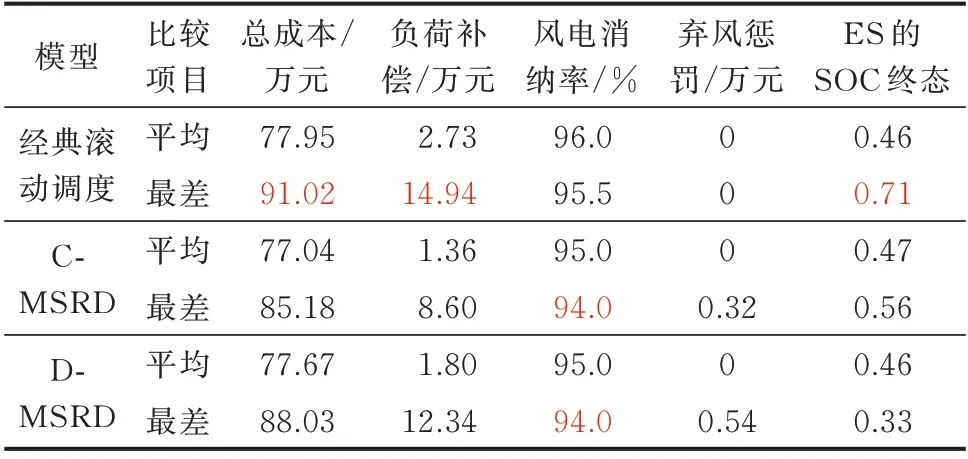
表1 不同调度模型计算结果比较Table 1 Comparison of calculation results for different dispatching models
D-MSRD 得出的最坏风电出力场景下各供能设备的出力见附录B 图B1(a),对图B1(a)进行分析可以发现,风电出力的最坏场景为在净负荷低谷时段大发,在净负荷高峰时段少发,而在净负荷或室外温度的爬坡阶段剧烈波动。各供能设备均参与了风电功率波动的平抑,其中以ES 为最,在各时段均频繁充放电。在电力子系统方面,G1 及CHP 机组承担了电负荷基荷,而G2 则起到调峰的作用。在热力子系统方面,通过CHP 机组及EB 的出力调节,改变供热功率来影响热力子系统对电力子系统的电功率交换,从而参与电力子系统的风电波动平抑,例如05:00—08:00 时段,风电大发,室内温度维持在最低值,这使得CHP 机组可以尽可能地降低出力,从而最大限度地发挥供暖负荷的灵活性,与此同时各时段建筑物的室内温度都维持在设定区间内,见图B1(b)。
3 种模型的灵活性指标测算结果如表2 所示,得分越低说明灵活性越强。在爬坡速率敏感度和发电容量敏感度方面,C-MSRD 的指标得分最低,DMSRD 次之,经典滚动调度最高,但差距不明显,这是因为对于常规机组和CHP 机组的控制而言,只需考虑相邻时段的耦合,滚动调度与C-MSRD 和DMSRD 并不存在明显差别。而在储能功率敏感度和储能容量敏感度方面,同样是C-MSRD 的指标得分最低,D-MSRD 次之,经典滚动调度最高,但差距则较为明显,这是由于储能的控制需要考虑全时段的耦合,也是MSRD 方法的优势所在。
3.4 算法可靠性验证
D-MSRD 模型采用的D-RDDP 算法,依赖于电力子系统和热力子系统之间的可靠通信。为了模拟实际通信环境下对算法收敛性的影响,假设传输的数据有0%~15%的概率出现丢包,即算法1 中固定连接变量和更新电力子系统SVF 的步骤有相应概率失败,验证不同丢包率下算法的收敛性,迭代次数均设为100 次,结果如表2 所示。不同丢包率下,经100 次迭代均能收敛至较低值,对偶间隙随着丢包率的增加而增加。平均总成本和最坏情况下总成本也随着丢包率的上升而上升,在丢包率大于9%时,最坏情况下总成本已劣于表1 所示的集中式经典滚动调度。因此,为了保证算法所求得的调度计划最优性,控制较低水平的丢包率是有必要的。

表2 不同丢包率下D-RDDP 收敛性比较Table 2 Comparison of D-RDDP convergence with different package loss rates
3.5 算法计算性能验证
为了验证D-MSRD 在中等规模系统中的计算效率,将电力子系统设为IEEE-300 节点算例,8 号机设为CHP 机组。热力子系统包含20 个建筑物,建筑物参数从附录A 中随机选取。迭代200 次后对偶间隙收敛到2.1%,用时778 s。室内温度的控制情况如图5 所示,20 个建筑物室内温度变化趋势类似,且均控制在容许值之内。
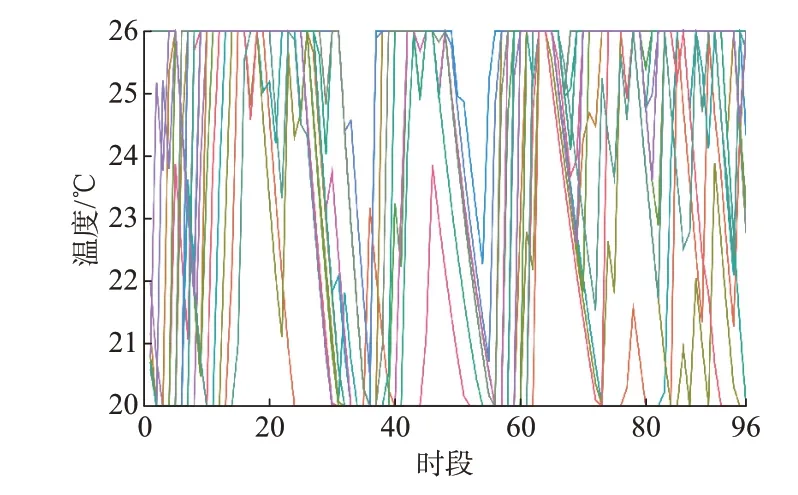
图5 中等规模IEHS 室内温度变化情况Fig.5 Indoor temperature change of medium-scale IEHS
4 结语
本文针对IEHS 中风电出力不确定性,并考虑不同能源运营商的隐私保护,提出了分散协同的多阶段鲁棒调度模型,相比传统调度方法,可充分发挥储能、电热转换设备、建筑物热惯性这些灵活性资源应对风电出力波动的作用。通过WCTVF 和SVF的耦合,各子系统每一阶段的决策都能计及对其余时段、其余子系统的影响,克服了传统滚动调度短视的缺陷。算例结果表明,平均总成本和最坏情况下总成本都能达到更优解,可确保储能的SOC 返回初态,并且室内温度也可控制在容许范围内。所提模型相较于传统的滚动调度模型,在储能运行灵活性方面和机组运行灵活性方面均有所提升,但提升储能运行灵活性的效果更为显著。所提D-RDDP 算法可以使分布式模型的训练对于中等规模系统亦能在较短时间内收敛,相比于集中式算法所需的信息交换更少,并且在通信收到干扰时亦能正常工作。
下一步的研究可考虑更多不确定性因素,如热力子系统中的室外温度不确定性等。此外,本文中电热子系统的耦合基于交换功率指令,研究基于价格信号耦合的IEHS 多阶段鲁棒调度亦是有价值的研究方向。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。
