直流电压准无差修正的VSC-MTDC 系统协同优化下垂控制

2022-03-23刘昊宇刘崇茹王群乔

电力系统自动化 2022年6期

刘昊宇，刘崇茹，郑乐，王群乔

（新能源电力系统国家重点实验室（华北电力大学）,北京市 102206）

0 引言

中国资源和负荷中心的分布呈现东西跨度大、南北距离远的特点［1］,基于电压源型换流器（voltage source converter,VSC）［2-3］的柔性直流输电系统输电容量大［4］、输送距离远［5］、不需要电网辅助换相［6］,充分契合中国能源传输需求。而多端柔性直流输电（voltage source converter based multi-terminal high voltage direct current,VSC-MTDC）系统［7-9］运行方式灵活多变,在清洁能源消纳和深远海风电送出领域具备突出优势［10-12］。下垂控制［13-15］采用多站协同的方式消纳直流网络中的不平衡功率,可同时利用多个VSC 的功率调节能力,在VSC-MTDC 系统中应用较广。但下垂控制存在一个明显弊端,即换流站通过调节直流电压使直流网络潮流重新分布,实现不平衡功率的吸收,但直流电压偏移会威胁系统安全经济运行。

针对下垂控制伴生的直流电压偏差问题,学者研究形成了3 类主要改进方法。第1 类方法使用Washout 滤波器［16-18］代替下垂系数,将比例形式的误差输入变为比例-积分（PI）形式以消除控制静差。文献［16-18］依次在微网、新能源并网等领域应用基于Washout 滤波器的有功功率-直流电压下垂控制,实现直流电压稳定控制。第2 类方法在下垂控制参考值上叠加直流电压误差的PI 输出［19-20］,利用PI 的稳态无静差特性实现直流电压无差调节。文献［19-20］分别将直流电压偏差的PI 输出叠加至直流电压和有功功率参考值上,实现了直流电压的无静差控制。这2 类方法本质都是将一个下垂控制站转为直流电压控制站,实现的无静差控制仅针对主站直流电压。同时,系统中的不平衡能量将由控制主站完全承接,丧失下垂控制多站协同的优秀特性。第3 类方法是主动调整下垂控制的有功功率参考值［21-24］,通过平移下垂曲线的方法实现直流电压无差调节。文献［21-22］采集本站有功功率偏差,叠加至下垂控制有功功率参考值上,通过移动下垂曲线使换流站运行于额定直流电压。文献［23-24］采用的是一种分级下垂+功率参考值修正的集中控制模式,全系统的不平衡功率增量叠加至主功率平衡站下垂控制参考值上,实现直流电压稳定控制。第3 类方法解决了前2 类方法丧失下垂控制多站协同能力的问题,但实现的直流电压无差调节仍属于“伪无差”调节,各VSC 直流电压和有功功率与调整前的稳态数据均存在偏差,而且对于不平衡功率动态变化的情况缺乏有效手段。

针对直流电压调节方法存在的问题,本文基于第3 类方法提出一种直流电压动态修正的VSCMTDC 系统改进下垂控制。主要工作包括以下3 个方面：

1）直流电压完全无差调节的不可行性分析：利用数学推导证明了采用下垂控制的VSC-MTDC 系统遭受功率扰动时,各站保持扰动后功率不变的同时将直流电压恢复至初始状态的假设无法成立。

2）兼顾功率扰动和直流电压调节的优化下垂控制：提出一种协同优化下垂控制,以下垂站功率扰动最小和直流电压调节效果最优为目标,优化下垂控制功率参考值,以极小的VSC 功率波动为代价将直流电压恢复至最接近初始值的状态,实现直流电压的“准无差”调节。

3）附加直流电压控制器（additional DC voltage controller,ADCVC）：设计ADCVC,以直流电压变化量为输入,模拟同步发电机惯性和阻尼,在功率扰动过程中自动调节有功功率参考值,改善直流电压。

1 下垂控制电压偏差分析

1.1 系统模型与控制原理

图1 为VSC-MTDC 系统示意图,其中VSCi表示第i个柔性直流换流站,ACk表示第k个交流系统。直流电网由VSC 间的直流架空线连成,不存在直流节点［25］。

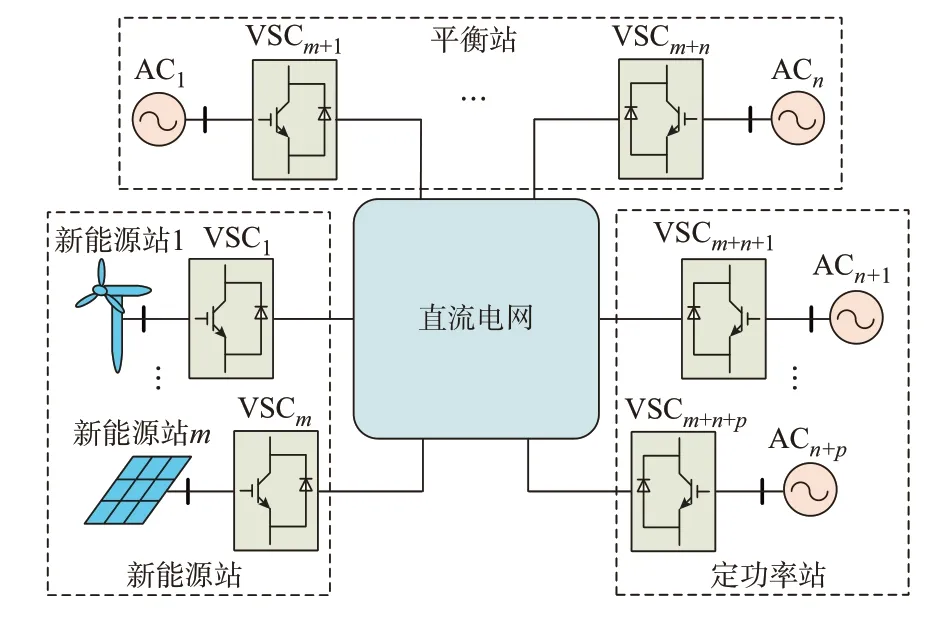
图1 VSC-MTDC 系统示意图Fig.1 Schematic diagram of VSC-MTDC system

m个新能源站受风电、光伏出力影响,通常采用定交流电压幅值-频率控制［26］,在消纳波动的有功功率的同时,为新能源站提供稳定的交流电压支撑。n个定功率站通常采用定有功功率控制［27］,以满足交流系统对稳定、优质的有功功率输入的要求。p个平衡站采用下垂控制［13］消纳不平衡功率,以发挥VSC-MTDC 系统中多个交流系统的功率协同调节能力,系统的直流电压由平衡站决定。下垂控制的结构与运行特性如附录A 图A1 所示。

由附录A 图A1（a）可得：

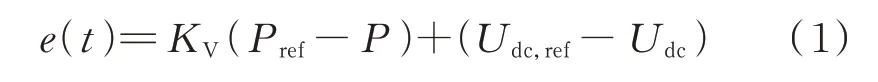
式中：e（t）为PI 输入；Pref和P分别为VSC 有功功率参考值和实际值；Udc,ref和Udc分别为VSC 直流电压参考值和实际值；KV为下垂系数。

考虑PI 稳态输入控制为零［14］,式（1）化为：

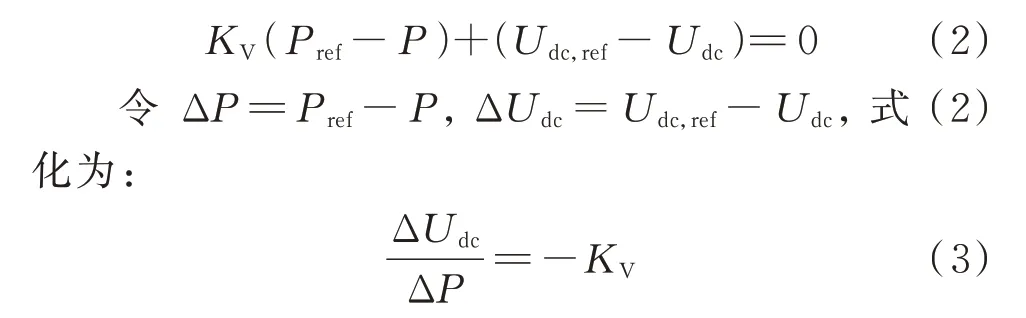
根据式（2）和式（3）可绘制附录A 图A1（b）的下垂特性曲线。当系统发生功率扰动时,VSC 将沿着斜率为-KV的下垂曲线移动到运行点（P1,Udc,1）或（P2,Udc,2）,从而消纳不平衡功率［15］。VSC 在提供功率增量ΔP的同时,必然伴随着直流电压偏差ΔUdc。

1.2 直流电压偏差计算

规定有功功率流出VSC 为正,流入为负。设初始稳态时m个新能源站的总有功功率PWP为：

式中：i=m+1,m+2,…,m+n。

假定动态过程直流损耗Ploss恒定,则各VSC 直流电压同步变化［25］,即各VSC 平均直流电压变化量

式（13）揭示了ΔUdc1同功率扰动量ΔPWP成正比,同n个平衡站下垂系数倒数之和成反比。这说明,VSC-MTDC 系统功率波动后,所有平衡站会协同作用,自动沿着下垂曲线移动,合作完成不平衡功率消纳,伴生的ΔUdc1为第2 章的改进下垂控制提供了研究方向。

2 直流电压动态修正的优化下垂控制

2.1 直流电压无差修正可行性分析

平衡站运行点示意图如图2 所示。初始稳态时,下垂控制的理想运行点为参考点1,但由于直流网损,VSC 实际运行于运行点1。

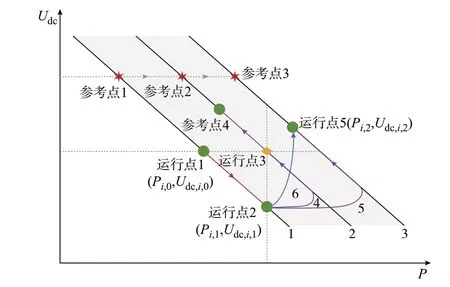
图2 下垂控制运行点变化Fig.2 Changes of operation point of droop control

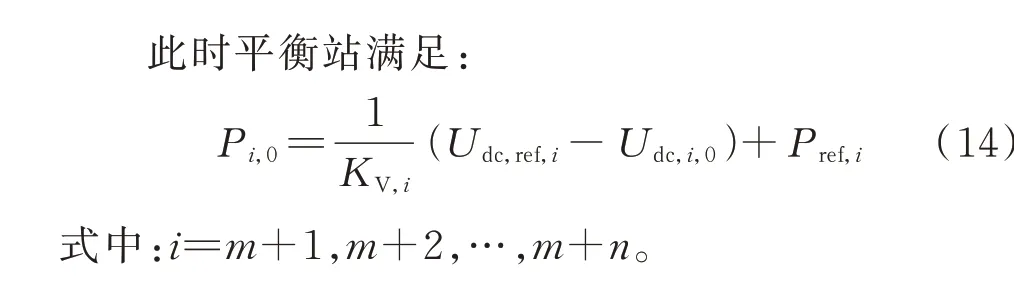
VSCi的有功功率还可表示为：

要实现无功率变动的直流电压无差修正,意味着VSC 将由运行点2 运动至运行点3,并稳定运行。由图2 可知,需将下垂曲线1 沿着P轴平移ΔPi,1,文献［21］即采用该思路。但该想法是不切实的,详细分析如下。

假定系统可以稳定运行于运行点3,新能源站和定功率站出力保持不变。

平衡站下垂曲线1 由于沿P轴向右平移,式（14）写为：

式（22）与式（8）、式（9）和式（16）相吻合。从图2 可知,新能源站出力波动后,为承担不平衡功率,平衡站由运行点1 运动至运行点2,即Pi,0≠Pi,1。式（23）与式（15）等号右侧相同,但左侧分别等于Pi,0和Pi,1,违背实数唯一性原则,系统能稳定运行于运行点3 的假设不成立。

将下垂曲线1 平移ΔPi,1,受PI 性能限制,VSC无法直接由运行点2 阶跃至运行点3,而是会沿曲线4 收敛于下垂曲线2,并沿下垂曲线2 越过非稳定运行点3,到达稳定运行点4。因此,无功率变动的直流电压的无差修正无法实现。

2.2 协同优化下垂控制策略

2.2.1 优化下垂控制

当按照ΔPi,1平移下垂曲线1 来修正直流电压时,VSC 稳定于运行点4,与理想运行点3 存在偏离。于是,本文提出一种具备直流电压动态修正能力的多平衡站协同优化下垂控制策略。通过优化多个下垂站的功率参考值增量,使各VSC 的运行点与运行点3 的欧氏距离最小,协调实现功率扰动最小和直流电压修正最优的目标。

用平方和表征欧氏距离的协调优化函数F为：

式中：IVN,i为VSCi交流电流额定值。

式（24）—式（30）为含约束非线性规划,由附录B 可知F为严格凸函数,在约束范围内最小值唯一。本文采用免疫克隆选择算法［30］寻优。该算法采用抗原和抗体分别表征优化函数和目标解,通过抗体-抗原亲和力筛选种群,使用欧氏距离反映抗体内部亲和力来调整被克隆的抗体,引入多项式变异改善种群多样性并加快收敛。优化求解流程见附录A图A2。

当VSC-MTDC 系统稳定后,载入各VSC 的Pi,1、Udc,i,0及下垂系数KV,j,以式（24）为目标、式（25）—式（30）为约束,采用免疫克隆选择算法进行协同优化。

2.2.2 状态平滑切换方法

将ΔPref,j叠加至平衡站,相当于将下垂曲线1 平移至下垂曲线3。附加功率参考值增量的瞬间,PI输入发生阶跃,受限于PI 响应速度,VSC 无法完全跟踪阶跃的功率参考值,会从运行点2 沿着曲线5波动收敛于下垂曲线3,再沿下垂曲线3 运动至运行点5,完成直流电压修正。该过程VSC 会发生功率冲击,威胁设备运行安全。为削弱冲击,本文提出一种线性状态平滑切换方法,具体公式如下：

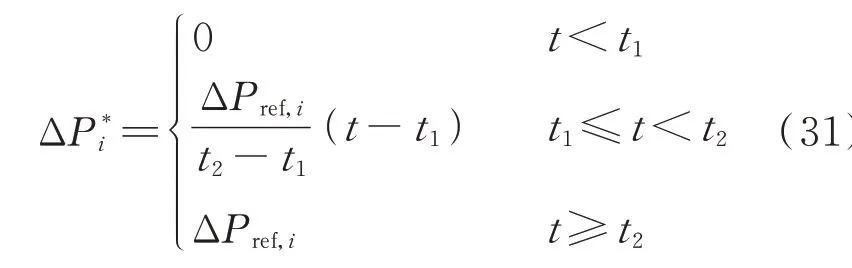
式中：ΔP*i为直流电压调节过程中下垂站有功功率参考值增量的实际值；t1和t2分别为直流电压调节的起止时间。

优化下垂控制在VSC 稳定后进行直流电压调节,因此系统稳定与否是启动线性状态平滑切换方法的先决条件。本文根据VSC 直流电压的导数dUdc/dt是否为零来判断系统是否稳定。对应于实际系统,则采用数值差分法计算dUdc/dt是否为零,具体公式如下：

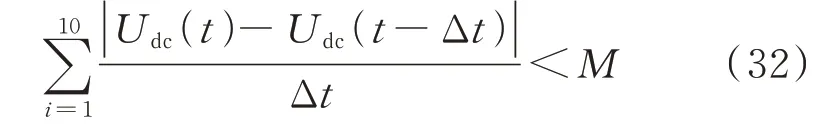
式中：Δt为采样步长；M为一个极小的正数,本文取0.05。

当10 个采样步长的dUdc/dt的绝对值之和小于M时,判定系统稳定,系统控制层取各平衡站反馈的稳态时间最大值作为线性状态平滑切换过程的起始时间t1。

若直流电压恢复太快,VSC-MTDC 系统能量再分配时间不足,容易引发功率冲击,所以状态切换过程的时间间隔不宜太短。考虑到VSC-MTDC 直流电压恢复依赖于VSC 所连交流系统,而发电机的功率调节时间通常为数秒［31］,因此线性状态平滑切换过程的时间间隔设置为5 s,即t2-t1=5 s。

从t1时刻起,第i个平衡站的有功功率参考值增量ΔP*i从0 开始,以ΔPref,i/(t2-t1)的斜率线性增大至理论值ΔPref,i,使VSC 沿着图2 中的蓝色曲线由运行点2 逐步运动至运行点4,避免有功功率参考值阶跃造成电流冲击。

2.2.3 ADCVC 设计

针对优化下垂控制只能在VSC 稳定后进行直流电压调节的问题,设计了ADCVC 改善动态过程中的直流电压。类比同步发电机惯性和阻尼,建立ADCVC,以ΔUdc为输入,通过在功率扰动过程中调节功率参考值,减少直流电压变化值。ADCVC 的控制结构如图3 所示,其中Kp和Ti分别为PI 控制器的比例和积分时间常数,id,ref为d轴电流参考值。

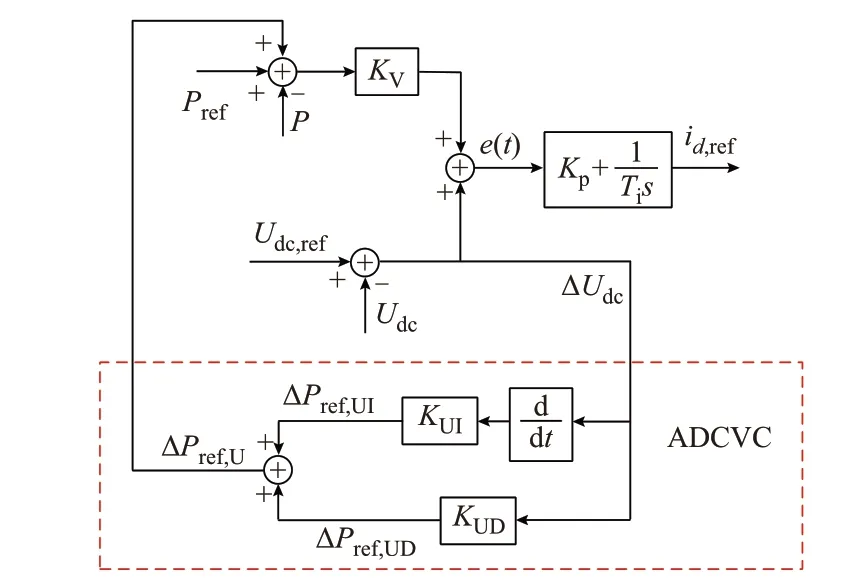
图3 ADCVC 的控制结构Fig.3 Control structure of ADCVC

ADCVC 输出的ΔPref,U由等效惯性增量ΔPref,UI和等效阻尼增量ΔPref,UD组成,具体表达式如下：

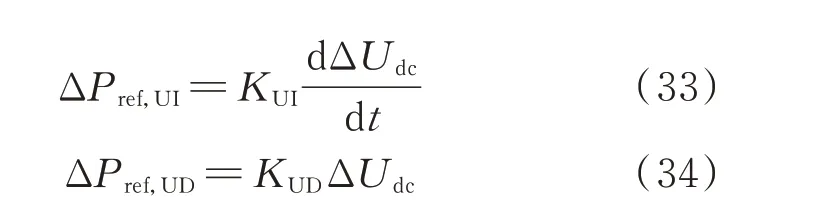
式中：KUI为等效惯性系数；KUD为等效阻尼系数。

功率扰动发生瞬间,dΔUdc/dt通常较大,ΔPref,UI也较大,在扰动初期可提供充分的功率参考值调节量。动态过程结束后,dΔUdc/dt变为零,ΔPref,UI也为零,因此等效惯性控制只在动态过程中发挥作用。而ΔPref,UD在动态过程中逐渐增大,最终会作为新下垂曲线的一部分影响进入新稳态后的直流电压。

2.2.4 控制动作时序

附录A 图A3 为协同优化下垂控制策略的动作时序图。当检测到系统发生功率扰动后（监测功率、直流电压均可）,启动ADCVC；判定系统稳定后,闭锁ADCVC,并将VSC 有功功率参考值更新为当前ΔPref,U和Pref之和；然后启动优化下垂控制计算最优功率参考值,并按照线性状态平滑切换方法进行直流电压调节；若调压过程中未发生新一轮功率扰动,则Udc顺利调节至目标值,否则重启ADCVC。

2.2.5 整体控制策略

图4 为协同优化控制的结构图,Uref,m和fref,m分别为新能源站m定幅值频率控制的交流电压幅值和频率参考值。

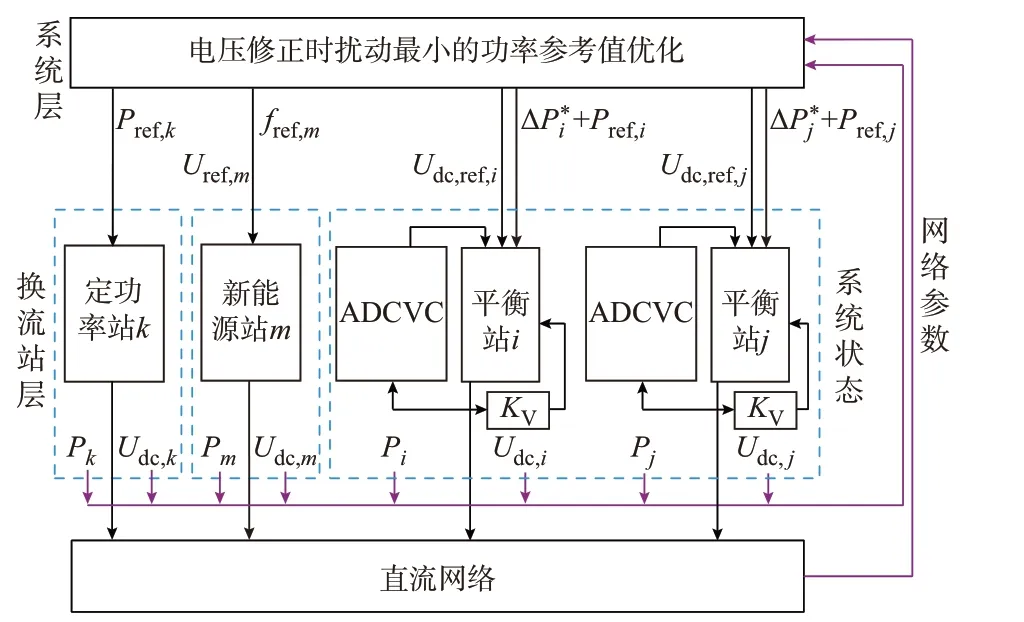
图4 协同优化控制策略Fig.4 Cooperative optimal control strategy

正常情况下,调度中心依据发电计划下发指令值,各VSC 将直流系统状态变量反馈至调度层,实现闭环控制。

新能源场站出力波动后,平衡站下垂控制自动发挥作用,消纳不平衡功率。为改善扰动过程中的直流电压,启动ADCVC,在下垂控制有功功率参考值上叠加ΔPref,UI和ΔPref,UD,动态移动下垂曲线,达到减小直流电压偏差的目的。

扰动后协同优化控制策略发挥作用。调度层根据VSC 实时状态,以式（24）为目标,优化平衡站的ΔPref,j,并以式（31）的线性增长的方式,将ΔP*i下发至下垂站,完成平稳的直流电压修正。

3 仿真验证

3.1 仿真模型

附录A 图A4 为PSCAD/EMTDC 平台上4 端VSC-HVDC 系统仿真模型示意图。VSC1为功率参考值变化的定功率站来模拟出力变化的新能源站,VSC2、VSC3、VSC4为平衡站。系统参数见附录A表A1。

3.2 优化控制策略验证

3.2.1 直流电压偏差计算验证

在t=15 s 时,VSC1的Pref由400 MW 降至300 MW,稳定后的VSC 状态见附录A 表A2。

VSC1至VSC4的直流电压变化量依次为17.16、17.00、17.05、17.00 kV,均值为17.05 kV,各VSC 偏离均值程度小于0.65%。功率突变前后直流网损分别为-3.09 MW 和-2.83 MW,相对误差小于8.41%,表明直流网损不变、VSC 直流电压变化量一致的假定是合理的。此外,ΔUdc1理论值17.07 kV 与仿真均值17.05 kV 的误差小于0.12%,验证了式（13）的准确性。

3.2.2 直流电压调节验证

VSC-MTDC 系统稳定后,在t=30 s 时启动直流电压恢复。表1 为仿真采用的直流电压调节方法。

表1 仿真采用的直流电压调节方法Table 1 DC voltage regulation method adopted in simulation

1）模式1 至4 对比

附录A 图A5、图A6 分别为4 个VSC 的有功功率和直流电压实时状态,表A2 为VSC1功率突变前后各VSC 直流电压和有功功率稳态值,可知原始下垂控制（模式2）在功率突变后,直流电压偏离初始值约17 kV 且一直维持在该值,无自发电压调节能力,进一步遭遇功率波动后易使直流电压越限而引发继电保护动作。

附录A 表A3 和表A4 分别为不同模式下直流电压修正前后各VSC 有功功率和直流电压的稳态值及相对误差,其中模式1 的VSC 以不超过0.04%Pi,1的功率变动为代价,实现了VSC-MTDC系统的直流电压“准无差”调节,Udc,i,2相较于Udc,i,0的误差不超过0.06%。而模式3、4 将VSC2、VSC3和VSC4协同作用的下垂控制变成了以VSC3为主导的定电圧控制,导致被三站分摊的不平衡功率重新被VSC3吸纳。

2）模式1、5、6 对比

令VSC 在0.9～1.1 p.u.内随机生成Udc和ΔPref的初值,使用免疫克隆选择算法求解功率参考值。附录A 图A7 为优化20～214次耗费的平均计算时间。随着优化次数成倍增加,平均时间逐渐稳定于0.017 3 s,验证了本文优化算法的快速性。

模式1、5、6 修正后的功率参考值见附录A 表A5,VSC 响应见图A8 和图A9。由表A6、表A7 可知,无论是模式1、5 还是模式6,VSC 有功功率的理论值和仿真值相对误差均不超过0.06%,直流电压的相对误差均不超过0.03%,证明理论计算的准确性。

将F拆解为表示下垂站整体功率偏移量的FP和表示全系统直流电压逼近量的FU,具体表达式如下：

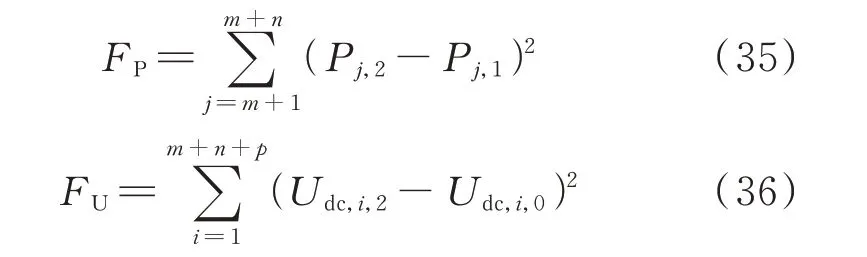
模式1、5 的FP和FU相同,分别为0.01 MW2和0.06 kV2,而模式6 的FP和FU分别为4.31 MW2和1.31 kV2。相较于模式6,模式1、5 的FP和FU分别减小了99.77%和95.42%,即优化协同下垂控制以极小的VSC 功率变动为代价实现了更逼近原始直流电压的扰动后直流电压“准无差”调节。

3）平滑性分析

由附录A 图A8 可知,模式5、6 在直流电压调节启动的瞬间都发生了冲击。对于存在上升沿的时间序列x(t),定义冲击强度指标Γ：

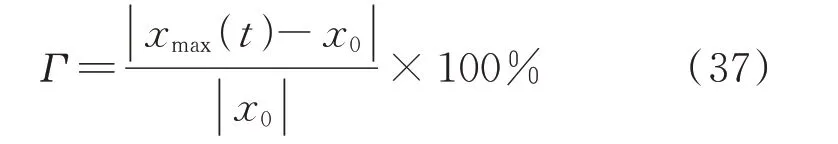
式中：xmax（t）为x（t）动态过程中的最大值；x0为x(t)的初始值。

附录A 表A8 为不同模式电压调节过程的冲击强度,其中模式1 的3 个下垂站的Γ均小于0.86%,而模式5 和6 的分别大于6.86%和6.77%。相较于模式5、6,模式1 的Γ降低超过87.30%,说明平滑措施在直流电压调节时发挥了显著作用。

3.2.3 VSC 重载时直流电压调节验证

将VSC1至VSC4有功功率扩大1.8 倍以验证VSC 重载时的协同优化下垂控制性能。

附录A 图A10 为VSC 重载时的有功功率实时值,表A9 为电压调整前后不同模式的有功功率稳态值及相对误差,可得功率突变后及直流电压恢复后（2 种模式）的Ploss分别为-8.5、-7.93、-7.85 MW,后两者同功率突变后的Ploss相对误差不超过7.65%,说明动态过程中Ploss不变的假定是合理的。相较于Pi,1,模式1 直流电压调节后VSC 有功功率最大偏差为0.2 MW,而模式6 达3.2 MW,前者仅为后者的6.25%,说明模式1 的功率扰动远小于模式6。

附录A 图A11 为VSC 重载时的直流电压实时值,表A10 表示不同阶段各VSC 的直流电压变化量及相对误差,无论是ΔUdc,i,1还是模式1、6 的ΔUdc,i,2（ΔUdc,i,2=Udc,i,2-Udc,i,1）,VSC 的相对误差不超过0.48%,说明VSC 直流电压同步变化的假定是正确的。模式1 的ΔUdc,i,2平均值与ΔUdc,i,1平均值相差0.06%,模式6 的ΔUdc,i,2平均值与ΔUdc,i,1平均值的误差高达8.39%,说明模式1 的直流电压恢复效果明显优于模式6。

结合附录A 图A10、图A11 及表A9、表A10 可知,VSC 重载时采用协同优化控制能以极小的功率偏差为代价,取得远超第3 类方法的直流电压恢复效果。

3.2.4 线路阻抗较大时直流电压调节验证

前述仿真Rij均为1.2 Ω,相较于实际线路偏小。因此,将Rij调至20 Ω 研究线路阻抗较大时协同优化控制的性能。

附录A 图A12 为线路电阻较大时的VSC 有功功率实时值,表A11 为该场景下电压调整前后的有功功率稳态值及相对误差,模式1、6、7 直流电压调节后的Ploss相较于功率突变后的Ploss,误差不超过17.15%,动态过程中Ploss不变的假定仍成立。模式1、6、7 的最大有功功率偏差分别为0.97、26.70、1.34 MW,模式1、7 的最大有功功率偏差仅为模式6的3.63%和5.02%,表明模式6 在进行直流电压调节时,已无法维持有功功率在调节前的水平。

附录A 图A13 为线路电阻较大时的直流电压实时值,表A12 为该场景下各VSC 的直流电压变化量及相对误差,不同状态下VSC 直流电压变化量与均值的误差不超过9.98%。随着线路电阻增大,虽然直流电压变化量分布差异增大,但总体上直流电压变化量仍保持较高一致性。模式6 的ΔUdc,i,2平均值和ΔUdc,i,1的平均值相差40.08%,而模式1 的ΔUdc,i,2平均值和ΔUdc,i,1的平均值误差仅为0.33%,说明线路电阻较大时,模式6 无法将直流电压调节至初始状态附近。

附录A 表A13 为线路电阻较大时不同模式对应的FP和FU,模式1 的FP和FU仅为模式6 的0.26%和2.93%,说明在线路电阻较大时（更贴合实际情况）,无论是有功功率扰动还是直流电压恢复情况,模式1 都明显优于模式6。

本节进一步研究了以标称直流电压为调节目标的协同优化下垂控制（模式7）性能。根据附录A 表A14 中该场景下各VSC 的ΔUdc,i,2,模式1、6、7 的FU分别为364.31、341.70、319.01 kV2。相较于模式1、6,模式7 的FU分别降低12.43%和6.64%,系统直流电压更接近标称直流电压。

本节同时对图2 的正确性进行验证。附录A 图A14（a）至（f）依次为VSC3的功率-电压三维图、有功功率、直流电压、功率-电压运行图、d轴外环PI 输入和实际下垂系数（使用(Pref+ΔP*i-P)KV+(Udc,ref-Udc)=0 计算）。VSC3最初稳定于运行点1,VSC1功率下降后沿下垂曲线1 移动至运行点2。模式6 启动直流电压恢复的瞬间,d轴外环PI 输入发生阶跃,而后在PI 作用下逐渐收敛于零；在时间轴上,VSC3在t=30 s 时发生功率冲击,然后逐渐稳定；在P-Udc平面上,VSC3由运行点2 经跨度很大的曲线2 收敛于下垂曲线2,再沿下垂曲线2 移动至运行点4。对于模式1,PI 输入的波动幅度远小于模式6,VSC3在P-Udc平面上经跨度很小的曲线1 收敛于下垂曲线3 并于运行点5 达到稳定,对应于时间轴上的P和Udc平稳调至稳态。

3.2.5 新能源出力动态变化时直流电压调节验证

在t=20 s 时,VSC1有功功率波动下降,ADCVC 启动,待系统稳定后启动直流电压调节,系统状态量变化见附录A 图A15 和图A16。

启用ADCVC 的模式1 与模式6 的有功功率变化近乎一致,但直流电压存在显著差别。以VSC3为例,在20～30 s 的动态过程中,模式1 的Udc3始终大于模式6,稳定后2 种模式的Udc3分别为388.07 kV和382.32 kV,相差5.75 kV。无论是动态过程中还是稳定后,启用ADCVC 的模式1 的直流电压均明显大于模式6。

3.2.6 控制策略动作时序验证

在t1=20 s 时,VSC1有功功率从400 MW 下降,t2=22 s 时降至300 MW；t3=30 s 时,第1 轮直流电压恢复启动；t4=32 s 时VSC1有功功率再次下降,t5=34 s 时降至250 MW；t6=38 s 时,第2 轮直流电压恢复启动。不同模式下各VSC 有功功率和直流电压如图5 和图6 所示,其中P1至P4、Udc,1至Udc,4分别为VSC1至VSC4的有功功率和直流电压。

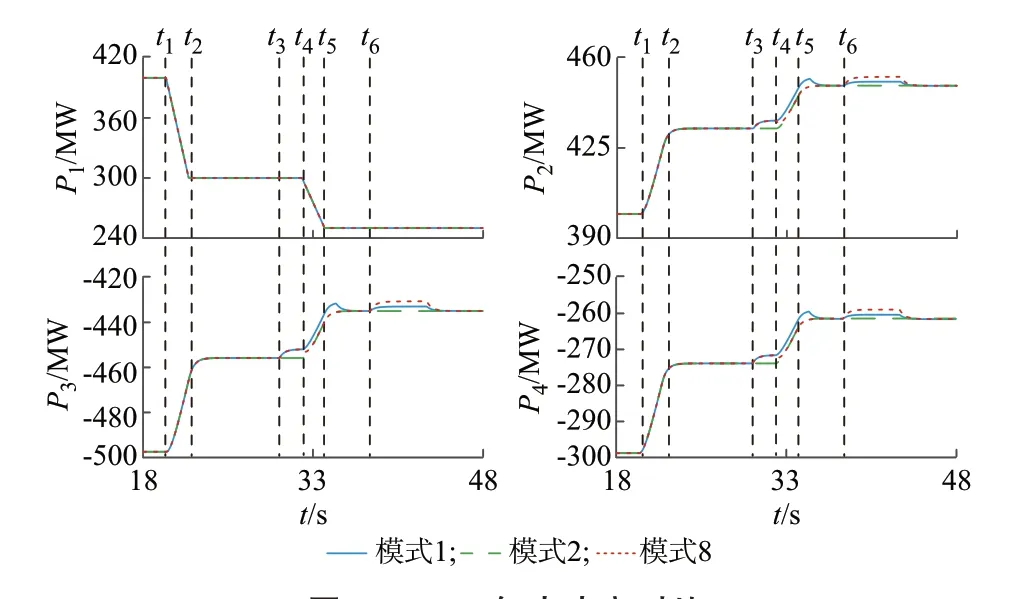
图5 VSC 有功功率对比Fig.5 Comparison of active power of VSCs

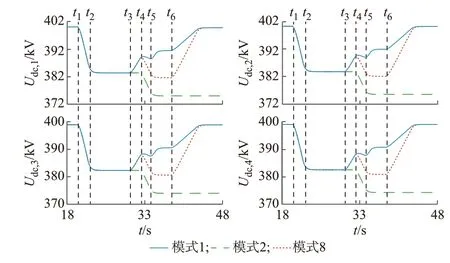
图6 VSC 直流电压对比Fig.6 Comparison of DC voltage of VSCs

模式8 同模式1 在t4之前动作一致,在t4时遭遇VSC1功率二次下跌,模式1 按照预设的第1 轮直流电压恢复过程继续运行,功率参考值继续调整,而模式8 保持t4时的节点有功功率参考值并闭锁第1 轮直流电压恢复。由图5 可知,不同模式下VSC 有功功率的运行轨迹基本一致。由图6 可知,无论是t4～t5的VSC1功率下行阶段,还是t5～t6的新稳态阶段,以及t6后的第2 轮直流电压调节过程,模式1 的Udc均高于模式8。仿真结果表明,本文所提控制动作时序在调压过程中遭遇功率二次下跌时仍可保持较高的直流电压。