考虑电动汽车充放电支撑的配用电系统综合无功优化

2022-03-23姚蓝霓李钦豪杨景旭张勇军

电力系统自动化 2022年6期

姚蓝霓，李钦豪，杨景旭，张勇军

（华南理工大学电力学院,广东省广州市 510640）

0 引言

近年来,电动汽车（electric vehicle,EV）得到迅猛发展,一定程度上缓解了能源短缺危机,但是大规模EV 与电网互动（vehicle-to-grid,V2G）导致节点电压降落,脆弱节点甚至出现电压越下限的情况,严重威胁到电网的安全运行。因此,通过EV 有序充放电等措施来改善电网安全性具有重要意义［1-2］。

目前,通过EV 有序控制削弱EV 充电对配电网的消极影响的研究引起了广泛关注［3-4］。文献［5］在峰谷电价下,通过EV 向电网放电并限制充电功率,有效降低了负荷曲线峰谷差。文献［6］提出一种有序充放电调度分散控制,将充电站集中调度优化问题拆分,提高了计算效率。但是,上述文献在进行有序充放电控制时,往往只考虑EV 与电网之间有功功率的交互,没有充分发挥充电机的无功支撑能力。

近期,已有部分研究通过充电机调度来实现电压或无功功率调控［7-9］。文献［10］分析了充电机的无功补偿能力,从硬件角度提出了控制充电机进行无功补偿的方法。目前,双向充电机技术日益成熟［11-12］,使得EV 和电网之间有功、无功功率的双向交互成为可能,为实现配电网的电压无功特性优化提供了另一种方法。文献［13］通过控制充电机的功率因数,在充电时调节EV 的无功出力,但不涉及放电。双向充电机可以实现四象限运行［14］,而功率因数不能确定无功功率的传输方向,因此不能确定充电机的运行象限。而以功率因数角作为控制变量,可以同时确定有功和无功功率的传输方向及大小,更有利于电网与EV 之间有功和无功功率的双向传输控制。

现有EV 参与无功优化的文献大多从提高电网运行效益的角度,采用电压偏差、网损等传统电网运行指标进行无功优化［15-16］。在这类文献中,EV 通过充电机以无功源的身份参与无功优化,但其无功支撑能力没有得到量化补偿。而国外电力市场发展较为成熟,EV 用户可以在无功辅助市场中报价竞标,或者按V2G 的无功电价计算报酬从而获取收益［17-18］。

在主动配电网背景下,用户与配电网之间的交互逐渐加强［19-20］,而国内尚未建立完善的无功补偿机制。为充分调动用户参与的积极性,不能单方面考虑电网的利益,也要兼顾EV 用户的利益,从而实现综合无功优化。

针对以上不足,本文综合考虑电网侧和用户侧利益,提出一种通过EV 有序充放电实现无功优化的方法。首先,通过控制双向充电机功率因数角实现有功和无功功率双向调控,在此基础上给出有序充放电的控制过程以及功率因数角约束模型；然后,建立无功优化模型,分别为配电网和用户建立需求指标,通过修改充电机状态满足约束条件,并利用粒子群优化（particle swarm optimization,PSO）算法进行求解；最后,通过仿真验证本文模型和方法的有效性。

1 有序充放电控制过程及约束模型

针对大规模无序充电负荷接入配电网造成的电压问题,本文通过优化站内充电机功率因数角控制EV 有序充放电,以改善配电网电压无功特性。

1.1 有序充放电控制过程

当配电网面临电压严重越限而现有无功补偿资源支撑能力不足且EV 调度资源充足时,可通过紧急调度EV 进行有序充放电来填补电压无功补偿的缺口。EV 有序充电控制由电网公司、充电站运营商和EV 用户三方参与,其中电网公司作为调度方主导充电机的功率因数角控制,充电站运营商协助电网公司采集EV 充电信息和控制充电机各时段功率因数角。用户充电主要考虑充电时长和充电费用2 个方面［21］,故可将用户分为2 类：一类用户侧重于追求更短的充电时间,这类用户自接入电网就以额定功率开始充电,直至达到目标电量；另一类用户则追求更低的充电费用,其充电时间相对宽裕,愿意参与有序调控以获得相应的费用补偿。有序充放电控制流程如附录A 图A1 所示。

具体步骤如下：

1）配电网调度中心启动EV 充放电调控机制,下发启动指令到充电站；

2）充电站采集相关信息,包括EV 类型、电池容量等EV 固有属性信息,以及入网时间、离网时间、初始电池荷电状态（state of charge,SOC）、用户参与有序充放电的意愿等用户充电计划信息；

3）各个充电站将采集到的信息上传到配电网调度中心；

4）配电网调度中心通过优化双向充电机各时段的功率因数角,控制入网EV 的充放电行为,从而提高配电网运行的经济性和安全性,同时减少EV 用户花费；

5）配电网调度中心将优化结果下发给各个充电站；

6）充电站依据下发的控制信息,控制站内充电机运行。

1.2 双向充电机状态约束模型

本文通过调整充电机功率因数角控制EV 和电网之间的有功和无功功率的交互。充电机的容量曲线如图1 所示［14］。其中：ωmax为充电机的最大功率因数；φmin和φmax分别为充电机的最小和最大功率因数角。

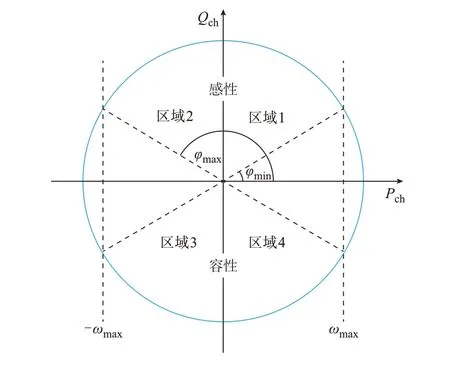
图1 双向充电机容量曲线Fig.1 Capacity curve of bidirectional charger

式中：SL和SH分别为SOC 值的下限和上限；St为t时段的SOC 值。此处取SL=0.20、SH=0.95［22］,当电池充放电深度超过限值时将会减少电池循环次数。

2）车主充电目标约束

车主的充电目标是SOC 达到目标值,而在用户参与有序调控的时间内难以同时满足每个用户对于目标SOC 的要求。为满足EV 用户的出行需求,将用户参与有序调控后的SOC 下限Sla设为：

为满足上述约束,本文将充电过程分为充电前期和充电后期2 个阶段。电池SOC 在充电前期受式（2）和式（5）约束,充电后期受式（4）和式（5）约束。当EV 电池的SOC 进入车主充电目标约束区间时,充电阶段由前期转入后期。定义t时段充电机状态变量Ech,t为：

1.3 电网运行约束

在本文模型中,需要满足以下电网运行约束,其中：式（10）、式（11）为充电机充电负荷与电网的耦合约束；式（12）为购电约束；式（13）为潮流约束。

2 基于有序充放电调度的无功优化模型

有序充放电过程需要各参与方合作,任何一方响应程度不足或积极性不高都会导致有序充放电控制效果不佳甚至失败。因此,综合考虑各方需求是保证有序充放电顺利进行的关键。

2.1 有序充放电各方需求

2.1.1 有序充放电各方需求概述

在利用EV 有序充放电进行无功优化的过程中,会涉及调控方和被调控方2 个方面的利益,调控方即为配电网调控中心,被调控方即为EV 用户。电网公司进行电压无功优化的诉求即为维护配电网运行的安全性和经济性。EV 用户则希望通过参与有序充放电实现收益的最大化,从而最大限度地抵消充电费用。

有序充放电调度过程还涉及充电站运营商的利益。本文设定运营商的利益由电网公司和运营商通过签订合约协调处理,而双方之间的利益分配问题本文不予考虑。

2.1.2 EV 用户需求指标

EV 用户的充电需求主要考虑2 个方面：花费费用最少以及充电结束后的SOC 满足出行需求。

1）充电支出

充电电价包括电网电价和服务电价2 个部分,采用分时费用的形式。EV 用户的充电费用C1可由各时段的费用累加得到：

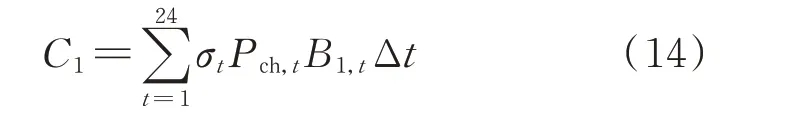
式中：B1,t为t时段的充电电价；σt为t时段充电状态标记因子,当Pch,t≥0 时σt=1,Pch,t＜0 时σt=0；Δt为单位时段时长。

2）放电收入

上网电价高于充电电价时EV 用户由此盈利。因此,EV 用户的放电收入C2为：

4）无功优化补贴

无功优化带来的网损下降效益体现在购电量减小上。本文将购电量减小带来的效益分给参与无功优化的EV 用户,即

式中：τ为无功状态标记因子,当Qch,t＜0 时τ为1,否则为0。

5）期望SOC 偏差值

通过定义期望SOC 偏差值来反映EV 用户对充电后实际SOC 的满意度。期望SOC 满意度Ddev为：

式中：ρEV为EV 用户的需求满足指数,ρEV越小表示EV 需求满足程度越高；β1和β2为权重系数。

采用充电站内所有EV 用户需求满足指数的平均值ρs来代表充电站EV 用户的群体需求,即

式中：ρEV,n为充电站内第n辆EV 的需求满足指数；Ns为充电站内EV 的数量。

2.1.3 配电网运行指标

为更好地满足配电网的运行需求,本文结合电压偏差和网损2 个指标来考察有序充放电控制过程中配电网经济性和安全性的改善效果。

1）最大电压偏差率

配电网节点电压越限会严重危害配电网运行的安全性。一定规模的EV 负荷接入配电网电压脆弱点,在负荷峰值时段极易引起电压越下限。因此,将电压偏差率作为指标来帮助改善电压曲线,即

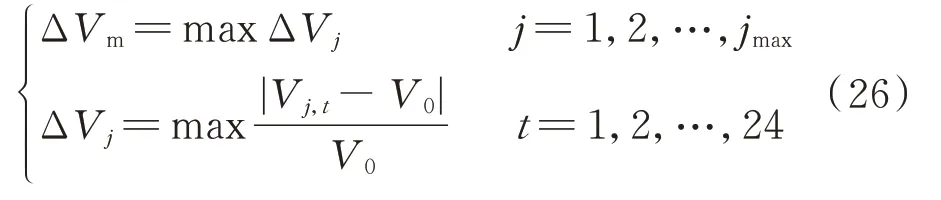
式中：ΔVm为最大电压偏差率；Vj,t为t时段节点j的电压幅值；jmax为节点数；ΔVj为节点j在24 个时段内的最大电压偏差率；V0为目标电压,可设定为1。

2）配电网网损下降率

配电网网损反映了电网运行的经济性,因此可建立网损下降率指标。线路网损为：

式中：β3和β4为加权系数。

4）综合目标指数

为协调EV 用户和配电网运行的需求,本文综合EV 用户平均需求满足指数和配电网需求满足指数,建立综合目标指数χ代表EV 用户和配电网的综合利益,即

综合目标指数越小则EV 用户和配电网的综合利益越高。因此,有序充放电模型的目标函数为：

2.2 基于PSO 算法的充电机功率因数角优化

本文选取PSO 算法对充电机功率因数角进行优化,粒子位置为各充电机在各时段的功率因数角。每个粒子包含2 个状态信息,分别为代表解空间内一个可行解的粒子“位置”和决定下次迭代更新步长的粒子“速度”,更新公式分别如下：

假设所有充电站的总充电机数量为Ms,以1 h为单位优化时段,则粒子“位置矩阵”为：

式中：Vm,t为粒子速度的(m,t)维分量。

优化流程如附录A 图A2 所示。在每一次迭代过程中,都需根据粒子当前位置判断是否满足SOC约束,不满足约束时,按照充电机所处充电阶段对充电机状态进行修正,然后计算充电机状态修正后的各个粒子的适应度值,即综合目标指数,从而更新个体和群体极值信息以及粒子位置和速度,继续迭代直至输出最优解。

3 算例分析

3.1 仿真参数设置

本文采用IEEE 33 节点模型进行仿真分析,节点模型如附录B 图B1 所示。EV 电池容量为50 kW·h,实际续航里程为200 km,为方便计算,设定电池损耗费用为0.415 元/（kW·h）。设定充电机容量为7 kW,最大功率因数取值为0.95［26］,对应最小和最大的功率因数角分别为18.2°和161.8°。分别在节点8、16 和32 处接入充电站。常规负荷的日负荷曲线如附录B 图B2 所示,期望峰值总和取4 MW,变异系数为0.3［27］。在仿真过程中,各用户的起始SOC、到站时间等充电信息通过附录B 表B1中的用户出行和充电行为的概率分布抽样得到。充电站参数如附录B 表B1 所示,充放电电价如附录B图B3 所示。配电网电压等级为10 kV,购电电价为0.426 元/（kW·h）。其余仿真参数如附录B 表B2 所示,其中,在确定综合目标指数的权重时平等考虑各充电站权益,因此α1、α2、α3取值相等,并且在调试中发现配电网需求满足指数的趋优灵敏度远低于用户需求满足指数,为平衡各方利益,γ1、γ2分别设为1和100。

3.2 配电网电压与网损分析

3.2.1 配电网电压优化分析

设定用户参与充放电的比例为50%、75% 和100%,分别绘制接入充电站的节点在无EV 接入、EV 无序充电（以最大功率因数运行）和不同响应比例下的电压曲线。节点32 的电压曲线如图2 所示,其余节点的电压曲线如附录C 图C1、图C2 所示。

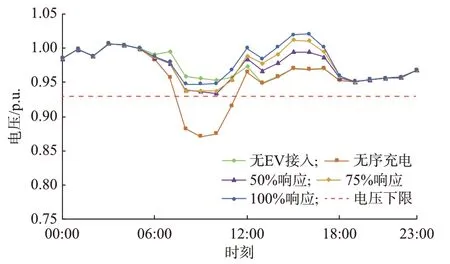
图2 节点32 的电压曲线Fig.2 Voltage curves of node 32

当接入充电负荷后,3 个节点都出现电压越下限的现象。其中,节点8 在09：00—11：00 时段内电压低于下限。节点16 和节点32 位于网络靠后位置,在08：00—12：00 时段内的电压下降到0.93 p.u.以下,08：00—11：00 时段电压严重越下限,威胁到配电网安全运行。

根据本文的有序充放电方法对3 个充电站内的EV 进行调控之后,电压曲线抬升效果明显,50%响应下电压曲线也能基本抬升至0.93 p.u.以上,电压曲线更加平缓,大大降低了节点电压越下限的风险。

3.2.2 充电站功率优化分析

以75%响应下的1 号充电站为例进行分析,充电站有序充放电前后的功率曲线如图3 所示。结果显示,有序充放电后07：00—10：00 时段内的有功功率下降明显,部分充电负荷被转移到下午时段。在调控手段的作用下,在馈送无功功率和有功功率峰值削减的双重作用下,节点电压抬升,大大降低了配电网电压的越限风险。

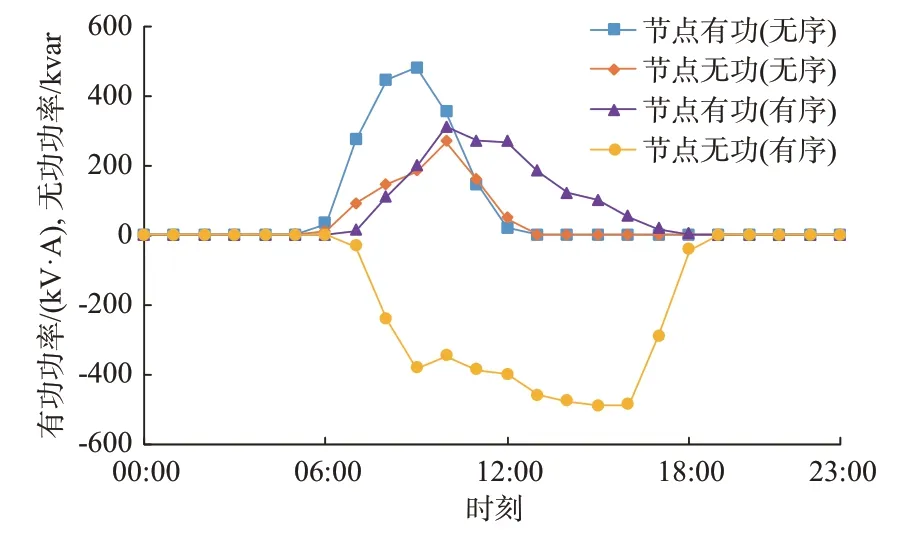
图3 1 号充电站的有功和无功功率Fig.3 Active and reactive power of No.1 charging station

3.2.3 配电网网损优化分析

各场景的网损优化结果如图4 所示。EV 接入电网进行无序充电后,配电网网损率从7.85%上升至10.14%,但是经过优化之后,50%响应程度下网损率回降到7.89%,接近未接入EV 时的网损率,网损下降率达到22.19%,下降效果明显。在用户响应程度较高时,网损率将得到进一步的改善,甚至优于无EV 接入时的情景,75%响应和100%响应下的网损下降率分别达到28.11%和38.07%。

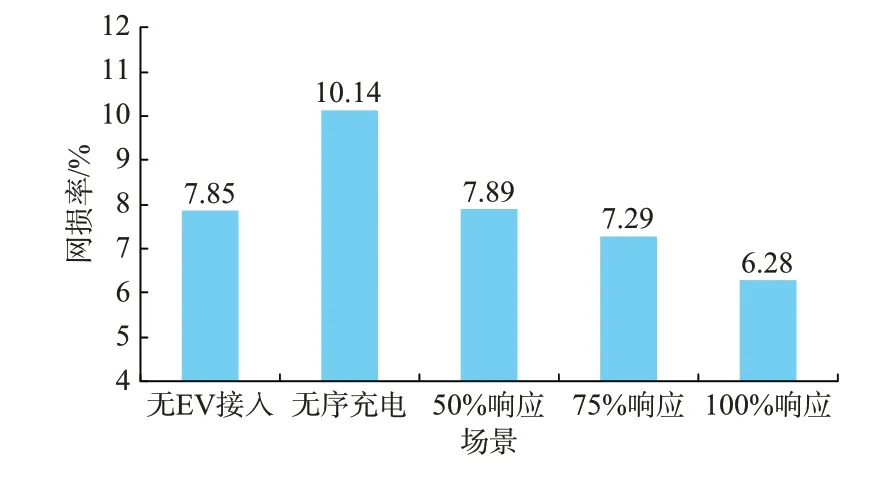
图4 各场景下的配电网网损率Fig.4 Loss rate of distribution network in each scenario

3.2.4 优化效益分析

为分析本文所提方法的有效性,将优化结果与电容器补偿结果进行对比。分别在各个充电站所在节点接入电容器补偿装置,单组电容器容量为0.1 MW,各节点电容器组数均为4 组。

表1 对比了75%响应以及电容器补偿在不同启动次数下的成本。本文所提策略的成本主要体现在对用户的放电和无功补贴上,而电容器补偿的成本主要是设备固定成本,两者的收益均为网损下降带来的购电成本下降。表中结果显示,当启动次数为10 次/a 时,两者的年成本较为接近,启动次数低于10 次/a 时采用本文的策略更为经济,而高于10 次/a时采用电容器补偿更为合适。因此,本文所提策略更加适用于紧急情况下的运行优化,若需进行常态的无功补偿,应采用电容器这类常规补偿方法。

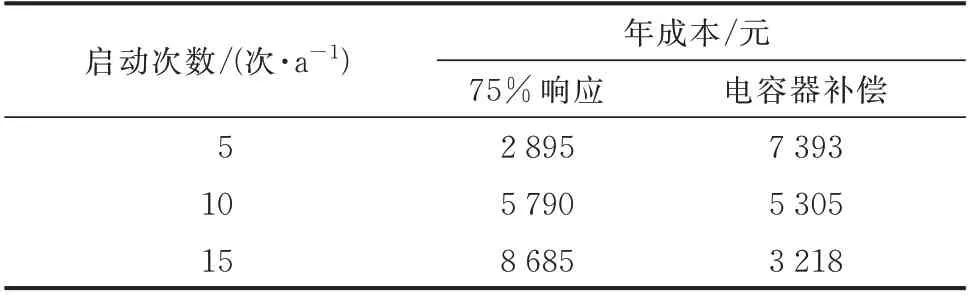
表1 不同补偿方法下的年成本Table 1 Annual costs with different compensation methods

另一方面,以节点16 为例,不同补偿方式下节点16 的电压曲线如图5 所示。结果显示,电容器补偿下的节点电压出现越下限的情况,而且有序充放电下的电压曲线改善效果更加明显。由于电容器组只能分组投入,因此无功补偿量具有不连续性和滞后性,而本文所提方法可以依据电网运行状况调整补偿量,从而实现连续补偿。除此之外,本文所提的有序充放电方法在网损优化方面也优于电容器补偿。电容器补偿带来的网损下降率为11.83%,而有序充放电为28.11%,较电容器补偿高出11.68%。因此,相比于电容器补偿方法,本文方法在改善电网安全性和经济性方面具有优越性,可作为一种较为可靠的无功补偿方法辅助电网进行无功优化。

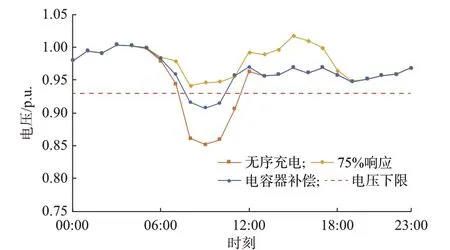
图5 不同补偿方法下节点16 的电压曲线Fig.5 Voltage curves of node 16 with different compensation methods

3.3 用户利益分析

充电站用户支出和各项收入花费明细分别如附录C 表C1、表C2 所示。对3 座充电站内接入的EV负荷进行调控之后,站内EV 用户的平均花费平均下降15.96%,优惠力度显著,可以激励用户积极通过参与配电网有序充放电进行调控。从表中看出,用户通过向电网放电和提供无功补偿服务获得收入,从而降低了充电总花费。

3.4 用户临时用车需求分析

在实际生活中,可能会有部分EV 用户在充电过程中产生临时用车的需求,有序充放电可能会对用户临时用车需求产生影响。因此,本节通过随机抽取用户产生临时需求、设置出行距离分布来考察EV 电量满足出行需求的概率。

假设20%的EV 产生临时需求,临时用车时间在接入电网到离开电网的时段内随机抽取,临时出行距离参数满足正态分布,设置不同的临时出行距离分布,模拟用户临时出行行为,考察出行需求满足率,得到结果如表2 所示。表中,临时出行距离的单位为km。

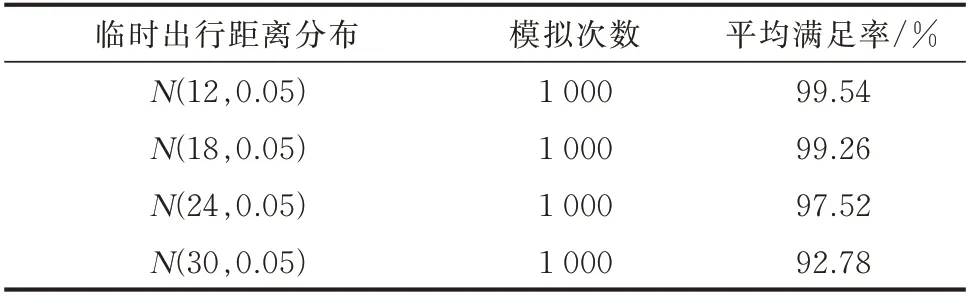
表2 出行需求满足率对比Table 2 Comparison of satisfaction rate of travel demand

随着临时出行距离的增大,用户临时出行满足率在不断下降,但当临时出行距离较近时,用户的临时出行需求满足率接近100%,绝大多数的出行需求都能得到满足。对于临时出行距离较远的用户,是否参与本文所提的有序充放电活动需要慎重考虑。总之,鉴于大部分用户的临时出行距离都较近,本文控制方法能够满足绝大多数用户的临时出行需求,对用户出行需求的影响较小。

除以上仿真之外,本文还对PSO 算法的稳定性进行了分析,具体分析内容见附录D。