基于知识和数据联合驱动的并网逆变器多工况阻抗获取方法

2022-03-23吴滨源李建文李永刚刘淇玉杨夷南

电力系统自动化 2022年6期

吴滨源，李建文，李永刚，王月，刘淇玉，杨夷南

（1. 新能源电力系统国家重点实验室（华北电力大学）,河北省保定市 071003；2. 国网安徽省电力公司肥东县供电公司,安徽省合肥市 231600）

0 引言

随着碳达峰和碳中和目标的提出与逐步实施,电力电子化新能源电力系统正在加速形成［1-2］。作为连接清洁能源和电网的关键设备,并网逆变器大量接入电网,使得次/超同步振荡和谐波谐振等谐波不稳定问题凸显,给电力系统的安全稳定运行带来新的挑战［3］。并网逆变器阻抗的准确获取是进行谐波稳定性分析［4］的关键前提之一,常用的阻抗获取方法基于知识驱动,可分为白箱机理建模和黑/灰箱测量2 种方法［5］。

白箱机理建模方法包括状态空间平均法［6］、dq模型方法［7］、动态相量法［8］、谐波线性化方法［9］、谐波状态空间分析方法［10］等。文献［11］对这些方法进行了总结对比,认为dq模型方法更具广泛性和普适性。由于dq模型往往表现为传递函数矩阵的形式,因此该模型只能表征并网逆变器在特定运行工况下的阻抗特征。为了对并网逆变器的多工况阻抗特性进行研究,文献［12］通过权重函数对不同工况下的小信号模型进行线性组合。文献［13］将工况变化转化为扰动函数,建立了大信号阻抗模型。文献［14］对考虑频率耦合效应的变流器系统进行了全工况阻抗建模。然而,实际工程现场中存在大量结构、参数、控制方式等内部信息保密的商用逆变器,上述白箱机理建模方法存在应用推广上的困难。

黑/灰箱测量方法无需并网逆变器内部保密信息,因此受到广泛关注。这类方法的基本原理是：在逆变器并网点串联接入电压扰动源或并联接入电流扰动源,电压/电流扰动经逆变器回路产生电流/电压响应,采集并网逆变器端口电压及电流数据,计算得到相应阻抗值。文献［15］对电压扰动和电流扰动的适用性进行了对比。文献［16］通过注入扰动对运行工作点的解耦模型参数进行辨识。文献［17］基于阻抗测量方法对多逆变器系统稳定性进行了校验。黑箱或灰箱测量方法虽然克服了白箱机理建模的应用缺陷,但在实际工程现场中,并网逆变器运行工况总会随电网需求发生变动,这类方法虽然可以实时获取dq阻抗数据,但是需向运行中电网持续注入谐波电流或电压扰动,因此会影响电网的正常运行,并带来额外的谐波污染。

近年来,以机器学习为代表的人工智能技术快速发展,能源行业的数字化趋势［18］为其在电力研究中的应用创造了条件。基于数据驱动的机器学习模型具有较好拟合输入输出变量间非线性关系的优点,已成功应用于负荷或新能源预测［19-20］、系统模式识别［21］等诸多领域。并网逆变器多工况dq阻抗与逆变器外部测量变量间存在复杂的非线性关系,这一特点与机器学习模型的优势相契合。文献［22］建立了一种反向传播神经网络（back propagation neural network,BPNN）模型,为获取并网逆变器多工况dq阻抗提供了新的思路。然而该文献存在以下不足：1）由于缺乏对先验知识的理解,所给出的模型输入变量缺乏解释性；2）BPNN 模型本身超参数设置复杂,泛化能力弱。

基于上述分析,本文提出一种基于知识和数据联合驱动的阻抗获取方法。首先,以L 型和LCL 型并网逆变器典型拓扑为例,基于知识驱动进行小信号白箱机理建模,分析与多工况dq阻抗存在非线性关系的变量；然后,借助MATLAB/Simulink 仿真平台搭建仿真模型获取大数据,并训练遗传算法优化核极限学习机（genetic algorithm-kernel extreme learning machine,GA-KELM）,实现并网逆变器多工况dq阻抗的准确获取。

1 基于知识驱动的输入变量分析

与并网逆变器多工况dq阻抗相关的变量包括并网逆变器并网点电压、并网支路电流、逆变器输出功率等。选取GA-KELM 的输入变量时,可通过数据降维、聚类等方法［19-20］进行筛选。然而这类方法过于依赖数据样本的规模和质量,选取结果往往缺乏解释性。针对这一缺陷,本文首先基于知识驱动,以L 型和LCL 型并网逆变器典型拓扑为例,通过小信号白箱机理建模,实现GA-KELM 输入变量的合理选取,具体原理说明如下。

1.1 L 型并网逆变器

附录A 图A1 为L 型并网逆变器典型拓扑,该拓扑的小信号框图如图1 所示［23］。

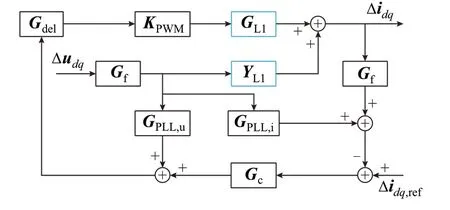
图1 L 型并网逆变器小信号框图Fig.1 Small-signal block diagram of L-type grid-connected inverter

图1 中：Δidq为并网电流d轴和q轴分量小信号；Δidq,ref为并网电流d轴和q轴分量参考值小信号；Δudq为并网电压小信号；KPWM为脉宽调制（pulse width modulation,PWM）增益矩阵；YL1为L 型滤波器组导纳矩阵；GL1为YL1与负单位矩阵的乘积；Gc为电流环比例-积分（proportional-integral,PI）控制器传递函数矩阵；GPLL,u和GPLL,i分别为锁相环（phase locked loop,PLL）锁相误差对电压和电流控制环节影响的传递函数矩阵；Gdel为控制延时环节传递函数矩阵；Gf为采样滤波器传递函数矩阵［24］。上述各变量具体表达式如附录A 式（A1）所示。根据图1 得到并网逆变器dq导纳矩阵YL（s）表达式如式（1）所示。

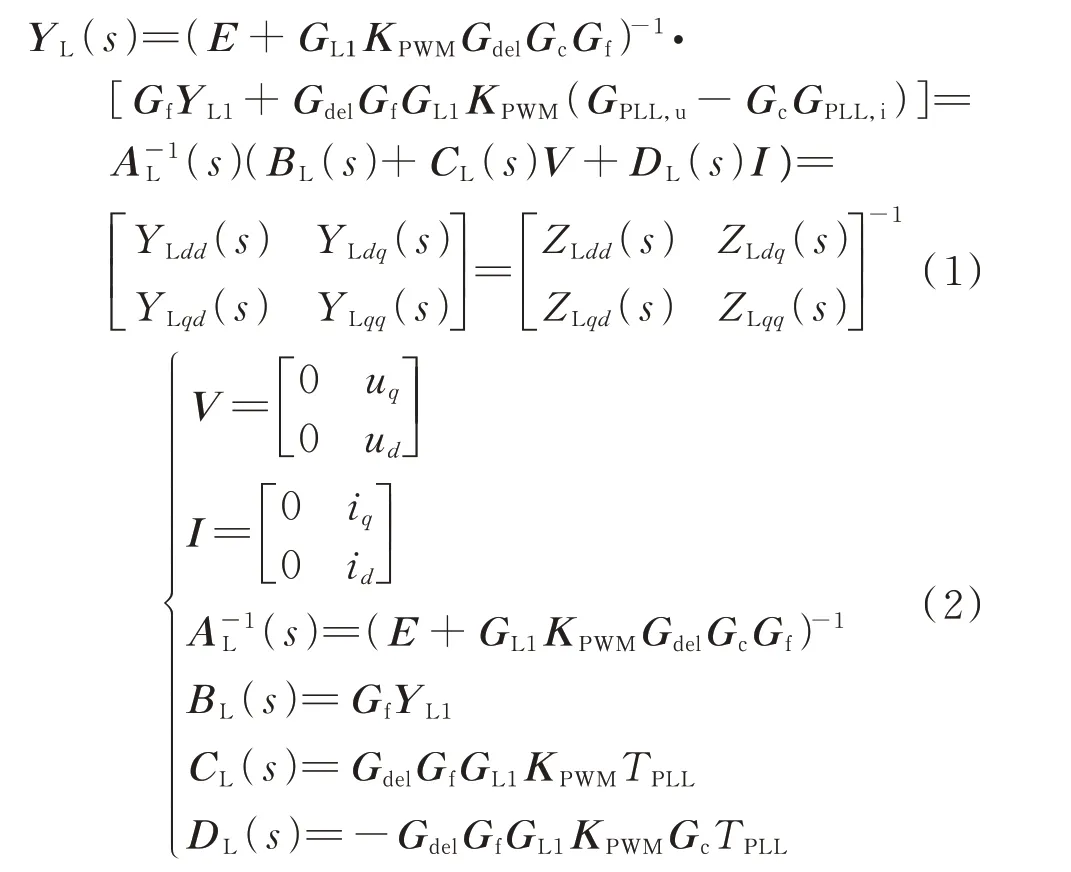
式中：s=jω=j（2πf）,其中f为频率,ω为角频率；E为2×2 单位矩阵；V和I分别为电压和电流矩阵；AL(s)、BL(s)、CL(s)、DL(s)分别为相应的系数矩阵；YLdd(s)、YLdq(s)、YLqd(s)、YLqq(s)以及ZLdd(s)、ZLdq(s)、ZLqd(s)、ZLqq(s)分别为L 型并网逆变器导纳和阻抗在dd通道、dq通道、qd通道、qq通道的相应元素；TPLL为PLL 传递函数,具体表达式如附录A式（A1）所示；id和iq分别为并网电流d轴分量和q轴分量；ud和uq分别为并网电压的d轴和q轴分量。整理式（1）可得式（3）所示等式。结合s与f之间的线性关系,阻抗Z与导纳Y间的倒数关系,对式（3）进行整理后可以看出：L 型并网逆变器dq阻抗均可由式（4）所示函数进行统一表示。

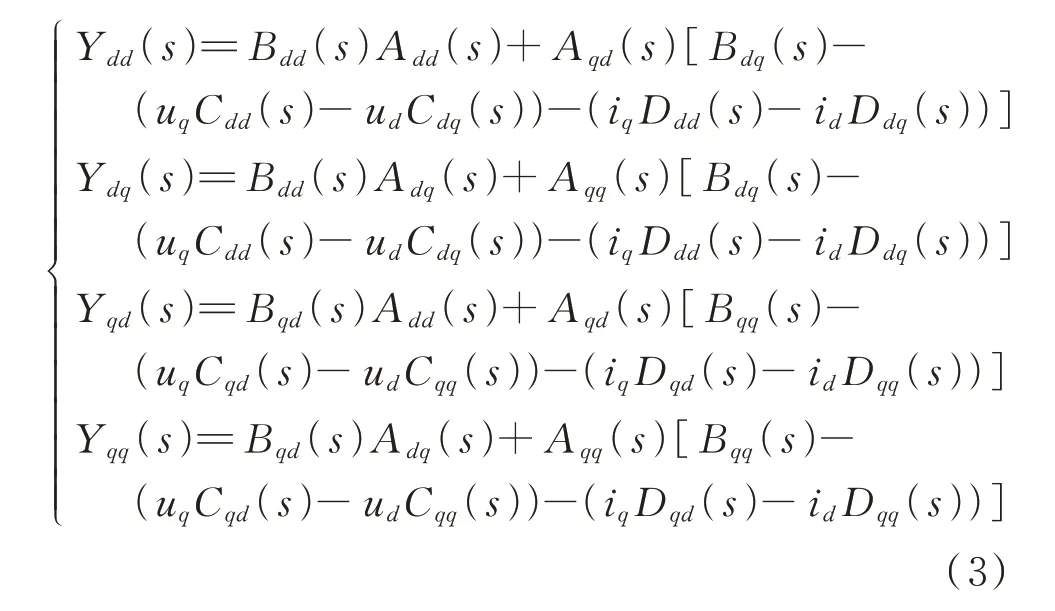
式中：Add(s)、Adq(s)、Aqd(s)、Aqq(s)、Bdd(s)、Bdq(s)、Bqd(s)、Bqq(s)、Cdd(s)、Cdq(s)、Cqd(s)、Cqq(s)、Ddd(s)、Ddq(s)、Dqd(s)、Dqq(s)分别为相应系数矩阵AL(s)、BL(s)、CL(s)、DL(s)在dd通道、dq通道、qd通道、qq通道的相应元素。

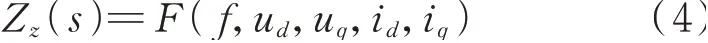
式中：F（·）为输入变量f、ud、uq、id、iq与输出变量Zz(s)（z=dd,dq,qd,qq)之间的非线性关系函数,其含义为给定输入变量ud、uq、id、iq、f后,通过该函数能够得到输出变量Zdd（s）、Zdq（s）、Zqd（s）、Zqq（s）。

1.2 LCL 型并网逆变器

附录A 图A2 为LCL 型并网逆变器典型拓扑［25］,该拓扑的小信号框图如图2 所示。

图中：ΔiCdq为电容支路电流d轴分量和q轴分量小信号；A1至A6、B1、C1为系数矩阵,具体表达式如附录A 式（A2）所示。

根据图2 所示的小信号框图得LCL 型并网逆变器dq导纳YLCL（s）表达式如式（5）所示。

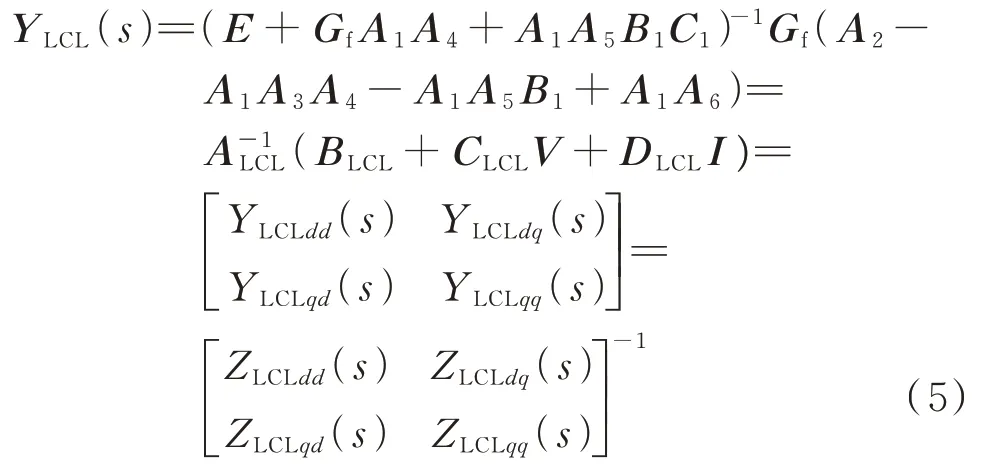
式中：YLCLdd(s)、YLCLdq(s)、YLCLqd(s)、YLCLqq(s)、ZLCLdd(s)、ZLCLdq(s)、ZLCLqd(s)、ZLCLqq(s)分别为LCL型并网逆变器导纳和阻抗在dd通道、dq通道、qd通道、qq通道的相应元素；ALCL、BLCL、CLCL、DLCL分别为相应的系数矩阵。

参考L 型并网逆变器的推导过程,经计算整理后发现：LCL 型并网逆变器阻抗也可以由式（4）所示函数进行统一表示。

从上述分析中可以看出：并网逆变器多工况dq阻抗总存在式（4）所示的非线性关系,对于本文未列举的其他拓扑或控制方式的并网逆变器也适用。

2 阻抗获取模型的建立

GA-KELM 是一种以单隐含层前馈神经网络为主要架构的机器学习模型,相较于文献［22］提出的BPNN 模型,不仅能较快且较准确地学习多输入多输出变量间的复杂非线性关系,而且具有泛化能力强、超参数设置简单等优点［26-27］。工程现场中为保证后续谐波稳定性分析结论的准确性和实效性,并网逆变器多工况dq阻抗应具备精确性和及时性。因此,结合实际应用特点,本文选用GA-KELM 对并网逆变器多工况dq阻抗进行求解。

2.1 核极限学习机

根据本文第1 章基于知识驱动的模型输入变量分析结果,建立图3 所示极限学习机基础模型。

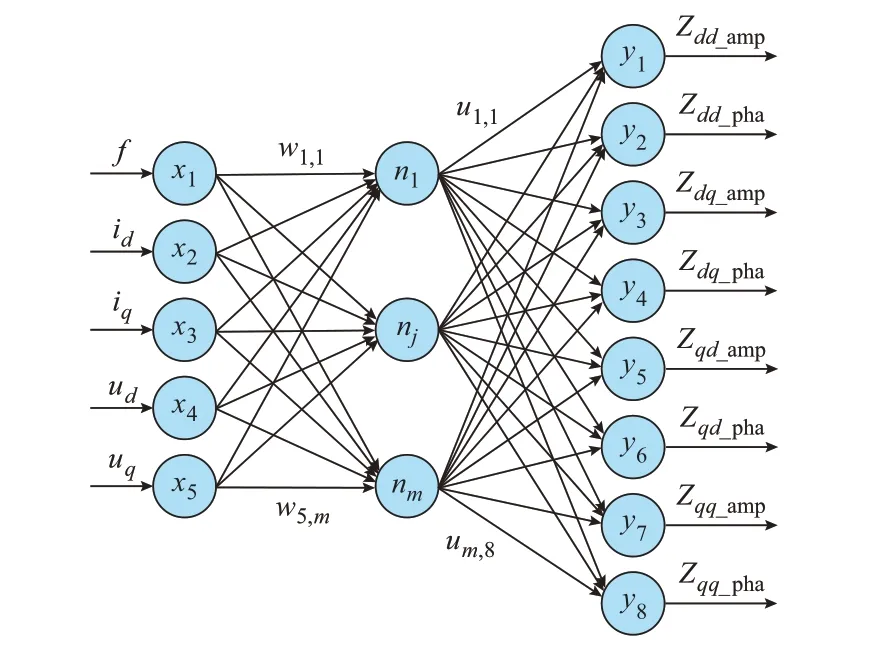
图3 极限学习机基础模型Fig.3 Basic model of extreme learning machine

图中,x1,x2,…,x5为输入节点；n1,n2,…,nm为隐藏节点；m为隐含层节点数；y1,y2,…,y8为输出节点；W=［ws,1,ws,2,…,ws,m］为输入权重向量,s=1,2,…,5；U=［u1,1,u1,2,…,um,r］为输出权重向量,r=1,2,…,8；下标中amp 和pha 分别表示阻抗幅值和阻抗相角。

假设通过P组训练样本{（Xi,Yi）}（i=1,2,…,P）对图3 所示模型进行训练,其中,Xi=［xi1,xi2,…,xi5］T=［fi,iid,iiq,uid,uiq］T,为输入样本；Yi=［yi1,yi2,…,yi8］T=［Zdd_ampi,Zdd_phai,Zdq_ampi,Zdq_phai,Zqd_ampi,Zqd_phai,Zqq_ampi,Zqq_phai］T,为输出样本。经训练后,第i个样本模型的第r个输出节点的输出值y′ir如式（6）所示。

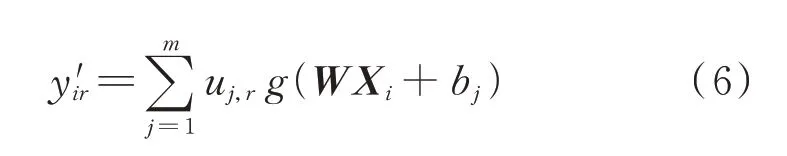
式中：uj,r为第j层隐含层第r个输出节点的权重；g（·）为激活函数；bj为第j层隐含层的偏置项。

模型训练的理想结果是模型任意输出节点的输出值能够零误差地逼近P个样本的实际值,即

式中：H为模型隐含层输出矩阵；Y′为输出矩阵。

根据线性系统最小二乘解理论,存在最优输出权值U*使式（8）成立［26］,此时U*=H+Y′,其中H+表示矩阵H的Moore-Penrose 广义逆,根据H+=（HHT）-1进行求解。

模型实际训练过程中,由于并网逆变器dq阻抗样本数往往远大于隐含层节点数,因此样本间存在复共线性问题［27］,此时HHT奇异,直接导致模型每次训练得到的输出权值波动,模型泛化性不足。针对这一问题,本文引入核函数Ψ替代HHT,从而建立起核极限学习机模型,如式（10）所示。

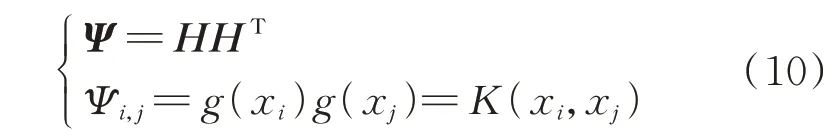
式中：K(xi,xj)=exp(-(xi-x2j/σ)),为核函数,其中σ为幅宽。

根据文献［26］,由于核函数采用了内积的计算方式,因此模型隐含层节点数及其初始偏置不必特别设定和讨论。

2.2 遗传算法优化

尽管核极限学习机与极限学习机相比具有较高的泛化性,但其输入权值仍存在随机性大的问题。针对这一缺陷,本文采用遗传算法对核极限学习机的输入权值进行优化,从而建立起完整的GAKELM 模型,进一步增强模型的泛化性,优化计算流程如附录B 图B1 所示。具体说明如下。

1）待确定的遗传算法基本参数包括：遗传算法的最大遗传代数、种群大小、个体长度、代沟、交叉概率和变异概率。

2）核极限学习机的输入权值与种群中的个体相对应,采用实数进行编码。

3）通过GA-KELM 获取的阻抗输出值与阻抗实际值间通过式（11）计算均方根误差（root mean square error,RMSE）εRMSE,该误差的大小直接反映了所建模型的精度优劣。

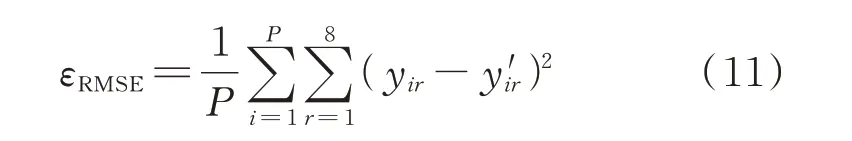
4）选择、交叉和变异分别采用轮盘赌法、多点交叉和随机选取变异点的方法。

5）终止条件是指是否到达最大遗传代数。

3 阻抗获取方法实施流程

本文提出一种基于知识和数据联合驱动的并网逆变器多工况dq阻抗获取方法,该方法的具体实施流程如附录B 图B2 所示,包括数据获取、模型建立、误差校验3 个主要步骤。

步骤1：数据获取。GA-KELM 模型的精确建立需以并网逆变器多工况dq阻抗大数据为基础。然而,实际工程现场中相关数据较为稀缺。针对这一问题,本文参考文献［22,28-29］,在MATLAB/Simulink 中搭建仿真模型,通过改变控制回路中电流参考值及并网点电压实现并网逆变器的工况改变,利用软件中的阻抗扫描模块实现并网逆变器多工况dq阻抗大数据的获取。

步骤2：模型建立。以第1 章基于知识驱动分析得到的变量为输入、并网逆变器dq阻抗为输出建立核极限学习机模型,利用遗传算法对核极限学习机输入权值进行优化。为保证模型训练效果,本文参考文献［5］,对步骤1 得到的数据集进行五折交叉检验。

步骤3：误差校验。基于RT-LAB 搭建半实物实时仿真平台,基于扰动注入法［15-17］对不同工况下的并网逆变器dq阻抗进行测量计算,形成测试数据集。其中,扰动注入法具体流程如附录B 图B3 所示,阻抗计算结果如式（12）所示。

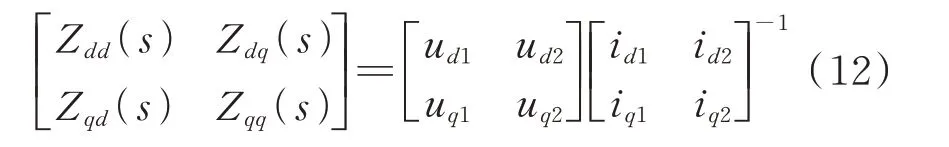
式中：下标1 和2 分别表示第1 次、第2 次扰动注入。

根据文献［15］,本文采用扰动电压源串联接入的方式对并网逆变器多工况dq阻抗进行测量,扰动信号为正弦波［16］,扰动注入示意图如附录B 图B4 所示（以LCL 型并网逆变器为例）。考虑PLL 的动态影响,本文实验中每次扰动仅注入单一频率的信号［16］。注入信号的幅值不应过大,否则将改变并网逆变器的运行工况；也不应过小,避免无法产生准确的电流响应,因此结合文献［30-31］,经综合考虑后本文确定采用逆变器并网电压有效值的5%。

4 算例分析

4.1 实验基本参数说明

参考附录A 图A2 给出的LCL 型并网逆变器典型拓扑,本文首先在MATLAB/Simulink 中搭建并网逆变器仿真模型。其中,上位机处理器参数为：2.5 GHz Intel Core i5,仿真模型参数为：直流侧电压Vdc为720 V；电网电压ug幅值为311 V；电网基波频率f1为50 Hz；开关频率fr为10 kHz；逆变器侧电感L1为0.6 mH；滤波电容C1为10 μ F；网侧电感L2为0.15 mH；锁相环比例系数kppll为0.2；锁相环积分系数kipll为45；并网电流反馈比例系数kpi为0.45；并网电流反馈积分系数kii为1 000；有源阻尼系数kc为1.15。

通过MATLAB/Simulink 仿真模型生成训练GA-KELM 模型所需的大数据。其中,输入变量ud、uq、id、iq、f的变化范围设置如下：在基于电网电压定向的同步旋转坐标系中,ud=ug,uq=0,考虑电网电压一般在0.95ug～1.05ug范围内波动,因此ud取295～326 V,步长为1 V。并网逆变器dq轴电流参考值id和iq变化范围为50～90 A 和0～40 A,步长均为1 A。当iq=0 时,并网逆变器工作于单位功率因数状态；当id=90 A,iq=40 A 时,并网逆变器工作在最大有功功率、无功功率输出状态。f变化范围根据实际现场受关注的频率范围决定,本文设置为10～1 000 Hz,步长为10 Hz。输出变量（并网逆变器多工况dq阻抗）通过阻抗扫描模块进行采集。经统计,共产生LCL 型并网逆变器多工况dq阻抗有效样本5 379 200 个。

利用上述样本对GA-KELM 模型进行训练。其中,核极限学习机输入权值通过遗传算法进行优化,遗传算法主要参数设置如下：最大遗传代数为40；种群大小为30；个体长度为20；迭代间隙为0.95；交叉概率为0.7；变异概率为0.01。以εRMSE作为适应度值,绘制出模型优化过程中的适应度变化曲线如附录C 图C1 所示。从图中可以看出：当种群进化到30 代时,适应度达到较小值,随代数的增加适应度减小幅度变化不大,这说明本文设置的遗传算法参数是合理有效的,核极限学习机可以通过遗传算法获取到全局最优的输入权值。待模型达到最大遗传代数后,对最优个体进行解码,GA-KELM 模型训练完成。

基于RT-LAB 搭建半实物实时仿真平台,平台示意图如附录C 图C2 所示。其中,上位机与前文在MATLAB/Simulink 中搭建并网逆变器仿真模型的上位机一致,实时仿真器型号为OP5600。为保证实验结果的可视化和可重复性,基于本文方法,采用扰动注入法对测试工况下并网逆变器dq阻抗进行测量,获取模型验证所需的阻抗实际值。

4.2 有效性及优越性分析

利用本文所提方法训练得到的GA-KELM 模型获取测试工况（id=40 A,iq=20 A,ud=ug,uq=0,f=10～1 000 Hz,步长为10 Hz）下并网逆变器dq阻抗,并绘制出阻抗获取结果的Bode 图,如图4所示。

由图4 所得结果可知,一方面,本文通过离线仿真系统得到的训练数据是可靠的；另一方面,通过本文方法可以获得较为准确的并网逆变器多工况阻抗结果。另外,采用本文方法获取的阻抗3 维变化图与通过扰动注入法实际测量得到的阻抗3 维变化图基本一致,阻抗计算平均误差εRMSE为4.382,普遍较小。这都证明了本文方法的有效性。

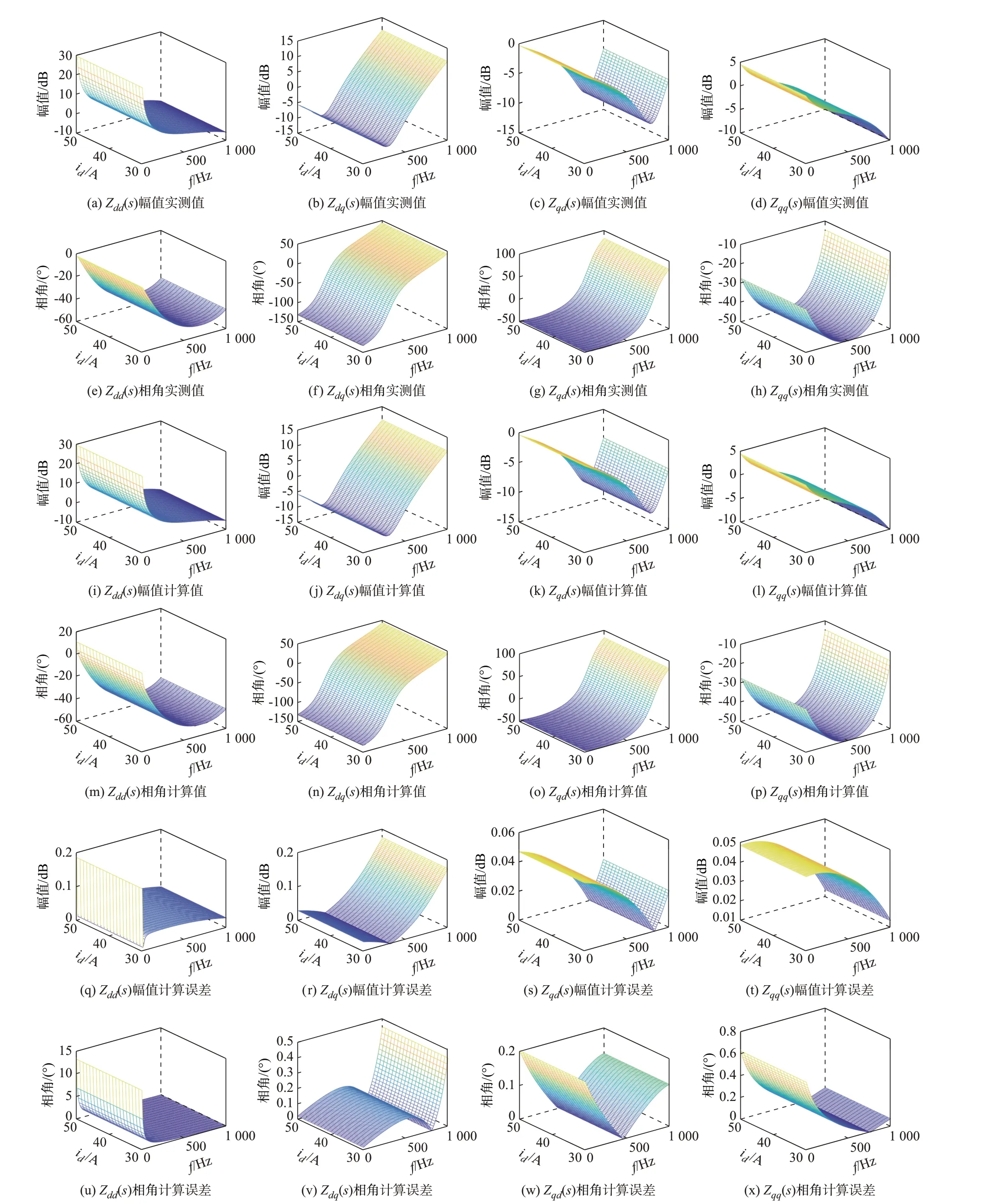
图4 通过GA-KELM 获取的dq 阻抗测试结果Fig.4 Testing results of dq impedance acquired by GA-KELM

为了验证本文方法的优越性,选取未经遗传算法优化的核极限学习机模型［27］、BPNN［22］、卷积神经网络（convolutional neural network,CNN）［29］与GA-KELM（本文方法）进行对比。其中,各模型的输入、输出变量以及核极限学习机、BPNN 模型的隐含层节点数与GA-KELM 保持一致,CNN 卷积核设置为5×5,池化核大小为2×2,所有模型的超参数均随机初始化,训练和验证均采用相同的样本数据集。将上述模型进行训练和验证后,统计各模型的训练样本误差εRMSE_train、训练平均时间ttrain、验证样本误差εRMSE_test、算法程序文件所占存储空间Space（单位KB）、模型对大数据的依赖程度Need（分为低、中、高3 个等级）,如表1 所示。需要说明的是,为了进一步对比各模型阻抗获取的结果,并兼顾数据可视化效果,本文以Zdd（s）为例,绘制出特定工况（id=40 A,iq=20 A,ud=ug,uq=0,f=10～1 000 Hz,步长为10 Hz）下各模型阻抗获取结果的Bode 图如图5所示。

首先,对比各模型的训练样本误差εRMSE_train,从表1 可以看出,4 种模型的训练样本误差普遍较小,且彼此之间相差不大。结果表明,机器学习模型能较好地学习输入变量ud、uq、id、iq、f和输出阻抗变量间的复杂非线性关系,本文提出采用机器学习模型对并网逆变器多工况dq阻抗进行获取的思路是合理有效的。

然后,对比各模型的验证样本误差εRMSE_test,从表1 可以看出,GA-KELM 的验证样本误差εRMSE_test与CNN 误差相近,小于核极限学习机和BPNN。从图5 可以看出,GA-KELM 模型获取结果和CNN 模型获取结果与实测值接近重叠,核极限学习机模型获取结果和BPNN 模型获取结果与实测值相差较大。结果表明,核极限学习机和BPNN 模型泛化能力较低,GA-KELM 和CNN 更具泛化性。造成这一现象的原因是：核极限学习机和BPNN 受模型初始权值随机性的影响,网络训练结果易陷入局部最优。本文提出的GA-KELM 模型能通过遗传算法实现模型输入权值的全局寻优,CNN 则能对大数据样本进行深度学习,因此2 种模型的泛化能力更强。

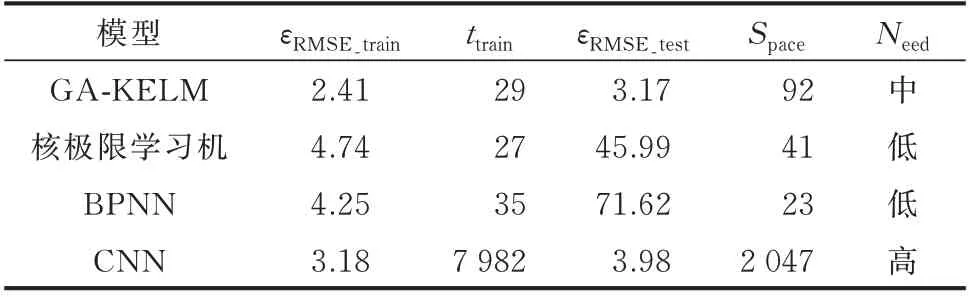
表1 模型指标对比Table 1 Comparison of model indices

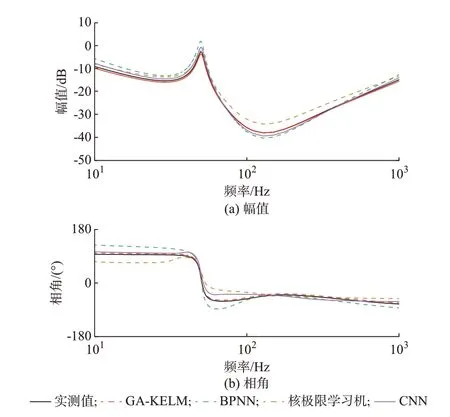
图5 采用不同模型获取的dq 阻抗测试结果Fig.5 Testing results of dq impedance acquired by different models

最后,对比各模型的训练平均时间ttrain、算法程序文件所占存储空间Space、模型对大数据的依赖程度Need。从表1 可以看出,CNN 模型训练耗时显著较长,其程序文件占用空间显著较大,对大数据的依赖程度也较高。这是由于CNN 学习过程复杂、训练迭代周期长导致的。GA-KELM 和核极限学习机的训练时间小于BPNN,远小于CNN。这一现象得益于核极限学习机仅包含单隐含层,网络架构和递推迭代过程较CNN 和BPNN 更为简单高效,因此训练用时较短。从表1 还可以看出,GA-KELM 模型训练时间、程序所占空间以及对大数据的依赖程度都要略逊于核极限学习机。这是由于GA-KELM模型需要采用遗传算法确定最优权值导致的。虽然各项指标有所增加,但模型泛化性得到了保证。

为实现并网逆变器多工况dq 阻抗的准确、及时获取,保障后续谐波稳定性分析结论的正确性和实用性,综合分析上述4 种模型的各指标对比结果后可以发现,本文选用的GA-KELM 模型具有阻抗获取精度高、泛化能力强、训练时间短的优势。