数学分析中一类与存在性有关的错误解法原因剖析
2022-03-21江樵芬
江樵芬, 徐 起
(福建师范大学 数学与信息学院, 福州350117)
1 引 言
数学类课程的学,学生除了在课堂上接受新知识之外,还有一个重要的环节——通过作业向教师反馈自己的掌握情况;而数学类课程的教,教师除了在课堂上讲授新知识之外,同样也有一个重要的环节——通过作业了解学生的掌握情况.数学类作业中出现的错误解答,远比正确解答更能反馈信息.特别是数学分析作业,由于课程特点,许多习题常有似是而非的解答,存在许多隐蔽性较强的错误.在数学分析作业中,常有学生最终答案是对的,但中间过程却是错误的;在数学分析课程考试后,也常有学生对答案时一脸喜色,成绩出来之后却觉得不可置信.这类隐蔽性较强的错误应该是学生学习的痛点,如何帮助学生理清这些痛点,这值得付出努力.
“存在性”在数学分析中几乎无处不在.与此同时,与“存在性”有关的作业解答中也存在较多隐蔽性错误.在一些与“存在性”有关的错误命题中,学生经常在存在反例说明命题不成立的情况下,仍觉得自己的证明没有错.这类隐蔽性错误不仅在学生的作业解答中频繁出现,而且在正式出版的专业书籍和正式发表的期刊论文中也偶尔有之,可见其迷惑性之大.
本文搜集了学生作业解答及正式出版物中与“存在性”有关的一些错误,也列举了学生在学习与“存在性”有关的命题时存在的一些困惑,按“忽略极限定义中δ对ε的依赖”“忽略介值与中值定理中介值点与中值点对其它因素的依赖”“二元函数中的存在性问题与一致性”等三个方面对这些错误及困惑进行分类,深入剖析其错误与困惑的原因,并给出了一些对策与教学建议.
2 若干概念或问题产生错误的原因分析
2.1 忽略极限定义中δ对ε的依赖而导致的错误
在数列极限、函数极限、连续性、一致连续性等极限相关概念中,都有“任给ε>0,存在N(δ,M)”等的叙述,我们知道这些存在的N,δ,M都依赖于ε,但一般教材的定义中较少用让学生能一眼看出的记号来体现这种依赖关系,尽管在定义之后会有这种依赖性的说明.学生形式地记住定义之后,做相应作业时常因忽略这种依赖性,只从文字叙述表面地看,从而导致了各种错误.通过[1]中的一个错误结论、[2]中的一个错误证明及学生作业中的一个错误证明来演示此类错误.
在[1]中有如下关于在x0连续与在x0的邻域内连续的错误结论.
例1[1](错误结论)设f(x)在x0连续且f(x0)≠0,则必存在x0的某个邻域,使f(x)在此邻域内连续.
错误证明[1]因为f(x)在x0连续,即∀ε>0,∃δ>0,∀x∈U(x0,δ)⟹|f(x)-f(x0)|<ε.今∀x′∈U(x0,δ),显然有|f(x′)-f(x0)|<ε.
又因为f(x0)≠0,当δ充分小时,由局部保号性知f(x′)f(x0)>0,从而f(x′)≠0.因而
|f(x)-f(x′)|≤|f(x)-f(x0)|+|f(x′)-f(x0)|<2ε.
所以f(x)在x′连续,由x′的任意性知f(x)在U(x0,δ)内连续.
容易举出反例说明例1的结论不成立.如令f(x)=xD(x)+1,其中D(x)是Dirichlet函数.易知f(x)在x0=0连续,f(0)=1,但f(x)在x0≠0间断.而细究[1]所给的证明,作者认为他找到了x0的δ邻域U(x0,δ),∀x′∈U(x0,δ),对∀x∈U(x0,δ)有|f(x)-f(x′)|<2ε,则f(x)在x′连续,从而f(x)在U(x0,δ)连续.但注意到上述的δ依赖于给定的ε,不妨记为δε.由给定的ε确定了δε之后,对U(x0,δε)中的x与x′成立的不等式|f(x)-f(x′)|<2ε中的ε,只能是确定δε的这个ε,不具任意性,故得不到f(x)在x′的连续性.该证明错误的根本原因在于忽略了函数在x0连续的定义中δ对ε的依赖性.
在[2]中有如下关于一致连续性的错误证明.


又f(x)在[a,+∞)上连续,从而可得f(x)在[a,M]上一致连续. 对∀x′,x″∈[M,+∞),有
|f(x′)-A|<ε, |f(x″)-A|<ε.
从而有
|f(x′)-f(x″)|=|f(x′)-A+A-f(x″)|≤|f(x′)-A|+|f(x″)-A|<2ε.
所以f(x)在[M,+∞)上一致连续. 则f(x)在[a,+∞)上一致连续.
与例1类似,例2证明错误的原因在于忽略了函数极限定义中M对ε的依赖性.证明中存在的M依赖于ε,不妨记为Mε.由给定的ε确定了Mε之后,对[Mε,+∞)中的任意两点x′,x″成立的不等式|f(x′)-f(x″)|<2ε中的ε只能是确定Mε的这个ε,不具任意性,故得不到f(x)在[M,+∞)的一致连续性.
这是一个十分典型的隐蔽性错误,不仅初学者难以辨别,解题经验丰富者也可能踩入此似是而非的陷阱,笔者也曾在某专注于数学考研的公众号上看到例2的这种错误证明.
作为数学分析的经典习题,例2的正确证明在较多的数学分析参考书中也可见.为了便于读者比较正确证明与错误证明的不同之处,加深对此类错误的理解,也列出例2的正确证明.下文几个证明错误但结论正确的例子也同样处理.

|f(x′)-f(x″)|≤|f(x′)-A|+|f(x″)-A|<ε.
又由f(x)在[a,+∞)上连续知f(x)在[a,Xε+1]上连续.由Cantor定理可知f(x)在[a,Xε+1]上一致连续.从而对上述ε>0,∃δ1>0,对∀x′,x″∈[a,Xε+1],|x′-x″|<δ1有
|f(x′)-f(x″)|<ε.
取δ=min{δ1,1}>0,对∀x′,x″∈[a,+∞),x′
由定义知f(x)在[a,+∞)一致连续.
无独有偶,在利用有限覆盖定理证明Cantor定理的作业中,也有部分学生出现此类错误.
例3利用有限覆盖定理证明Cantor定理.
错误证明∀ε>0,由f(x)在[a,b]连续知∀x0∈[a,b],∃δ0>0,当x∈U(x0,δ0)时,有
故对∀x′,x″∈U(x0,δ0)有
|f(x′)-f(x″)|≤|f(x′)-f(x0)|+|f(x0)-f(x″)|<ε.
从而f(x)在U(x0,δ0)上一致连续.
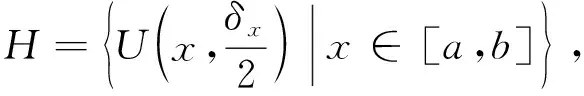


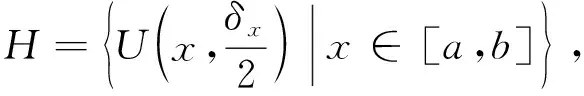
覆盖了 [a,b].
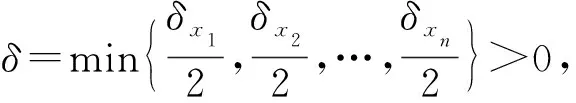
则
由定义知f(x)在[a,b]上一致连续.
对策:对于此类错误,建议将极限、连续定义中存在的N,δ,M等分别记为Nε,δε,Mε等,以直观地体现这种依赖性.[3]中也对极限定义的教学做了一些有益的探讨,有助于避免此类错误.
2.2 忽略介值与中值定理中介值点与中值点对其它因素的依赖导致的错误
各种介值、中值定理中存在的介值点与中值点通常既依赖于所讨论函数,也依赖于所讨论的区间端点.在解相关题目时,学生常忽略介值点、中值点对其它因素的依赖,由此导致了一些错误与困惑.分别以导数极限定理与洛必达法则逆命题不成立的困惑、一道积分极限题的错解为例来演示此类错误.
利用Lagrange中值定理易证导数极限定理,一般讲完该定理后会给出反例说明其逆命题不成立.但仍有学生在承认反例存在的情况下,找不出自己给出的证明的错误之处,并对这种矛盾现象感到困惑.
下面列出学生的错误结论及错误证明并分析其错误的原因.
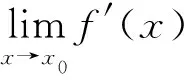


(*)
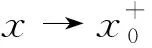
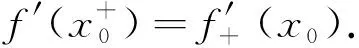
令
则
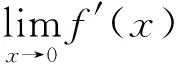
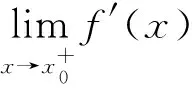
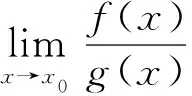
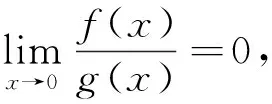
看看他的证明:

这种困惑也不是学生独有,[4]也存在类似的错误证明及由此得到的错误结论.
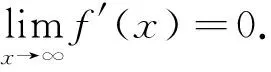
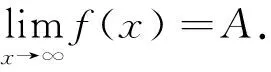

两边同时取x→∞时的极限,由于此时ξ→∞及
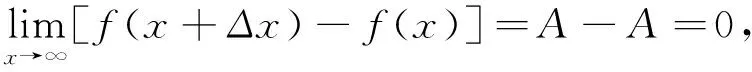
因此
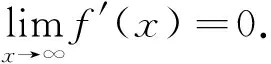
这个证明的错误之处与导数极限定理及洛必达法则之逆命题的错误证明一模一样.事实上,也容易举出反例说明该命题的必要性不成立.如令
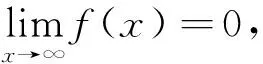
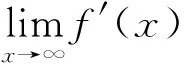
积分中值定理的应用中也常存在类似的错误.
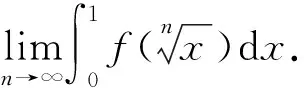
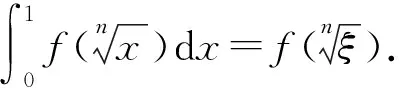
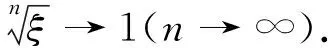
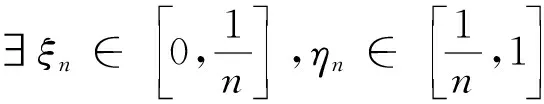
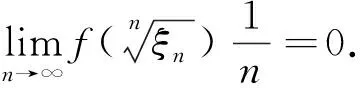

对策:对此类与介值、中值点有关的问题,若涉及到多个函数或区间端点在变动,在应用介值定理或中值定理时,存在的介值点或中值点不妨记为ξf或ξx,其中f,x分别为所涉及的函数与端点.
2.3 二元函数中的存在性问题与一致性
在研究二元函数时,常固定一个变量,把二元函数视为关于另一个变量的一元函数,利用这些一元函数的性质研究二元函数的对应性质,如考虑二元函数的偏导数、二元函数对某个分量的连续性等,这是处理二元函数的常见思路.但要注意到二元函数把一个变量固定之后得到的一元函数,一般与所固定的那个变量的值有关,所固定变量的不同取值对应不同的一元函数.忽略这种相关性容易导致一些本质性错误.讨论此类一元函数的极限或连续性时,在ε-δ(N,M)定义中对任意ε>0存在的δ(N,M),不仅依赖于ε,还依赖于所固定的变量.学生常忽略δ(N,M)对所固定变量的依赖性,较肤浅表面地应用ε-δ(N,M)定义证明得到一些错误结论.
下面以函数列极限函数的连续性、二元函数对x及对y的连续性与二元函数连续性的关系为例来演示此类错误.
在讨论函数列极限函数的连续性时,一般会给出反例说明函数列点点收敛不足以保证极限函数的连续性,但仍有同学在承认反例存在的情况下,对“点点收敛的连续函数列,其极限函数也连续”这个错误结论给出如下自认为没问题的证明.
例7(错误结论)设{fn(x)}在I上点点收敛到f(x),若fn(x)在I上连续,则f(x)在I上也连续.
错误证明∀x0∈I,∀ε>0,{fn(x)}在I点点收敛到f(x),故对∀x∈I,∃N∈,对∀n>N有特别地有又由fN+1(x)在x0连续可知∃δ>0,对∀x∈I且|x-x0|<δ,有因此
由定义知f(x)在x0连续.由x0的任意性知f(x)在I上连续.
令fn(x)=xn,x∈[0,1],易知fn(x)在[0,1]上连续,且fn(x)在[0,1]上点点收敛到
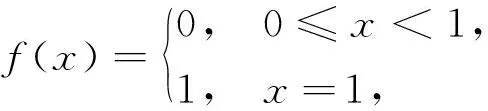
而f(x)在x=1不连续.这个反例说明了例7的结论是错误的.
这个证明错误的原因在于忽略了函数列点点收敛的极限定义中,存在的正整数N不仅依赖于ε,还依赖于x,不妨记为Nx.由此在插项时对不同的x所插的项fNx+1(x)未必相同,从而不能由某个固定的fN+1(x)在x0的连续性得到所要找的δ.为了找到这样的δ,期望能找到一个公共的N对I中所有的x都适用,这便是{fn(x)}在I上的一致收敛性.
N依赖于ε,x,这还是比较粗浅的理解,这个问题更根本的原因在于当{fn(x)}在I上点点收敛时,对于无穷多个x∈I,对应的可能有无穷多个Nx,对这无穷多个正整数取上确界可能会取到+∞.因此不一定能找到那个想要的、适合拿来插项的N.若这无穷多个Nx存在有限的上确界,那便是{fn(x)}在I上一致收敛.深入理解这个证明的错误之处,有助于理解函数列极限函数连续性定理的条件中为何要有一致收敛性.
[5]中课后习题利用对x与对y的连续性给出了二元函数连续的一个充分条件,学生在证明时也常犯与例7一样的错误.
例8[5]设f(x,y)定义在闭矩形域S=[a,b]×[c,d]上.若f对y在[c,d]上处处连续,对x在[a,b]上(且关于y)为一致连续,则f在S上处处连续.
错误证明∀(x0,y0)∈[a,b]×[c,d],∀ε>0,f(x,y)对y在[c,d]连续,则f(x0,y)在y0连续,则∃δ1>0,∀y∈[c,d]且|y-y0|<δ1有
f(x,y)对x在[a,b]连续,则f(x,y)在x0连续,则∃δ2>0,∀x∈[a,b]且|x-x0|<δ2有
令δ=min{δ1,δ2},对∀(x,y)∈S,|x-x0|<δ且|y-y0|<δ有
由定义知f(x,y)作为二元函数在(x0,y0)连续.由(x0,y0)的任意性知f(x,y)在S连续.
学生的这种证法只用到了对x与对y的连续性,并没有用到“对x的连续性关于y一致”这个条件.而只有对x与对y的连续性不足以得到f在S上的连续性.这也容易找到反例.如令

细究其证明可以发现,f(x,y)作为x的一元函数与y有关,不同的y对应不同的一元函数f(x,y),从而存在的δ2不仅依赖于ε,也依赖于y,不妨记为δy.由此取的δ=min{δ1,δy}与y有关,这不是二元函数连续定义中合适的δ,证明到此过不去.
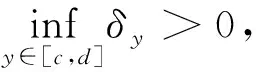
[6]中也对这个结论的此类错误证明进行分析.但作者认为“一致连续”有两层含义,除了如我们上面所分析的一样,“一致连续”的意思指的是存在的δ与y无关之外,还有另一层含义是指对每个固定的y,把f(x,y)当成x的一元函数是一致连续的.这种理解是错误的,从我们的分析很容易看出题中条件“一致连续”并无[6]所认为的这层意思.
正确证明∀(x0,y0)∈[a,b]×[c,d],∀ε>0,f(x,y)在(x0,y0)对y连续,也即f(x0,y)在y0连续,故∃δ1>0,对∀y∈[c,d],当|y-y0|<δ1时有|f(x0,y)-f(x0,y0)|<ε.
f(x,y)对x在[a,b]上关于y为一致连续,则对上述∀ε>0,∃δ2>0,对∀y∈[c,d],∀x∈[a,b],当|x-x0|<δ2时,有|f(x,y)-f(x0,y)|<ε.
令δ=min{δ1,δ2}>0,对∀(x,y)∈[a,b]×[c,d],|x-x0|<δ且|y-y0|<δ有
|f(x,y)-f(x0,y0)|≤|f(x,y)-f(x0,y)|+|f(x0,y)-f(x0,y0)|<ε+ε=2ε.
由定义知f(x,y)在(x0,y0)连续.由(x0,y0)的任意性知f(x,y)在[a,b]×[c,d]连续.
对策:对于此类错误,建议在教学中强调f(x,y)视为关于变量x(y)的一元函数时,与另一变量y(x)的关系,并把在ε-δ定义中存在的δ记为δy(δx)以体现依赖性.
3 进一步的教学尝试
为解决学生在学习过程中反馈出来的错误与困惑之处,在教学实践中还做过如下尝试:在每一章设计相关的判断题,让学生对正确的结论给出证明,错误的结论给出反例,以此锻炼学生的思辨能力;对较隐蔽的错误解法分类整理,在对应章节布置找茬题;把一些难度适中的错误命题做成开放性的讨论题,鼓励学生观察发现证明过不去的地方,思考如何补充条件来改进.这些尝试也为培养学生良好的数学学习习惯起了一定作用.
4 结 论
“存在性”在数学分析中几乎无处不在,而学生在解决与存在性有关的问题时也时常犯各种错误,且这些错误的隐蔽性通常比较强.本文深入剖析了这些错误的原因,并按错误原因进行分类,同时给出了一些教学上的对策与建议以期减少学生学习过程中的此类错误.从近年来本校学生的作业反馈中可以发现,本文的错误原因分析及各种教学尝试对解决此类隐蔽性错误是非常有效的.
致谢本文的一些想法曾在2020年8月复旦大学主办、大连理工大学与扬州大学协办的数学分析教学研讨会上做过交流,作者感谢楼红卫教授的邀请,感谢与会专家提出的宝贵意见.作者也感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.
