基于希尔伯特-黄变换的汽车耐久性载荷谱编辑

晋 杰，张佳云，周 炜，徐中明，张 禄

(1. 交通运输部公路科学研究院，北京 100088;2. 重庆大学机械与运载工程学院，重庆 400044)

0 引言

随着汽车产业竞争日益激烈，为缩短产品开发周期、降低成本，耐久性快速评价技术已成为国内外车企进行产品验证的主要手段。目前耐久性试验有用户实际道路试验、试验场道路试验和室内道路模拟试验3类。室内道路模拟试验可免去场地租赁、驾驶员聘用等问题，并可对试验载荷谱加以编辑来提高效率，缩短试验时间，因此应用广泛[1]，其中的虚拟迭代技术很好地建立了试验与仿真结果之间的联系[2]。室内模拟试验不仅应实现试验时间的大幅缩短，还当完好复现车辆运行状态，故载荷谱的制定尤为重要，将影响到试验效率及结果准确性。室内道路模拟试验通常有两种载荷谱加载方式：一类是程序谱加载[3]；另一类则是实测道路载荷谱加载[1]。对于实测道路载荷谱加载而言，为了加速耐久性试验，采取合理有效的载荷谱编制方法对实测载荷谱进行加速处理是十分重要的一步。

目前载荷谱编制方法多样，基本原理都是删除信号里损伤贡献量小的循环以缩短加载时间[4-11]。各方法之间的差异主要表现在损伤量识别及删除的方式上，可通过设定损伤、应变、载荷谱等指标的阈值来剔除无效信号，实现载荷谱的加速。郑松林等[4]提出基于各路段最小标准差谱组合的载荷谱加速方法，把阈值设定为零部件的对称弯曲疲劳极限的0.65倍，删除低幅值载荷时间历程，最终将载荷谱压缩为原载荷谱时长的45%，加速效果较为明显。朱连峰等[5]通过对试验场各类典型工况载荷谱设置损伤阈值，并考虑载荷特征变化和相对变化速率之间关系进行编制，最终节省了近48%的试验时间。STEPHENS 等[6]使用应变幅值与SWT参数编辑两种技术编制了某变幅应变信号，通过设定信号阈值，保留高于阈值的循环，均实现了编辑加速的效果。董国疆等[7]通过以试验场实测轮心六分力信号为对象，从多个角度对比了伪损伤保留法、损伤保留法和峰谷值抽取法3种方法的优劣，得出损伤保留法更具优势的结论。葛文韬等[8]提出了一种可以完整保留长里程路面载荷谱损伤值、幅值特性以及频率特性的编制方法，通过时域信号编辑将比利时路单次循环路面里程数减少了约42.9%。

信号的损伤量一般与幅值成正比例关系[9]，可通过信号分析识别出幅值较大片段，进而确定损伤贡献较大片段。上官文斌等[9]提出基于小波变换的汽车零部件加速耐久性载荷谱编辑方法，利用包络线损伤识别法，来识别并提取损伤贡献大的片段，以汽车动力总成悬置的载荷谱为例，利用该方法实现将载荷谱压缩至原始载荷谱的77.89%。短时傅里叶变换也可以应用于汽车零部件载荷信号编辑[10]，利用累积功率谱密度来识别并提取损伤贡献大的片段，将载荷谱压缩至原始载荷谱的75.42%。针对小波变换与短时傅里叶变换存在的不足，董国疆等[11]提出了基于S变换理论的汽车零部件疲劳载荷谱编辑方法，利用S变换获取载荷信号的时频幅值谱并以此来识别损伤贡献小的载荷片段，利用该方法可将载荷谱压缩至原始载荷谱的53.35%。由于试验场载荷谱通常呈现很强的特征性，大载荷与小载荷有较明显的区分，为进一步验证编辑方法的有效性，本研究以某实际用户道路采集的载荷谱作为处理对象。对于用户道路载荷谱，由于车速、工况以及道路状况等的变化使得载荷信号通常具有非平稳特征，即载荷信号在时域上不存在规律性，而希尔伯特-黄变换(HHT)则是一种能够有效分析非平稳信号的信号时频分析方法，广泛应用于结构损伤侦测、故障检测等领域。N.Roveri等[12]提出了一种基于希尔伯特-黄变换的桥梁结构在移动载荷作用下的损伤检测方法，通过对第一瞬时频率的直接检测，准确检测出了损伤的存在和位置。希尔伯特-黄变换也可与卷积神经网络等相结合，在单一与复合工况下使端到端的轴承故障检测正确率提升到100% 和99.74%[13]。希尔伯特-黄变换[14]可以将任何复杂信号分解成固有模态函数的叠加，再对各固有模态函数作Hilbert变换，获得信号“时间-频率-振幅”的三维谱分布。

对于汽车耐久试验中的载荷信号，利用希尔伯特-黄变换方法进行时频分析，获取瞬时能量谱并以此为据识别并提取信号中损伤贡献量大的片段，以实现载荷谱的加速。针对汽车耐久性载荷谱加速需求，提出一种基于希尔伯特-黄变换的载荷谱编辑方法，在实现伪损伤等效的基础上，同时满足压缩信号在统计参数(均方根、峰度系数)、能量及信号的幅值分布等方面均与原始信号有较好的吻合。以某型汽车用户道路实测车轮六分力载荷信号为例，分别采用希尔伯特-黄变换和损伤保留编辑方法进行编辑压缩，获得压缩载荷信号，从统计参数和信号幅值分布等方面对编辑前后的载荷信号进行对比，验证提出的基于希尔伯特-黄变换载荷编辑方法的有效性与优越性。

1 载荷信号采集与信号特征参数

1.1 汽车耐久性载荷谱采集

对某工程自卸车用户道路的车轮六分力载荷谱进行采集，测试车辆空载质量为15 t，满载质量为31 t，前后共4轴，轴距分别为1 800+2 500+1 350 mm，前轮距2 048 mm，后轮距1 860 mm。测试用六分力传感器为美国某科技公司生产的MSCLW-2T-100K-S型，采样频率设置500 Hz。实车装配如图1(a) 所示；试验数采系统为SoMat eDAQ，如图1(b) 所示；实车采集的用户道路情况如图1(c) 所示。实车测试传感器安装采用交叉轴的安装方式，如图2所示，深色部分表示安装六分力传感器的车轮。

图1 载荷谱采集过程Fig.1 Load spectrum acquisition process

图2 六分力传感器安装位置示意图Fig.2 Schematic diagram of installation positions of six-component force sensor

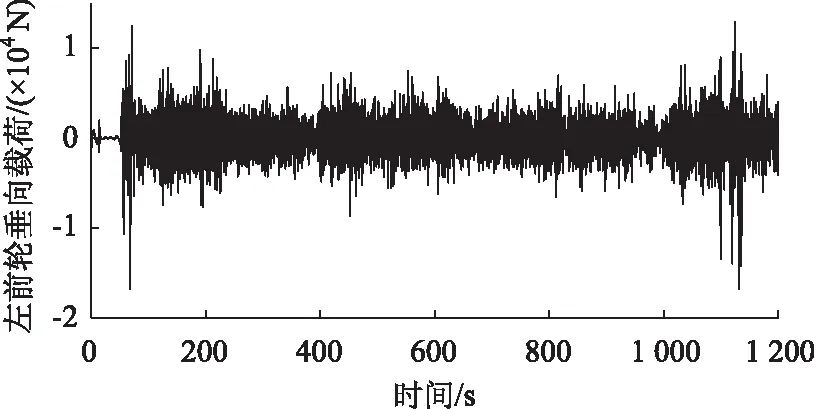
图3 左前轮垂向载荷信号Fig.3 Vertical load signal of left front wheel

试验采集的载荷信号通常存在干扰、失真等现象，会对结果造成影响。因此进行信号编辑之前，先进行信号的预处理。首先，通过设置0.1 Hz的高通滤波器实现漂移修正，再使用手动选择去除信号中的毛刺部分，而一般路面激励小于50 Hz，设置重采样频率为100 Hz，进行重采样处理。图3为预处理后的左前轮垂向载荷信号FZ(t)，信号总时间长度为1 200 s。

1.2 载荷信号特征参数

对于载荷信号，可从损伤值、统计特征参数、功率谱及穿级计数等方面描述其特征，以评价载荷信号的编辑效果。

(1)伪损伤值

利用标准S-N曲线和Miner线性损伤累计准则，不做平均应力修正，计算各应力循环的损伤值，累计求和后就是载荷信号的伪损伤值。伪损伤计算式为：

(1)

式中，ni为某一应力水平下的循环次数；Ni为该应力水平下循环到破坏的次数。

伪损伤的绝对数值并无太多实质意义，通常关注的是伪损伤值之间的比例关系。

(2)统计参数

均方根为统计2阶矩，能够衡量随机信号所含的平均功率，均方根值越小，载荷信号平均能量越小；峰度系数为统计4阶矩，是表征概率密度分布曲线在平均值处峰值高低的特征数[15]。载荷信号的均值对零件的疲劳寿命有明显的影响。

均值μ、均方根值RMS和峰度系数k计算式分别为：

(2)

(3)

(4)

式中，FZ(ti)为载荷信号；FZ(t)为对应ti时刻的幅值；σ为FZ(t)的标准差；E为期望值。

(3)功率谱密度

功率谱密度P描述信号功率在频域内的分布情况。

(5)

式中，T为截断时间;FZ(f)为载荷信号FZ(t)的傅里叶变换。

(4)穿级计数

穿级计数是一种单参数计数法，将整个载荷幅值范围分成等间距的若干级，如图4(a)所示；并统计信号采样点上升或下降时穿过某一级的次数，能反映信号在各载荷水平的分布情况，如图4(b)所示。

图4 穿级技数法原理Fig.4 Principle of level cross counting

2 希尔伯特-黄变换与信号编辑方法

2.1 希尔伯特-黄变换原理

希尔伯特-黄变换(HHT)是Huang等[14]于1998年提出的一种自适应信号分析方法，包括经验模态分解和Hilbert变换。HHT假设任一复杂信号都是由若干固有模态函数(IMF)组成，经验模态分解能把信号分解为若干固有模态函数。对每个固有模态函数作Hilbert变换，可获得信号“时间-频率-振幅”的三维谱分布，以分析信号的时频特性。固有模态函数应满足条件：

(1)在整个数据长度，极值和过0点的数目应相等或至多相差1个。

(2)在任意时刻，由局部极大值和极小值点分别确定的上下包络线的均值为0。

2.1.1 经验模态分解

经验模态分解算法具体步骤为：

(1)对某载荷信号x(t)，确定x(t)的所有极值点，用3次样条曲线连接所有极大值点形成上包络线xmax(t)，同样方法形成下包络线xmin(t)。计算上下包络线均值：

m1(t)=[xmax(t)+xmin(t)]/2。

(6)

(2)记x(t)与m1(t)的差为h1(t)，则有：

h1(t)=x(t)-m1(t)。

(7)

(3)将h1(t)视作原信号，重复上述(1),(2)步骤，即得：

h11(t)=h1(t)-m11(t)，

(8)

式中m11(t)是h1(t)的上、下包络线均值。

第k次筛选的数据h1k(t)可表示为：

h1k(t)=h1(k-1)(t)-m1k(t)。

(9)

当h1k(t)满足终止准则时，终止迭代，并将其视为第1阶固有模态函数，记为IMF1(t)，即

IMF1(t)=h1k(t)。

(10)

若严格以固有模态函数定义作为迭代的终止准则，可能会导致固有模态函数没有物理意义[16]，终止准则可采用柯西类型判据，即由两个连续的处理结果h1(k-1)(t)与h1k(t)之间的相对公差SD来确定，定义为：

(11)

根据试验结果，Huang提出SD的最佳取值范围为0.2～0.3之间。本研究SD值取0.2，即当SD≤0.2时，迭代终止。

(4)得到第1阶IMF后，包含较低阶频率成分的残余信号r1(t)为：

r1(t)=x(t)-IMF1(t)。

(12)

把r1(t)作为新信号，重复上述(1)、(2)、(3)步骤，依次得到：

(13)

式中，IMFi(t)为第i阶IMF；rn(t)为残余项。

当残余分量rn(t)为单调函数时，结束整个经验模态分解过程。

(5)原始信号x(t)便被分解为若干固有模态函数IMFi(t)，i=1,2,…,n以及一个残差函数rn(t)的线性叠加，即：

(14)

2.1.2 Hilbert变换

对上述每阶IMF分量作Hilbert变换，有：

(15)

式中PV代表柯西主值。

于是构造解析信号Zi(t)：

Zi(t)=IMFi(t)+jH[IMFi(t)]=ai(t)ejθi(t)。

(16)

其中幅值函数ai(t)、相位函数θi(t)分别为

(17)

(18)

瞬时频率被定义为：

(19)

则信号x(t)表示为：

(20)

式中Re取实部。

由式(19)，可将信号的瞬时频率、振幅和时间表示在同一个三维图中，这种振幅在频率-时间平面上的分布定义为Hilbert谱图，记为H(ω,t)。

则进一步有：

(21)

IE(t)即为信号x(t)的瞬时能量随时间的分布函数。

信号边际谱h(ω)为信号累积振幅随频率分布情况，计算式为：

(22)

2.2 基于希尔伯特-黄变换的载荷信号编辑方法

对于载荷信号，可利用HHT获得信号的瞬时能量谱，瞬时能量越大表明对结构损伤贡献越大。通过对瞬时能量设定阈值，找到低于阈值的瞬时能量谱时间轴，删除相应原信号时间片段，并对余下信号片段拼接组合，即可获得缩减信号。

以试验车左前轮垂向载荷信号FZ(t)为例，基于HHT的信号编辑流程如图5所示，具体步骤如下。

图5 基于HHT的载荷谱编辑流程Fig.5 Editing process of load spectrum based on HHT

(1)载荷信号的输入。输入经预处理后的左前轮垂向载荷信号FZ(t)。

(2)载荷信号的希尔伯特-黄变换。对FZ(t)进行经验模态分解，获得若干固有模态函数，如图6所示。对各固有模态函数作Hilbert变换，获取信号的希尔伯特谱，如图7所示，表示信号能量在时频域的分布情况；其瞬时能量谱如图8所示，表征了信号能量在时域的分布情况，可见载荷信号具有典型的非平稳特征。

图6 固有模态函数Fig.6 Intrinsic mode function

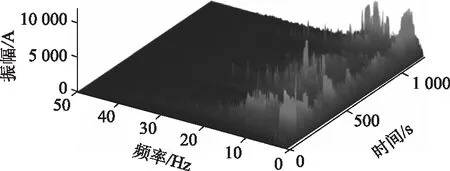
图7 Hilbert谱Fig.7 Hilbert spectrum

图8 左前轮垂向载荷瞬时能量谱Fig.8 Instantaneous energy spectrum of vertical load of left front wheel

(3)基于遗传算法的瞬时能量谱阈值最优化。

由于无法主观地确定阈值的大小，为实现压缩效果的最优，通过遗传算法对阈值进行寻优。以瞬时能量谱阈值y为设计变量，以载荷信号编辑前后的信号压缩比c(y)最小为目标函数，以压缩载荷信号与原始载荷信号的损伤之比(损伤保留量)D(FZy(t))≥0.93为约束条件，利用遗传算法，得到给定区间[0,maxIE(t)]内的最优阈值。记原始载荷信号为FZ0(t)，时间长度L0，压缩后信号为FZy(t)，时间长度Ly。阈值的优化数学模型可以表达为：

(23)

基于阈值优化数学模型，采取遗传算法寻优，计算得到用户道路载荷信号FZ(t)瞬时能量谱的最佳阈值为2.099×106，目标函数信号压缩比c(y)的最小值为0.76，损伤贡献保留量D[FZy(t)]为0.93。

(4)识别并提取损伤贡献大的信号片段，完成信号缩减。将瞬时能量谱中小于最佳阈值的时间片段识别出来，如图9(a) 中阴影区域。并对应于原始载荷信号中，将原始载荷信号相同位置的时间片段删除，如图9(b) 中阴影区域。将剩余时间片段通过正弦信号组合的方式拼接获得总压缩信号。

图9 基于HHT的载荷谱编辑方法Fig.9 HHT based load spectrum editing method

3 载荷谱编辑结果分析

为检验基于HHT的载荷谱编辑方法效果，选择基于损伤保留的编辑方法对比分析。对汽车左前轮垂向载荷信号FZ(t)，在nCode中采用基于损伤保留的方法进行编辑。

基于损伤保留编辑方法的原理为，先对原始载荷信号的时间轴等距离分割处理，计算各时间段的损伤值；再基于设定的损伤保留量，删除小损伤量的信号片段，实现指定损伤保留量下信号的缩减[17]。

对左前轮垂向载荷信号FZ(t)，设置损伤保留量为93%，窗长为1.5 s。时域信号损伤时间分布如图10(a)所示，将小损伤量信号片段识别出来见图10(a)中阴影区域，并将原始载荷信号中相同位置的时间片段删除，见图10(b) 中阴影区域。将剩余的时间片段通过正弦信号组合的方式拼接获得总压缩信号。

图10 基于损伤保留的载荷谱编辑方法Fig.10 Damage retention based load spectrum editing method

3.1 压缩比分析

分别记基于HHT变换编辑所得加速信号为压缩载荷Ⅰ，基于损伤保留编辑所得加速信号为压缩载荷Ⅱ，原始信号及两种方法所得压缩信号依次如图11所示。原始载荷信号总长为1 200 s，基于HHT的编辑方法将信号长度缩减到913 s，压缩至原始载荷信号的76%；基于损伤保留的编辑方法将信号长度缩减到960 s，压缩至原始载荷信号的80%。

图11 压缩比分析Fig.11 Compression ratio analysis

为防止压缩载荷信号与原始载荷信号的特征存在较大差异，对压缩载荷信号和原始载荷信号从功率谱密度、统计参数及穿级计数等方面进行分析对比。

3.2 功率谱密度分析

分析对比编辑前后信号的功率谱密度，需满足信号在频域特性的一致性。以往文献中[18]，更多是从时域损伤角度来检验编辑方法的有效性。然而动态载荷作用下，共振频率附近结构的响应大幅提高，造成载荷急剧增加，会对疲劳寿命产生较大影响。因此，还应从频域特性方面来检验该编辑方法的可行性。

通过其功率谱密度的对比，可分析载荷信号在编辑前后功率如何随频率分布的变化情况。采用线性平均方法，设置进行FFT的时长为10.24 s，即频率分辨率为0.098 Hz，数据重叠率为67%，求取各信号的功率谱密度。

原始信号与两种压缩信号的PSD如图12所示。对比分析可知，原始信号与压缩信号的频带为0.5～15 Hz。在各频率上两方法获取的压缩信号功率谱密度分布、变化趋势与原信号相同，说明两种方法均未改变载荷信号频域特性，证明两种编辑方法的有效性。

图12 编辑前后载荷信号功率谱密度Fig.12 Power spectral densities of load signal before/after editing

3.3 边际谱分析

通过分析载荷信号的边际谱，可以得到编辑前后载荷信号累积振幅(或能量)随频率分布的变化情况。如图13可知，两种编辑方法获取的缩减信号边际谱的分布、变化趋势与原始信号一致，两种方法无明显的区别，表明两种编辑方法删除的载荷片段有一定的相似性，表明两种编辑方法的有效性。

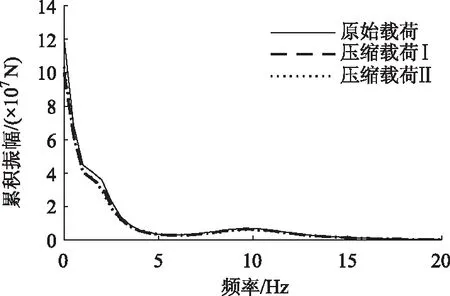
图13 编辑前后载荷信号边际谱Fig.13 Marginal spectra of load signal before/after editing

3.4 统计参数分析

基于HHT的编辑方法与基于损伤保留编辑方法获取的信号损伤保留量、统计参数(均方根、峰度系数和均值)及统计参数变化量，如表1所示。两种编制方法均保证压缩载荷损伤保留量为93%，满足信号编辑前后损伤的等效，压缩信号Ⅰ的压缩比为76%，压缩信号Ⅱ的压缩比为80%。即相较基于损伤保留编辑，基于HHT的编辑方法能在损伤保留一致的情况下，进一步压缩原始信号。

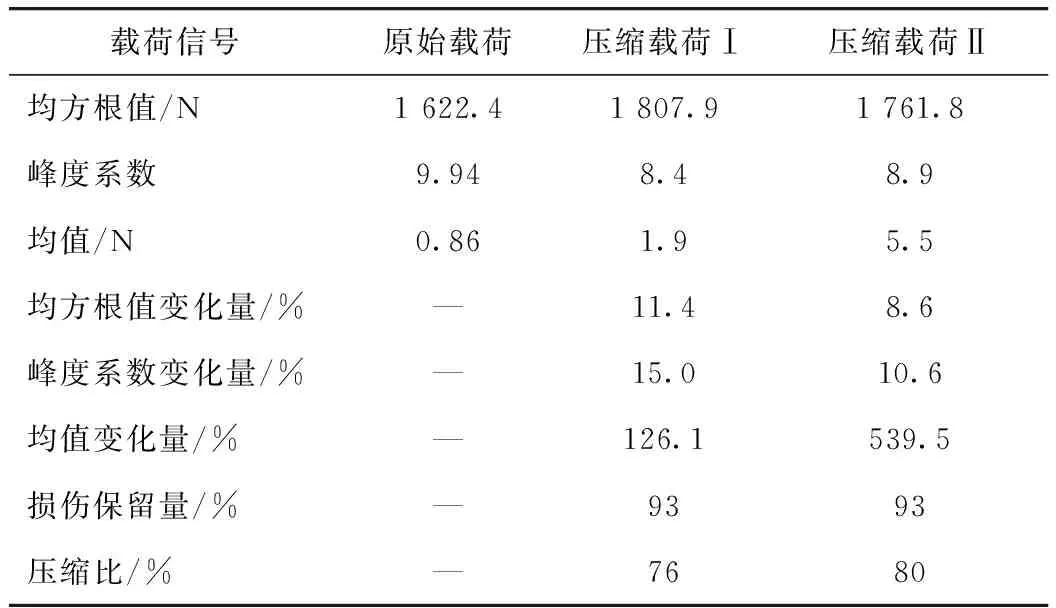
表1 两种编辑方法下压缩信号的统计参数及变化量Tab.1 Statistical parameters and variations of compressed signal by 2 editing methods

载荷信号的均值对零件疲劳寿命影响较大，压缩载荷Ⅰ的均值变化量为126.1%，远远小于压缩载荷Ⅱ的539.5%，更多地保留原始载荷的特性。此外，由于小幅值循环的删除，单位时间内能量变大，压缩载荷信号的均方根值增大。当均值附近的小幅值循环被删除后，小幅值出现的概率变小，因此压缩载荷信号峰度系数变小。由表1可见，两压缩载荷的均方值、峰度系数变化量基本一致，且均在15%以下，说明与原始信号吻合较好。

3.5 穿级计数分析

对原始载荷和压缩载荷Ⅰ，Ⅱ进行穿级计数，得到信号幅值与该幅值出现频次间的关系。

由图14可得，相比原始载荷信号，在小幅值循环频次上，基于HHT的压缩载荷Ⅰ和基于损伤保留的压缩载荷Ⅱ存在明显缩减，在大幅值循环频次上与原始信号相吻合。而小幅值载荷对信号损伤贡献一般很小，且在小幅值循环频次上，压缩载荷Ⅰ相比压缩载荷Ⅱ缩减得更多。综上，基于HHT的编辑方法压缩效果总体更优。

图14 编辑前后载荷信号穿级计数Fig.14 Level cross countings of load signal before/after editing

4 结论

针对用户道路实测汽车载荷谱，提出一种基于希尔伯特-黄变换的耐久性载荷编辑方法。基于信号瞬时能量与疲劳损伤贡献量之间的关系，利用希尔伯特-黄变换及遗传算法得到最优瞬时能量谱阈值，能将原始信号中损伤贡献大的信号片段识别提取出来。在保证损伤保留量均为93%的前提下，传统的基于损伤保留编辑方法可将原始载荷信号压缩至原时长的80%，而基于希尔伯特-黄变换编辑方法可将原始载荷信号压缩至原时长的76%，在小幅值载荷删除更多的同时未改变载荷信号频域特性。均方根值、峰度系数变化量两者基本保持一致，均在15%以下，且后者的均值变化量远远小于前者，表明希尔伯特-黄变换相比传统的基于损伤保留编辑方法效果更优，可用于汽车耐久性试验中载荷谱的编辑与加速。