粘贴双L形钢板加固PC简支T梁的抗剪性能
2022-03-21高华睿
叶 欣,高 磊,熊 文,高华睿
(1. 南京交通职业技术学院 路桥与港航工程学院,江苏 南京 211188;2.山东大学 岩土与结构工程研究中心,山东 济南 250061;3.东南大学 交通学院,江苏 南京 211189;4.山东高速建设管理集团有限公司,山东 济南 250002)
0 引言
粘贴钢板和FRP片材加固法[1-2]是提高已建混凝土结构构件承载力和改善使用性能的有效方法,而粘贴钢板的加固更具有良好的经济性,许多维修加固现场条件适合采用。
对粘贴钢板加固混凝土梁的研究,早期主要集中在钢筋混凝土梁、板的正截面抗弯加固的性能、破坏形式及钢板锚固机理等问题上,而后展开了对钢筋混凝土梁斜截面抗剪进行粘贴钢板加固的研究。钢筋混凝土梁本身的抗剪影响因素比较多,相互交织[3-4],尽管研究人员提出了诸如修正压缩场理论、Strut和Tie模型等分析模型来揭示了钢筋混凝土梁抗剪性能[5],但用于钢筋混凝土梁斜截面抗剪的粘贴钢板加固研究上更加复杂。因此,可行的研究方法是基于类似美国AASHTO规范[6]和ACI规范[7]等所限定的、简化模型计算方法,结合粘贴钢板加固混凝土试验梁的观测分析[4]进行。由此进行的粘贴钢板加固钢筋混凝土梁斜截面抗剪的受力性能、破坏形式、受剪承载力计算以及粘贴钢板布置构造等的系统研究,得到了不少有价值的成果[8-16]。
在已建的公路混凝土梁桥中,许多是采用后张法预应力混凝土T梁和小箱梁、整体截面的箱梁等,由于施工、超载车辆以及设计等原因,其中有一些预应力混凝土梁出现斜截面抗剪承载力不足,以及出现梁体斜裂缝宽度较大的现象[8],但是,已颁布的相关加固设计规范[17-18]只有对粘贴钢板加固钢筋混凝土受弯构件的计算方法和构造要求,并且目前对粘贴钢板加固后预应力混凝土梁的抗剪研究文献很少,因此,需要对粘贴钢板进行预应力混凝土梁抗剪加固后的斜截面破坏形态、原构件箍筋和粘贴钢板的受力行为等性能进行研究,进而研究加固设计计算方法。
对混凝土受弯构件的抗剪加固,已有研究[15,19]和加固设计规范[17-18]主推粘贴U形钢箍板,但其加工和粘贴施工难度较大。而双L形钢箍板是U形钢箍板的改进,两块加工成型的L形钢箍板分别粘贴到梁上,同时L形钢箍板下肢相互粘贴形成类U形钢箍板。L形钢箍板具有钢板加工和粘贴施工比较容易、涂建筑胶层容易控制、对构件局部尺寸微小变化适应性较强优点,但对其锚固和加固效果目前尚认识不足。
本研究通过粘贴双L形钢箍板加固预应力混凝土简支T梁的室内模型抗剪对比试验,结合空间有限元非线性分析来进一步研究加固后抗剪性能与有效性,并研究建议了粘贴钢箍板加固预应力混凝土梁的计算方法。
1 室内模型试验研究
对2片截面尺寸和配筋、制备材料与加载控制等均相同的预应力混凝土简支T形截面试验梁(1片为未加固梁,称参照梁;1片为加固梁)进行静载试验,观测研究存在损伤(梁体出现斜裂缝)且加载不移除条件下加固后的T形截面试验梁(模拟构件二次受力)破坏形态、箍筋与钢箍板的受力行为;与参照梁斜截面破坏试验比较,观测研究粘贴加固后对构件受力性能,即抗剪承载力、构件抗弯刚度等的影响。观察在加固梁受力全过程双L形钢箍板与梁之间的粘贴剥离现象。
1.1 试验梁概况
(1)试验梁设计
设计制作预应力混凝土简支T形截面试验梁2片:参照梁(编号PCT-0)和加固梁(编号PCT-1)各1片。试验梁设计混凝土强度等级均为C40,梁长L=2 600 mm,计算跨径L0=2 400 mm,梁截面尺寸均相同,见图1。后张法预应力混凝土试验梁直线布置1根7φs12.7低松弛预应力钢绞线,张拉控制应力σcon=1 395 MPa,锚具采用锥形锚,试验设计预应力度λ=0.35,为部分预应力混凝土简支T梁。箍筋布置间距为200 mm。

图1 试验梁设计与加载示意图(单位:mm)Fig.1 Schematic diagram of test beam design and loading (unit: mm)
抗剪加固梁PCT-1在梁两侧剪跨段垂直粘贴双L形钢板箍加固(见图2),钢板强度等级为Q345,厚度为2 mm,钢板箍宽度为30 mm。箍板长肢长度为312 mm,短肢长度为110 mm,两条L形钢箍板依次粘贴到梁上,同时L形钢箍板下肢相互粘贴形成类U形钢箍板。在L形钢箍板上端粘贴宽60 mm钢板压条,加固时,钢压条下涂抹粘胶加以填平,打入直径8 mm 的螺栓加以锚固。
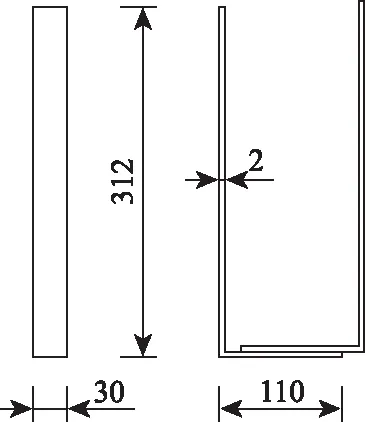
图2 双L形钢板箍(单位:mm)Fig.2 Double L-shaped steel plate (unit: mm)
(2)试验梁材料实测力学指标
参照规范[20]要求对试验梁制备混凝土试块力学性能指标进行实测,得到混凝土立方体实测抗压强度fcu=44.1 MPa,抗压弹性模量Ec=3.28×104MPa。
试验梁截面通长布置2根直径HRB335非预应力纵向钢筋,箍筋采用HPB300光圆钢筋,实测的力学性能指标见表1。

表1 钢材及钢筋实测力学性能指标Tab.1 Measured mechanical properties of steel bars
粘钢结构环氧树脂胶固化温度在25 ℃左右时,24 h撤出加压固定系统,72 h后可以投入使用,剪切强度40 MPa。
实测参照梁PCT-0和加固梁PCT-1加载前的钢绞线预应力分别为1 026 MPa和882 MPa。
(3)试验加载
试验梁两端各布置一个钢板铰支座,试验梁上放置分配梁(见图3)。剪跨段长0.6 m,剪跨比1.89。

图3 试验梁加载Fig.3 Test beam loading
参照梁试验采取单调分级(10 kN/级)加载至试验梁剪跨破坏。加固梁试验是单调分级加载至斜裂缝最大宽度为0.1 mm后,持荷状态下粘贴双L形箍板加固并达到要求后,再单调分级(10 kN/级)加载至试验梁剪跨破坏。
(4)试验测试内容
在试验梁跨中部位、支座部位设置的百分表,观测在试验荷载作用下试验梁的挠度;采用裂缝宽度观测笔测量混凝土裂缝。
应变测量内容包括箍筋应变和钢板应变。双肢箍筋一肢1/2梁高处和L形箍板表面布置应变测点(见图4)。
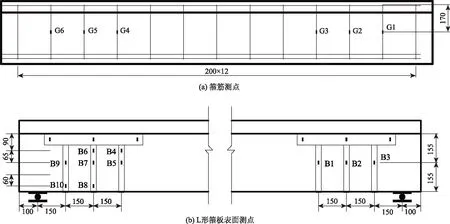
图4 钢筋和L形钢箍板应变片粘贴位置示意图(单位: mm)Fig.4 Schematic diagram of sticking positions strain gauges on steel bars and L-shaped steel hoop plate (unit: mm)
1.2 试验结果
1.2.1 参照梁PCT-0
(1)参照梁受力过程与破坏形态
P=187 kN时,试验梁左半跨的剪跨区出现第1条斜裂缝,长度约150 mm,宽度0.05 mm;加载至277 kN时,剪跨区出现第1条裂缝宽度为0.45 mm的主要斜裂缝;随着荷载的增加,剪跨区的斜裂缝缓慢发展;直到加载至460 kN时,左右剪跨区分别生成明显的主裂缝,箍筋随之屈服;加载至P=470 kN 时,左半跨主斜裂缝最大宽度已达到1.5 mm,并且主斜裂缝长度迅速向试验梁的分配梁作用位置延伸(见图5),梁体发生剪压破坏。
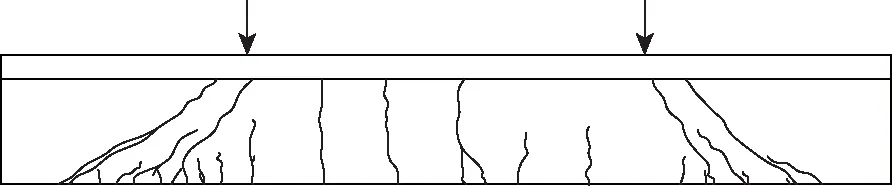
图5 试验梁PCT-0破坏时的裂缝形态Fig.5 Crack mode of damaged test beam PCT-0
(2)箍筋实测应变变化
对测试有效的G5,G6测点结果进行分析。加载初期尽管梁体表面出现了混凝土斜裂缝,测点G5,G6(见图4)的实测应变都很小且为压应变;P=277 kN时形成的主斜裂缝贯通测点G5,G6所在箍筋,测点实测应变突然增大且为拉应变,箍筋应变测点G5距离斜裂缝最大宽度处较近,故应变变化比应变测点G6要大。随着试验梁加载增加,主斜裂缝宽度继续增大,箍筋测点G6和G5的实测拉应变呈近似斜直线变化,当试验梁剪压破坏时,箍筋测点G5已屈服,测点G6未屈服。

图6 实测荷载-箍筋应变(PCT-0)Fig.6 Measured curves of load vs. stirrup strain (PCT-0)
1.2.2 PCT-1试验梁
(1)试验梁受力过程与破坏形态
P=190 kN时,试验梁左半跨的剪跨区出现一条梁表面混凝土斜裂缝(该裂缝后成为梁左半跨的混凝土主斜裂缝),最大宽度0.05 mm;加载到P=221 kN 时,该斜裂缝宽度达到0.10 mm,停止加载,保持荷载并按本次试验梁粘贴钢板的设计和施工要求,进行双L形钢板箍粘贴加固。
双L形钢板箍加固养护7 d,在粘胶达到养护要求后再进行第2阶段加载。
P=292 kN时,剪跨区第1条主斜裂缝生成。裂缝宽度为0.4 mm;随着荷载增加,裂缝缓慢发展和新生成;P=382 kN时,剪跨区箍筋开始屈服;P=523 kN时,剪跨区钢板开始屈服;P=586 kN时,梁左半跨主斜裂缝顶端(分配梁作用位置)的翼缘板混凝土压碎、底端部位混凝土拉坏,且主斜裂缝两侧有较大的混凝土错动;锚固压条弯曲变形,粘贴L形钢箍板的粘胶与梁体剥离,加固梁体发生斜截面剪压破坏(见图7)。

图7 试验梁PCT-1的裂缝形态Fig.7 Crack mode of test beam PCT-1
梁PCT-1的加载试验受力全过程中,双L形钢箍板工作良好,没有出现箍板剥离现象,只是在加固梁剪压破坏时才出现了钢箍板剥离。
(2)荷载-跨中挠度曲线
图8为参照梁与加固梁荷载-跨中挠度曲线对比图。与参照梁PCT-0的破坏荷载Pu=470 kN相比,加固梁PCT-1的破坏荷载为591 kN,提高了25.7%。未加固梁的跨中荷载-挠度曲线分为弹性段、斜裂缝生长段以及破坏段;加固梁在箍筋屈服后荷载还能进一步增加。不仅如此,由于双L形钢板箍对斜裂缝开展的约束作用,加固梁的结构整体刚度有所提升。

图8 参照梁与加固梁荷载-跨中挠度曲线Fig.8 Curves of load vs. mid-span deflection of reference beam and reinforced beam
(3)箍筋实测应变
图9为试验梁PCT-1剪跨区段箍筋应变测点G5和G6的实测的荷载-箍筋应变曲线。

图9 实测荷载-箍筋应变(PCT-1)Fig.9 Measured load vs. stirrup strain (PCT-1)
由图9可见,粘贴双L形钢板箍加固带损伤的预应力混凝土梁剪压破坏时,各道箍筋应力并不均匀,试验表明,与混凝土主斜裂缝相交的箍筋(测点G5和G6所在箍筋)已经屈服。
(4)双L形钢箍板的实测应变
图10为双L形钢箍板应变随荷载变化情况。可以看出,应变测点B1所在钢箍板基本位于梁主斜裂缝顶端正截面处,P=305~523 kN过程中,B1实测应变维持在拉应变200~320 με,到P=523 kN后实测拉应变增加到450 με并维持到梁剪压破坏。

图10 试验梁荷载-钢箍板应变曲线Fig.10 Curves of load vs. strain steel hoop plate
P=523 kN时,应变测点B2已屈服。P=586 kN前测点B3实测拉应变为1 025 με时,梁剪压破坏,应变测点B3实测拉应变急剧下降接近0。
图11为不同荷载状态下纵向各钢板的应变分布情况。由试验结果可知,加固试验梁破坏时,位于剪跨段斜截面上的各道L 形钢板箍的各测点应变表现出不均匀性,表现出各加固钢板强度发挥程度不一致,且加固后试验梁加载量越大时,各道钢箍板上测点实测拉应变的不均匀性越发明显。

图11 试验梁PCT-1钢板应变Fig.11 Strains of steel plate of test beam PCT-1
2 双L形钢板箍粘贴加固预应力混凝土梁的非线性有限元分析
2.1 钢板箍粘贴加固预应力混凝土梁有限元模型的建立
利用ABAQUS软件建立试验梁的三维(3D)有限元模型(FEM),考虑对称性,仅建立了1/4模型。有限元模型见图12,施加位移荷载直至破坏。

图12 有限元模型Fig.12 Finite element model
混凝土的建模使用了ABAQUS中的C3D8R单元;钢板亦使用C3D8R单元;普通钢筋和预应力钢筋为T2D2杆单元,内嵌到混凝土单元中。
2.2 混凝土塑性损伤本构关系
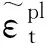
E=(1-d)E0,
(1)
式中,E0为材料无损初始弹性模量;d为损伤因子。
在单轴拉伸和压缩荷载作用下的应力-应变转换关系为:
(2)
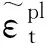
混凝土单轴拉压应力-应变关系如图13所示。

图13 混凝土单轴应力-应变关系Fig.13 Concrete uniaxial stress vs. strain
钢筋和钢板采用理想弹塑性模型。
2.3 有限元模型的验证
图14将荷载-挠度关系曲线和加固梁荷载-箍筋应变的计算结果和试验结果进行了对比,可以看出,未加固梁的对比结果吻合较好, 加固梁粘贴钢板进一步加剧了计算的复杂性,但计算结果基本能反映结构受力的变化。

图14 试验和有限元模型对比Fig.14 Comparison of test and finite element model
2.4 双L形钢板箍拉应力分布的模拟分析结果
分别对钢板厚度、混凝土强度、钢板间距、钢板宽度、剪跨长度、箍筋间距、预应力等7项参数进行分析,建立16个数值模型。
对于钢箍板加固梁,在剪切裂缝张开位置钢板拉应力较大,因此选取沿裂缝扩展方向钢板节点(见图15)并进行钢箍板横截面拉应力分析。
对预应力混凝土梁粘贴双L形箍板加固进行的试验研究表明,粘贴钢箍板加固的预应力混凝土梁斜截面破坏时,斜截面范围内钢板测点拉应变分布不均匀现象明显,一般采用不均匀系数ψvb来描述。为了能在有限元分析和试验中钢箍板应变测试结果分析中得到不均匀系数的定量值,本研究采用如下表达式定义预应力混凝土梁加固钢箍板的ψvb值:
(3)
式中,Δσi为钢箍板测点最大拉应力(或拉应变)与屈服应力(或屈服应变)之比;n为斜截面范围内钢箍板的数量。
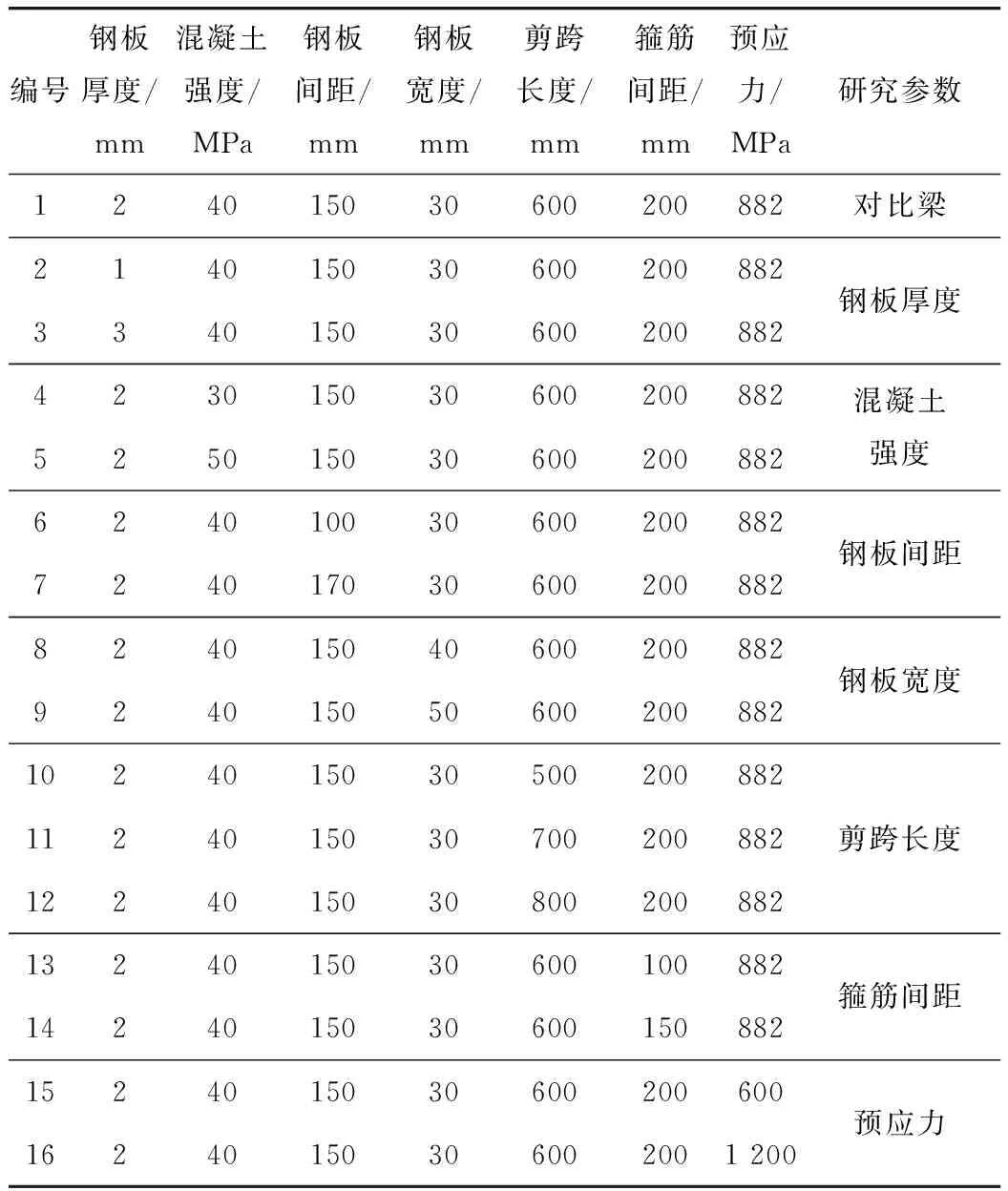
表2 计算参数Tab.2 Calculation parameters

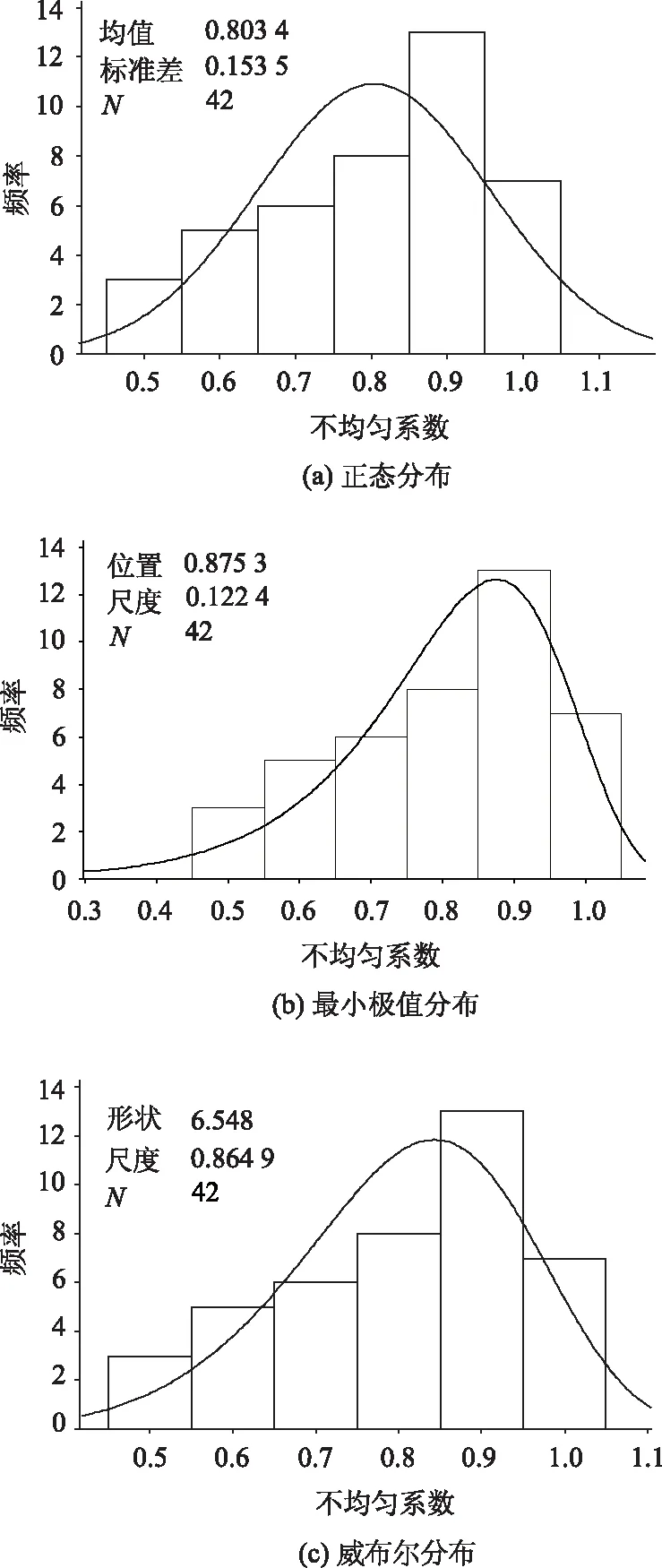
图16 概率分布直方图Fig.16 Probability distribution histogram

图17 累积概率密度比较Fig.17 Comparison of cumulative probability densities
3 加固预应力混凝土梁的抗剪承载力
抗剪承载力可以采用原梁斜截面抗剪承载力与粘贴钢箍板的抗剪承载力叠加的计算模式,抗剪承载力Vu为:
Vu=Vbo+Vb,sp,
(4)
式中,Vbo为加固前梁的斜截面抗剪承载力;Vb,sp为粘贴钢箍板加固后梁斜截面抗剪承载力的提高值,按下列公式计算:
Vb,sp=ψvbfspAb,sphsp/ssp,
(5)
式中,fsp为钢箍板的抗拉设计强度;Ab,sp为配置在同一截面处钢板截面面积之和,hsp为粘贴钢板与梁侧面混凝土粘结的竖向高度;ssp为粘贴钢板的间距。
加固梁PCT-1实测各箍板的最大拉应变分别为450 με(靠跨中部位箍板),2 405 με(中间箍板)和1 025 με,钢箍板的屈服应变为εb=fy/E=464/2.1 e5=2 210 e-6,计算得到ψvb=0.55,数值模拟和试验得出的不均匀系数ψvb一致。
下面以本研究及其他研究文献的室内模型梁[8]的试验结果,现取钢箍板的应力不均匀系数ψvb=0.55,来验证粘贴竖向钢板箍预应力混凝土梁后斜截面抗剪承载力计算方法。
对公路桥梁,加固前梁的斜截面抗剪承载力Vbo应采用规范[21]规定公式计算。对于试验梁,即使采用实测的材料参数和截面尺寸,采用设计规范公式计算的斜截面抗剪承载力Vb0也小于试验得到的实测值V′b0,一般情况下,V′b0/Vb0大约为1.4~1.7,粘贴钢箍板加固后的预应力混凝土梁斜截面抗剪承载力计算值与试验值(受剪破坏荷载)也应控制在这个差异比内。考虑差异比例为1.5时,预应力混凝土试验梁斜截面抗剪承载力推算值与试验值对比见表3。可以看出,由式(4)和式(5)且取钢箍板的应力不均匀系数ψvb=0.55计算的加固预应力混凝土斜截面抗剪承载力与试验结果比较接近。
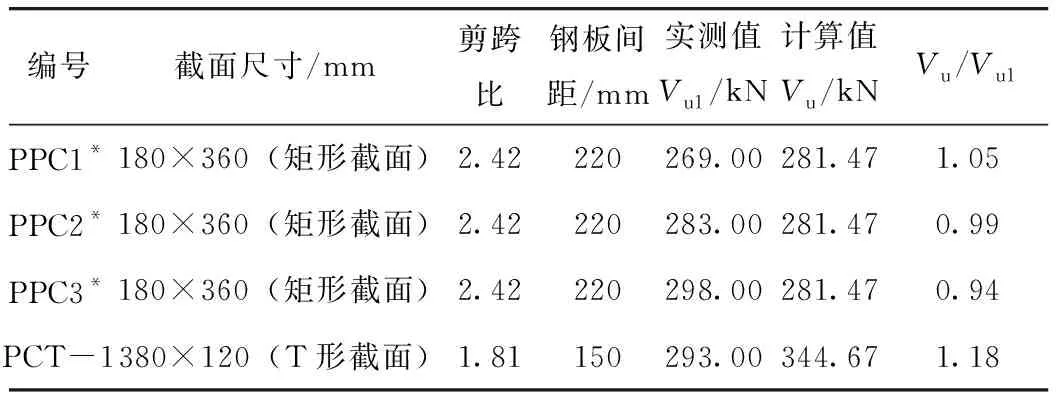
表3 加固梁抗剪承载力实测值与推算值比较Tab.3 Comparison of measured value and calculated value of shear capacity of strengthened beam
4 结论
(1)在钢箍板粘贴加固构造措施符合要求条件下,粘贴竖向钢板箍能提高已有损伤的预应力混凝土梁斜截面抗剪承载力。
(2)试验梁受力全过程和斜截面破坏试验现场观察表明,粘贴的双L形钢箍板工作良好,没有出现粘贴箍板剥离现象,在加固梁剪压破坏时钢箍板剥离。
(3)加固试验梁破坏时,位于剪跨段斜截面上的U 形钢板箍的各测点应变表现出不均匀性,且加固后试验梁加载量越大时,各道钢箍板上测点实测拉应变的不均匀性越发明显,体现出各加固钢板强度发挥程度不一致。
(4)竖向双L形钢板加固预应力混凝土T梁抗剪承载力时,钢板应力不均匀系数服从威布尔分布,95%下限取值为0.55。
