岩质边坡风化层的关键滑动面及其稳定性研究

钱 健，阮晓波，龚永康

(1.中交上海航道勘察设计研究院有限公司，上海 200120；2.合肥工业大学 汽车与交通工程学院，安徽 合肥 230009)

0 引言

岩质边坡由于风化作用通常会在基岩外部产生一层风化层。风化层一般是由残坡积层、全风化层、强风化层构成的类土质边坡的岩土结构，其岩土体的特征是十分破碎，土石混杂，分选性差,粒间结合力差,透水性强，常常被称为“土石混合体”、“类土岩”[1]。在分析风化层的稳定性时，将其岩土体看作为均质的类土体；而由于基岩的存在，风化层的破坏将不同于一般的土质边坡。因而，传统的分析方法将不能直接用于风化层稳定性的分析。

对于均质材料的土质边坡来说，采用对数螺旋线滑动面近似边坡极限破坏的最危险滑动面更为合理[2]。这是由于，作用于对数螺旋线滑动面上的每一点上的法向应力与切向应力的摩擦角部分的合力通过定义对数螺旋线的极点，使得此部分合力对于极点的力矩为零。这样建立的力矩平衡方程只有安全系数是未知量，从而不需要更多的假定便可以得到安全系数的解。在这里，我们将此种方法称为“对数螺旋线法”。此方法已经被广泛应用于边坡稳定性分析[3-5]、主动土压力计算[6-8]以及加筋土结构物设计[9-15]。然而，将此种方法用于评价岩质边坡风化层的稳定性，目前尚未见报道。

本研究主要研究岩质边坡风化层的稳定性，基于现有的对数螺旋线法，考虑到基岩的一般稳定性，改进现有方法，建立相应的风化层稳定性分析计算模型。此计算模型可以综合考虑风化层的几何外形参数岩土体的力学特性参数，通过MATLAB程序的编写运行，获取不同参数条件的安全系数值与关键滑动面，将分析这些参数对风化层稳定性及关键滑动面的影响。

1 风化层稳定性分析计算模型

1.1 基本假定

岩质边坡风化层示意图如图1所示。区域D1D2D3D4表示风化层，D1D2表示坡面，D2D3表示坡肩，H表示边坡高度，HL表示风化层在坡肩顶处的宽度，a表示坡顶坡角，w表示坡角，w0表示基岩边坡坡角。

图1 岩质边坡风化层示意图Fig.1 Schematic diagram of weathering layer of rock slope

为了能够顺利地建立分析岩质边坡风化层稳定性的计算模型，有必要事先做一些合理的假定。具体假定如下：

(1)风化层是类土体，是均质的库伦材料，破坏满足摩尔-库伦强度准则；

(2)基岩是稳定的，且其边坡坡面水平；

(3)关键滑动面在风化层内部沿着对数螺旋线滑动面在坡顶过D2D3范围内且过坡角(点D1)。

1.2 力矩平衡方程

对数螺旋线破坏体进行极限平衡分析，建立力矩平衡等式。对数螺线破坏体的极限平衡分析示意图见图2,ZC为张裂缝深度，且已知；ψ=tanφ/FS；φ为覆盖层岩土体的内摩擦角；FS为作用于滑动面上的安全系数。对数螺旋线滑动面在极坐标系中的表达式为[16]:

R=Ae-ψβ，

(1)

式中，R为极点到对数螺旋线滑动面上某一点的矢径；β为对数螺线滑动面上某一点在极坐标系中的角度；A称为对数螺旋线常量，由过点D1和点E的对数螺旋线滑动面决定的。

图2 岩质边坡风化层受力分析Fig.2 Force analysis of weathered layer of rock slope

对极点O(xc,yc)写出对数螺线破坏体极限平衡的力矩平衡等式，具体如式(7)所示：

MC=MW，

(2)

式中，MW为对数螺旋线破坏体自身重力W产生的力矩；MC为对数螺旋线滑动面上的总黏聚力产生的力矩。

式(2)中的力矩MW是驱使风化层发生破坏的驱动力，而力矩MC是抵抗风化层发生破坏的抵抗力矩。MW是可以通过修改Ebrahimi[17]的推导结果得到，具体如式(3)所示：

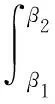
γ[(ZC-H+Y1)cotα(H-Y1)]

γ(ZC-H+Y1)2cotα[Ae-ψβ2sinβ2-

(3)

式中,γ为风化层岩土重力密度;Y1=Ae-ψβ1cosβ2-Ae-ψβ2cosβ2。

然而，MC通过Vahedifard等[18]推导及Ruan等[14]重新整理得到，具体如式(4)所示：

(4)

式中c为风化层岩土体黏聚力。

对于对数螺旋线常量A的求解，可以通过分析图2中对数螺旋线破坏体的几何外形特性得到。

即：A=[H-ZC-H(cotωtanα)]/{e-ψβ1(cosβ1+

sinβ1tanα)-e-ψβ2(cosβ2+sinβ2tanα)}。

(5)

1.3 安全系数隐函数方程

通过力矩平衡关系，如式(2)所示，结合式(3)和式(4)，可以推导出关于安全系数FS的隐函数方程式，具体如下式所示：

γ[(ZC-H+Y1)cotα(H-Y1)][Ae-ψβ2sinβ2-

(6)

1.4 安全系数求解

为了使所求得的安全系数值在理论上是合理的，编制程序求解的时候，需要给出一定的判断条件来排除不合理的值，具体判断条件如下：

(1)A>0；

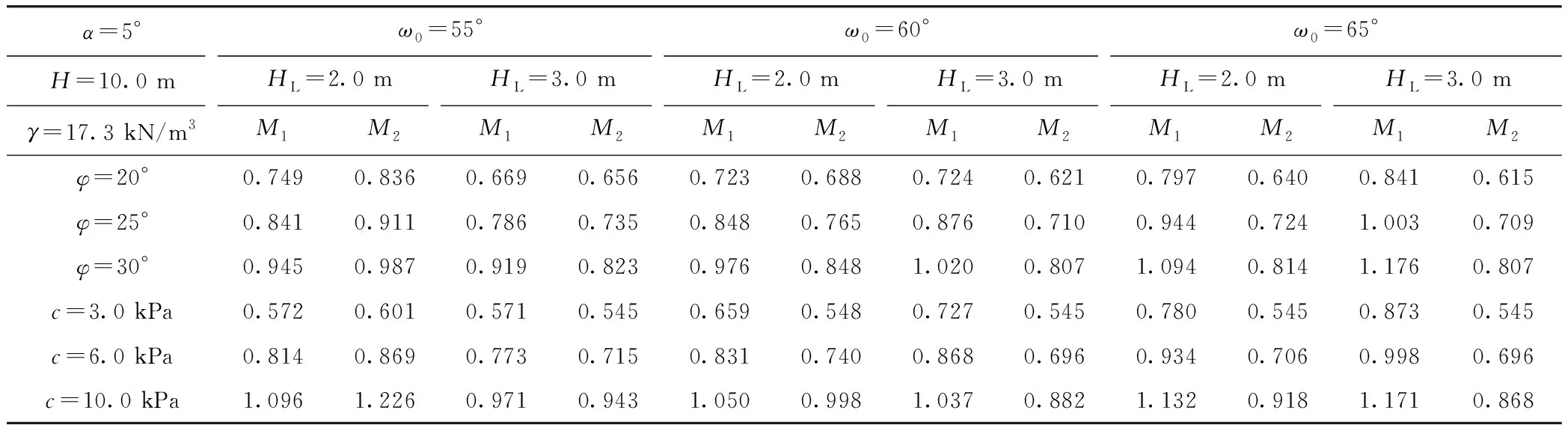
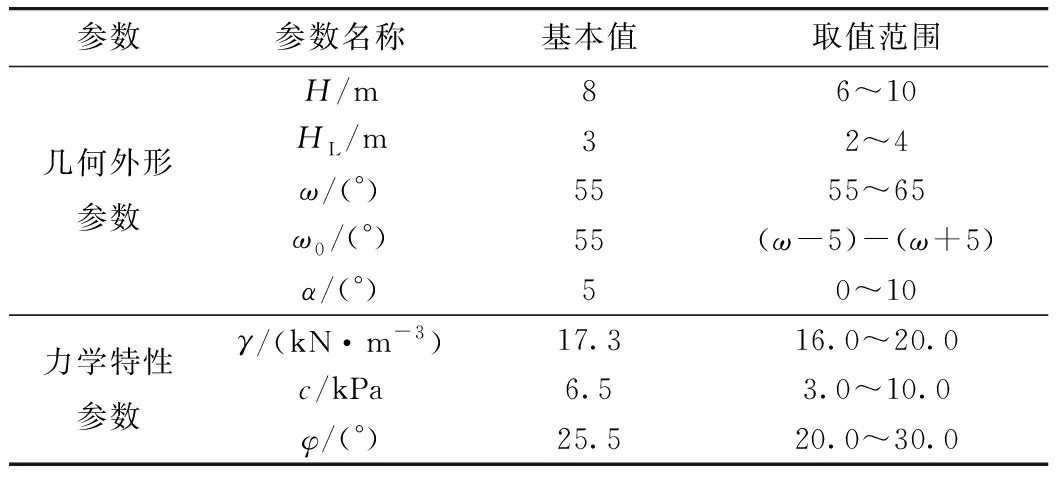
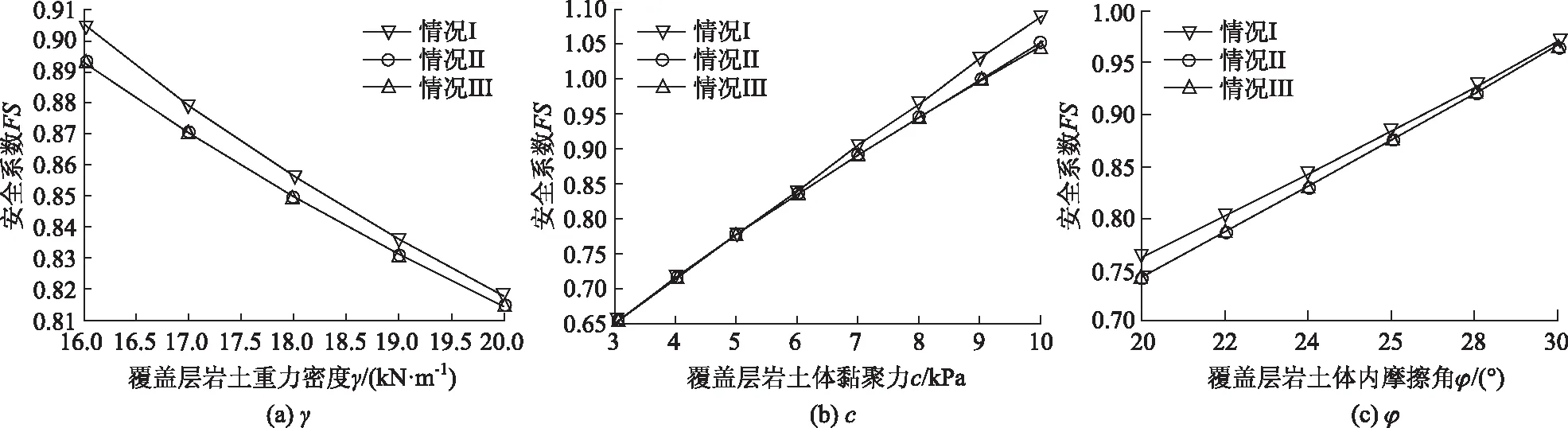
(2)X1>0且X1

(3)|FG|>|KG|，其中，|FG|=Ae-ψβ1sinβ1-Ae-ψβsinβ，|KG|=[(Ae-ψβsinβ-Ae-ψβ1sinβ1)-[(Hcotω+HL)-(H+HLtanα)cotω0]tanω0。

满足判断条件(1)是显而易见。满足判断条件(2)是为了对数螺旋线滑动面能够出现在边坡坡顶范围内。满足判断条件(3)是为了使对数螺旋线滑动面不至于和基岩边坡坡面相交，如图3所示 。通过MATLAB软件编制求解安全系数FS的计算程序，下面给出了计算程序编制的流程图，如图4所示，其中FS表示迭代计算过程中的安全系数计算值。

图3 判断条件(3) 所需满足的情形示意图Fig.3 Schematic diagram of circumstance of judgment condition (3) need to be met

2 与双楔体法对比分析

为了验证本研究方法(M2)的合理性，将其计算的安全系数与传统的双楔体法(M1)计算的结果进行对比分析。参数的基本取值如下：边坡高度H=10.0 m，张裂缝深度ZC=0，坡顶坡角α=5°，边坡坡角ω=60°，风化层岩土体重力密度γ=17.3 kN/m3，风化层岩土体内摩擦角φ=25.5°，风化层岩土体黏聚力c=6.5 kPa。当采用双楔体法计算安全系数时，假设风化层岩土与基岩或者地基的界面摩擦角和黏聚力分别等于风化层岩土体的内摩擦角和黏聚力。

图4 计算安全系数FS的流程图Fig.4 Flowchart of calculating safety factor FS

本研究方法与双楔体法计算的不同情况下的安全系数如表1所示。从表中可以看出，当ω0=55°，HL=2.0 m时，双楔体法计算出的安全系数小于本研究方法计算的结果，因而此时岩质边坡风化层的关键破坏模式是沿着基岩边坡坡面及地基表面滑动的平移破坏模式。然而，随着风化层在坡肩顶处宽度或者基岩边坡坡角的增加，岩质边坡风化层的失稳将发生在其内部。若此时岩质边坡风化层的岩土体接近均质的库伦材料，按照本研究方法计算风化层的安全系数在一定程度上是合理的。

表1 本研究方法与双楔体法计算安全系数对比Tab.1 Comparison of safety factors obtained from proposed method and double-wedge method

3 影响因素分析

为了分析不同参数对岩质边坡风化层稳定性的影响，首先给出了参数分析中所需参数的基本值和其变化范围，具体如表2所示。并且在参数分析中考虑了3种不同情况下边坡几何外形参数对安全系数FS的影响,即情况I：ω=55°，ω0=50°；情况Ⅱ：ω=55°，ω0=55°；情况Ⅲ：ω=55°，ω0=60°。此外，同时分别考虑ZC=0和ZC=2.0 m的情形。

表2 参数分析中的基本取值与变化范围Tab.2 Basic values and its ranges their for parameter analysis

3.1 几何外形参数对FS的影响

首先，分析当ZC=0时的情形。边坡高度H对安全系数FS的影响如图5(a)所示，当H从6 m变化到10 m时，在情况Ⅰ到Ⅲ的条件下，FS分别减小了15.66%，19.26%和19.39%。此时，在情况Ⅲ条件下，H对FS的影响程度最大。风化层在坡顶处的宽度HL对FS的影响如图5(b)所示，当HL从2.0 m变化到4.0 m时，在情况Ⅰ到Ⅲ的条件下，FS分别减小了14.92%，3.84%，0.65%；可以说情况Ⅰ条件下，HL对FS的影响程度最大。坡顶倾角α对FS的影响如图5(c)所示，当α从0变化到10°时，在情况Ⅰ到Ⅲ的条件下，FS分别增加了2.26%，减小了0.28%和0.28%。可以看出，情况Ⅰ条件下FS随α的变化趋势不同于另外两种情况下的，这也许是因为此种情况下发生了平移破坏，从而导致用本研究方法计算的FS偏大。边坡坡角α对FS的影响如图5(d)所示，当ω从55°变化到65°时，在情况Ⅰ到Ⅲ的条件下，FS分别减小了16.75%，16.01%，16.01%。可以看出，在情况Ⅰ条件下，ω对FS的影响程度最大。基岩边坡坡角ω0对FS的影响如图5(e)所示，当ω0从45°变化到65。时，FS减小了11.77%；当ω0=53°时，FS则不再变化，这主要是因为关键滑动面不再受基岩坡面的影响。然而，当ZC=2.0 m时，从图5中可以看出，安全系数随几何参数的变化趋势与ZC=0时一致，而存在张裂缝时安全系数明显偏小。

图5 不同情况下几何外形参数对FS的影响Fig.5 Influence of geometric parameters on FS in different cases

从上面的结果可以看出，随着边坡高度或者坡顶坡角变化，基岩边坡坡角的增大对FS影响的变化将减弱；当风化层在坡顶处的宽度或者边坡坡角增大到某一值时，基岩边坡坡角的变化对FS的影响可以忽略；在特定的边坡坡角条件下，当基岩边坡坡角增加到某一值时，FS将不再随其变化而变化，这说明此时风化层的失稳不再受基岩边坡存在的影响。

3.2 岩土体力学特性参数对FS的影响

首先，分析无张裂缝影响的情形，即ZC=0。风化层岩土体重力密度γ对安全系数FS的影响如图6(a)所示，当γ从16.0 kN/m3变化到20.0 kN/m3时，在情况Ⅰ到Ⅲ的条件下，FS分别减小了9.60%，8.80%和8.80%；可以看出，在情况I条件下，γ对FS的影响程度最大；而情况Ⅱ和Ⅲ条件下的影响程度相当。风化层岩土体黏聚力c对FS的影响如图6(b)所示，当c从3.0 kPa变化到10.0 kPa时，在情况Ⅰ到Ⅲ的条件下，FS分别增加了67.17%，61.46%和60.97%。可以看出，在情况I条件下，c对FS的影响程度最大。风化层岩土体内摩擦角φ对FS的影响如图6(c)所示，当φ从20.0°变化到30.0°时，在情况Ⅰ到Ⅲ的条件下，FS分别增加了27.60%，30.46%和30.50%。可以看出，在情况Ⅲ条件下，φ对FS的影响程度最大，但与情况Ⅱ条件下的情形差别不大。综合上面的分析可以看出，不论在岩土体重力密度条件下，还是在黏聚力或者内摩擦角条件下，随着基岩边坡坡角的增大，其对FS影响程度的变化将减弱。然而，当ZC=2.0 m时，安全系数随力学特性参数的变化趋势与ZC=0时一致，并且和图5中的情况一样，张裂缝存在会导致安全系数减小。

图6 不同情况下岩土体力学特性参数对FS的影响Fig.6 Influence of rock-soil mechanical characteristic parameters on FS in different cases

3.3 关键滑动面分析

3.3.1φ对关键滑动面的影响

为了分析风化层岩土体内摩擦角φ对关键滑动面的影响，首先给定一些基本的参数值，具体如下：边坡高度H=10 m，张裂缝深度ZC=2.0 m，边坡坡角ω=60°，风化层岩土体黏聚力c=6.5 kPa。并且考虑3种情况：情况I，φ=20.0°；情况Ⅱ，φ=25.0°；情况Ⅲ，φ=30.0°。

当HL=2.0 m，ω=60°，ω0=55°时，φ对关键滑动面的影响如图7(a)所示，可以看出，随着φ的增加，关键滑动面在底部更接近基岩边坡坡面。当ω0增加到60°时，φ对关键滑动面的影响如图7(b)所示，此时情况Ⅰ、Ⅱ及Ⅲ条件下的关键滑动面非常接近。当ω0再增加到65°时，φ对关键滑动面的影响如图7(c)所示，与图7(b)的情形相似，情况Ⅰ、Ⅱ及Ⅲ条件下的关键滑动面也是比较接近的。

当HL=3.0 m，ω=60°，ω0=55°时，φ对关键滑动面的影响如图7(d)所示，关键滑动面的情形如图7(a)所示；当ω0增加到60°时，φ对关键滑动面的影响如图7(e)所示，情况Ⅱ和Ⅲ条件下的关键滑动面不受基岩边坡的影响。当ω0再增加到65°时，φ对关键滑动面的影响如图7(f)所示，可以看出，随着φ的增加，关键滑动面远离基岩边坡坡面，将不受基岩边坡存在的影响。

图7 φ对关键滑动面的影响Fig.7 Influence of φ on critical slip surface

通过关键滑动面的观察，还可以发现，随着基岩边坡坡角的增大，关键滑动面与基岩边坡坡面最接近处在往坡顶移动，这有助于获得最大的破坏体体积以获得最小FS值。

3.3.2c对关键滑动面的影响

为了分析风化层岩土体黏聚力c对关键滑动面的影响，首先给定一些基本的参数值，具体如下：边坡高度H=10 m，张裂缝深度ZC=2.0 m，边坡坡角ω=60°，风化层岩土体内摩擦角φ=25.5°。并且考虑3种情况：即情况I，c=3.0 kPa；情况Ⅱ，c=6.0 kPa；情况Ⅲ，c=10.0 kPa。

当HL=3.0 m，ω=60°，ω0=55。时，c对关键滑动面的影响如图8(d)所示，关键滑动面的情形相似于图8(c)。当ω0增加到60°时，c对关键滑动面的影响如图8(e)所示，可以看出，情况Ⅰ和Ⅱ条件下关键滑动面不受基岩边坡的影响。当ω0再增加到65°时，c对关键滑动面的影响如图8(f)所示，可以看出，情况Ⅰ，Ⅱ和Ⅲ条件下的关键滑动面不受基岩边坡的影响。

图8 c对关键滑动面的影响Fig.8 Influence of c on critical slip surface

综合以上分析发现，随着基岩边坡坡角的增大，关键滑动面与基岩边坡坡面最接近处往坡顶移动；同时，较小的岩土体黏聚力条件下，关键滑动面不易受基岩边坡存在的影响。

4 结论

本研究建立了分析岩质边坡风化层稳定性的计算模型，该模型考虑了基岩边坡的影响作用。通过力矩平衡方程的建立和求解，得到评价岩质边坡风化层稳定性的安全系数隐函数方程。最后运用MATLAB编制程序，计算出安全系数的值。

本研究的计算模型包括边坡几何外形参数、风化层岩土体力学特性参数等影响因素，并且可以分析这些参数对安全系数与关键滑动面的影响。通过参数分析，得到如下结论。

(1)风化层的几何外形参数包括：边坡高度、风化层在坡顶处的宽度、张裂缝深度、坡顶坡角、边坡坡角和基岩边坡坡角。由于基岩的影响，存在如下的情况：当不考虑张裂缝作用时，当基岩边坡坡角不小于边坡坡角时，随着边坡高度、坡顶坡角或者边坡坡角的增大，基岩边坡坡角的变化对风化层的稳定性影响不大；当风化层在坡顶处的宽度足够大时，边坡坡角和基岩边坡坡角的关系对风化层稳定性的影响可以忽略；当边坡坡角55°时，基岩边坡坡角在达到53°之后，其继续增大不再影响风化层的稳定性。然而，当考虑张裂缝作用时，风化层稳定性明显降低。

(2)风化层岩土体力学特性参数包括：风化层岩土体的重力密度、黏聚力和内摩擦角。同样是由于基岩存在影响的作用，出现如下情况：当基岩边坡坡角不小于边坡坡角时，随着风化层岩土体重力密度或者内摩擦角的增大，基岩边坡坡角的变化对风化层的稳定性影响较小；而随着风化层岩土体黏聚力的增大，基岩边坡坡角的减小有利于提升风化层的稳定性。

(3)当风化层在坡顶处的宽度较小，且基岩边坡坡角较小时，关键滑动面在上下部会不同程度的更加接近基岩边坡坡面，这是由于该情况下，岩质边坡风化层的破坏形式更可能为平移破坏。当风化层在坡顶处的宽度和基岩边坡坡角增大到某一值时，关键滑动面逐渐远离基岩边坡坡面，与一般边坡失稳时的关键滑动面情形一致，即风化层的稳定性不受基岩边坡存在的影响。