抗风缆对大跨人行悬索桥非线性静风失稳模式的影响

2022-03-21管青海李加武刘健新

公路交通科技 2022年2期

管青海，李加武，刘健新

(1.山东建筑大学交通工程学院，山东济南 250101；2.长安大学陕西省公路桥梁与隧道重点实验室，陕西西安 710064；3.长安大学风洞实验室，陕西西安 710064)

0 引言

大跨缆索桥梁受强风荷载可能发生动力失稳，也可能发生静力失稳，甚至风致静力失稳还可能会先于动力失稳。先前研究表明明石海峡大桥(设计主跨1 990 m)静风失稳计算风速(76.5 m/s)远低于风洞试验颤振临界风速(92 m/s)[1]，最近研究发现2×1 500 m双主跨斜拉桥也存在静风失稳与颤振发散的竞争关系[2]。近几年来，研究学者对大跨桥梁静风失稳问题开展了深入研究，诸如气动失稳模式、失稳发展过程、失稳机理及其对策[3-7]，以及紊流风场、非均匀风场、风偏角等因素对大跨桥梁静风稳定的影响等系列专题研究[8-11]。

抗风缆是提高桥梁结构刚度及抗风能力的重要结构措施，尤其在大跨人行悬索桥中应用广泛。研究一致发现，抗风缆可以大幅度提高桥梁颤振性能和静风失稳临界风速[12-15]，不同布置形式的抗风缆结构对大跨人行悬索桥静风失稳风速提高程度也不同[14]。虽然许多学者分析了抗风缆可以提高桥梁静风稳定性及其提高幅度，但是既往研究多集中在动力特性影响或者静风失稳临界风速单一指标，抗风缆对于悬索桥静风失稳模式的影响鲜有涉及。本研究以一座典型大跨人行悬索桥为工程分析算例，基于风洞试验与数值分析，展开抗风缆对悬索桥静风失稳形态及其发展成因的分析，研究抗风缆对大跨人行悬索桥静风失稳模式的影响。

1 桥梁非线性静风稳定理论及其数值实现方法

1.1 大跨桥梁静风稳定理论的非线性问题

桥梁非线性静风稳定分析主要涉及到材料非线性、几何非线性和静风荷载非线性等3个方面。一般而言，钢结构桥梁临界静风失稳前的钢材材料非线性问题不显著，而失稳后的桥梁可默认为完全垮塌，所以材料非线性问题一般可不予考虑。桥梁几何非线性问题需要通过循环迭代几何大变形修正刚度矩阵来实现。静风荷载非线性是由桥梁扭转位移与风荷载气动耦合引起的，是分析中最核心的非线性问题，需要对桥梁有效风攻角进行循环迭代以得到实时非线性静风荷载。大跨桥梁静风三分力荷载表达式为方程式(1)。

(1)

式中，FD(αe)，FL(αe)，M(αe)分别为静风阻力、升力与升力矩;CD(αe)，CL(αe)，CM(αe)分别为阻力系数、升力系数与升力矩系数，静风三分力及其系数均是有效风攻角αe的函数；有效风攻角αe为结构静风扭转角与来流风攻角之和；ρ为空气密度，本研究取1.25 kg/m3，U为计算风速，1/2ρU2为来流动压。

大跨桥梁静风失稳问题是在非线性静风荷载几何大变形下的非线性问题，即求解方程式(2)。

([KL(δj-1)]+[Kσj-1(δj-1)]G+W)×{Δδj}=

{Rj(Ui,αj)}-{Rj-1(Ui,αj-1)}，

(2)

式中，[KL(δj-1)]，[Kσj-1(δj-1)]G+W依次为第j-1迭代步的线弹性刚度矩阵、自重荷载与静风荷载(G+W)共同作用下的几何刚度矩阵；{Δδj}为第j迭代步的结构位移增量；{Rj-1(Ui,αj-1)}、{Rj(Ui,αj)}为静风速Ui下第j-1迭代步对应有效风攻角αj-1、第j迭代步对应有效风攻角αj的静风荷载，计算式参见式(1)。

1.2 桥梁非线性静风稳定分析方法

桥梁非线性静风响应计算，需要采用增量法求解方程式(2)，一方面是方程式自身需要迭代计算，另一方面需要对风速分级逐步增量迭代计算以得到每级风速响应，所以实现非线性静风稳定分析要选取双层增量迭代范式。

风攻角正负取决于风荷载方向和结构扭转位移方向，设风荷载方向取结构总体坐标系正方向，根据右手螺旋法则，正向风攻角定义为使结构产生逆时针扭转位移趋势的来流风向。具体分析过程概要总结如下。

(1)求解初始自重状态，为后续各级风荷载计算计入自重效应；

(2)根据主梁空间位移得到当前风速工况下的有效风攻角，计算本级风速静风荷载，除主梁需要计算静风三分力荷载之外，其余非主梁构件，主塔和缆索等构件均只考虑静风阻力荷载，其阻力系数可以参考相关抗风规范选取；

(3)启用应力刚化，采用N-R迭代方法计算该级风速下的非线性响应；

(4)判断计算步骤(3)敛散性，若发散，则缩短风速步长，返回步骤(2)重新计算，若收敛，则将初始风攻角叠加主梁扭转角以更新有效风攻角；

(5)判定静风荷载敛散性，判定规则为主梁位移范数或主梁静气动力系数范数在有限次数内是否收敛于0，若收敛，则增加风速进行下一级风速计算，如发散，则前一级风速为静风失稳临界风速，一般临近失稳风速时，需缩短风速增量，以求得满足风速精度的临界失稳风速。

2 工程背景及主梁静三分力系数

2.1 大桥基本概况及有限元模型

以一座420 m主跨人行悬索桥为工程分析算例。大桥地处山东省临沂市费县某开发景观山区，横跨最大纵深140 m左右的深峡谷，峡谷风效应显著。为(38+420+47.5)m跨径组合的双塔单跨钢结构悬索桥，吊杆间距为3 m，主梁为纵横型钢梁加角钢斜撑结构，横向平铺3块10 cm厚的混凝土桥面板，主梁两端加设小风嘴，防护栏杆高1.75 m，栏杆防护网透风率高达70%，主梁全宽4.0 m。

该桥属于主梁宽跨比很小的典型窄桥，为提高结构刚度与抗风能力，大桥主梁两侧设置了倾角范围35°～53°的抗风缆，共布置57对抗风拉索，抗风拉索间距为6 m，受限于地形地质条件，抗风缆4个锚固端位置略有不对称，而且跨中两侧抗风拉索数量不同，抗风拉索纵向布置并不对称，抗风缆平面布置示意如图1所示。

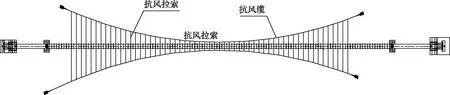
图1 抗风缆平面布置Fig.1 Plane layout of wind-resistant cables

建立全桥结构有限元模型，采用梁单元模拟主梁与桥塔等梁式结构，采用杆单元模拟主缆、抗风缆、吊杆与抗风拉索等缆索结构，采用质量单元模拟索夹、栏杆、桥面铺装等附属质量构件。塔底与锚碇均采用固结约束，在塔顶处主缆与桥塔采用耦合约束。4个视角下的全桥有限元模型见图2。

图2 四个视角下的全桥有限元模型Fig.2 FE model of bridge from 4 perspectives

2.2 大攻角区间主梁静三分力系数

山区峡谷风环境常常复杂多变，桥梁经受风攻角范围极可能较广[16]，加之大跨柔性桥梁静风扭转位移较大，附加风攻角效应显著，所以山区峡谷桥梁宜尽量取较大风攻角范围的三分力系数。为满足研究需要，本研究静三分力系数测定试验风攻角范围取为-15°～+15°，攻角变化步长取1°，1°范围内三分力系数取线性内插相邻攻角值。

在长安大学风洞实验室中进行主梁静气动力系数测定试验。节段试验模型设计几何缩尺比为1∶14，模型总高度为0.170 m，全宽为0.286 m，全长为0.866 m，试验模型两端设置椭圆薄平板来保证端部二维绕流特性，测力试验在来流风速为15 m/s的均匀风场中进行。图3给出了风轴坐标系下±15°区间范围内大桥主梁断面的静三分力系数。

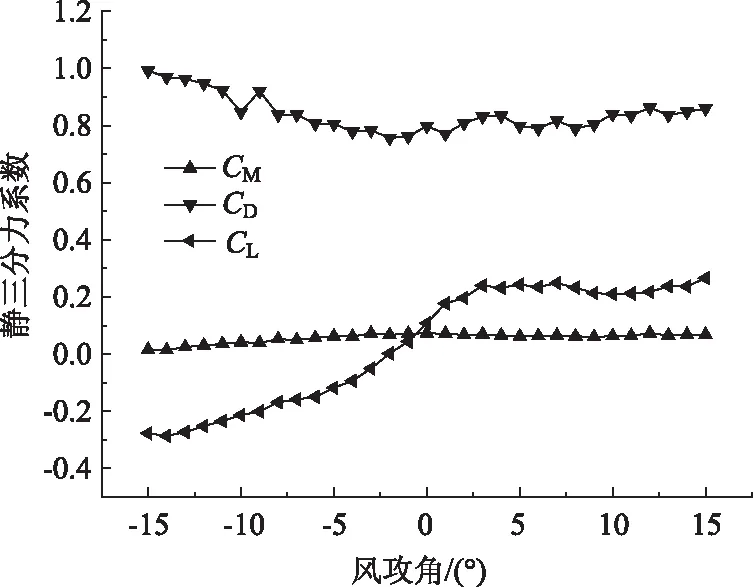
图3 主梁静三分力系数Fig.3 Aerostatic coefficients of main girder

3 抗风缆对非线性静风失稳的影响

3.1 结构动力特性

抗风缆对大跨人行悬索桥动力特性影响显著[17-18]。考虑如图1所示抗风缆结构布置，抗风缆张拉力设为1 800 kN，表1对比了大桥有无抗风缆结构的几阶关键模态动力特性。由表1可知，抗风缆结构能够大幅度提高结构体系刚度。去掉抗风缆后，大桥模态发生顺序随之发生改变，基频模态由

表1 大桥关键模态对比Tab.1 Contrast of key modes of bridge

主梁一阶反对称侧弯转变为主梁一阶正对称侧弯，原基频模态主梁一阶反对称侧弯转为第2顺位；同时各阶模态频率下降显著，其中主梁一阶反对称竖弯频率降幅34.1%，主梁一阶反对称扭转频率降幅41.4%，主梁一阶正对称侧弯频率降幅高达62.0%，这表明抗风缆结构对大桥主梁侧向、竖向和扭转刚度均有较大贡献，其中对主梁侧向刚度贡献程度最大。

3.2 主梁非线性静风位移响应及失稳形态

考虑静阵风效应影响，取静阵风系数1.37，计算法向风来流0°风攻角作用下大桥静风失稳临界风速为75 m/s，而去掉抗风缆后大桥静风失稳临界风速仅有34 m/s，降幅高达54.7%。这表明对于420 m主跨量级人行悬索桥，抗风缆结构是提高静风稳定性的强有利措施。

图4给出了抗风缆悬索桥主梁静风位移随风速变化过程:(1)主梁各向静风位移随风速增大而呈非线性增长，横桥向位移与竖桥向位移均为负值，扭转角位移为正值；(2)跨中是主梁静风位移敏感位置，主梁三向静风最大位移基本都发生在跨中位置；(3)主梁静风失稳临界状态呈现出三向位移耦合复杂变形，主梁扭转变形较大、竖向位移分量与侧向位移分量也占较大比重，是一种以扭转位移为主的三向耦合变形状态；(4)由于本桥抗风缆和抗风拉索没有满跨布置，且两端抗风拉索不对称，所以三向静风位移不严格对称，在端抗风拉索位置附近，由于抗风拉索的影响，使竖桥向位移和扭转角位移呈现正负位移变化。

图4 抗风缆悬索桥主梁静风位移Fig.4 Aerostatic displacements of main girder of suspension bridge with wind-resistant cables

图5给出了无抗风缆悬索桥主梁静风位移随风速变化过程，与图4明显不同，具体表现在：(1)主梁最大位移分量来自于横桥向，竖向位移与扭转角位移占比较小，主梁最大横桥向与竖桥向位移都发生跨中位置，最大扭转角位移大致发生在1/4桥跨；(2)主梁竖桥向位移转变为正向发展，扭转角位移转变为反对称发展；(3)主梁静风失稳临界状态为以横桥向位移为主、扭转角位移与竖桥向位移为辅的横桥向失稳；(4)去掉抗风缆后，主梁位移不再受抗风缆和抗风拉索影响，梁端竖桥向位移和扭转角位移的正负位移现象消失。

图5 无抗风缆悬索桥主梁静风位移Fig.5 Aerostatic displacements of main girder of suspension bridge without wind-resistant cable

3.3 缆索构件静风应力响应及失稳路径

受主梁静风位移影响，悬索桥缆索构件应力随之相应发生变化，而缆索构件应力松弛是悬索桥刚度失效的直接原因。所以分析缆索系统静风应力变化，可得出悬索桥系统刚度变化，继而分析悬索桥刚度丧失过程，从而研究悬索桥静风失稳原因。

总体来看，迎风侧缆索应力随风速增大而增大，背风侧主缆和吊杆应力随风速先减后增，背风侧抗风缆与抗风拉索应力均随风速增大而降低；悬索桥结构刚度失效来自于背风侧的抗风缆和抗风拉索，靠近静风失稳临界风速时，背风侧抗风缆残余应力已低于5 MPa，与初始状态相比降幅高达98%，同时背风侧抗风拉索静风应力降低了87%，背风侧抗风缆和抗风拉索基本达到完全应力松弛状态，此时桥梁结构明显濒临静风失稳。图6给出了抗风缆悬索桥跨中主缆与抗风缆的静风应力变化过程。

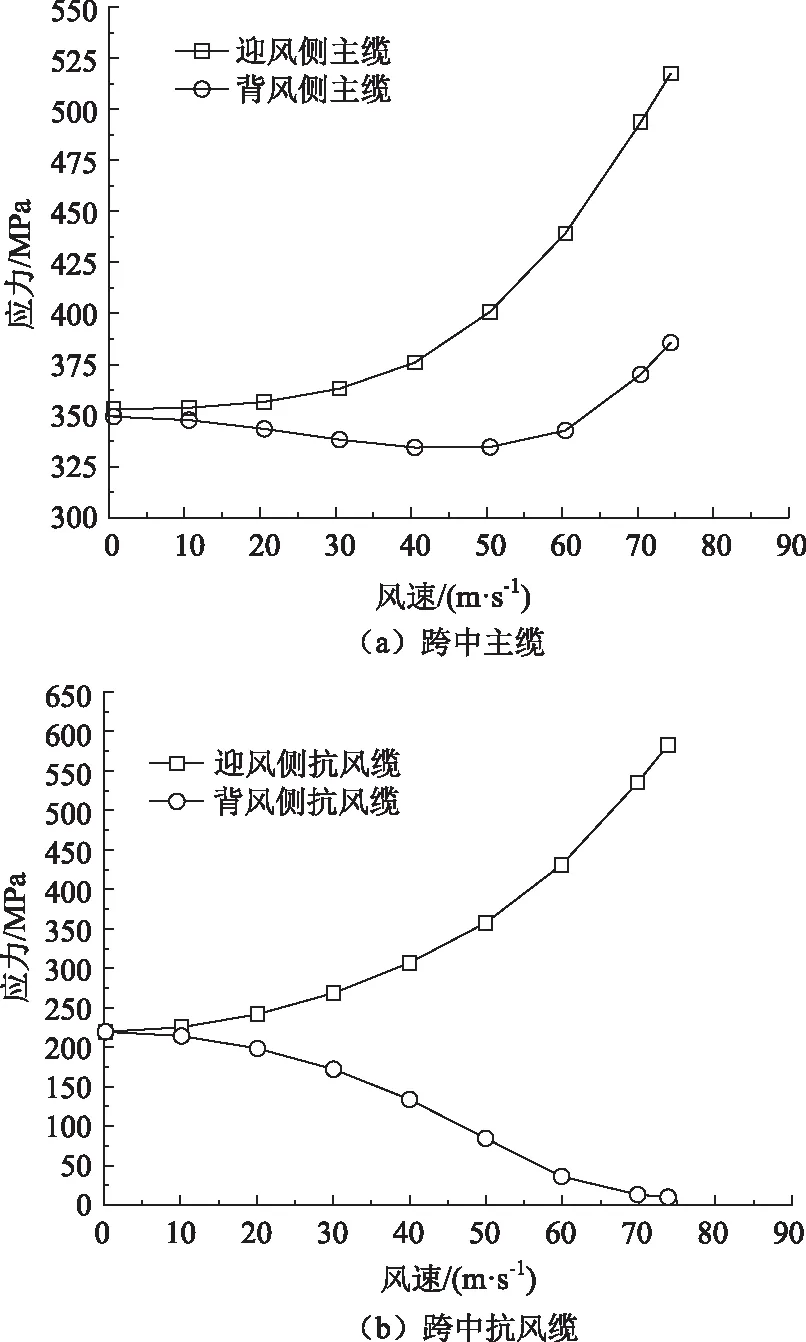
图6 抗风缆悬索桥跨中缆索静风应力Fig.6 Aerostatic stresses of mid-span cables of suspension bridge with wind-resistant cables

图7给出了无抗风缆悬索桥跨中主缆与吊杆静风应力变化过程，对比发现，无抗风缆悬索桥缆索构件静风应力变化幅度远低于抗风缆悬索桥缆索构件，且迎风侧与背风侧两侧静风应力变化方向与抗风缆悬索桥基本相反；背风侧吊杆静风应力增大，背风侧主缆静风应力基本维持不变，迎风侧吊杆静风应力轻微降低，迎风侧主缆静风应力在接近静风失稳时仅降低9.6%。这也说明无抗风缆悬索桥静风失稳时，主梁与主缆相对竖向位移较小，结构是以主梁横桥向位移为主的失稳形态。

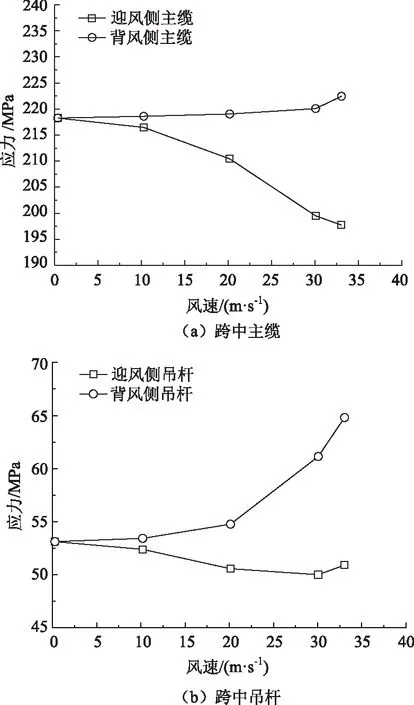
图7 无抗风缆悬索桥跨中缆索静风应力Fig.7 Aerostatic stresses of mid-span cables of suspension bridge without wind-resistant cable

3.4 非线性静风失稳致变机理

为定性分析导致大桥静风失稳的关键分量荷载，将主梁静风阻力、升力和升力矩视作独立作用变量，计算分量荷载作用下的大桥静风失稳临界风速。图8给出了抗风缆悬索桥单独静三分力分量在不同比例作用下的静风失稳临界风速，其中升力矩荷载影响程度最大，升力荷载次之，静风阻力荷载最小，这表明主梁静风升力矩是影响抗风缆悬索桥静风失稳的主要荷载，也表征该静风失稳形态为扭转变形为主的耦合失稳。在主梁静风扭转位移不断增大的过程中，主梁牵连缆索发生相对竖向位移，主梁正向发展的扭转位移使得背风侧缆索构件应力不断卸载，最终跨中抗风缆最先达到应力松弛，使得整个结构体系残余刚度难以抵抗微小风荷载增量而致失稳。值得说明的是主梁负向竖桥向位移可以提高悬索桥缆索结构重力刚度，对于静风稳定性有利，这也是抗风缆悬索桥静风失稳风速较高的原因。

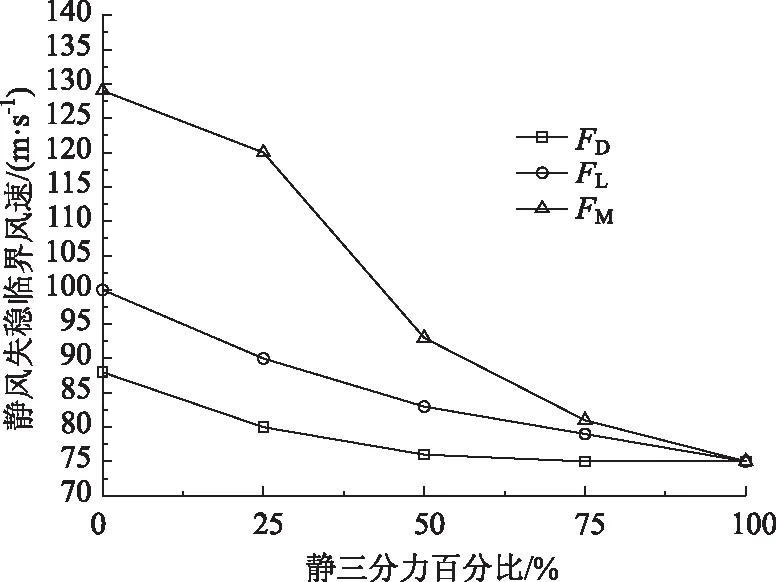
图8 抗风缆悬索桥主梁单独静三分力分量不同作用比例下的失稳临界风速Fig.8 Instability critical wind velocity of main girder of suspension bridge with wind-resistant cables under different proportions of single aerostatic component force

图9给出了无抗风缆悬索桥主梁单独静三分力分量不同作用比例下的静风失稳临界风速，与图8不同，主梁静风阻力荷载对无抗风缆悬索桥静风稳定性影响最大，升力荷载次之，而升力矩荷载几乎没有影响，这表明无抗风缆悬索桥静风失稳形态为主梁横向位移为主的屈曲型失稳，此失稳模式的缆索结构静风应力损失较小，在风速增长过程中，扭转位移与竖桥向位移增速不大，而主梁横桥向位移发展迅速，最终在过大的主梁横桥向位移作用下，悬索桥结构体系失去系统刚度而失稳。

图9 无抗风缆悬索桥主梁单独静三分力分量不同作用比例下的失稳临界风速Fig.9 Instability critical wind velocity of main girder of suspension bridge without wind-resistant cable under different proportions of single aerostatic component force