土质斜坡存在唯一最小安全系数的数据作图论证及原因分析*

岳中琦 康兴宇

(香港大学土木工程系， 香港 999077， 中国)

0 引 言

0.1 前人研究

在任何斜坡工程中，斜坡稳定性分析都是必不可少的一项工作，对定量评价斜坡安全性起极其重要的作用(陈祖煜， 2003； 陈祖煜等， 2005；Yue et al.， 2002， 2013； 岳中琦， 2015； 岳中琦等， 2014)。斜坡稳定性分析的最重要定量指标是斜坡的安全系数。因此，近百年来，众多岩土研究人员对斜坡安全系数做了大量研究和分析。首先，根据它们的力学理论基础，斜坡安全系数计算方法至少有以下3大类：第1类是基于极限平衡原理的有限条分法(Fellenius， 1936)； 第2类是强度折减法(郑宏等， 2002； 郑颍人等， 2010； 刘康琦等， 2020)； 第3类是极限分析法(Chen et al.，2012； 霍沿东等， 2019； 黄珮伦等， 2020)。本文主要是应用第1类基于极限平衡原理的有限条分法，来研究和论证土质斜坡存在唯一最小安全系数，并分析土体黏聚力和内摩擦角对斜坡安全系数作用的不同规律，从而给出斜坡存在唯一最小安全系数的土力学原因。

基于极限平衡原理的有限条分法拥有极其长久和丰富的发展历史。这些发展历史体现在自1927年以来的以下代表性论文论著：Fellenius(1936)、Janbu(1954， 1975， 2005)、Bishop(1955)、Morgenstern et al. (1965)、Spencer(1967)、Sarma(1979)、Chen et al. (1983)，Zhang et al. (2019)。这类方法是基于土体莫尔-库仑抗压剪破坏准则，假设斜坡土体内部存在一个潜在滑移面，再将潜在滑移面上部的斜坡土体划分为很多垂直细长土条。通过这些土条的静力平衡方程，得到在极限平衡条件下潜在滑移面所拥有的抵抗沿潜在滑移面下滑力的能力大小。这个抵抗能力和主动下滑力之比值就是斜坡的安全系数。抵抗能力由斜坡黏聚力和内摩擦角贡献。实际斜坡的这个比值(或安全系数)最小值是1，抵抗力与下滑力恰好平衡。稳定斜坡安全系数值都要大于1，越大越稳定安全，越小越不稳定、倾向滑坡。每个安全系数都基于一个假定的潜在滑移面。潜在滑移面拥有的安全系数越大，就越不可能沿着这个潜在滑移面发生滑坡。反之，潜在滑移面拥有的安全系数越小，就越有可能沿着这个潜在滑移面发生滑坡。

因此，斜坡稳定性计算分析的最重要任务就是找到一个拥有最小安全系数的潜在滑移面。岩土科研人员在最小安全系数搜索方法上做了大量研究工作，提出了不少计算方法(陈祖煜， 2003； 陈祖煜等， 2005)。例如，陈祖煜等(1988)采用了负梯度算法，来搜寻拥有最小安全系数的潜在滑移面。Zhu(2001)计算不同位置潜在滑移面的安全系数，构造一个安全系数场来确定最小安全系数。Li et al. (2005a， 2005b)分析了天津港挖海泥航道滑坡成因机理，根据潜在滑移面空间分布来确定拥有最小安全系数的潜在滑移面，作为最有可能的滑移面。Gao(2017)，Mishra et al. (2020)采用可以避开局部最优解的非数值智算法搜寻临界潜在滑移面。

0.2 提出问题

根据包括上述文献在内的大量相关文献研究，我们发现，几乎所有进行岩土斜坡稳定性计算与分析的学者们都直接或间接地使用了一个假设：任何土质斜坡都存在一个最小安全系数，再对斜坡的潜在滑移面进行搜索，以找到这个拥有最小安全系数的潜在滑移面。然而，一般土质斜坡是否能够存在唯一最小安全系数缺乏论证。同时也缺乏对这个斜坡拥有这个最小安全系数原因的详细定量分析。另外，现有文献关于斜坡土体抗剪强度(抵抗能力)参数对斜坡稳定性分析的影响分析集中于研究抗剪强度对临界滑移面的影响(Cheng et al.，2007； Jiang et al.，2006； Li et al.，2010)，缺乏对土体黏聚力和内摩擦角分别对斜坡不同潜在滑移面安全系数作用规律的研究。

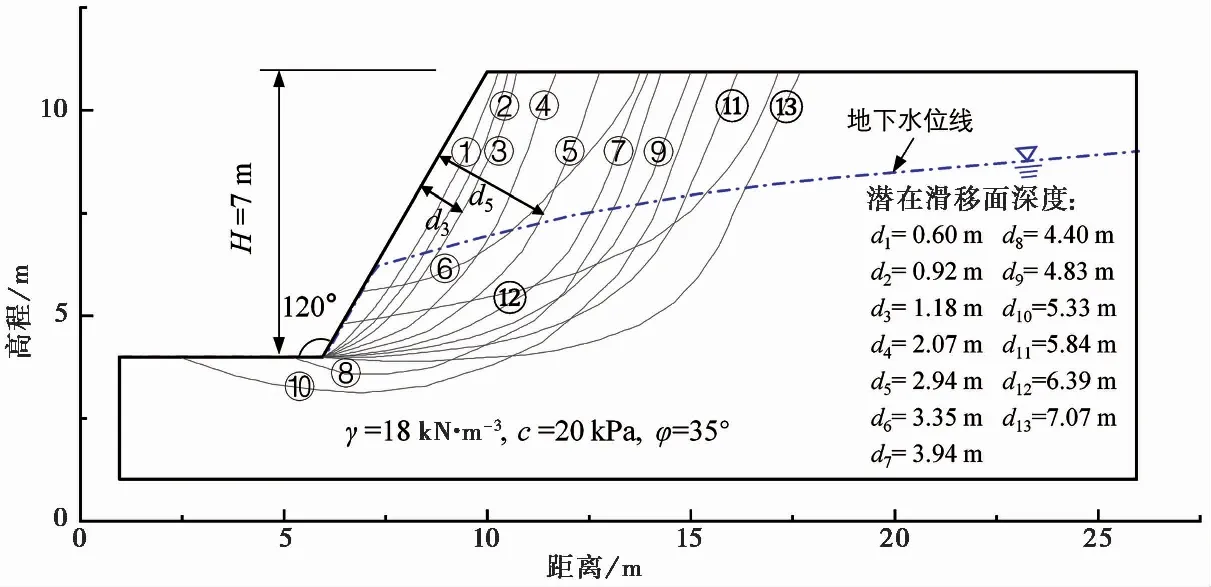
图 1 典型均质斜坡模型及不同深度的潜在滑移面Fig. 1 Typical homogeneous soil slope model and its potential slip surfaces at depths d

0.3 本文目的与方法

本文目的是论证一般土质斜坡存在唯一最小安全系数，同时，分析与给出一般土质斜坡存在唯一最小安全系数的原因。本文提出和使用的数据作图方法是，基于Slope/W商业软件，采用二维经典条分法，进行土质斜坡潜在滑移面安全系数的大量计算和作图分析。这个数据作图法展示，每个深度位置的潜在滑移面所拥有的安全系数值与深度作为一对平面坐标点。这些数据作图点可揭示，安全系数值随潜在滑移面深度的变化特征与分布规律。从而，论证一般土质斜坡存在唯一最小安全系数。本文再通过斜坡土体抗剪强度的两个参数，即土体黏聚力和内摩擦角，对斜坡安全系数的作用和贡献，来计算、分析与给出土质斜坡存在唯一最小安全系数的具体原因。为达到这两个目的，本文的内容安排如下。首先，第1节利用经典M-P条分法(Morgen-stern et al.，1965)，计算与论证一个典型均质土体斜坡存在唯一最小安全系数，并分析其原因。第2节再进一步计算、论证和分析这个斜坡在地下水作用下同样存在唯一最小安全系数和其原因。第3节计算、分析和论证5个不同经典条分法所计算出来的安全系数均存在唯一最小值和相同的存在原因。第4节计算、分析和论证分层不均质的一幅实际库岸土体斜坡也同样地存在唯一最小安全系数和原因。第5节再根据斜坡安全系数定义来进一步论证第1节到第5节中的发现与结论的正确性和根源，以及临界滑移面区间、土体含水量和控制结构面的时空因素影响与修正。最后，第6节总结了本文所发现和揭示的4条重要规律和其他重要结论。本文在使用经典M-P条分法时，均采用条间力函数为半正弦函数。

1 典型均质斜坡存在唯一最小安全系数的论证与原因

1.1 斜坡存在唯一最小安全系数的论证

1.1.1 论证方法

用于证明的这座典型均质斜坡如图 1所示。它高度为7m，倾角为60°。斜坡土体重度γ=18kN·m-3，黏聚力c=20kPa，内摩擦角φ=35°。地下水位如图 1中点划线所示。这一节论证先不考虑地下水的影响。本文选取了如图 1所示13个不同深度的潜在滑移面，它们的编号为①～。所有潜在滑移面入口在坡顶地面的不同位置处。⑥， ⑧潜在滑移面出口在坡面， ⑩和潜在滑移面出口在坡脚地面不同位置，其余潜在滑移面出口都在斜坡坡面底部端点处。定义潜在滑移面深度d为潜在滑移面与斜坡表面相平行的切面与斜坡表面之间的距离。图 1给出了这13个潜在滑移面的深度。①号潜在滑移面的深度d1=0.60m。号潜在滑移面的深度d13=7.07m。其他潜在滑移面的深度d在这两个深度之间。本节的安全系数计算均采用M-P方法。定义这一般斜坡的每个潜在滑移面所拥有的安全系数为FOSc×φ。

数据作图的论证与分析方法如图 1和图 2所示。图 2的横坐标为潜在滑移面深度d，纵坐标为潜在滑移面安全系数FOSc×φ。图 2展示了图 1的13个潜在滑移面的安全系数FOSc×φ随对应的潜在滑移面深度d的变化与特征。每个圆形散点对应于一个FOSc×φ值和它的滑移深度d。由图 2可知， ①～号潜在滑移面FOSc×φ在1.689～2.957之间。

图 2 典型均质图 1斜坡的安全系数 FOSc×φ 随对应潜在滑移面深度 d 的变化与特征(不考虑地下水)Fig. 2 Variations and features of FOSc×φ values with slip depth d for the slope model in Fig. 1(without groundwater)

每一个潜在滑移深度d可以有无数个潜在滑移面。把每个可能的相同深度d的潜在滑移面所对应的安全系数值按照它们的同一深度d在图 2坐标系中点出，可形成纵向分布的散点线。这些按照深度d的排列的散点存在一条安全系数包络线，这条曲线的极点数目和大小就确定和决定了这幅斜坡能否存在唯一的最小安全系数和对应的一条潜在滑移面。

1.1.2 论证结果

图 2所示的计算结果数据(圆形散点)初步揭示了，随潜在滑移面深度d增加，这条最小安全系数值曲线是先下降，到某一最低点(最小值)，之后再上升。这条曲线呈不对称抛物线型变化。它仅有一个极点。这个极点对应的FOSc×φ就是这幅斜坡的唯一最小安全系数值。圆形散点数据包络线的一个最小值点在深度d=2.07m(④号潜在滑移面深度d4)处，其FOSc×φ=1.689。

更进一步，这个最小值点附近，包络线较为平缓，相对应的局部最小安全系数值随深度d的变化幅度较小。为找到最小安全系数的精确结果，在该点附近再选取一个小范围的临界滑移面区间。如图 2所示，该区间是在③号潜在滑移面深度d3和⑤号潜在滑移面深度d5之间。再在该区间添加更多的密集潜在滑移面。如图 2所示，共计添加了26条潜在滑移面。图 2中十字散点展示了加密的潜在滑移面深度d和它拥有的FOSc×φ值的关系。

如图 2加密后的散点数据所示，拥有相同或相近滑移深度d的不同潜在滑移面安全系数大小不同，每个深度存在一个局部最小的安全系数，因而基于加密的散点数据更新后的安全系数包络线可定义为局部最小值包络线，斜坡总体最小FOSc×φ值和对应的深度必然在这条局部最小值包络线上，其同样为不对称抛物线型曲线。当潜在滑移面深度d从0.60增大到2.19m， FOSc×φ包络曲线单调下降。在潜在滑移面深度大于2.19m之后，FOSc×φ包络曲线又单调上升。因此，该幅斜坡仅存在唯一的最小安全系数。总体最小安全系数等于1.673，其潜在滑移面(图 2中红色滑移面)深度d为2.19m。

根据图 2中FOSc×φ和d的局部最小值包络线的不对称抛物线型变化规律，采用以下的反比例函数和线性函数的迭加公式对这条曲线进行拟合：

(1a)

式中：d为潜在滑移面深度；A、B和λc×φ为拟合系数。对于本节这幅均质斜坡，拟合后的FOSc×φ包络曲线如图 2中的红色虚线表示，具体如下：

(1b)

这条曲线函数仅存在一个最小值极点：d=2.13m和FOSc×φ=1.667。因而，论证了这幅斜坡必然仅存在唯一个总体最小安全系数。

1.2 土体黏聚力和内摩擦角对斜坡安全系数作用的不同规律

斜坡安全系数是斜坡土体抵抗下滑能力和斜坡土体重力作用下主动下滑力的比值。斜坡土体抵抗下滑能力主要体现在土体的黏聚力c和内摩擦角φ。因此，再使用数据作图法，分别计算与分析c和φ对安全系数的各自贡献规律和作用，从而探讨这个存在原因。

图 3 典型均质图 1斜坡在φ=0°条件下的安全系数 FOSc 随对应潜在滑移面深度 d 的变化与特征(不考虑地下水)Fig. 3 Variations and features of FOSc values with slip depth d for the slope in Fig. 1 at φ=0° condition(without groundwater)

1.2.1 土体黏聚力c对斜坡安全系数的作用与规律

假设图 1所示的典型均质斜坡的c=20kPa，但是φ=0°。斜坡仅有黏聚力作为抵抗下滑的能力。在这个假设条件下，斜坡的安全系数定义为FOSc。再采用1.1节中的论证方法，计算和分析这幅均质斜坡的FOSc与潜在滑移面深度d的关系。图 3展示了这些计算与分析的结果。

图 3揭示了，FOSc和d的圆形和十字散点存在局部最小值包络线。局部最小FOSc值随着潜在滑移面深度d增加，呈单调下降。初期下降速度极快，后期缓慢减小，直到平稳不变。因此，采用以下反比例函数对这条曲线进行拟合：

(2a)

式中：d为潜在滑移面深度；a和λc是拟合系数。对于本节这幅均质斜坡，拟合后的总体最小FOSc曲线如图 3中的红色虚线表示，具体如下：

(2b)

图 3和式(3)揭示了，土体黏聚力c对斜坡安全系数的作用与规律是，对深度d小的潜在滑移面FOSc作用和贡献大。随着深度d的增大，它对FOSc作用和贡献越来越小和恒定。FOSc的总体最小值所对应的潜在滑移面在深部。

1.2.2 土体内摩擦角φ对斜坡安全系数的作用与规律

再假设图 1所示的典型均质斜坡的c=0kPa，但是φ=35°。斜坡仅有内摩擦角作为抵抗下滑的能力。在这个假设条件下，斜坡的安全系数定义为FOSφ。再采用1.1节中的论证方法，计算和分析这幅均质斜坡的FOSφ与潜在滑移面深度d的关系。图 4展示了这些计算与分析的结果。

图 4揭示了，FOSφ和d的圆形和十字散点存在局部最小值包络线。局部最小FOSφ值随着潜在滑移面深度d增加，一直在单调增加。初期呈线性增大，后期呈加速增大。因此，采用以下线性函数对这条曲线进行拟合：

FOSφ=bd+λφ

(3a)

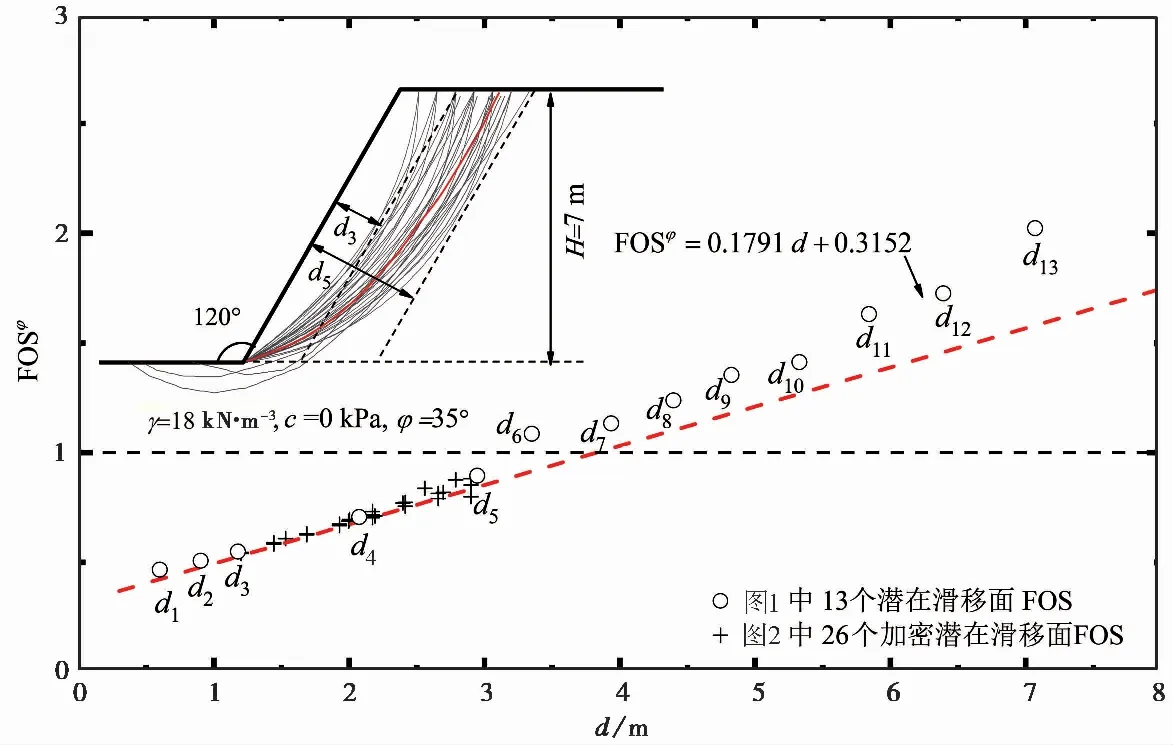
图 4 典型均质图 1斜坡在c=0 kPa条件下的安全系数 FOSφ 随对应潜在滑移面深度 d 的变化与特征(不考虑地下水)Fig. 4 Variations and features of FOSφ values with slip depth d for the slope in Fig. 1 at c=0 kPa condition(without groundwater)

式中：d为潜在滑移面深度；b和λφ是拟合系数。对于本节这幅均质斜坡，拟合后的总体最小FOSφ曲线如图 4中的红色虚线表示，具体如下：

FOSφ=0.1791d+0.3152

(3b)

图 4和式(3)揭示了，土体内摩擦角φ对斜坡安全系数的作用与规律是，对深度d大的潜在滑移面的FOSφ作用和贡献大。随着深度d的减小，它对FOSφ作用和贡献越来越小。FOSφ的总体最小值所对应的潜在滑移面在浅表面。这个结果也论证了陈祖煜(2003)的观点：“对于c=0 这样一类无黏聚土相应最小安全系数的临界滑裂面是一个非常浅的浅弧。换句话说稳定分析通常不能发现安全系数的极值，也不能发现一个具有物理意义的临界滑裂面但是发生滑坡时临界滑裂面却是客观存在的”。这个结果一致于西藏自治区林芝市波密县境内的沿帕隆藏布江展布的318国道山坡的流沙坡现象(Shang et al.， 2003)。这个结果也与无黏性土无限长斜坡的安全系数(tanφ/tanβ)一致，其中，β是无限长斜坡的坡度。

1.3 斜坡存在唯一最小安全系数的原因分析

定义由FOSc和FOSφ直接相加的共同作用安全系数FOSc+φ。它的计算公式如下：

FOSc+φ=FOSc+FOSφ

(4a)

(4b)

(4c)

式(4)揭示了，由FOSc和FOSφ直接相加获得的FOSc+φ与FOSc×φ，具有局部最小值包络线先降后升的规律。由土体黏聚力c控制的反比例降低函数和由内摩擦角φ控制的线性增大函数的迭加作用所导致的。

表 1 在图2、图3和图4所示的4类安全系数FOSc，FOSφ，FOSc×φ和 FOSc+φ随对应潜在滑移面深度d变化的数值与比值(M-P法)Table 1 Values and ratios of FOSc， FOSφ， FOSc×φ and FOSc+φ in Fig. 2，Fig. 3 and Fig. 4 vs slip depth d(M-P method)

表 1给出了图 2到图 4所示的4类安全系数FOSc，FOSφ，FOSc+φ和FOSc×φ随潜在滑移面深度d变化的数值与比值。FOSc/FOSc×φ的比值随着d的增加而减小。由在d=0.6m的比值80.80%，逐渐降低到在d=7.07m 的比值33.10%。相反地，FOSφ/FOSc×φ的比值随着d的增加而增大。由在d=0.6m 的比值16.10%，逐渐上升到在d=7.07m 的比值68.40%。FOSc+φ的值与FOSc×φ的相当一致，两者相差不大。两者的比值FOSc+φ/FOSc×φ的平均值为101.79%，最大值为104.98%，最小值为 96.08%。在最小安全系数的潜在滑移面上，FOSc+φ/FOSc×φ为98.74%。

表 1进一步揭示了，土体黏聚力c和内摩擦角φ对斜坡安全系数的贡献随深度d变化具有相反，单调且数量相当的规律，也揭示了同一潜在滑移面上的FOSc+φ与FOSc×φ值的近似相等，从而进一步论证了土体黏聚力c和内摩擦角φ均不等于0的斜坡的FOSc×φ存在唯一极小值和必定会存在唯一的最小安全系数的原因是黏聚力c和内摩擦角φ对斜坡安全系数的不同作用规律。

图 5 典型均质图 1斜坡的安全系数 FOSc×φ 随对应潜在滑移面深度 d 的变化与特征(考虑地下水)Fig. 5 Variations and features of FOSc×φ values with slip depth d for the slope in Fig. 1(with groundwater)

2 考虑地下水作用的进一步论证与原因分析

2.1 斜坡存在唯一最小安全系数的论证

第1节的论证与原因分析没有考虑地下水的作用与影响。本节再利用图 1所示的斜坡，做考虑地下水作用的进一步论证与原因分析。在斜坡安全系数计算中，地下水的作用是通过有效应力原理来获得的(陈祖煜等， 2005)。图 1所示斜坡含有一个地下水位线，可以获得静态孔隙水压强，再带入采用二维条分法公式中进行斜坡潜在滑移面所拥有的安全系数计算与分析。之后，这幅含有地下水位作用的典型均质斜坡存在唯一最小安全系数的论证与原因分析，完全依照第1节的数据作图的论证与分析方法进行。

论证计算结果如图 5中所示。图 5中的每一个十字散点表示了在地下水作用下图 1斜坡的某一个潜在滑移面的深度d值与该潜在滑移面安全系数FOSc×φ值。它们对应了图 1的13个潜在滑移面和图 5的大量加密的潜在滑移面。潜在滑移面深度d在0.6m到8m之间，FOSc×φ值在1.510～2.803之间，均大于1，处于稳定区。

图 5揭示与验证了，该幅含地下水土质斜坡每个深度d的局部最小安全系数值存在一条包络线(或最小FOSc×φ值曲线)。它也呈不对称抛物线型曲线分布。当d小于2.19m，局部最小FOSc×φ值包络线单调下降。当d大于2.19m时，局部最小FOSc×φ值包络线又单调上升。因此，该含水斜坡存在唯一的最小安全系数(FOSmin=1.510，d=2.69m)，对应于图 5中红色潜在滑移面。同样地，图 5中FOSc×φ和d的局部最小值包络线的不对称抛物线型变化规律，也可用以下的反比例函数和线性函数的迭加公式来拟合表示：

(5)

这条曲线函数仅存在一个最小值极点：d=2.30m， FOSc×φ=1.495。因此，论证和验证了含地下水作用斜坡也存在唯一最小安全系数。

对比图 2和图 5的结果可知，地下水降低斜坡FOSc×φ值，并且对深度大的潜在滑移面所拥有的FOSc×φ值降低作用大。该斜坡在有地下水和无地下水作用下的总体最小安全系数分别为：FOSmin=1.510和FOSmin=1.673。对应的潜在滑移面深度分别为：d=2.19m和d=2.69m。

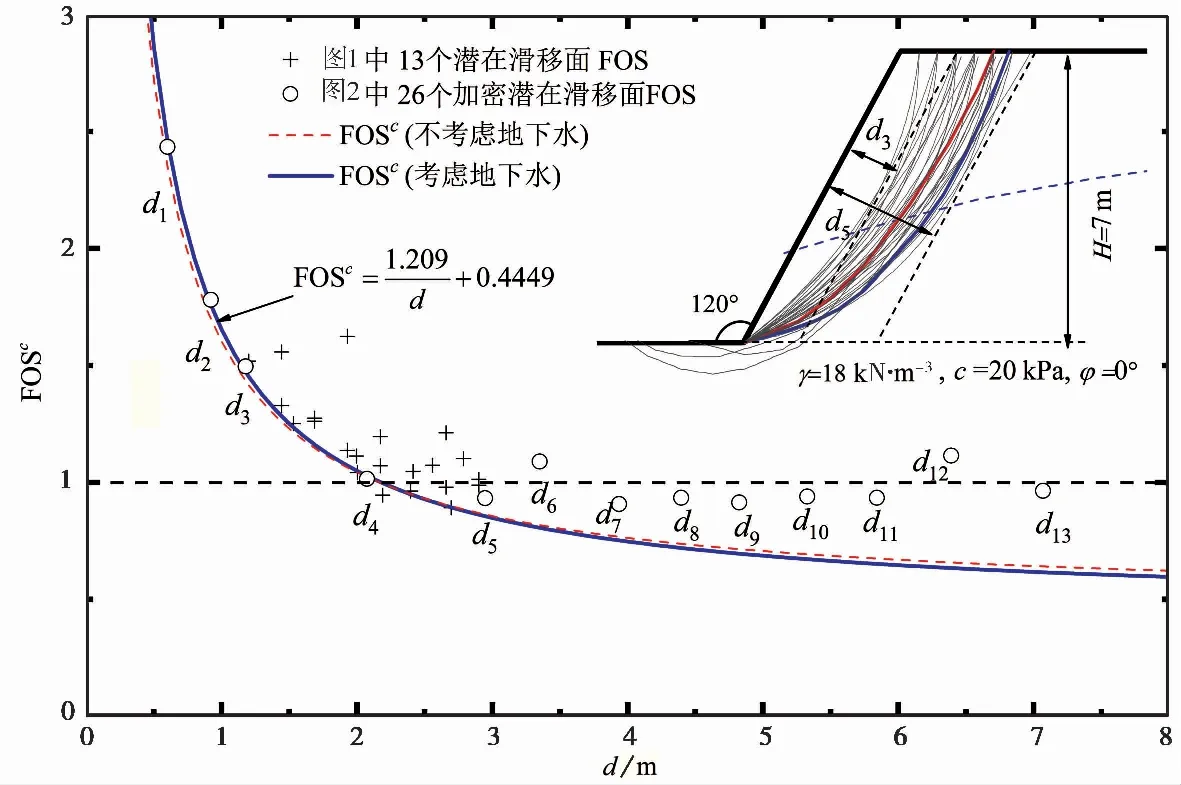
图 6 典型均质图 1斜坡在φ=0°条件下的安全系数 FOSc 随对应潜在滑移面深度 d 的变化与特征(考虑地下水)Fig. 6 Variations and features of FOSc values with slip depth d for the slope in Fig. 1 at φ=0° condition(with groundwater)

图 7 典型均质图 1斜坡在c=0kPa条件下的安全系数 FOSφ 随对应潜在滑移面深度 d 的变化与特征(考虑地下水)Fig. 7 Variations and features of FOSφ values with slip depth d for the slope in Fig. 1 at c=0 kPa condition(with groundwater)

2.2 土体黏聚力和内摩擦角对斜坡安全系数作用的不同规律

图 6、图 7给出的结果揭示了考虑地下水的影响下土体黏聚力和内摩擦角对斜坡安全系数随潜在滑在滑移面的深度变化有不同的规律。图 6揭示了，图 1含地下水斜坡在φ=0°条件下的安全系数FOSc随潜在滑移面深度d的变化与特征。对比图 3和图 6结果也揭示了，地下水对该幅斜坡的FOSc值影响极小，两条局部最小FOSc值的包络线几乎重合。如图 6十字点所示，每个潜在滑移面深度d所拥有的局部最小FOSc值随着d的增大，呈单调下降。初期下降速度极快，后期缓慢减小，直到平稳不变。因此，也可用以下反比例函数对这条包络线进行拟合：

(6)

图 7揭示了，图 1含地下水斜坡在c=0kPa条件下的安全系数FOSφ随潜在滑移面深度d的变化与特征。对比图 4和图 7结果也揭示了，图 1的地下水可较大地降低该幅斜坡的FOSφ值，降幅一般在21%。如图 7十字点所示，每个潜在滑移面深度d所拥有的局部最小FOSφ值随着d的增大，呈单调增加。初期呈线性增大，后期呈加速增大。因此，也可用以下线性函数对这条包络线进行拟合：

FOSφ=0.145d+0.256

(7)

2.3 存在唯一最小安全系数的原因分析

根据式(4a)，可再得到FOSc和FOSφ之和的FOSc+φ的数值。再根据式(6)和式(7)，可得到在地下水作用下，局部最小FOSc+φ的包络线为：

(8)

表 2具体给出了图 5到图 7所示的4类安全系数FOSc，FOSφ，FOSc+φ和FOSc×φ随深度d变化的数值与比值。FOSc/FOSc×φ(FOSc与FOSc×φ的比值)随d增加而单调减小，由d=0.6m的86.87%，降低到d=7.07m 的39.92%。相反地，FOSφ/FOSc×φ(比值)随深度d增加而单调增大，由d=0.6m的13.06%，升高到d=7.07m的61.70%。表 2也揭示了，FOSc+φ值与FOSc×φ值几乎相等。FOSc+φ/FOSc×φ的平均比值为102.65%，最大比值为106.40%，最小比值为 99.08%。在拥有最小安全系数的潜在滑移面上，FOSc+φ/FOSc×φ等于100.92%。这些定量计算结果，揭示了含地下水作用的斜坡存在唯一最小安全系数的原因。这个原因与第1.3节中给出的原因一致。

表 2 在图5、图6和图7所示的4类安全系数FOSc， FOSφ， FOSc×φ 和 FOSc+φ 随对应潜在滑移面深度 d变化的数值与比值(M-P法)Table 2 Values and ratios of FOSc， FOSφ， FOSc×φ and FOSc+φ in Fig. 5，Fig. 6 and Fig. 7 vs slip depth d(M-P method)

3 考虑不同经典条分法影响的进一步论证与原因分析

3.1 斜坡存在唯一最小安全系数的论证

第1和第2节的论证与原因分析均是基于M-P条分法计算得到的图 1斜坡多个潜在滑移面的安全系数值进行的。本节再采用其他4种基于经典条分法进行相同的论证与原因分析。它们是瑞典条分法、Janbu法、Bishop法和Spencer法。本节采用这4种经典条分法，对图 1无水均质斜坡存在唯一最小安全系数的论证与原因分析，完全依照第1节的数据作图方法进行。仅计算分析了图 1中编号为①～号的13个潜在滑移面情况。

论证计算结果如图 8所示。从图 8可见，瑞典条分法、Janbu法、Bishop法和Spencer法计算给出的斜坡安全系数FOSc×φ随潜在滑移面深度d的变化与特征，同M-P法计算给出的结果相当一致。它们的每个深度d的局部最小安全系数值均存在一条包络线(总体最小FOSc×φ曲线)。每条曲线也呈不对称抛物线型曲线分布，随d的增加先单调减小，到达总体最小值后，再单调上升。总体最小值点位于d=2.07m。瑞典条分法、Janbu法、Bishop法和Spencer法计算得到的总体最小FOSc×φ值分别为1.757、1.773、1.699和1.718。

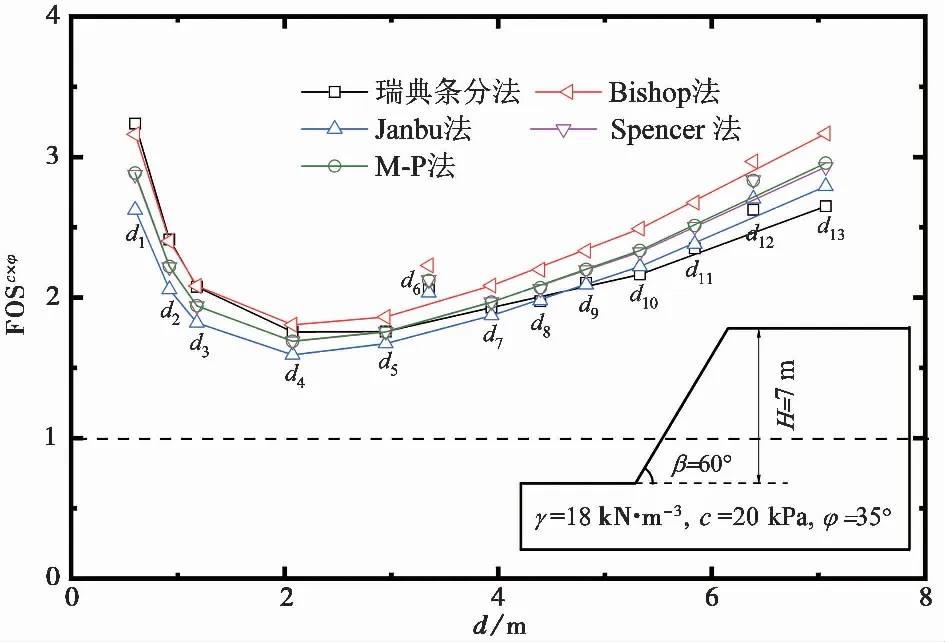
图 8 典型均质图 1斜坡经5个经典极限平衡法计算的安全系数 FOSc×φ随对应潜在滑移面深度 d 的变化与特征(不考虑地下水)Fig. 8 Variations and features of FOSc×φ values from five conventional limit equilibrium methods vs slip depth d for the slope in Fig. 1(without groundwater)

表 3 5个经典极限平衡法计算的图1所示斜坡的4类安全系数FOSc，FOSφ，FOSc×φ 和 FOSc+φ 全局最小曲线的拟合系数Table 3 Fitting coefficients of four global minimum curves of FOSc，FOSφ，FOSc×φ， and FOSc+φ from five conventional limit equilibrium methods for the slope in Fig. 1

用式(1a)的反比例函数和线性函数的迭加公式来拟合每条包络线，获得了表 3的拟合系数A，B，λslice数值。瑞典条分法、Janbu法、Bishop法和Spencer法的局部最小FOSc×φ值包络线给出的总体最小FOSc×φ值和深度d分别为：FOSc×φ=1.739，d=2.36m； FOSc×φ=1.788，d=2.10m； FOSc×φ=1.2596，d=2.02m； FOSc×φ=1.637，d=2.07m。因此，第1节的论证结果也适用于这4种经典极限平衡方法。该幅斜坡存在唯一最小安全系数值是与不同条分法本身无关。不同的条分法可能给出具体不同的最小安全系数值和不同的潜在滑移面位置，这些结果与Wan et al. (2003， 2004)给出的结果一致。

3.2 土体黏聚力和内摩擦角在不同条分法中对斜坡安全系数的作用规律

图 9 典型均质图1斜坡经5个经典极限平衡法计算的、在φ=0°条件下的安全系数 FOSc随对应潜在滑移面深度 d 的变化与特征(不考虑地下水)Fig. 9 Variations and features of FOSc values from five conven-tional limit equilibrium method vs slip depth d for the slope in Fig. 1 at φ=0° condition(without groundwater)

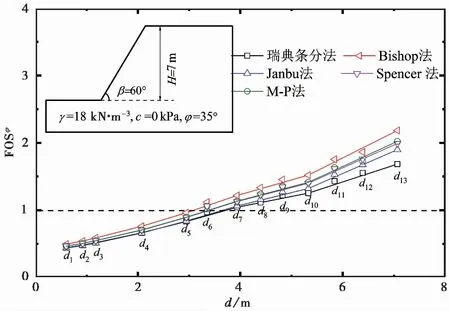
图 10 典型均质图1斜坡经5个经典极限平衡法计算的、在c=0kPa条件下的安全系数 FOSφ随对应潜在滑移面深度 d的变化与特征(不考虑地下水)Fig. 10 Variations and features of FOSφ values from five conven-tional limit equilibrium method vs slip depth d for the slope in Fig. 1 at c=0 kPa condition(without groundwater)

图 9、图 10不同经典条分法中土体黏聚力和内摩擦角对斜坡安全系数随潜在滑移面的深度变化有相反的规律。图 9揭示了，这5个经典极限平衡法计算获得的图 1斜坡在φ=0°条件下的安全系数FOSc值随潜在滑移面深度d的变化与特征。它们的每个深度d所拥有的局部最小FOSc值随深度d的增大，呈单调下降。初期下降速度极快，后期缓慢减小，直到平稳不变。因此，每条都可用式(2a)的反比例函数对这条包络线进行拟合，拟合系数a和λc数值如表 3所示。

图 10揭示了，这5个经典极限平衡法计算获得的图 1斜坡在c=0kPa条件下的安全系数FOSφ值随潜在滑移面深度d的变化与特征。每个潜在滑移面深度d所拥有的局部最小FOSφ值随着d的增大，呈单调线性增加。因此，每条包络线也可用式(3a)的线性函数对这条包络线进行拟合，拟合系数b和λφ数值如表 3所示。

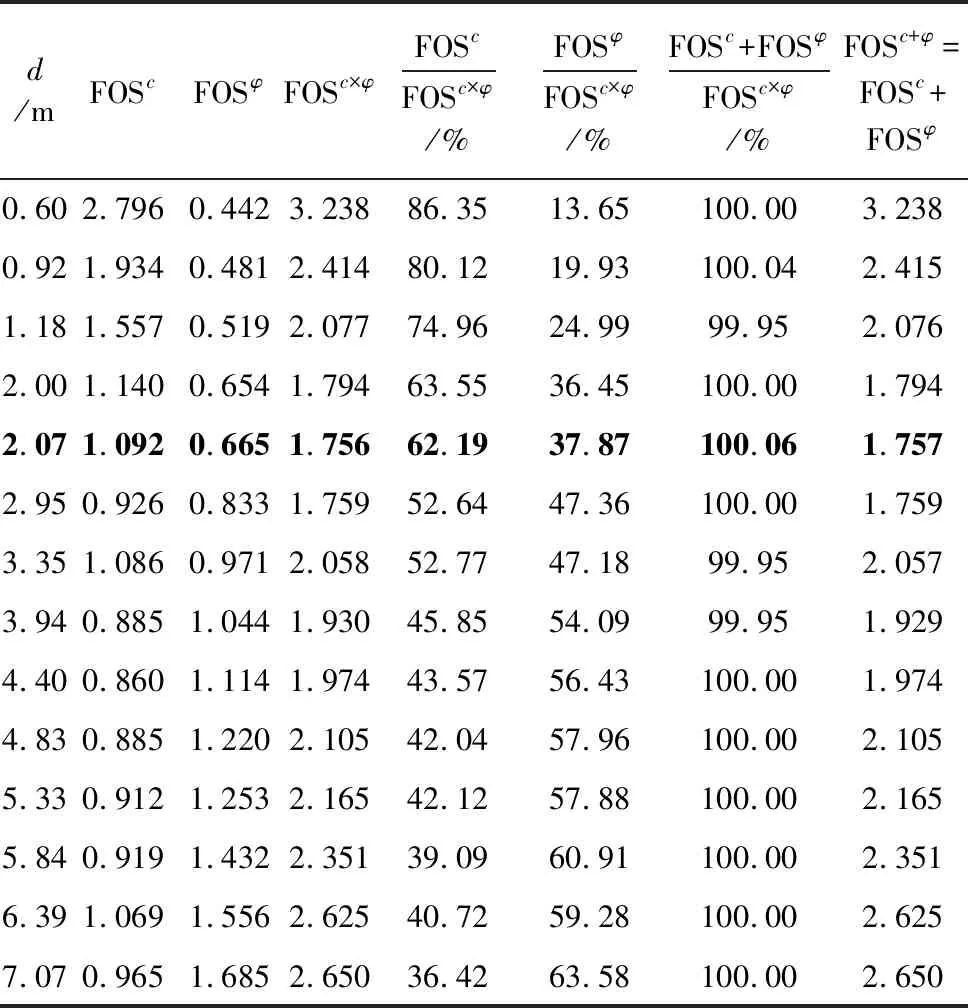
表 4 在图 8、图 9和图 10所示的4类安全系数FOSc，FOSφ，FOSc×φ和FOSc+φ随对应潜在滑移面深度d变化的数值与比值(瑞典条分法)Table 4 Values and ratios of FOSc，FOSφ，FOSc×φ and FOSc+φ in Fig. 8，Fig. 9 and Fig. 10 vs slip depth d(Ordinary method)

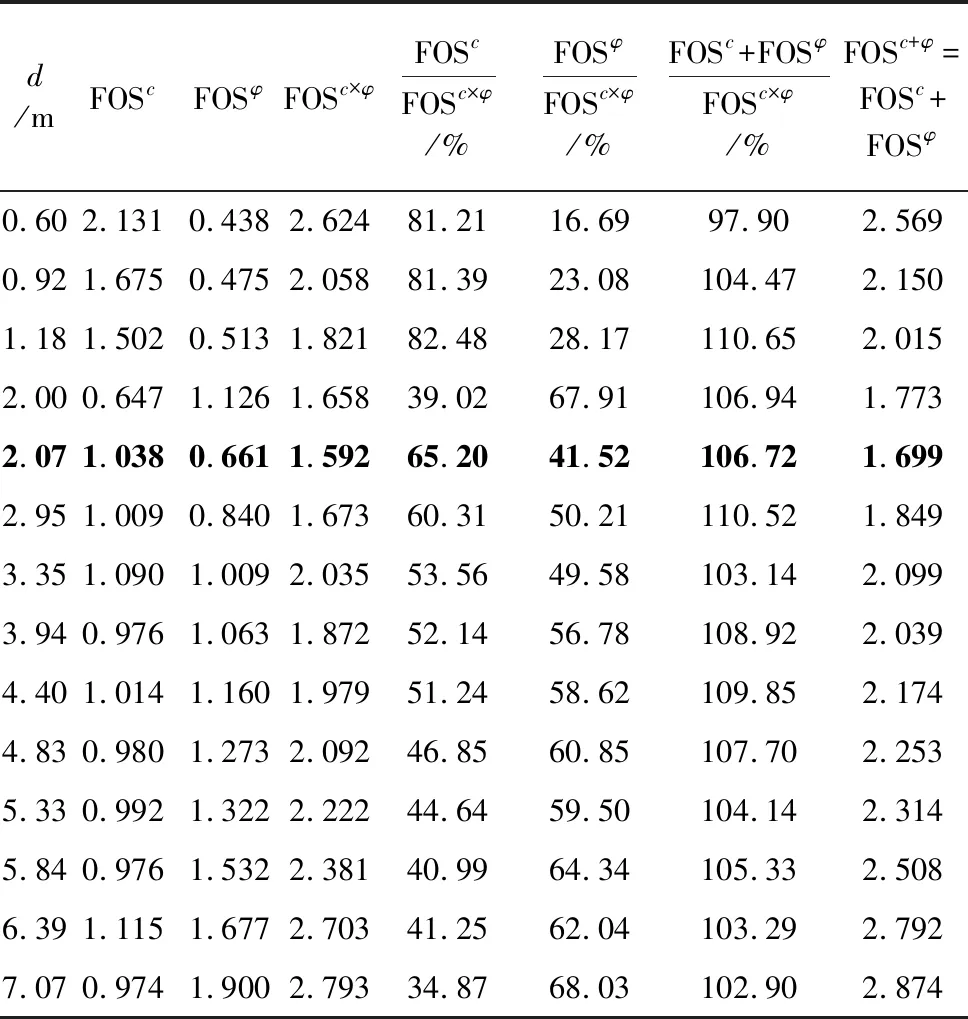
表 5 在图 8、图 9和图 10所示的4类安全系数 FOSc，FOSφ，FOSc×φ和FOSc+φ随对应潜在滑移面深度d变化的数值与比值(Janbu法)Table 5 Values and ratios of FOSc，FOSφ，FOSc×φ and FOSc+φ in Fig. 8，Fig. 9 and Fig. 10 vs slip depth d(Janbu method)

表 6 在图8、图9和图10所示的4类安全系数FOSc，FOSφ，FOSc×φ和FOSc+φ随对应潜在滑移面深度d变化的数值与比值(Bishop法)Table 6 Values and ratios of FOSc，FOSφ，FOSc×φand FOSc+φ in Fig. 8，Fig. 9 and Fig. 10 vs slip depth d(Bishop method)

表 7 在图8、图9和图10所示的4类安全系数 FOSc，FOSφ，FOSc×φ和 FOSc+φ 随对应潜在滑移面深度 d 变化的数值与比值(Spencer法)Table 7 Values and ratios of FOSc，FOSφ，FOSc×φ and FOSc+φ in Fig. 8，Fig. 9 and Fig. 10 vs slip depth d(Spencer method)

3.3 斜坡存在唯一最小安全系数的原因分析

表 4至表 7分别给出了图 8到图 10由4种条分计算方法获得的4类安全系数FOSc，FOSφ，FOSc+φ和FOSc×φ随深度d变化的数值与比值。FOSc/FOSc×φ(比值)随着d的增加而单调减小。FOSc+φ/FOSc×φ(比值)随着d的增加而单调增大。另一方面，瑞典条分法、Bishop法、Janbu法和Spencer法给出的FOSc+φ/FOSc×φ的比值，分别在99.50%到100.06%之间、96.3%到100.64%之间、97.90%到110.65%之间、96.77%到104.80%之间。

因此，第1.3节获得和揭示的土体黏聚力c和内摩擦角φ分别和共同对图 1斜坡的安全系数作用和贡献规律，与不同的经典条分法无关。斜坡存在唯一最小安全系数的原因在于土体黏聚力c和内摩擦角φ对安全系数的贡献大小随深度呈相反的减小和增大变化规律。

4 考虑斜坡分层不均质影响的进一步论证与原因分析

4.1 斜坡模型

在1985年12月4日，广西省天生桥二级电站右岸的一座山坡加人工填土的库岸斜坡发生了滑坡灾害事件。陈祖煜和邵长明利用他们在1988年提出的基于M-P条分法的最优化斜坡最小安全系数搜索方法，计算和分析了这座斜坡的最小安全系数问题(Chen et al.，1988)。如图 11所示，斜坡坡面由12段直线组成，从坡脚到坡顶3个代表性坡角分别为43.2°， 39.2°， 37.2°。坡脚到坡顶的高度为33.76m。它是由6层土体组成的分层不均质斜坡。第1层为新黏土和坡积物杂填土，第2层为老砂土、黏土和坡积物杂填土，第3层为第四纪含黏土碎石，第4层为第四纪粉细砂坡积土，第5层为第四纪淤泥黏土，第6层为第四纪砂砾坡积物。它们的抗剪强度和单位重量值在图 11中给出。底部基岩为中第三纪页岩和砂岩组成，黏聚力c=39.2kPa，内摩擦角φ=45.0°，比重2.4。实际滑坡面从被顶部新填土所埋的块石挡土墙外面开始，沿着深部近似椭球曲面一直滑到坡底。Chen et al.(1988)给出的最小安全系数值为0.8631，对应的潜在滑移面在实际滑移面上部较浅处的7条相连直线段，实际滑移面所拥有的安全系数值为0.917。

图 11 实际库岸斜坡模型(据 Chen et al.(1988)改)及不同深度局部潜在滑移面Fig. 11 Model of actual bank slope(modified after Chen et al.(1988) and its local potential slip surfaces at depths d

图 12 实际库岸图 11斜坡不同深度全局潜在滑移面Fig. 12 Global potential slip surfaces at depths d of the slope in Fig. 11

4.2 斜坡存在唯一最小安全系数的论证

本节论证采用第1节的数据作图方法，计算和分析图 11和图 12中的76条穿过不同土层、不同深度的潜在滑移面的安全系数。其中图 11中的17条局部滑移面位于斜坡上部5层土体。图 12中的65条整体滑移面穿过所有6层土体。根据计算结果，分析这些潜在滑移面所拥有的安全系数值随深度的变化规律，以论证斜坡存在唯一最小安全系数和其存在的原因。

图 13 实际库岸图 11斜坡的安全系数 FOSc×φ 随对应潜在滑移面深度 d 的变化与特征Fig. 13 Variations and features of FOSc×φ values with slip depth d for the slope model in Fig. 11

表 8 在图 13、图 14和图 15所示的4类安全系数FOSc， FOSφ，FOSc×φ和 FOSc+φ随对应潜在滑移面深度d的变化数值与比值(图11局部潜在滑移面)Table 8 Values and rations of FOSc，FOSφ，FOSc×φ and FOSc+φ in Fig. 13，Fig. 14 and Fig. 15 vs slip depth d (Local potential slip surfaces in Fig. 11)

表 9 在图 13、图 14和图 15所示的4类安全系数FOSc，FOSφ，FOSc×φ和 FOSc+φ 随对应潜在滑移面深度 d的变化数值与比值(图 12全局潜在滑移面)Table 9 Values and rations of FOSc，FOSφ，FOSc×φ and FOSc+φ in Fig. 13，Fig. 14 and Fig. 15 vs slip depth d(Global potential slip surfaces in Fig. 12)

论证计算结果如图 13、表 8和表 9所示。图 13给出了深度d在0m到13m之间的局部和总体潜在滑移面所拥有的、随深度d变化的FOSc×φ值。在深度d从6.34m到9.49m的深度区间，加密了潜在滑移面。图 13中空心倒三角点所代表图 11中局部潜在滑移面FOSc×φ值，十字散点所代表图 12中整体滑移面FOSc×φ值。可见，当深度相同时，十字散点位于空心倒三角点下方，局部潜在滑移面FOSc×φ值比整体潜在滑移面FOSc×φ值大。因此，这座斜坡发生整体滑坡的可能性大于发生局部和浅层滑坡的可能性。

图 13中空心倒三角点和十字散点的分布特征揭示了，每个潜在滑移面深度d所拥有的局部最小FOSc×φ值存在一条包络线。它在d从0m增大到8.69m区间是单调减小。当d从8.69m增大到13m区间，这条包络线再单调增大。因此，这个计算结果发现和证实了该斜坡存在唯一最小FOSc×φ值(=0.786)，对应的临界潜在滑移面如图 11和图 12中红色滑移线所示。

这条临界潜在滑移面位于Chen et al. (1988)给出的那条临界滑移面(d=10.17m)上方。本文计算的Chen et al. (1988)给出的那条临界滑移面(图 11中绿色滑移面)所拥有的安全系数值为0.837，比Chen et al. (1988)的最小值0.8631小3.0%。该斜坡实际滑坡发生的滑移面如图 11和图 12中蓝色滑移线所示，其深度d=11.40m，本文计算的该实际滑移面安全系数值为0.875，比Chen et al. (1988)的0.917小4.6%。这些计算差别应该是M-P条分法不同条间力函数假设和不同垂直细长土条划分所导致的。

根据图 13中FOSc×φ和d的局部最小值包络线的不对称抛物线型变化规律，也可用式(1a)的反比例函数和线性函数的迭加公式来拟合：

(9)

4.3 土体黏聚力和内摩擦角对不均匀斜坡安全系数的作用规律

图 14揭示了局部和整体潜在滑移面所拥有的FOSc值随深度d的变化与特征。图 14空心倒三角点和十字散点揭示了，局部潜在滑移面所拥有的FOSφ值与整体潜在滑移面所拥有的FOSφ值相差不大。随着d从0m增大到13m，每个潜在滑移面深度d的局部最小FOSc值从2.241单调地降低到0.352。初期降低速度快，后来变缓慢。因此，可用式(2a)拟合这条包络线：

(10)

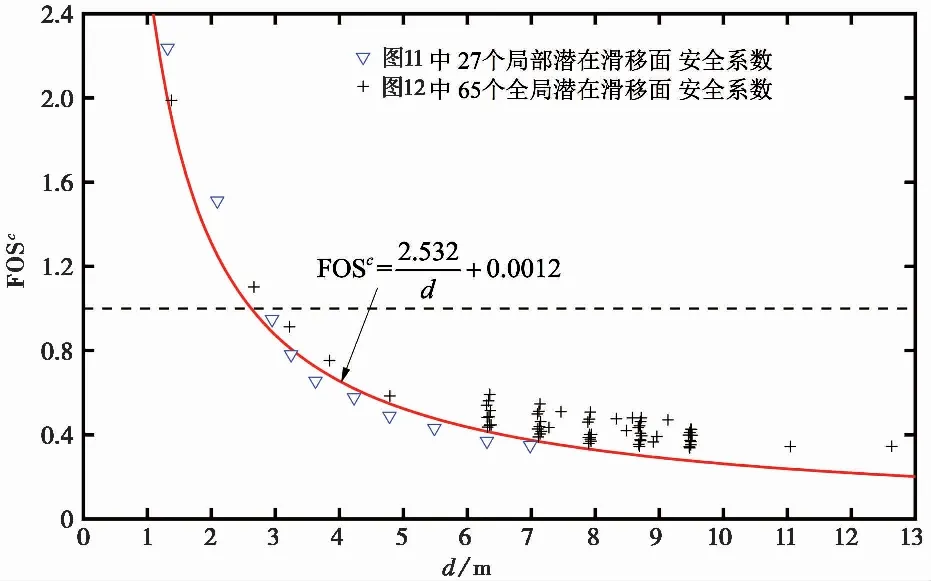
图 14 实际库岸图 11斜坡在φ=0°条件下的安全系数 FOSc随对应潜在滑移面深度 d 的变化与特征Fig. 14 Variations and features of FOSc values with slip depth d for the slope in Fig. 11 at φ=0° condition

图 15揭示了局部和整体潜在滑移面所拥有的FOSφ值随深度d的变化与特征。图 15空心倒三角点和十字散点揭示了，局部潜在滑移面所拥有的FOSφ值比整体潜在滑移面所拥有的FOSφ值大很多。随着d从0m增大到13m，每个潜在滑移面深度d的局部最小FOSφ从0.444几乎线性地增大到0.581。因此，也可采用式(3a)对FOSφ～d包络点进行拟合，得到这条FOSφ包络线：

FOSφ=0.0395d+0.079

(11)

图 15 实际库岸图 11斜坡在c=0 kPa条件下的安全系数FOSφ随对应潜在滑移面深度 d 的变化与特征Fig. 15 Variations and features of FOSφ values with slip depth d for the slope in Fig. 11 at c=0 kPa condition

4.4 存在唯一最小安全系数的原因分析

式(10)和式(11)之和给出了FOSc+φ的包络线方程：

(12)

由式(9)和式(12)可知，FOSc×φ和FOSc+φ的两条包络线，随着潜在滑移面深度d的变化规律一致。

表 8和表 9分别进一步给出了局部和整体潜在滑移面所用的4类安全系数值和它们的比值随d的变化。表 9揭示了，FOSc/FOSc×φ(比值)，随着d增加而不断减小，由d=0.8m 的89.43%，降低至d=12.63m 的39.15%。FOSφ/FOSc×φ(比值)，随着d增加而不断增大，由d=0.8m的10.18%，升高至d=12.63m 的64.63%。同时，FOSc+φ/FOSc×φ的平均比值为100.24%，最大比值为103.78%，最小比值为 98.80%，最小安全系数滑移面的FOSc+φ/FOSc×φ比值为100.25%。同一潜在滑移面的FOSc+φ数值约等于FOSc×φ。因此，FOSc+φ与FOSc×φ的比值相当或相等。这些定量计算结果，揭示了含多层不均质斜坡存在唯一最小安全系数的原因是与第1.3节中给出的原因一致。

5 进一步的论证、分析与讨论

5.1 基于安全系数基本定义的论证与原因

基于土体莫尔-库仑抗剪强度准则和太沙基孔隙水有效应力原理，斜坡安全系数定义如下(陈祖煜， 2003)：

(13)

式中：c′ 为土体有效黏聚力；φ′ 为土体有效内摩擦角；σ′n、τn和u分别为潜在滑移面上的总正应力、剪切应力和孔隙水压强。

如果再定义，仅由土体黏聚力贡献和仅由内摩擦角贡献的斜坡安全系数分别为FOSc和FOSφ。根据式(13)，它们可表示为：

(14)

(15)

因此，上述4类安全系数有以下关系：

FOSc+φ=FOSc+FOSφ

(16)

在定义式(13)～式(16)中，相对于一座给定的斜坡，c′ 和φ′ 值是常数，σ′n、τn、u和(σ′n-u)/τn一般均随潜在滑移面深度d的增大而增大。因此，可以有以下变化规律与特征。1)FOSc随d增大而单调减小； 2)FOSφ随d增大而单调增大； 3)FOSc×φ随d增大先单调减小、再单调增大； 4)FOSc一般不随u变化； 5)FOSφ随u增大而单调减小； 6)FOSc×φ随u增大而单调减小； 7)FOSc×φ=或≈FOSc+φ。这些变化特征和规律是与第1到第4节所论证的特征和规律相一致，它们共同使得斜坡安全系数存在唯一最小值。

5.2 唯一最小安全系数滑移面的不唯一性：最小安全系数的潜在滑移面区间

上述数据作图法也揭示了，最小安全系数对应的潜在滑移面附近还存在大量的潜在滑移面，它们的安全系数值仅略高于最小值。将深度d的局部最小安全系数与总体最小安全系数相差在5%内的深度区间定义为最小安全系数滑移面区间。由图 2可知，图 1的典型均质斜坡最小安全系数为1.673，对应潜在滑移面深度d为2.19m。但是，在深度d位于2.00m到2.95m之间条件下，每个深度d所对应的大量潜在滑移面的局部最小安全系数值在1.673～1.756之间，与总体最小安全系数相差在0～4.96%之间。因此，在临界潜在滑移面深度d附近的2.00m到2.95m之间，存在一系列潜在滑移面，它们的安全系数值近乎等于或略大于这个所谓的最小安全系数值。

图 5揭示了，图 1的典型均质斜坡在地下水作用下的最小安全系数值为1.510，对应的临界潜在滑移面深度为2.69m。但是，在深度d位于2.40m到2.95m之间条件下，每个深度d所对应的大量潜在滑移面的局部最小安全系数值在1.510～1.580之间，与总体最小安全系数相差在0～4.64%之间。因此，在临界潜在滑移面深度d附近的2.40m到2.95m之间时，存在一系列潜在滑移面，它们的安全系数值近乎等于或略大于这个所谓的最小安全系数值。

图 13进一步揭示了，图 11的分层不均质斜坡最小安全系数为0.786，对应滑移面深度为8.69m。但是，在深度d位于7.13m到9.49m之间条件下，每个深度d所对应的大量潜在滑移面的局部最小安全系数值在0.786～0.823之间，与总体最小安全系数相差在0～2.80%之间。因此，在临界潜在滑移面深度d附近的7.13m到11.40m之间，存在一系列潜在滑移面，它们的安全系数值近乎等于或略大于这个所谓的最小安全系数值。

本文数据作图法的结果揭示和论证了，一般斜坡存在唯一最小安全系数FOSc×φ值和对应的一条临界潜在滑移面。但是，在这条临界潜在滑移面附近存在大量其他潜在滑移面，它们各自的安全系数FOSc×φ值几乎等于或略高于这个最小安全系数值。特别地，不少拥有略大于这个最小安全系数值的潜在滑移面位于更深处，拥有更多可下滑的土体体积和重量，更具下滑破坏能力。因此，最深处拥有略大于这个最小安全系数值的潜在滑移面，从安全角度考虑，应该最为重要。这个结果也就揭示和解释了，图 11所示的实际滑坡面位置(d=11.40m)深度大于Chen et al. (1988)和本文给出的两条临界滑移面位置(d=10.18m和d=8.69m)。本文统一计算的这3条潜在滑移面所拥有的安全系数值分别为0.875、0.837和0.786。潜在滑移面深度越大，滑移面上方土体体积越大，成为实际滑坡面的可能性和危害性也更大。

因此，所谓的唯一最小安全系数和其所对应的临界潜在滑移面的概念应该主要是数学计算上的概念。这可能导致了，人们建立的多种最小安全系数值搜索算法的结果总是存在一些差异。最为重要的是，这些算法得到的最小安全系数值可能仅有微小的差异，但是，它们搜索到的临界潜在滑移面深度位置可能相差较大。本文从图 2、图 5和图 13给出的局部最小安全系数值包络线方法，揭示和给出了这些与最小安全系数值几乎相等的大量潜在滑移面位置区间，这个结果可以更好地确定和选择最具实际危险的潜在滑移面，进行斜坡稳定安全性评价和滑坡防治设计。例如，Wan et al. (2003，2004)年发现和揭示了，在土钉加固潜在不稳定斜坡的设计计算中，需要设防的潜在滑移面比拥有最小安全系数的潜在滑移面更深，需要从土钉获得更大抗滑阻力，以达到同样的安全系数设计标准值(1.4)。

5.3 土体黏聚力和内摩擦角随时间和含水量的变化与作用

应该指出，以上论证与认识是，基于太沙基土体孔隙水有效应力原理，假设土体黏聚力c和内摩擦角φ值(或有效黏聚力c′和有效内摩擦角φ′值)是常数的条件下获得的。根据岳中琦等(2013)和岳中琦(2015)的研究结果，土体黏聚力(c或c′)和内摩擦角(φ或φ′)值在时间上不是常数，它们随土体孔隙含水量的增大而逐渐、快速减小。它们随时间和含水量增大而减小使得斜坡抗下滑能力大大降低，是发生滑坡的最根本原因之一。本文结果进一步揭示了，在土体黏聚力c和内摩擦角φ值下降到某种临界值时，原来稳定的斜坡要发生滑坡的规律。这个规律就是，一座斜坡在理论上存在唯一的最小安全系数和对应的临界潜在滑移面。同时，在这个理论临界滑移面附近存在大量其他潜在滑移面，它们拥有的安全系数值仅仅略大于这个最小安全系数值。因此，真正发生滑坡的潜在滑移面可能比这个理论临界潜在滑移面位于较深的位置。

5.4 斜坡土体内结构面的控制作用

本文上述论证和分析是基于斜坡不存在黏聚力或内摩擦角极小的控制性软弱或光滑结构面。如果土体中存在控制性结构面，那么，该斜坡的拥有最小安全系数的临界滑移面可能沿着这条控制性结构面发展。这个控制性结构面可能是断层面和地层界面(王思敬， 1997；Yue et al.， 2002)。

特别地，图 11所示的库岸斜坡，它的顶部滑坡面是沿着填土和挡土墙之间的接触面，下部滑移面是沿着第四纪坡积土石体与基岩的接触面。因此，这个滑坡可能是由这两个结构接触面控制的。特别地，如果最顶部新填土与墙面接触面的黏聚力和内摩擦角值小于这层新填土的黏聚力和内摩擦角值，那么，这个土-墙接触面就能成为一条软弱或光滑控制性结构面。它会导致沿土墙接触面发展的潜在滑移面的安全系数值降低。这会使得从这个算例的实际滑坡面的安全系数值0.875降低到相当于上述临界滑移面拥有的最小安全系数值0.786。因此，由结构面控制的斜坡会有另外一类滑坡模式。这需要进一步、具体地研究这种条件对本文所论证和揭示规律的影响。

6 结 论

本文提出了为什么一般土质斜坡存在唯一最小安全系数和唯一最小安全系数存在的原因是什么的问题。为解决这两个基本问题，本文定义了每一潜在滑移面所拥有的4类安全系数FOSc×φ、FOSc、FOSφ和FOSc+φ。采用经典极限平衡原理的有限条分算法，计算了斜坡大量不同深度d潜在滑移面的安全系数，并用数据作图法进行论证和分析，研究了黏聚力和内摩擦角对斜坡安全系数的分开和共同作用随潜在滑移面深度d变化的规律。FOSc×φ、FOSc、FOSφ和FOSc+φ随潜在滑移面深度d变化有以下4条特征和规律。

(1)FOSc×φ由土体黏聚力和内摩擦角贡献的安全系数。计算结果揭示了，它在每个潜在滑移面深度d的局部最小值随d的增加先单调减小，到达一段最小值区间后，再单调增大，呈不对称抛物线型变化，局部最小值包络线可用反比例函数和线性函数的迭加公式拟合。因此，它必然存在一个总体最小值，而一般土体斜坡总是在有限深度存在一条拥有唯一最小安全系数的潜在滑移面。

(2)FOSc仅由土体黏聚力贡献的安全系数。计算结果揭示了，它在每个潜在滑移面深度d的局部最小值随d的增加先快速、再缓慢单调减小，局部最小值包络线可用反比例函数公式拟合。从而，内摩擦角等于0的纯黏土斜坡总是在深处存在多条拥有唯一最小安全系数的潜在滑移面。

(3)FOSφ仅由土体内摩擦角贡献的另外一部分安全系数。计算结果揭示了，它在每个潜在滑移面深度d的局部最小值随d的增加线性减小，局部最小值包络线可用线性函数公式拟合。从而，黏聚力等于0的纯砂土斜坡总是以坡表面做为唯一最小安全系数的潜在滑移面。

(4)FOSc+φ等于FOSc+FOSφ。计算结果揭示了，FOSc+φ数值几乎等同于FOSc×φ数值，也有相同的随d的变化特征与规律。因此，更进一步揭示了，经典有限条分计算方法在土体黏聚力和内摩擦角对斜坡安全系数FOSc×φ的耦合作用和贡献极其有限。

上述4条特征和规律论证了土质斜坡安全系数存在唯一最小值，揭示了土体内摩擦角和黏聚力对斜坡安全系数的作用随深度变化的不同规律，从而给出了土质斜坡安全系数存在唯一最小值。

基于有效应力原理，考虑地下孔隙水压强作用的计算结果揭示了，上述(1)到(4)条特征和规律是适用于地下孔隙水压强作用的结果。地下孔隙水压强可有效地降低FOSc×φ值和FOSφ值，对FOSc值的影响极其有限，同时地下水会加深拥有最小安全系数的潜在滑移面的深度。基于5种经典有限条分计算方法的结果揭示了，上述(1)到(4)条特征和规律适用于不同条分计算方法的结果。基于考虑斜坡土体分层不均质的计算结果揭示了，上述(1)到(4)条特征和规律适用于斜坡土体分层不均质斜坡的结果。

本文给出的数据作图结果也揭示了唯一最小安全系数FOSc×φ值对应的潜在滑移面附近存在大量安全系数FOSc×φ值与最小安全系数值相差极少的其他潜在滑移面。特别地，不少拥有略大于这个最小安全系数值的潜在滑移面位于更深处，拥有更多可下滑的土体体积和重量，更具下滑破坏能力。本文给出的安全系数值包络线方法，揭示和给出了这些与最小安全系数值几乎相等的大量潜在滑移面位置区间，这个结果可以更好地确定和选择最具实际危险的潜在滑移面，进行斜坡稳定安全性评价和滑坡防治设计。

本文指出了，土体黏聚力(c或c′)和内摩擦角(φ或φ′)值在时间上不是常数，它们随土体孔隙含水量的增大而逐渐、快速减小。在土体黏聚力和/或内摩擦角值下降到某种临界值时，原来稳定的斜坡要发生滑坡。这是原来稳定斜坡再发生滑坡的最根本原因之一。另外，如果斜坡土体中存在控制性(黏聚力或内摩擦角极小)软弱或光滑结构面，那么，需要进一步、具体地研究这种条件对本文所论证和揭示规律的影响。

致 谢岳中琦感谢2017年全国工程地质学术年会组委会的邀请在大会上做了题目为《土体内摩擦角和黏聚力对斜坡安全系数作用的同异规律》特邀报告、2013年第四届全国岩土与工程学术大会组委会的邀请在大会上做了题目为《岩土工程行业发展的技术性思考》特邀报告和2013年第六届全国地质灾害与防治学术会组委会的邀请在大会上做了题目为《现今滑坡灾难防治的两个本质性错误》特邀报告。康兴宇感谢香港大学的博士生奖学金资助。