基于频陷特征的薄层砂地比预测方法及应用——以阿尔及利亚X区块为例

袁野，韩文明，赵红岩，刘琼，陈全红

中国海洋石油国际有限公司海外技术支持中心，北京 100028

阿尔及利亚X区块地表被沙漠覆盖，主要目的层埋深近4000m，上覆巨厚膏、岩盐，导致深层地震资料高频成分缺失，地震主频较低仅有18Hz，可以分辨的地层厚度约为60m。同时研究区目的层上覆火成岩，通过已钻井合成地震记录标定显示，在低分辨资料背景下，目标砂岩储层的地震反射特征完全淹没在火成岩与下覆大套泥岩间的强波阻抗界面之内(见图1)，导致地震储层预测难度较大，常规地震储层预测方法效果不佳。

图1 合成地震记录标定图Fig.1 Calibration diagram of synthetic seismic records

针对低分辨率地震强屏蔽下的薄储层预测这一难题，目前国内外研究主要集中在时域分析和频域分析2个方向。时域分析主要从地震资料中提取振幅类信息，以调谐振幅作为研究的主要手段：文献[1，2]运用薄层模型分析振幅与厚度间的关系预测薄层厚度，但主要基于模型进行研究，未开展实际资料应用；文献[3]基于90°相位剖面运用调谐振幅预测薄层厚度，但90°相位技术对单砂体厚度有一定要求，在此次研究区不适用；文献[4]开展了处理解释一体化的调谐振幅分析研究，但处理解释一体化的组织方式在海外区块难以实践。频域分析主要运用小时窗对地震资料进行谱分解，聚焦薄层所在地震反射同相轴上下的频率特征[5]：文献[6,7]分析了峰值频率与薄层间的关系；文献[8]分析了薄层瞬时频谱的峰值频率和陷频频率特征；文献[9]运用谱反演方法识别薄层，但相关研究主要基于模型数据，未开展实际资料应用；文献[10]运用分频方法开展薄层储层预测，但也指出分频方法受地震资料信噪比影响较大，纵向分辨率也有极限；文献[11]运用谱分解方法预估薄层厚度，但也指出研究主要针对大套泥岩中的薄砂岩预测，对此次研究靶区的“砂包泥”岩性组合是否适用也需要开展进一步分析。

通过调研分析，笔者发现频率信息对薄层顶底的反射系数不敏感，对厚度更敏感，在对储层砂地比的预测中，频域方法相比时域方法多解性更低，稳定性更好。为此，在前人研究基础上，通过分析薄储层的调谐效应在频率域引发的能量谱变化特征，利用模型试算提出了利用第一频陷处能量属性表征砂地比的思路；在研究区基于实际资料开展属性的提取和应用，已钻井显示提取的属性与目的层段砂地比具有较好的相关性；相关研究为储层“甜点”预测和评价井部署提供支撑，并得到了新钻井R-1井的验证。

1 方法原理

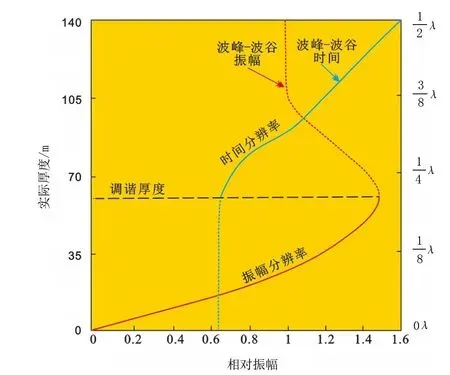
图2 振幅和时间分辨率与地层厚度变化示意图Fig.2 Schematic diagram of amplitude and time resolution and formation thickness variation

在频率域，薄层调谐效应表现为薄层顶底反射相互干涉导致的周期性频陷现象[13]。假定某一薄层顶底界面的反射系数分别为r1和r2，透射系数分别为t1和t2，通过薄互层的地震波为f(t)，其对应频谱为g(jω)，薄层顶底界面的双程旅行时为τ，则当地震波通过薄层后，在地面接收到的地震反射波为顶底反射波的叠加，可以表示为：

r(t)=r1f(t)+t1r2t2f(t+τ)

(1)

对应的频谱表示为：

r(jω)=(r1+t1r2t2e-jωτ)g(jω)

(2)

薄层可以认为是一个滤波器，改变了入射地震波的频谱特性，它的频谱特征k(jω)可以表示为：

k(jω)=r1+t1r2t2e-jωτ=r1+t1r2t2cosωτ-jt1r2t2sinωτ

(3)

假设地震波垂直入射，反射系数极小，透射系数接近于1，此时薄层的滤波频谱特征可以简化为：

k(jω)=r1+r2cosωτ-jr2sinωτ

(4)

此基础上，再假设薄层顶底界面的反射系数大小相等，正负相反，如厚泥岩中夹薄砂或厚砂中夹薄泥时，则有r1=r，r2=-r，此时的薄层滤波频谱特征可以表示为：

k(jω)=r(1-cosωτ+jsinωτ)

(5)

对应的振幅谱为：

(6)

对应的能量谱为：

|k(jω)|2=2-2cosωτ

(7)

可以看到，薄层的能量谱为一周期函数，当ωτ=2n-π，n=1,…,N，N→∞时，能量谱达到极值，出现陷频现象。第n个陷频为：

(8)

相邻2个陷频的频率之差为：

(9)

理论上看，这种频陷特征与薄层的厚度有密切关系。通过式(7)可以看到，在第1个频陷处，地震反射的能量谱和薄层的厚度呈反比关系。因此通过对薄地震反射频率特征的分析，可以预测薄储层厚度的分布。

2 频陷特征正演与属性构建

为探讨薄层能量谱与厚度间的关系，基于研究区“砂包泥”的岩性组合特征，通过设计薄层楔形模型以开展正演分析。根据已钻井揭示的地层岩性组合和厚度变化特征，在大套海相低速泥岩(Layer1，Layer6)内设置了多套自上而下依次为45m火成岩(Layer2)、5m泥岩(Layer3)、35 m砂岩(Layer4)和0～15m楔形薄泥岩(Layer5)的地质模型(见图3(a))。各层模型岩性参数和厚度取值如表1所示，采用16Hz负极性雷克子波进行自激自收正演模拟，时间域正演地震道如图3(b)所示。

表1 正演模型参数取值

图3 正演模型与剖面图Fig.3 The diagrams of forward modelling and profile

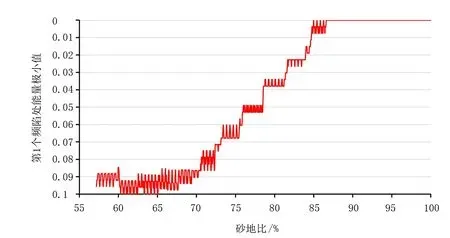
图4 正演模型第1个频陷处能量极小值与砂地比交会图Fig.4 Crossplot of energy minimum at the first frequency notch and sand ratio of forward modelling

对比地质模型，正演地震道中低频强波谷(蓝色反射同相轴)为火成岩顶面反射界面，低频强波峰(红色反射同相轴)为砂岩底面反射界面。为进一步分析砂岩中薄层楔形泥岩的频率特征，以上述强波谷和波峰反射峰值为时窗上下界对地震道进行谱分解。在频率域，可以看到在地震主频16Hz处出现能量谱峰值，而随着频率的增大，在约53Hz处出现了第1个频陷，在约80Hz处出现了第2个能量谱峰值(见图3(c))。这也与式(9)和表1中的参数计算得到的频率变化周期相符合(周期Δf=1/(35/4500×2)≈64，与图3(c)中2个能量谱峰值间频率差一致)。在第1个频陷处沿该频陷以小时窗提取了能量谱极小值，并与正演模型中Layer4和Layer5代表的砂岩储层段的砂地比进行交会分析，结果显示两者呈反比关系(见图4)。

3 应用

阿尔及利亚X区块的主力储层为三叠系河流相砂岩，其埋藏深度深(大于3500m)，成岩作用强，储层厚度薄(30～50m)，砂地比高(40%～90%)，呈典型“砂包泥”特征[14]。已钻井揭示该套储层厚度横向变化大，储层物性主要受成岩作用影响，在河道叠置关系较好的主体区，砂地比较高，储层物性普遍较好(见图5)。因此，开展研究区储层砂地比预测能直接指示储层“甜点”的分布特征，对探井和评价井的部署具有重要意义。

图5 研究区已钻井孔隙度与砂地比交会图 Fig.5 Crossplot between sand ratio and porosity for drilled wells in the study area

以该区三维叠前时间偏移地震资料为基础，沿目的层之上和之下地震反射同相轴为时窗顶底进行谱分解，得到频率域剖面(见图6)，剖面位置见图7。在频率域剖面上可以观察到第1个频陷，提取该频陷处的能量谱极小值，得到了第1个频陷处能量极小值属性(见图7)。将已钻井处属性值与储层砂地比进行交会分析，可以看到两者呈反比关系，与正演楔形模型的特征保持一致(见图8)。以70%砂地比对应的第1个频陷处能量极小值属性为阈值，在属性平面上表征研究区相对高砂地比的河道主体区。

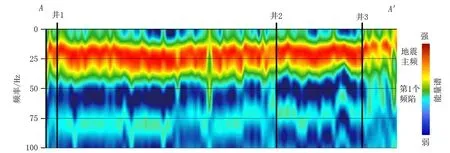
图6 实际三维地震目的层段频率域剖面Fig.6 Frequency domain profile of actual 3D seismic target layer

图7 第1个频陷处能量极小值属性图Fig.7 Energy minimum attribute graph at the first frequency notch

图8 已钻井第1个频陷处能量极小值与砂地比交会图Fig.8 Crossplot between the energy minimum at the first frequency notch and sand ratio of drilled wells

基于属性分析结果，研究区东南部河道主体为南东-北西向展布，西南部河道主体为近南-北向展布，指示了2支不同方向的物源(见图7)。在2支物源交会处的R-1井储层段砂地比达到75%，钻遇油层18m，渗透率可达235mD，DST测试日产轻质油超过千方，均创下了研究区新高。

4 结论

运用正演模型分析了薄储层在频率

域的调谐效应特征，基于频陷特征构建了第1个频陷处能量极小值属性，并在实际资料进行应用，取得较好应用效果。

1)厚层地层中的薄层在地震资料的频率域会出现周期性的频陷特征，频陷出现的周期与薄层厚度有关。

2)基于理论分析和正演模型验证，在第1个频陷处地震反射的能量谱和薄层的厚度呈反比关系。利用第1个频陷处的能量极小值属性可以一定程度上表征薄砂岩层段的砂地比。

3)该方法具有较好的可操作性，在实际资料应用中取得较好效果，具有一定的推广应用价值。