高三一轮复习检测题(选修3—1、3—2)B卷参考答案与提示

1.B 提示:假设质点由Q点向P点运动,作出轨迹上某点的速度和静电力,如图1所示。因为静电力和速度的夹角为钝角,所以静电力做负功,电势能增大,动能减小,选项B 正确,C 错误。因为带负电的质点在P点时的电势能较大,所以P点电势较低,即三个等势面中,c的电势最低,选项A 错误。因为P点的电场线比Q点的密集,所以质点在P点受到的静电力较大,产生的加速度较大,选项D错误。假设质点由P点向Q点运动,可得出同样的结论。

2.D

3.A 提示:当I1=I2=I3时,令B1=B2=B3=B0,根据安培定则画出I1、I2、I3在O点产生的磁感应强度示意图,如图2甲所示,根据矢量叠加原理可知,此时O点的磁感应强度大小B与B0满足关系式。当I1=3I,I2=I3=I时,B1=3B0,B2=B3=B0,同理作出O点的磁感应强度示意图,如图2乙所示,则O点的磁感应强度大小为4B0=2B,选项A 正确,B 错误。当I2=3I,I1=I3=I时,B1=B3=B0,B2=3B0,则O点的磁感应强度示意图如图2 丙所示,O点的磁感应强度大小为,同理可得,当I3=3I,I1=I2=I时,O点的磁感应强度大小也为,选项C、D 错误。

4.B 提示:粒子在加速电场中运动时,根据动能定理得,粒子在磁场中做匀速圆周运动,根据洛伦兹力提供向心力得,解得。因此质子和α粒子分别在磁场中偏转时,磁场的磁感应强度之比,即需将磁场的磁感应强度大小变为2B。

5.C 提示:题图所示位置线圈与磁场方向平行,穿过线圈的磁通量为零,选项A 错误。线圈绕转轴OO′转动的角速度ω=2πn,线圈转动产生的感应电动势的最大值Emax=NBSω=NBL2·2πn=2πNBL2n,选项B 错误。交流发电机产生的感应电动势的有效值,则电流表的示数,电压表的示数U=,选项C正确,D 错误。

6.C 提示:线框bc边的位置坐标x由L到2L的过程中,线框bc边的有效切割长度l=x-L,产生的感应电动势E=Blv=B(x-L)v,感应电流电流逐渐增大;根据楞次定律可以判断出感应电流的方向为abcda,为正值。线框bc边的位置坐标x由2L到3L的过程中,根据楞次定律可以判断出感应电流的方向为adcba,为负值;线框ad边的有效切割长度l=x-2L,产生的感应电动势E=Blv=B(x-2L)v,感应电流,电流的大小逐渐增大。

7.AD 提示:电子在静电场中运动,根据动能定理得eE·Δx=ΔEp,则Ep-x图像的斜率,斜率k越大,电场强度E越大,因此x1处的电场强度比x3处的大,选项A 正确。Ep-x图像中x2处的斜率为零,则电场强度为零,最小;根据Ep=qφ可知,负电荷在电势低的地方电势能大,因此x2处的电势最小,选项B错误。当x＞x2时电子的电势能逐渐减小,说明静电力对电子做正功,则电场线方向沿x轴负方向,选项C错误。电子在电场中运动时只有静电力做功,则Ep+Ek=定值,因为电子在x=0处的电势能小于在x3处的电势能,所以电子在x=0处的动能大于在x3处的动能,在x=0处的速度大于在x3处的速度,选项D 正确。

8.BC 提示:当电路中的电流I=3 A时,该体重计测量的体重最大,根据欧姆定律得,变形得,即R=2 Ω,代入R=30-0.02F,解得F=1 400 N,选项A 错误,B 正确。踏板空载时F=0,代入R=30-0.02F,解得R=30 Ω,根据欧姆定律得,因此该体重计的零刻度线(踏板空载时的刻度线)应标在电流表G刻度盘的0.375 A 处,选项C正确,D错误。

9.BC 提示:磁场以速度v匀速向右移动,线框相对磁场向左运动,根据右手定则可知,图示时刻线框中的感应电流沿顺时针方向,选项A 错误。根据左手定则可知,列车所受的安培力方向向右,因此列车行驶的方向与磁场移动的方向相同,选项B 正确。当列车速度为v′时,列车相对磁场的速度大小为v-v′,则感应电动势E=2NBL(v-v′),感应电流,线框受到的安培力,选项C正确,D 错误。

10.BD 提示:当开关S闭合时,原线圈中的电流I1=2I+2I=4I,副线圈中的电流I2=I+I=2I,根据原、副线圈的匝数和电流成反比得,选项B正确。根据原、副线圈的匝数和电压成正比得,其中U2=U,则,a、b两端的电压,选项A 错误。当开关S断开时,副线圈中的电流减小,则原线圈中的电流也减小,灯泡L1和L2并联部分的电压减小,灯泡L1、L2都变暗,a、b两端的电压不变,则原线圈两端的电压增大,副线圈两端的电压也增大,电压表的示数增大,选项C 错误,D 正确。

11.(1)D (2)乙 (3)如图3所示(4)1.73 2.03

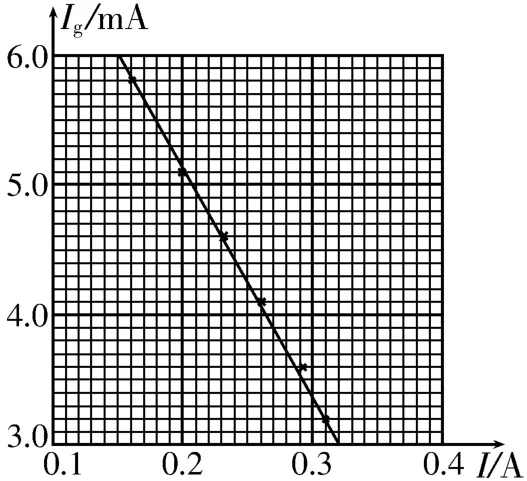
图3

提示:(1)根据欧姆定律得R0=,因为电阻箱R0的精确度为0.1 Ω,所以选项D正确。(4)根据闭合电路欧姆定律得E=Ig(Rg+R0)+I(r+RA),整理得Ig=,即Ig-I图像为斜率为负的倾斜直线,图像斜率大小,解得r=2.03 Ω。将Ig=3.0 mA,I=0.32 A 代入,解得E=1.73 V。

12.(1)在小球从A点运动到B点的过程中,根据动能定理得(mg+qE)L=,解得小球运动到B点时的速度大小。当小球运动到B点时,根据牛顿第二定律得F-(mg+qE)=,解得轻绳的拉力F=3(mg+qE),即轻绳的最大张力为3(mg+qE)。(2)小球离开B点后做类平抛运动,到达C点时小球垂直打在挡板上,则小球运动到C点时的速度大小。(3)在小球从A点运动到C点的过程中,根据动能定理得,又有UAC=EhAC,解得。

13.粒子带正电,根据左手定则可知,粒子在磁场中沿顺时针方向做匀速圆周运动,粒子受到的洛伦兹力提供向心力,则,解得r=0.1 m=10 cm。粒子的临界运动轨迹如图4所示,根据几何关系得解得xA=12 cm,xB=8 cm。因此x轴上有粒子穿过的坐标范围是-8 cm≤x≤12 cm。

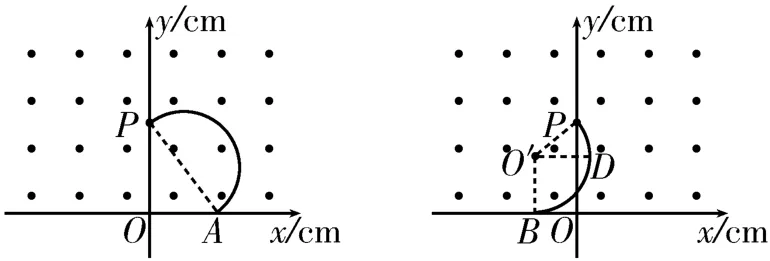
图4

14.(1)当金属杆ab做匀速运动时,根据平衡条件得F=μmgcosα+mgsinα+F安,其中,解得F=5.8 N。当金属杆ab的速度为0.4 m/s时,有0.8 N。根据牛顿第二定律得F-μmgcosα-mgsinα-F安1=ma,解得a=2.4 m/s2。(2)在0～1 s时间内,根据动量定理得mv2-0,其中,解得q=0.85 C。(3)从金属杆ab开始运动到它刚好达到稳定状态的过程中,根据动能定理得0,又有,解得Q杆=1.837 5 J。

15.(1)将速度v0沿x轴和y轴分解得,粒子在电场中做类平抛运动,即在水平方向上做匀速直线运动,在竖直方向上做匀加速直线运动,则,联立以上各式解得。(2)粒子从M点运动到N点的轨迹如图5甲所示,根据几何关系可得,每段轨迹圆弧所对圆心角均为,根据粒子受到的洛伦兹力提供向心力得qv0B=,解得。粒子从M点运动到N点所用的时间,解得t=。(3)此次粒子的运动轨迹与小圆相切,如图5 乙所示,根据几何关系得(r+R)2=r2+(3R)2,解得r=4R。根据粒子受到的洛伦兹力提供向心力得,解得v=2v0,根据动能定理得,解得。因此此次粒子释放时的位置坐标为。

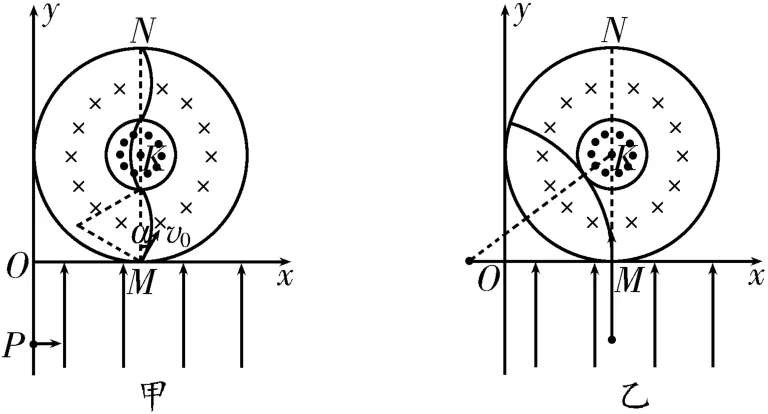
图5