轨迹圆法与动量定理法解决带电粒子在磁场中运动问题的对比

■河南省开封高级中学 毛炜翔

利用轨迹圆法分析带电粒子在磁场中运动问题的一般步骤为:画轨迹、定圆心、求半径、结合题意或临界条件列辅助方程求解相关问题。利用轨迹圆法分析求解时对几何关系和数学运算能力的要求较高,解题过程相对复杂。若借助动量定理分析带电粒子在磁场中的运动问题,则对粒子运动轨迹的描绘、圆心的确定和半径的求解等的要求都不高,常常可以获得事半功倍的效果,给人另辟蹊径的感觉。

一、借助动量定理处理带电粒子在磁场中运动问题的理论分析

如图1所示,带正电粒子在垂直于纸面向里的匀强磁场中运动,速度大小为v,所受洛伦兹力f=qvB。根据运动的分解可将速度v沿x轴、y轴分解为vx和vy,与两个分速度相对应的两个洛伦兹力分量分别为fx=qBvy(力的方向沿x轴,与vy垂直),fy=qBvx(力的方向沿y轴,与vx垂直),则沿x轴方向根据动量定理得-∑fx·Δt=mΔvx,即-∑qBvy·Δt=mΔvx,变形得-qBy=mΔvx,同理沿y轴方向有∑fy·Δt=mΔvy,即∑qBvx·Δt=mΔvy,变形得qBx=mΔvy。

图1

观察上述表达式可以发现,带电粒子在磁场中运动的过程中,借助运动的分解和动量定理计算时,粒子在x轴方向上的动量变化与在y轴方向上的运动距离有关联;粒子在y轴方向上的动量变化与在x轴方向上的运动距离有关联。

二、利用轨迹圆法和动量定理法处理带电粒子在磁场中运动问题的对比

例1如图2所示,质量为m,带电荷量为q的粒子从直线边界上的A点射入磁感应强度为B的匀强磁场区域,速度大小为v,方向与边界线间的夹角为θ,并从同一边界线上的B点飞出,求A、B两点之间的距离。

图2

解法一:轨迹圆法。

根据带电粒子在单直线边界匀强磁场中运动的对称性可知,粒子飞出磁场时的速度大小不变,速度方向与边界线间的夹角仍为θ,运动轨迹如图3所示。设带电粒子在磁场中运动的轨迹半径为r,根据洛伦兹力提供向心力得解得。 设A、B两点之间的距离为dAB,根据几何关系得dAB= 2rsinθ,解得dAB=。

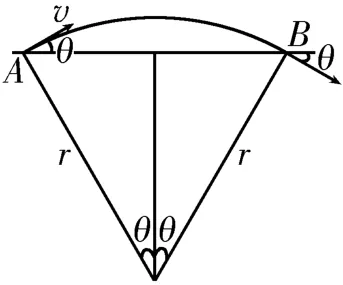
图3

解法二:动量定理法。

根据带电粒子在单直线边界匀强磁场中运动的对称性可知,粒子飞出磁场时的速度大小不变,速度方向与边界线间的夹角仍为θ,运动轨迹如图4所示。设带电粒子入射点A和出射点B之间的距离为dAB,则其大小与垂直于边界线方向的动量变化有关,根据动量定理得,解得。

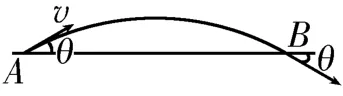
图4

点评:比较两种解法的解答过程可以发现,借助动量定理求解时,避开了复杂的作图和数学运算,但需要注意的是位移方向与动量变化方向两者之间的垂直关系。

例2如图5所示,真空中宽为d的区域内分布着匀强磁场,磁场方向垂直于纸面向里,质量为m,带电荷量为-q的粒子以与边界CD成θ角的速度v0垂直射入磁场中。要使粒子必能从边界EF上射出,则匀强磁场的磁感应强度应满足什么条件?

图5

解法一:轨迹圆法。

粒子从入射点A进入磁场后在洛伦兹力的作用下做匀速圆周运动,要使粒子必能从边界EF上射出,则相应的临界轨迹必为过点A并与边界EF相切的圆弧,如图6所示,作出粒子在A、P两点时的速度的垂线相交于O点,则O点即为该临界轨迹的圆心。设临界轨迹圆的半径为R0,根据几何关系得,解得。因此粒子必能从边界EF上射出的运动轨迹圆的半径R≥R0,即解得。

发电机振动评价不仅在电动机行业也在风力发电行业作为评价一个电动机能不能可靠运行的重要指标[4]，目前国内外对发电机振动问题也做了很多研究，而在弹性支撑选择对发电机振动影响方面研究的还是比较少的。本文以某款双馈风力发电机为原型，对其在两种刚度弹性支撑下进行模态仿真分析，对比弹性支撑刚度对发电机振动频率的影响，进而寻找更有效的减少发电机振动的措施。

图6

解法二:动量定理法。

粒子从入射点A进入磁场后在洛伦兹力的作用下做匀速圆周运动,要使粒子必能从边界EF上射出,则相应的临界轨迹必为过点A并与边界EF相切的圆弧,粒子射出磁场时的速度方向沿边界EF向下,设粒子在垂直边界EF方向上的位移为d,其数值大小与平行于边界EF的动量变化有关。以粒子的末速度方向为正方向,根据动量定理得,解得B0=。要使粒子必能从边界EF上射出,则匀强磁场的磁感应强度B≤。

点评:利用动量定理求解此题时用到了运动的分解和动量定理公式,不需要画轨迹、定圆心、求半径,求解过程更加简捷。

例3(2020年高考天津卷)如图7所示,在xOy平面的第一象限内存在方向垂直于纸面向里,磁感应强度为B的匀强磁场。一带电粒子从y轴上的M点射入磁场,速度方向与y轴正方向之间的夹角θ=45°。粒子经过磁场偏转后在N点(图中未画出)垂直穿过x轴。已知OM=a,粒子的电荷量为q,质量为m,重力不计。则( )。

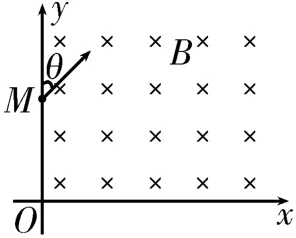
图7

A.粒子带负电荷

C.粒子在磁场中运动的轨迹半径为a

解法一:轨迹圆法。

粒子向下偏转,受到的洛伦兹力斜向下,根据左手定则可知,粒子带负电荷,选项A 正确。粒子的运动轨迹如图8所示,根据粒子的速度方向与y轴正方向之间的夹角θ=45°可知,∠OMO1=∠OO1M=45°,OM=OO1=a,则粒子在磁场中运动的轨迹半径,根据洛伦兹力提供向心力得,解得,选项B、C错误。根据几何关系得N点与O点之间的距离,选项D 正确。

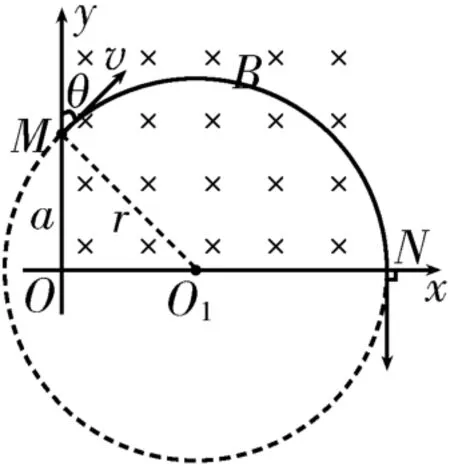
图8

解法二:动量定理法。

粒子向下偏转,受到的洛伦兹力斜向下,根据左手定则可知,粒子带负电荷,选项A 正确。根据题意可知,粒子运动的初、末状态如图9所示,粒子在磁场中运动的过程中,沿y轴方向的位移大小为a,其大小与粒子在x轴方向上的动量变化有关。因为粒子在N点垂直穿过x轴,所以粒子沿水平方向的分速度由减小为0,根据动量定理得-qBa=,解得,则粒子在磁场中运动的轨迹半径,选项B、C错误。同理,设N点与O点相距为Δx,其大小与粒子在y轴方向上的动量变化有关。设沿y轴向上为正方向,根据动量定理得-qBΔx=(-mv)-mvcosθ,解得,选项D 正确。

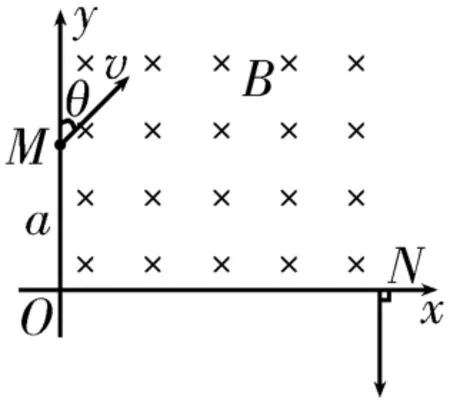
图9

答案:AD

点评:对比两种解法可以看出,巧妙运用动量定理求解带电粒子在磁场中运动相关问题时,更加关注的是粒子在初、末状态时的动量变化,以及相对应的距离。

例4如图10所示,真空中存在一宽度为d,磁感应强度为B的匀强磁场,磁场方向垂直于纸面向外,相互平行沿竖直方向的虚线M、N是磁场的左右边界线。O是边界线M上的一点,从O点平行于纸面向磁场区域发射速率为v的某种带正电的粒子,粒子射入磁场时的速度方向与边界线M成α=53°角,粒子从边界线N上某点飞出磁场,速度方向与边界线N成β=37°角(图中未画出),不计粒子自身重力,已知sin 37°=0.6,cos 37°=0.8。

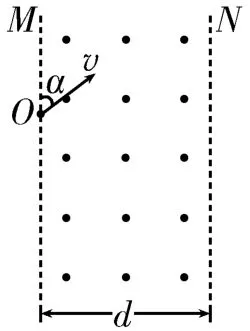
图10

(2)为了使得粒子不从边界线N上射出,沿平行于纸面,水平向左的方向加上匀强电场,则该电场的场强需要满足什么条件?

解析:(1)粒子穿越磁场的过程中,在水平方向上的位移为d,其大小与粒子在竖直方向上的动量变化有关。取竖直向下为正方向,根据动量定理得,解得。

(2)若粒子不能从边界线N上射出,则临界条件为粒子的运动轨迹与边界线N相切。设粒子运动到边界线N上时的速度大小变为v′,粒子在叠加场中运动时只有静电力做功,根据动能定理得。因为粒子受到的静电力方向水平向左,对沿竖直方向的动量变化无影响,而粒子在叠加场中运动的过程中,沿竖直方向的动量变化大小与其在水平方向上的位移d有关,所以可以在竖直方向上列动量定理方程,取竖直向下为正方向,则qBd=mv′-(-mvcosα),解得。

点评:施加电场以后,粒子的运动轨迹不再是圆周,无法使用画轨迹、定圆心、求半径的常规方法求解半径,无法进而求解粒子运动到边界线N上时的速度v′。借助动量定理,仅需考虑粒子沿竖直方向初、末状态的动量变化及沿水平方向的位移,便可轻松求得速度v′,使得题目的求解达到“柳暗花明又一村”的境界。

综上所述,借助动量定理解决带电粒子在磁场中的运动问题,避开了利用轨迹圆法处理相关问题时的“画轨迹、定圆心、求半径”等步骤,更加关注的是粒子在初、末状态时沿x轴和y轴的距离及与距离相对应的动量变化。当然,轨迹圆法是解决此类问题的常用方法,同学们应当牢牢掌握并能熟练运用。而利用动量定理处理带电粒子在磁场中的运动问题,给同学们提供了一种全新的解决问题的方法和技巧,可以开拓思维,提高解题能力,提升学科素养。