不确定条件下高超声速俯冲弹道鲁棒优化*
2022-03-20王培臣张睿轩闫循良
王培臣,张睿轩,闫循良
(1.西北工业大学 航天学院·西安·710072;2.中国航空工业空气动力研究院·沈阳·110034)
0 引 言
高超声速滑翔飞行器通常采用大升阻比气动外形,可进行长距离机动飞行,具有飞行速度快、机动灵活、突防效率高等特点,因此得到了各军事强国的广泛关注。弹道优化设计作为高超声速滑翔飞行器研究的难点与热点问题之一,吸引了大量国内外学者对此开展研究[1-5]。俯冲攻击段作为高超声速滑翔飞行器的最后飞行段[6],对于飞行器能否精确命中目标至关重要,因此也得到了相应的关注。徐明亮等[7]利用伪谱法对临近空间飞行器铰链力矩最小的俯冲弹道进行了优化设计,得到近似垂直的攻击弹道,但未考虑实际飞行过程中的随机干扰。乔浩等[8]利用高斯伪谱法对高超声速滑翔飞行器俯冲段翻身下压问题进行了优化,得到了高安全性的快速下压轨迹,但同样未考虑不确定因素影响,设计结果过于理想。
虽然针对俯冲段轨迹优化问题已有大量研究,但是传统的优化设计方法尚未考虑不确定性因素的影响[7-8]。然而,俯冲段飞行速度大,飞行状态及环境变化剧烈、复杂,所受气动力热环境恶劣,且高超声速滑翔飞行器的控制能力有限,因此,不能忽视不确定性因素对弹道的影响和制导控制系统的干扰。为保证俯冲攻击落点精度,提高弹道抗干扰能力,有必要对俯冲攻击段轨迹进行鲁棒优化。
目前,分析不确定性因素对轨迹影响的主要方法有:蒙特卡罗打靶分析法[9]、无迹变换法[10]、混沌多项式法[11-12]以及线性协方差分析法[13-15]等,而针对如何提高弹道抗干扰能力的相关研究较少。文献[14]将鲁棒性指标引入到滑翔炮弹轨迹优化中,得到的计算结果较为理想。因此,本文借鉴其思路,在传统高超声速滑翔飞行器弹道优化方法的基础上,引入鲁棒性设计指标,以降低不确定性因素干扰的影响,进而提升弹道抗干扰能力,同时降低制导控制系统负担。
1 俯冲运动数学模型
1.1 滑翔飞行器俯冲段动力学建模
由于目前高超声速滑翔飞行器普遍采用腹部防热设计,考虑到飞行器在俯冲段的热载荷较大,可在此过程中采用翻身下压策略[8]。即飞行器采用正攻角翻身飞行,利用有防热设计的腹部迎接来流,同时也可满足弹道快速下压需求。此外,考虑到俯冲段飞行时间较短,因此可忽略地球自转及扁率影响。因此,俯冲段三自由度质心运动模型可描述为
(1)
式中,h、λ、φ为飞行器位置参数,分别为飞行高度、地心经度、地心纬度;V、θ、σ为飞行器速度参数,分别为飞行速度、速度倾角、速度偏角;m为飞行器质量;α、υ为飞行器控制变量,分别为攻角和倾侧角;L、D为飞行器的升、阻力,计算公式如下
(2)
式中,ρ为大气密度;S为飞行器参考面积;CL、CD为飞行器气动升、阻力系数。
1.2 不确定性因素建模
在实际飞行过程中,高超声速滑翔飞行器会受到多种不确定性因素干扰,从而使得实际飞行弹道偏离理论轨迹。结合滑翔俯冲段飞行环境特点和飞行特性,本文考虑的不确定性因素主要有气动力模型偏差、大气模型偏差、阵风干扰偏差以及初始点状态偏差。
1.2.1 气动力模型偏差
由于地面实验无法准确模拟实际飞行环境,以及制造加工工艺和飞行加热烧蚀带来的误差,使得弹体气动力系数存在较大的偏差和不确定性,同时大气参数偏差也会导致飞行器实际气动力与理论设计值存在偏差,但气动力系数随马赫数与攻角的变化规律不变,所以实际气动力系数可表示为
(3)
式中,基准值CD0、CL0为计算或实验所得飞行器气动力系数;Ncd、Ncl为相互独立,且服从标准正态分布的随机变量;σcd、σcl代表实际气动力系数偏离基准值的程度,假设偏离值置信度(3σ)为基准值的15%,则有
σcd=σcl=15%/3
(4)
1.2.2 大气模型偏差
通常弹道仿真计算中应用标准大气模型,但实际大气参数与标准参数会存在一定偏差,主要为温度偏差和大气密度偏差。由于当地声速主要由温度决定,因此温度偏差会对声速的计算产生影响,进而影响马赫数的计算。而气动力系数通过马赫数与攻角插值得到,所以温度偏差带来的干扰可在气动力偏差中加以考虑计算,故此处只考虑大气密度偏差。参考文献[14]给出了不同海拔下实际大气密度的标准差与标准大气密度的比值关系,基于此关系,实际大气密度可计算如下
(5)
式中,ρ0为标准大气密度;Nρ为服从标准正态分布的随机变量。
1.2.3 阵风干扰偏差
在飞行器翻身下压飞行过程中,阵风干扰会使得质心运动产生随机扰动,主要体现在对速度大小和方向的影响,因此要考虑阵风对速度参数产生的影响,即有以下关系
(6)

1.2.4 初始点状态偏差
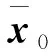
(7)
2 基于线性协方差分析的误差传播建模
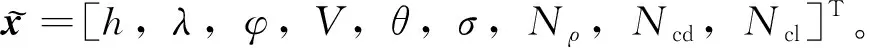
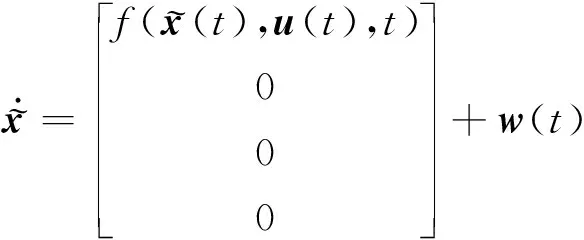
(8)
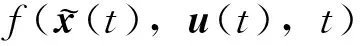
E(w(t)w(t)T)=R(w)
(9)
式中,R(w)为谱密度矩阵,为
(10)
故根据不确定环境下的系统模型,可得状态量的协方差矩阵为
(11)

(12)
式中,对角线各项为实际状态偏离基准值的方差。当参考轨迹给定后,协方差矩阵P可通过如下李雅普诺夫方程求解
(13)
式中,A为雅可比矩阵,由于数值求解雅可比矩阵计算量大,为提高计算速度,推导如下解析表达式进行计算

(14)

(15)
3 弹道优化模型
落点散布大小是衡量弹道抗干扰能力的重要指标之一。为增强俯冲弹道对不确定性因素的抗干扰能力,可以将落点散布大小作为代价函数。在满足过程约束的前提下,当优化得到代价函数的值最小时,即可认为得到的优化弹道抗干扰能力最强,因此构建如下代价函数
(16)
式中,右端第一项代表落点散布,ω为权重系数,其取值可表征轨迹抗干扰能力的大小;第二项保证飞行器实际工作中,控制量相对光滑且不会发生突变。
分析代价函数式可知,ω=0时,即代价函数中不考虑轨迹抗干扰能力,问题将退化为传统的俯冲攻击段最优弹道求解问题;ω>0时,则该问题为考虑轨迹抗干扰能力的鲁棒轨迹优化问题。
同时,优化过程中应满足下列约束条件:
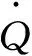
(17)
式中,K为常值,其取值与飞行器结构相关。
2)控制约束
(18)
(19)
3)终端约束
(20)
通过以上建模过程,即可将提高弹道抗干扰能力问题转化为多约束条件下的最优控制问题。目前求解最优控制问题主要有间接法与直接法两种。前者很难处理复杂约束条件下的最优控制问题,相反地,直接法更适合求解这类问题。在众多直接法中,高斯伪谱法以较少的参数和较高的精度优势,已广泛应用于复杂约束条件下的轨迹优化问题[5,16]。因此,本文选用高斯伪谱法作为求解最优控制问题的方法。
4 算例仿真与分析
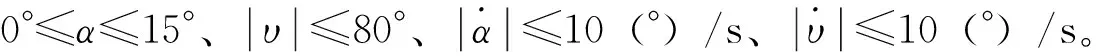
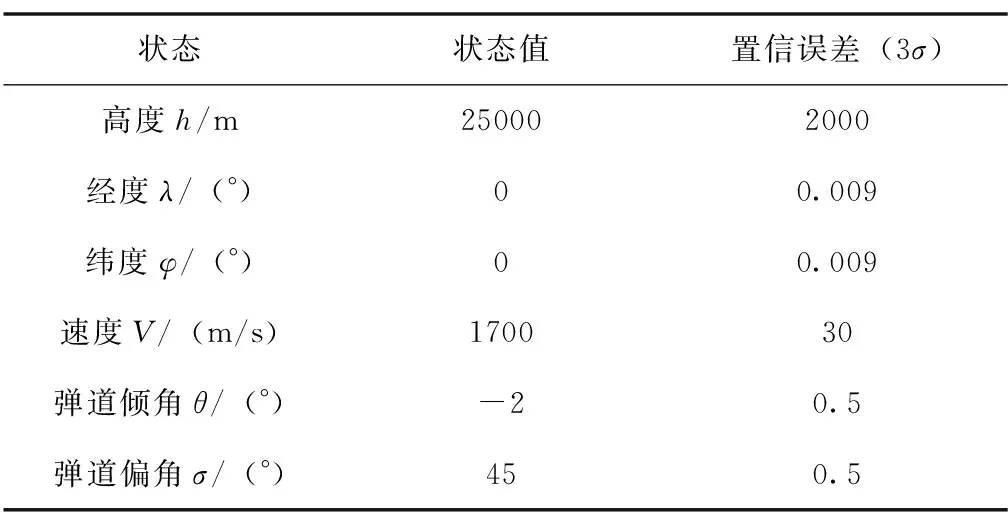
表1 初始状态

表2 阵风干扰高斯白噪声功率谱密度
为验证LinCov方法的可行性,取ω=0进行弹道优化仿真,并基于优化结果利用LinCov方法和蒙特卡罗打靶法(Monte Carlo,MC)计算得到终端误差,如表3所示。可以发现,由LinCov方法得到的落点经度方差与蒙特卡罗打靶法得到的结果相对误差为1.77%,得到的纬度方差相对误差为6.99%。图1分别给出了两种方法得到的落点分布3σ误差椭圆,也可以看出两种方法的落点分布范围相差不大,验证了线性协方差分析法估计终端经纬度散布的可行性。

表3 线性协方差分析法与蒙特卡罗打靶法结果对比
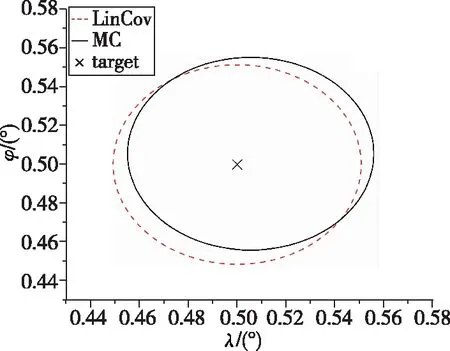
图1 线性协方差方法和蒙特卡罗打靶法落点3σ误差圆对比Fig.1 Comparison of 3σ position error ellipses between linear covariance analysis and Monte Carlo shooting methods at target without considering the influence of uncertain factor
为验证鲁棒轨迹优化算法的可行性,取ω=0.1和1,结合线性协方差分析法和高斯伪谱法进行弹道优化,所得最优弹道对应的攻角、倾侧角控制量曲线分别如图2、图3所示。对比控制量曲线可以发现,随着权重系数的增大,控制量的变化更剧烈,说明为了提高轨迹对不确定性因素的抗干扰能力,需要消耗一定的控制量裕度,且随着权重系数ω的增大,控制裕度消耗的程度增加。
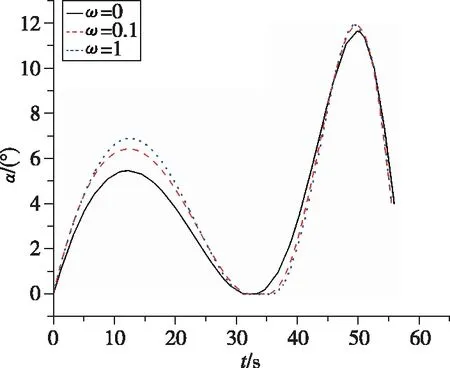
图2 攻角随时间变化曲线Fig.2 Time histories of the attack angle variables
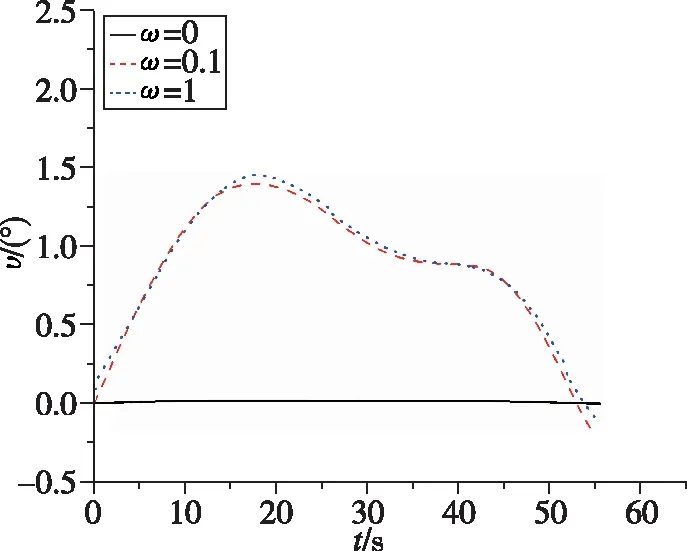
图3 倾侧角随时间变化曲线Fig.3 Time histories of the tilt angle variables
下面对不同权重下的弹道优化结果进行蒙特卡罗打靶仿真,并统计落点分布情况。表4、表5分别给出了落点分布的均值和方差。当ω=0.1时,落点分布均值与目标值在经度方向偏差为0.009°,纬度方向偏差为0.008°;其落点分布方差与ω=0的结果相比,经度分布方差减小55.12%,纬度分布方差减小52.57%,落点分布范围明显减小,表明本文方法可有效地提高弹道抗干扰能力,降低弹道对不确定性因素的敏感度。而对比ω=0.1和ω=1时的落点分布均值和方差可知,后者的数据较前者都有所提升,但差异并不大,说明随着权重系数ω的进一步增加,落点散布减小但效果有限。因此,在实际应用时,需要设置权重系数ω以权衡控制量裕度与落点密集度之间的关系,在控制允许范围内可适当增大权重系数ω以尽可能降低落点散布。

表4 不同权重情况下优化结果的蒙特卡罗打靶落点均值对比
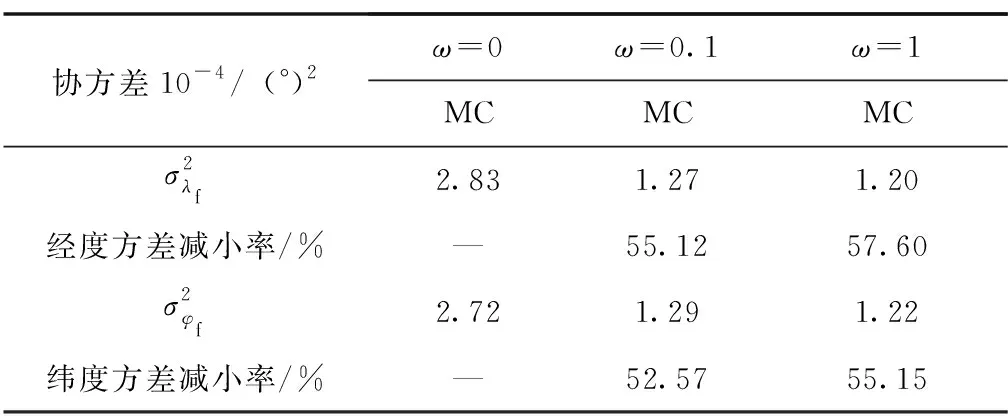
表5 不同权重情况下优化结果的蒙特卡罗打靶落点方差对比
为更直观地表示上述蒙特卡罗打靶落点分布情况,图4与图5分别给出了ω=0和ω≠0时的落点分布3σ误差椭圆及落点散布,与表4、表5中的结果相对应。由图4、图5可知,ω≠0时落点分布范围明显减小,说明弹道抗干扰能力明显增加。但随着权重系数的进一步增加,落点散布椭圆几乎不变。这是由于打靶过程使用开环控制,没有加入反馈信号,不确定因素的存在使得落点散布的减小有一个极限。
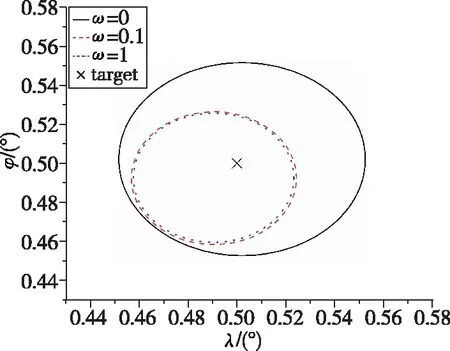
图4 不同权重情况下优化结果蒙特卡罗打靶落点3σ误差圆对比Fig.4 Comparison of 3σ position error ellipses based on optimization results under different weights

(a) ω=0
5 结 论
本文将线性协方差分析方法和高斯伪谱法相结合,建立了一种考虑不确定性因素的弹道鲁棒优化模型及算法。对鲁棒优化弹道结果进行蒙特卡罗打靶验证,得到了以下结论:
1)当优化目标中考虑落点精度时,蒙特卡罗打靶的落点分布范围明显减小,说明本文优化方法能明显提高弹道的抗干扰能力;
2)由于打靶过程使用开环控制,没有加入反馈信号,不确定因素的存在使得误差减小有一个极限。因此,进一步增加目标函数中的权重系数对于打靶结果改善有限。
