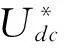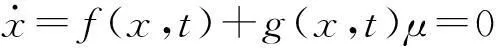基于反馈线性化的静止同步串联补偿器变结构潮流控制研究
2015-12-30贺双双曹建军陈智迪
贺双双,曹建军,陈智迪
(1.武汉金中石化工程有限公司,湖北 武汉 430000;2.湖北能源集团,湖北 武汉 430000)
基于反馈线性化的静止同步串联补偿器变结构潮流控制研究
贺双双1,曹建军1,陈智迪2
(1.武汉金中石化工程有限公司,湖北 武汉430000;2.湖北能源集团,湖北 武汉430000)
摘要:静止同步串联补偿器(static synchonous series compensator,SSSC)是一种调节线路潮流和接入点电压的FACTS装置,采用输入-输出反馈线性化处理SSSC含滤波电容方程的5阶非线性等效数学模型,得到一个带约束条件的线性方程,运用变结构控制理论设计了SSSC的变结构控制器。最后利用Matlab/Simulink仿真验证了所设计的控制器达到了SSSC的控制潮流的效果,与PI控制相比,其性能有一定的优越性。
关键词:静止同步串联补偿器;输入-输出线性化;变结构控制;抗干扰能力
0引言
静止同步串联补偿器(static synchonous series compensator,SSSC)是常见的第二代柔性交流输电装置,它是通过串入一个可变电压来调节线路潮流和接入点电压[1-3]。SSSC常见的控制方式主要包括PI(proportiona integral)控制、智能控制和非线性控制,非线性控制方法是近年应用在SSSC中比较普遍的一种方法[4-5]。文献[6]分别从定阻抗和定电压两种控制角度,运用逆系统滑模控制分别对SSSC进行了控制设计,这种设计方法本质上是PI和滑模混合控制,增加了协调控制的难度。文献[7]利用直接反馈线性化方法处理SSSC的3阶动态模型,未考虑SSSC中滤波电容的动态变化过程。文献[8]运用微分几何方法处理含SSSC的单机无穷大系统,结合线性最优控制理论,得到了SSSC的非线性最优控制策略。文献[9]建立了SSSC的多变量仿射非线性模型,用精确反馈线性化方法设计了SSSC的非线性多输入多输出控制器。考虑了SSSC中的滤波电容影响和常规d-q轴分解的耦合问题,给出了SSSC在αβ坐标系下的5阶非线性等效数学模型,该数学模型更加贴近SSSC运行特点,采用输入-输出反馈线性化处理得到1个含2个约束条件的线性方程,运用变结构控制(也称为滑模控制)理论设计了SSSC的变结构控制器,并分析了所设计的控制器抗干扰性能。最后利用Matlab/Simulink仿真验证了所设计的控制器与PI控制相比响应更快,具有较好的鲁棒性。
1SSSC控制系统的反馈线性化
1.1 SSSC反馈线性化判别
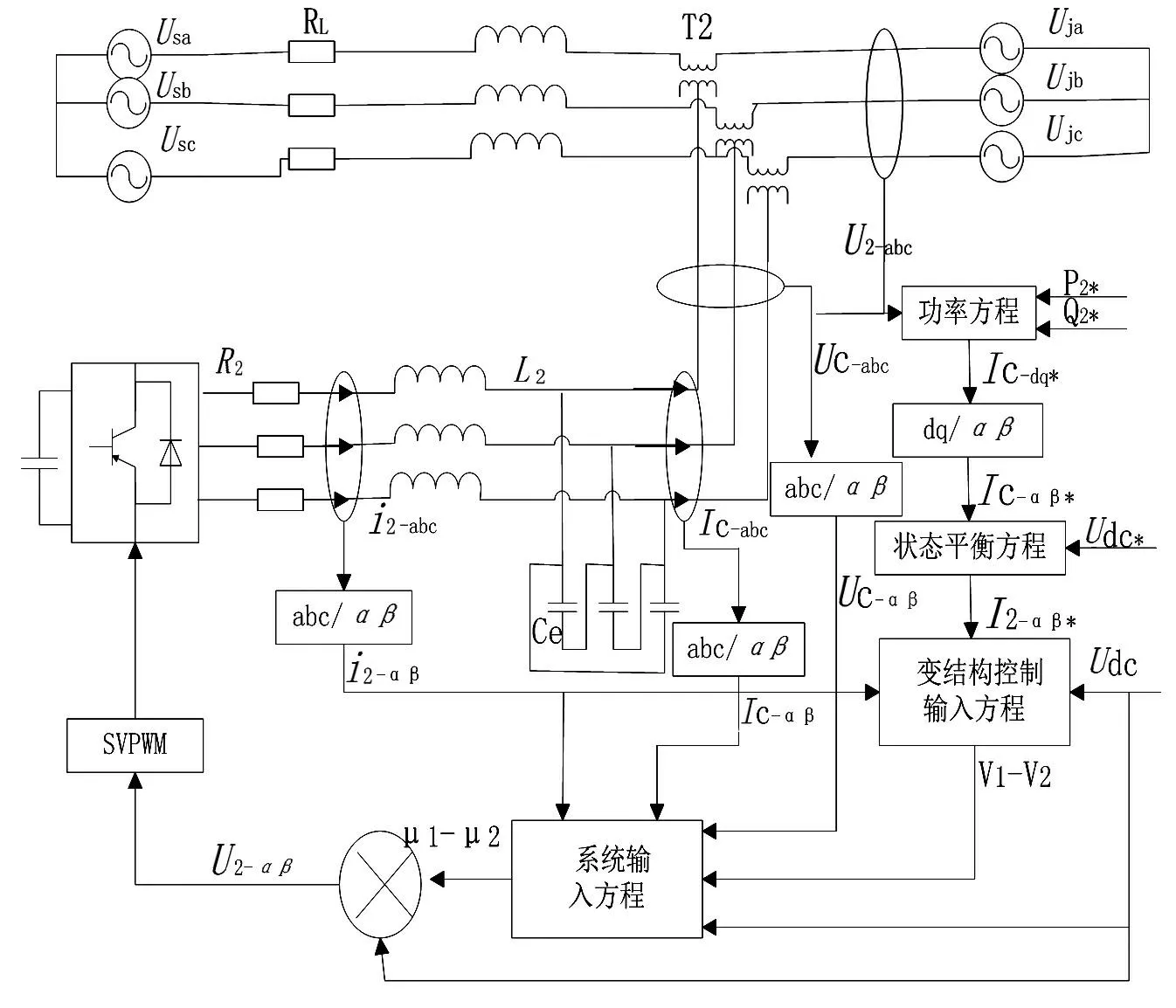
SSSC的等效电路图如图1所示,图中R2、L2、Ce分别为串联侧的滤波电感、等值电阻和滤波电容;C为直流侧电容;Udc为电容电压;P、Q分别是串联侧注入系统的有功功率和无功功率;u2a、u2b、u2c、i2-abc为逆变器的输出三相电压和输出三相电流;uac、ucb、ucc、ica、icb、icc为滤波电容侧的输出三相电压和输出三相电流;us为始端电压;uj为末端电压[10]。
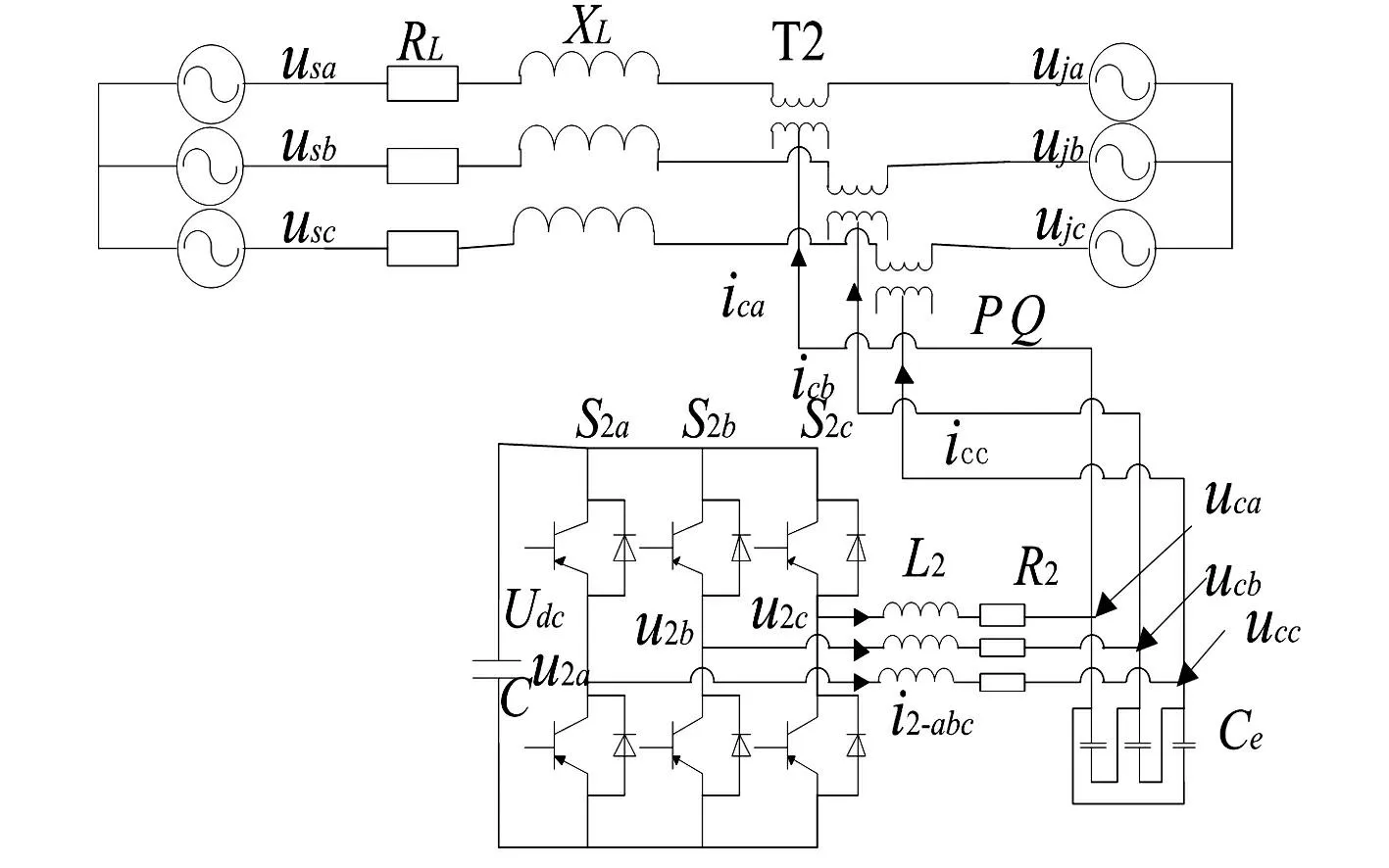
图1 SSSC的等效电路图
则SSSC在坐标系下的数学模型为
(1)
式中:u2j=s2jUdc;j=α,β;s2j为对应线路的开关信号函数。
将式(1)整理为式(2)所示的非线性系统标准形式[11-12],则有
(2)
式中:
x=[x1x2x3x4x5]
=[i2αi2βucαucβUdc]T
μ=[s2αs2β]T
y=[y1y2]T
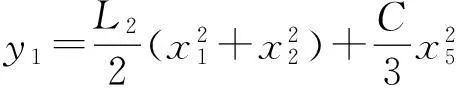
y=[y1y2]T=[h1(x)h2(x)]
(3)
根据文献[12]系统关系度的定义,先求得:
(4)
(5)
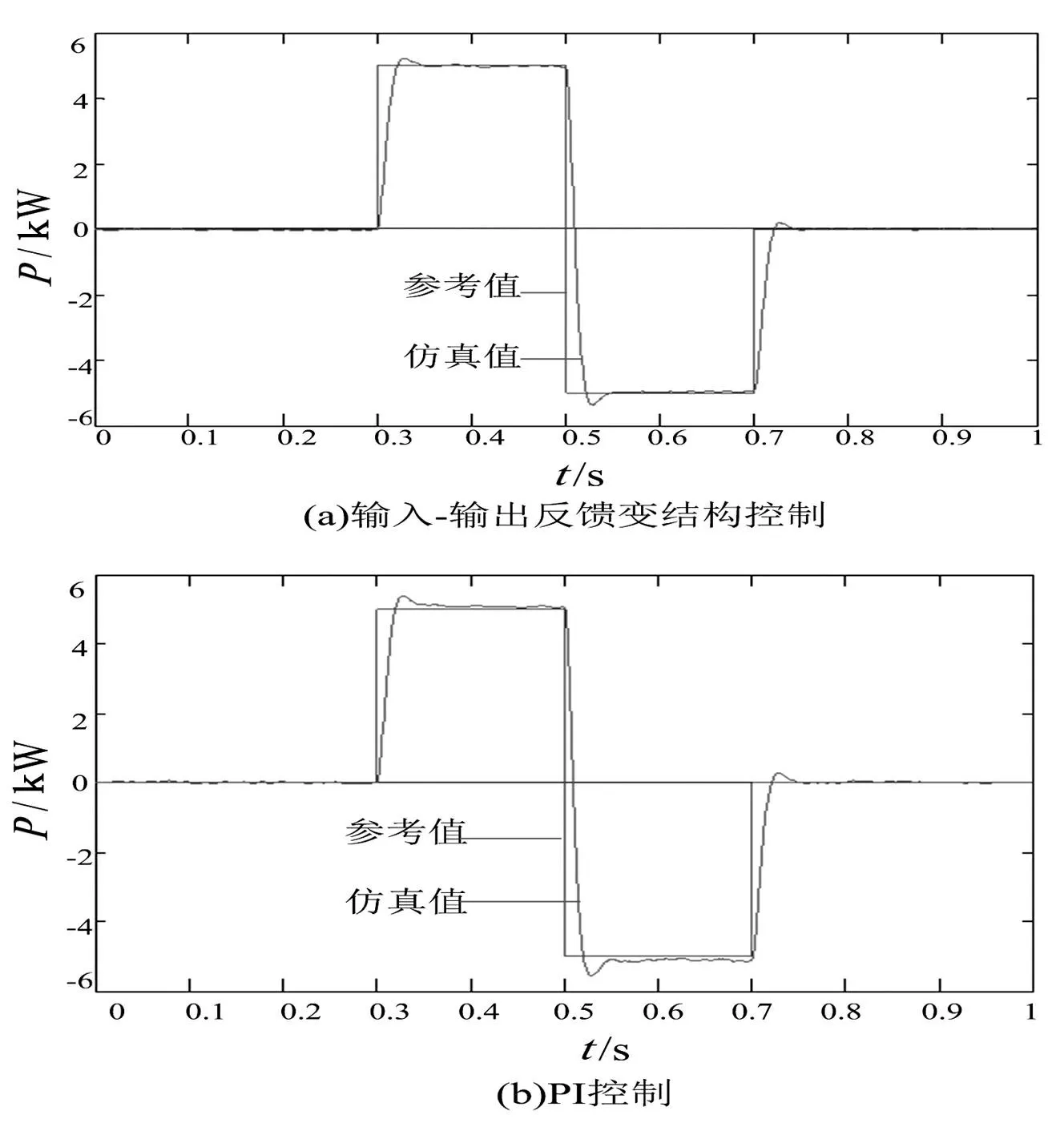
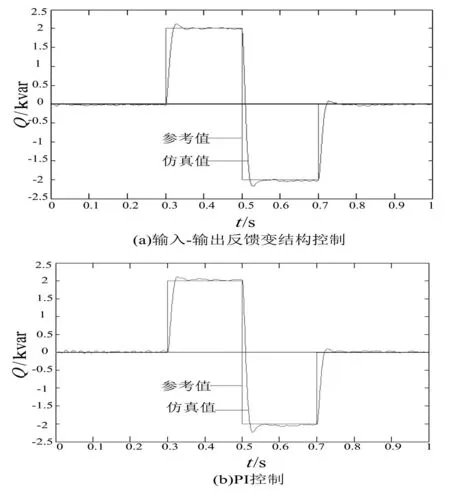
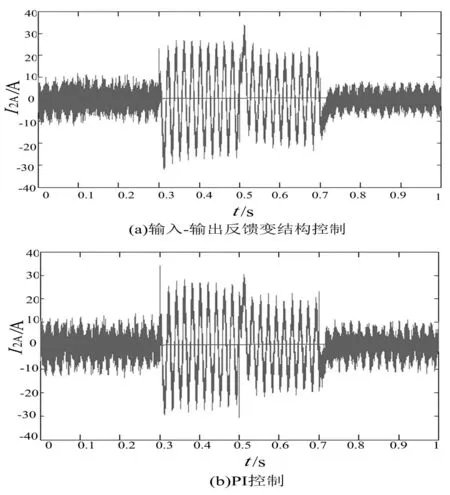
得到系统2个输出函数对应的关系度分别为r=[r1r2]=[21] SSSC是一个5输入-2输出系统,前面已经判断出系统只能进行输入-输出线性化处理,因此选择坐标变换: (6) 式中,φ1(x)、φ2(x)满足: 1) 2) 是满秩的,即z微分同胚。 系统的约束条件为 (7) 原非线性系统可以转化为含式(8)所示约束条件的Brunovsky标准型。 (8) 式中: 矩阵[BAB]的秩为3,所以该线性系统可控。 新的控制变量为 (9) 对于SSSC的系统的变结构控制策略,在满足式(7)所示的约束条件下,对于式(8)所示的线性系统,设y的期望输出信号为y*(下面带*的变量表示为其输出指令值),跟踪误差为 (10) 选取滑模面方程为 (11) 选取指数趋近律 (12) 结合式(8)和式(12)式可得滑模控制律为 (13) 代入式(9)中得到原非线性系统的控制律为 (14) 式中,c、ki、εi(i=1,2)为控制器设计参数,它们决定了控制系统的稳态和动态性能。 上节设计了SSSC的变结构控制器,下面对所设计的控制器抗干扰性能进行分析,当系统存在扰动时,系统线性化处理后的Brunovsky标准型可以表示为式(15)所示。 (15) 式中,α(z)、β(v)、γ(z)为原来非线性系统Δf(x,t)、Δg(x,t)的相对应不确定项,α(z)、β(v)、γ(z)有界,均小于某一常数。 将式(11)、式(13)代入式(15)得 (16) 式中,δi的取值为 (17) (18) 选取控制器参数 (19) (20) (21) 2仿真分析 所提出的SSSC输入-输出反馈线性化变结构控制框图表示如图2所示。为了验证该控制策略在电力系统中的有效性,在Matlanb/Simulink仿真平台上对其进行了仿真验证,并和PI控制(控制策略见参考文献[13])进行了对比,系统采用空间矢量脉宽调制(SVPWM),开关频率为5 kHz,潮流控制,仿真参数为:电网频率f=50 Hz;电源电压有效值Us=220 V,初相角为105°;输电线路等效电阻RL=2 Ω,LL=25 mH;串联变压器变比2∶1;串联侧滤波电感L2=2 mH;串联变流器等效电阻R2=0.01 Ω;滤波电容Cs=66 μF;直流电容C=4 700 μF;直流电压初始值Udc0=600 V。 系统控制参数:c=1 750,k1=k2=3 000;ε1=ε2=15;PI控制参数:电流环kp=16.5,ki=825;电压环kp=3,ki=4.5;功率环kp=0.001 3,k3=10;直流电容控制器kp=1.5,ki=0.5;仿真结果如图3~图7所示。 图2 SSSC控制框图 图3 SSSC注入系统有功功率 图3和图4为SSSC仿真模型中注入输电线路有功功率和无功功率,初始值都为0,在0.3 s时有功功率阶跃到5 kW,无功功率阶跃至2 kvar,在0.5 s时有功功率阶跃至-5 kW,无功功率阶跃至-2 kvar,在0.7 s时有功功率和无功功率恢复至0。由图中(a)、(b)对比可知,输入-输出反馈线性化变结构控制和PI控制都能较好地跟踪输电线路的有功和无功,但输入-输出反馈线性化变结构控制能在更小的超调量下进行跟踪。图5为输出电压响应曲线,当注入的有功功率为正值时,电容释放能量,直流电容电压略微下降,输出电压减小,当注入有功功率为负值时,电容充电,输出电压升高。图6为输出电流响应曲线,输出电流快速地跟踪潮流发生变化。图7为直流电容电压的仿真图,从图中可以看出尽管两种控制方式都能很好地跟踪潮流,但输入-输出线性化变结构控制明显能够更好地维持直流电容电压保持在600 V。 图4 SSSC注入系统无功功率 图5 SSSC输出交流电压 3结论 提出了一种新的SSSC变结构控制策略。基于输入-输出反馈线性化理论,通过选择合适的输出函数、坐标变换将SSSC的非线性模型转化为1个含约束方程的Brunovsky标准型,再通过变结构控制完成控制器的设计。仿真结果表明,与PI控制相比,该控制策略可以使系统获得更好的补偿效果,而且该方法响应快,对参数及扰动变化不敏感,具有一定的实际价值。 图6 SSSC直流电容电流 图7 SSSC直流电容电压 参考文献 [1]Hingorani N G,Laszion Gyugyi.Understanding FACTS Concepts and Technology of Flexible AC Transmission Systems in New York[J].The Institute of Electrical and Electronics Engineers,1999,22(3):104-106. [2]Philip M,Ashmole P.Flexible AC Transmission Systems Ⅱ Methods of Transmission Line Compensation[J].Power Engineering Journal,1996,10(6):273-278. [3]王仲鸿,沈斐,吴铁铮.FACTS技术研究现状及其在中国的应用与发展[J].电力系统自动化,2000,24(23):1-5. [4]张爱国,韩军锋,蒋程.基于神经网络自适应PI控制的SSSC潮流控制器[J].电力系统保护与控制,2010,38(22):15-19,24. [5]张爱国,张建华,蒋程.静止同步串联补偿器的恒阻抗模型及其双闭环控制策略[J].电网技术,2010,34(3):106-111. [6]钱碧甫,王奔,徐万良.SSSC滑模控制策略研究[J].电网与清洁能源,2011,27(7):39-42,46. [7]颜伟,吴文胜,华智明,等.SSSC非线性控制的直接反馈线性化方法[J].中国电机工程学报,2003,23(3):65-68. [8]李娟,周兴福,李淑琴.基于精确反馈线性化方法的SSSC非线性控制器[J].电网技术,2008,32(Z2):12-15. [9]赵洋,肖湘宁.基于微分几何方法的静止同步串联补偿器非线性控制[J].电工技术学报,2008,23(4):132-136. [10]刘永江.UPFC控制策略研究及其对电力系统的影响[D].成都:西南交通大学,2011:1-24. [11]焦晓红,关新平.非线性控制系统分析与设计[M].北京:电子工业出版社,2008:18-43,94-120. [12]高为炳.变结构控制的理论及设计方法[M].北京:科学出版社,1996:143-183. [13]黄崇鑫.统一潮流控制器控制策略的研究[D].成都:西南交通大学,2009:1-78. [14]Jiang X,Xiao X N,Zhao Y.Study on Main Circuit Selection and Single Phase SVPWM Algorithm of SSSC[C].2006 International Conference on Power System Technology,2006:1-6. 中图分类号:TM74 文献标志码:A 文章编号:1003-6954(2015)04-0056-06 作者简介: 贺双双(1989),助理工程师,硕士研究生,毕业于西南交通大学电气工程学院; 曹建军(1968),高级工程师,本科,毕业于新疆工学院; 陈智迪(1988),助理工程师,硕士研究生,毕业于西南石油大学电子信息学院。 (收稿日期:2015-05-04) Abstract:Static synchronous series compensator (SSSC) is a kind of FACTS devices to regulate line power flow and the voltage at access point. The fifth-order nonlinear mathematical model of SSSC containing filter capacitor equation is processed by input/output feedback linearization to acquire linear equations with the constraints, and then the variable structure controller of SSSC is designed using variable structure control theory. Finally, the simulation in Matlab/Simulink dynamic simulation platform verifies the designed controller can achieve the control effect for SSSC and has some advantages compared with PI control. Key words:static synchronous series compensator (SSSC); input/output linearization; variable structure control; anti-jamming capability1.2 SSSC输入-输出线性化
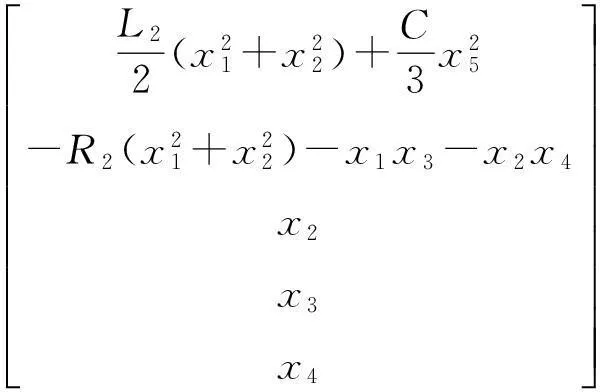
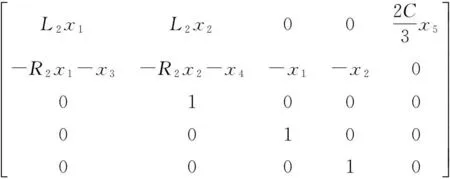


1.3 SSSC控制器设计
1.4 SSSC抗干扰性能分析


1.5 SSSC控制系统平衡点分析