高超声速飞行器的天基多尺度异步平台协同探测方法*

李洪昌，卢晓东，姚雨晗，霍俊鑫，柴锐波

(1.西北工业大学 航天学院·西安·710000；2.北京电子工程总体研究所·北京·100854)

0 引 言

随着科技的发展和进步，现代战场环境变得日益复杂，对于无人机等空中目标，使用单个传感器难以对目标进行持续有效的探测，易被干扰。而多个传感器可以在空间和时间上相互协调对目标进行探测，在提高精度的同时降低单个传感器因干扰造成对目标探测的影响，因此发展多传感器协同探测技术对提高目标探测精度具有重要意义[1]。目前在多传感器协同探测中，存在不同种类的传感器之间的采样率不同、数据质量不一致等问题[2]，此外，多传感器信息在通信过程中存在延迟丢包等问题[3]。因此，研究如何解决多传感器的异步融合和时间延迟问题是多传感器协同探测的关键技术。

传统的异步融合问题的解决方法主要有内插外推法、曲线拟合法、最小二乘法和序贯式处理方法[4]等，其中内推外插法和最小二乘法是目前应用较多的方法，但是这些算法实时性差，操作不够简便，并且很难获得最优解。文献[5]为解决空间目标分布式跟踪过程中的异步采样和时间延迟问题，提出了异步分布式信息滤波算法，其局部传感器的信息通过一定的网络拓扑结构进行传递，然后将采样信息按时间排序，使用了分布式框架对信息进行融合。文献[6]针对多传感器采样率不同且量测滞后的问题，提出了基于多尺度数据分块的信息融合算法，通过数据分块得到多尺度系统模型，将不同尺度上的观测信息滤波后,用简单凸组合法融合获得基于全局的状态估计值。文献[7]基于多尺度系统理论,研究了不同采样率下红外和激光传感器的数据融合方法，大大降低了滤波过程的复杂度，得到了最优的融合估计。但是这些研究主要侧重于解决异步融合问题，对于传感器延迟问题研究较少。

对于多传感器通信网络中的延迟问题，传统的内推外插法、最小二乘法等也可以解决。但这些算法用于事后处理效果较好，无法满足机动目标配准的实时性要求。文献[8]使用一组伯努利分布的随机变量描述传感器随机延迟情况，重新构建了系统模型，并设计了有/无时间戳情况下的最优线性滤波器。文献[9]也采用这种方法建立了系统模型，并设计了鲁棒估计器对系统状态进行估计，该方法可以降低传感器时间延迟对系统的影响，但是精度较差。文献[10]在当前测量未到达估计器时，将当前瞬间的传感器测量的预测器用作补偿器，与使用先前接收的最新测量的补偿估计量相比，所提出的估计量具有更高的估计精度和更小的计算负担，但是使用平滑方法处理延迟到达数据增加了计算和滤波器结构的复杂性。文献[11]通过使用测量重组技术，将随机延迟系统重构为等效无延迟系统，然后基于卡尔曼滤波技术设计最优线性滤波器，但是这种处理方法实时性较差。

本文针对多传感器协同探测中的时间配准即异步融合和时间延迟问题进行研究。首先，建立多尺度系统模型。其次，根据多尺度系统理论，对尺度递归融合算法进行改进，设计不同尺度间异步融合方法。然后，对融合中心的信息到达情况进行分析，利用有序加权平均策略算法解决通信网络中的时间延迟问题。最后，利用所研究算法进行多传感器协同探测数字仿真校验。

1 多尺度系统模型

x(k+1)=Φ(k+1,k)x(k)+w(k)

(1)

式中，x(k)为k时刻目标的状态向量；Φ(k+1,k)为离散化的系统状态转移矩阵；w(k)为零均值高斯白噪声，其方差为Q(k)。

传感器的量测模型通常为非线性的，离散化的传感器量测方程可以表示为

z(k)=h(x(k),k)+v(k)

(2)

式中，z(k)为传感器k时刻的量测值；h(x(k),k)为传感器非线性量测函数；v(k)为传感器的量测噪声，是均值为零的高斯白噪声，其方差为R(k)。

考虑到不同传感器之间的采样速率不同，根据多尺度系统理论，将不同传感器的采样率按照从高到低排列用i表示，同时不同的采样率也表示不同的尺度。具有最高采样率的传感器1对应于最细尺度，最粗尺度的传感器N具有最低的采样率。则有N个传感器进行观测的多传感器单模型线性系统描述为

(3)

式中，x(k)为最细尺度上k时刻的状态变量，且k1=k,x1(k1)=x(k)；Hi(ki)为不同速率传感器下量测函数对状态变量的雅可比矩阵，下标i为传感器尺度。

2 多速率传感器异步融合

2.1 多速率传感器间的异步处理

根据多尺度系统理论[12]，粗尺度i上的状态可以用较细尺度i-1上状态的低通滤波或滑动平均近似，从而可以将粗尺度上的信息转换到细尺度上。对各个尺度上的传感器信息进行独立滤波处理。然后从最粗的尺度开始，相邻两个尺度上的信息进行融合，逐步递归融合进而得到最细尺度上的多速率多传感器信息融合结果。

图1所示即为基于多尺度系统理论的尺度递归融合估计算法。但是从实际情况来看，不同的传感器位于不同的平台上，且各个平台之间的距离较远，通信时间长，该方法在应用过程中存在信息重复使用、计算复杂和滞后性等问题。另外，考虑到避免部分传感器受到干扰等因素影响协同探测系统整体的性能，宜采用抗干扰能力较强的分布式信息融合结构。于是结合融合算法和信息融合结构来考虑，以采样速率最高的传感器作为融合中心，将不同尺度上的信息直接与最细尺度上的信息进行融合，这样可以减少系统内各节点之间的通信需求，同时降低计算复杂度，图2即为改进的尺度融合估计算法流程。另外，由于各尺度上的信息经过滤波之后可以直接得到目标的相关状态，融合中心可以直接使用各节点的信息进行融合。

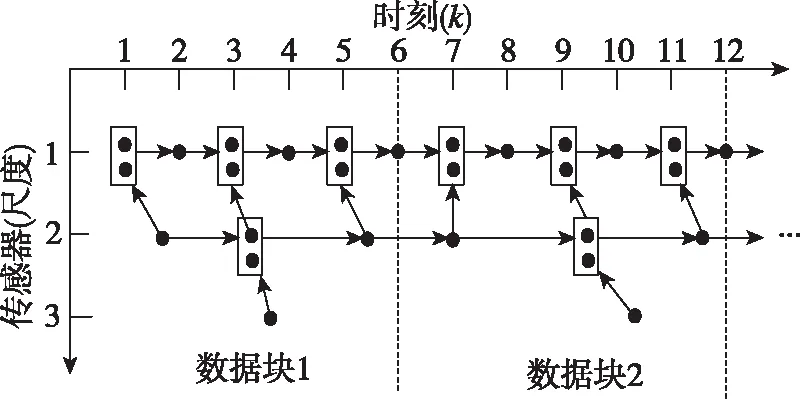
图1 尺度递归融合估计算法流程Fig.1 Scale recursive fusion estimation algorithm flow

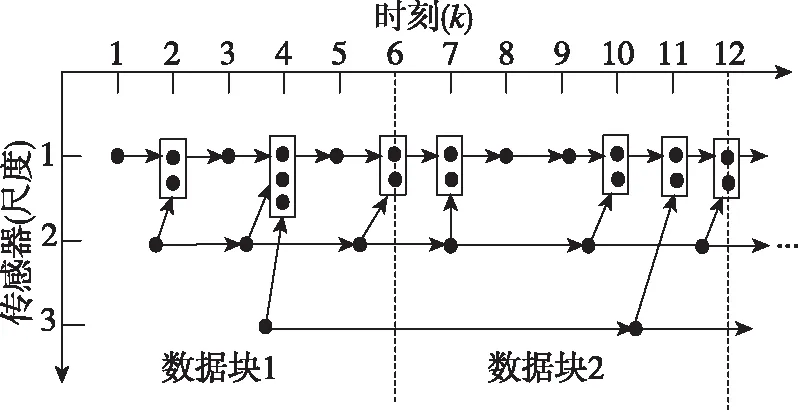
图2 改进的尺度融合估计算法流程Fig.2 Improved scale fusion estimation algorithm flow

2.2 尺度间传感器信息融合方法

有序加权平均策略(Ordered Weighted Averaging，OWA)信息融合算法，通过引入冗余向量作为预测系统中非线性和不确定性的标准，并使用过去一段时间内的传感器冗余向量来构造各尺度传感器信息在融合过程中的权重矩阵。然后，通过权重矩阵将各尺度传感器的信息进行加权计算，从而融合各尺度传感器的信息，最终得到目标状态信息。其中冗余向量定义如下

(4)

式中，yi(k)为k时刻传感器量测值。

但由于传感器量测方程为非线性方程，且量测矩阵不满秩，而仅有传感器信息的情况下，可以求解出目标的位置状态信息。故基于此重新构造冗余向量

(5)

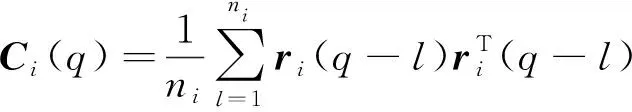
(6)

式中，Ci(q)为尺度i上第q个信息的权重矩阵；ni为尺度i上的采样率与尺度1的采样率之比；l为滑窗长度，一般可取为所有传感器采样率的公倍数。

假设融合中心每一个时刻参与融合的信息量为m(1≤m≤N)，对于式(3)所示的多传感器单模型系统，融合中心目标状态的计算方式为

(7)

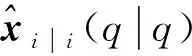
3 传感器网络中时间延迟情况处理

在传感器协同探测网络中，各节点间通信过程会不可避免地因为各种因素或干扰受到影响，导致传感器节点的信息出现时间延迟等问题，从而影响协同探测系统的信息融合工作。

如图3所示，融合中心的时间基准用圆点表示，即在这一时刻融合中心将各传感器节点的信息融合。传感器A的信息用矩形表示，传感器B的信息用三角形表示，信息指向融合中心的圆点表示传感器信息在融合中心进行处理之前已及时到达，在圆点之后表示因为某些原因传感器的信息未能及时到达。排除通信网络瘫痪的情况，融合中心在每一时刻都应该至少接收到一个传感器节点的信息。由此可知，传感器信息到达融合中心的时刻分为4种情况，针对各种情况分别进行处理：

图3 信息到达融合中心时间情形Fig.3 The situation of the time when the information arrives at the fusion center

1)情况a表示该时刻各传感器节点的信息全部准时到达融合中心，故融合中心可以正常对各传感器信息进行融合处理。

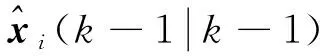
(8)

而由于当前时刻传感器i没有引入新的信息，因此，该时刻传感器i冗余向量为零向量，即

ri(k|k-1)=0

(9)

3)情况c表示融合中心收到了全部传感器的信息，但是部分传感器信息为延时信息，而此时融合中心的信息量和正常情况相同。与情况b相似，融合中心有传感器i的上一时刻信息，因此利用上一时刻信息预测处理并参与融合。但值得注意的是，当前时刻传感器i引入了新的信息，因此该时刻传感器i冗余向量应为引入信息的冗余向量，即

ri(k|k-1)=ri(k-1|k-1)

(10)

4)情况d表示融合中心接收到包括之前延时信息的全部传感器信息，且信息量比正常情况下的多。一般情况下，当增加传感器的信息时，估计误差协方差的迹有可能减小，即所利用的信息越多，估计效果越好。因此，对于当前时刻到达传感器i的全部信息可以分成两部分处理，上一时刻的延迟信息可以按照情况c处理，当前时刻信息按照情况a处理。同时,这种处理方法还有利于传感器从时间延迟情况到正常情况的平稳过渡。值得注意的是,在OWA信息融合算法中，加权矩阵的计算方式是根据滑窗内一段时间的冗余向量计算生成，故零向量的引入并不会引起求逆计算的错误。

4 仿真校验

本文以无人机空中目标为研究对象，综合使用多个不同种类传感器进行探测跟踪。以地基雷达A为融合中心，并以地基雷达A的测量坐标系为公共坐标系。采样周期为T1=1s，测距精度为300m，测角精度为0.05°，地基雷达B的坐标为(-4km,3km,0km)，两个地基雷达的采样周期为T2=3s，测距精度为300m，测角精度为0.02°，数据延迟率为0.5；空基传感器平台初始坐标为(35km,5km,6km)，运动速度为(-100m/s,60m/s,0m/s)，空基传感器采样周期为T3=6s，测距精度为100m，测角精度为0.01°，数据延迟率为0.8。假设目标在公共坐标系XOY平面内以(40km,50km,5km)为圆心，半径为20km，做角速度ω=0.0105rad/s的圆周运动，Z轴初始高度为5km，以1m/s的速度匀速下降。进行20次蒙特卡罗仿真实验，每次仿真时间为600s。目标真实运动轨迹如图4所示。

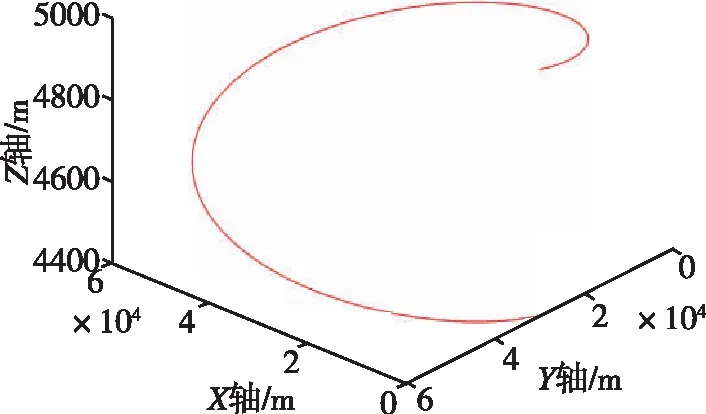
图4 目标运动形式Fig.4 The real trajectory of the target

仿真结果如图5、图6和表1所示。

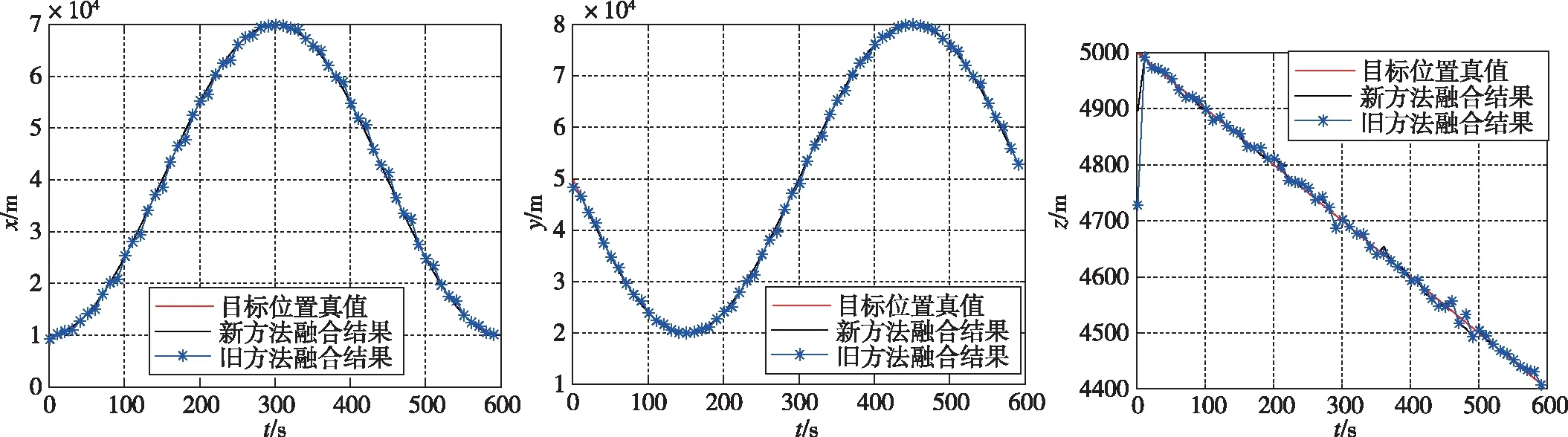
图5 目标位置估计结果Fig.5 Target position estimation result

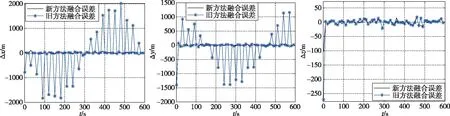
图6 目标位置估计误差Fig.6 Target position estimation error

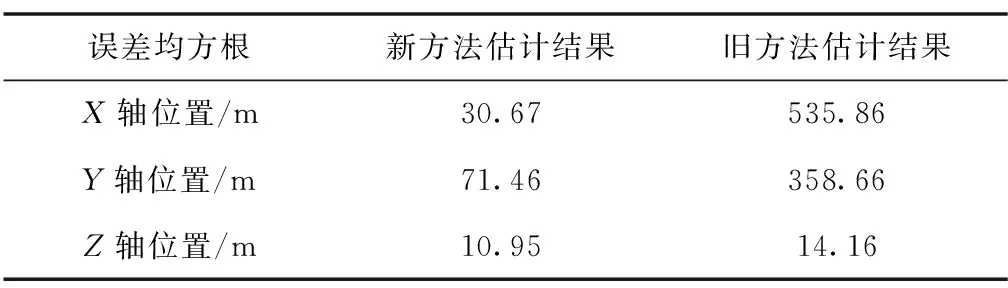
表1 目标状态估计的均方根误差

图5和图6中新方法指使用改进的尺度递归融合方法以及对传感器数据的时间延迟进行补偿配准，而旧方法指使用原尺度递归融合方法且没有对传感器的时间延迟进行配准。从仿真结果可以看出，在XOY平面内，由于目标一直机动，当传感器的数据出现延迟时会严重影响融合中心的估计结果，而使用新方法可以有效提高对目标的估计精度。而在Z轴上，目标机动较小，传感器数据延迟对融合估计的影响不大，因此两种方法的估计效果差不多，但是从目标状态的估计均方根误差来看，新方法的估计效果要好一些。从仿真结果中可以得出结论，本文研究的改进尺度递归融合算法和时间延迟配准算法可以有效解决多传感器在信息融合过程中的异步融合和时间延迟问题。

5 结 论

本文针对多传感器协同探测信息融合中的时间配准相关问题进行研究，主要解决了不同传感器采样周期不同的异步融合问题和因通信等问题产生的时间延迟。对于多传感器采样率不同而出现的异步融合问题，本文根据多尺度系统理论，设计了基于OWA信息融合算法的多尺度状态融合估计算法。之后又针对多传感器融合中的时间延迟问题，分析了时间延迟过程中的各种情形，利用状态预测和OWA算法中滑窗预存储信息的特点解决了这一问题。文中给出的仿真实例说明了该方法的有效性。