Zirlo锆合金高温变形行为及本构关系
2022-03-20宋广胜牛嘉维宋鸿武张士宏邓思瀛
宋广胜,牛嘉维,宋鸿武,张士宏,邓思瀛
(1 沈阳航空航天大学 材料科学与工程学院,沈阳 110036;2 中国科学院金属研究所 师昌绪先进材料创新中心,沈阳 110016)
锆及锆合金由于其较小的中子吸收截面,具有优异的核性能,近年来引起了人们的广泛关注[1]。因其抗蒸汽腐蚀性能优异,并具有良好的加工成形性能、焊接性能和力学性能,被广泛用于制备压水堆核电站中的燃料包壳管以及定位格架[2]。由于工业纯锆内部含有较多Hf元素杂质,其强度和抗蚀性能大大减弱。为了满足核电领域对材料的要求,通常需要对锆进行合金化处理[3]。锆合金板材主要用于化工、制药等行业中耐腐蚀设备的制造,其间需要对板材进行弯曲等塑性变形,建立能够描述在不同变形条件下力学行为的锆合金本构模型,对锆合金轧制板材的轧制工艺及其塑性加工有重要的指导意义。目前国内外对锆合金的热变形行为及本构关系已开展了相关研究,肖大武等[4]基于位错动力学理论,建立了纯锆的本构模型并考虑孪晶演化对模型的影响。董艺伟[5]对Zr92Ti8合金进行了Arrhenius本构模型及人工神经网络模型的建立。Saxena等[6]和Saboori等[7]分别对Zr-2.5Nb-0.5Cu及Zr-1Nb合金进行了传统Arrhenius本构模型的建立。
传统Arrhenius模型作为经典的本构模型,在不同材料的本构模型构建中得到了广泛的应用[8-9],但由于Arrhenius本构模型基本形式中仅考虑了不同温度及应变速率对流变应力的影响,而没有应变这个参数,因此仅适用于流变应力达到峰值后保持不变的动态回复型应力-应变曲线。而对于流变应力随应变的增加而变化的曲线会产生偏差,且随着应变的增加偏差值越来越大。万鹏等[10]和张施琦等[11]分别对Ti-2.7Cu合金及22MnB5Nb钢进行了基于应变补偿Arrhenius本构模型的构建,并取得了良好的效果,模型可以较准确地预测各变形条件下的应力值。但刘强等[12]使用同样的方法对Ti-6Al-4V-0.1Ru合金构建应变补偿本构模型获得的效果并不好,预测应力值与实验值之间产生了较大的偏差。这说明基于应变补偿Arrhenius本构模型仍有其局限性。
Zirlo合金为Zr-Sn-Nb系合金,其耐腐蚀性能优良,显著降低核燃料循环费用,因而被广泛应用于核工业中,其相关的热变形行为及本构模型的研究鲜有报道。本工作对Zirlo锆合金进行热压缩变形实验,研究Zirlo锆合金高温流变应力行为并研究其本构关系。对合金建立两种本构模型,分别为基于应变补偿Arrhenius的本构模型及基于结合Estrin-Mecking加工硬化模型和唯象型的软化模型的分段本构模型,对两种本构模型的精度进行了分析对比,为Zirlo锆合金热加工提供理论依据。
1 实验材料与方法
实验材料为Zirlo锆合金轧制板材,板材尺寸为450 mm×240 mm×19 mm,其主要化学成分(质量分数/%)为:Sn 1.0,Nb 1.0,Fe 0.1,Zr为余量。热压缩实验在Gleeble-3800型热模拟试验机上进行,压缩试样的尺寸为φ10 mm×15 mm,试样的轴向与板材的法向一致,压缩变形前,采用砂纸打磨试样两端并覆盖石墨片以减少摩擦对实验的影响。以10 ℃/s的升温速率加热到系统设定的变形温度(550~700 ℃,温度间隔为50 ℃),并保温300 s使试样温度均匀化,然后以不同的应变速率(0.01,0.1,1,10 s-1)进行单向等温恒应变速率的热压缩变形,最大压缩量为70%(真应变1.2)。试样压缩结束后,对试样喷水冷却并由设备系统自动处理并保存相关实验数据,同时绘制真应力-真应变曲线,以表征Zirlo锆合金的热变形行为。采用EBSD技术对变形试样进行组织观察,在EBSD实验中,试样依次经历研磨、机械抛光和电解抛光,电解液为高氯酸和酒精体积比为1∶9的溶液,电解抛光参数为-40 ℃下以30 V电压电解3 min。
2 结果与分析
2.1 真应力-真应变曲线分析
图1为Zirlo合金经过温度修正后的真应力-真应变曲线,从图中可知,Zirlo合金真应力-真应变曲线的应力随温度的升高和应变速率的降低而降低,应变速率越低流变应力减小速度越快,即Zirlo合金在低应变速率下流变应力具有更强的温度敏感性。且在不同温度及应变速率下的应力-应变曲线呈现了3种不同的特征。应变速率为0.01,0.1 s-1的曲线为动态再结晶型曲线,合金在变形初始阶段受加工硬化的影响,应力随应变的增加而快速增加至峰值应力,此时加工硬化与软化作用达到平衡,随后由于动态再结晶软化和加工硬化的共同作用,使得应力随应变的增加而缓慢下降。由于在热压缩变形过程中,合金在变形初期发生动态回复和动态再结晶较迟,主要表现为加工硬化,此时晶粒内部积累的畸变能逐渐增大,位错不断缠结,表现为应力随应变量的增加而大幅上升;当应变增加到一定程度后达到峰值应力,此时动态回复及动态再结晶导致的动态软化速率开始大于加工硬化速率,表现为应力随应变的增加而缓慢下降。

图1 Zirlo合金在不同温度下压缩的真应力-真应变曲线(a)T=550 ℃;(b)T=600 ℃;(c)T=650 ℃;(d)T=700 ℃Fig.1 True stress-true strain curves of Zirlo alloy compressed at different temperatures(a)T=550 ℃;(b)T=600 ℃;(c)T=650 ℃;(d)T=700 ℃
较高温(650 ℃)下应变速率为1 s-1及10 s-1的曲线为动态回复型曲线,曲线上的应力达到峰值后趋向于平稳,此时动态回复及少量动态再结晶发生的软化作用与加工硬化达到了平衡。而高温(700 ℃)下应变速率为1 s-1及10 s-1的曲线表现为由动态回复型曲线转变为动态再结晶型曲线,这是由于温度的升高促使了动态再结晶的发生。
在较低温(550,600 ℃)下应变速率为1 s-1及10 s-1的压缩过程中,动态回复发生的软化作用与加工硬化达到平衡后,随着应变的累积,动态回复产生的软化作用不足以抵消加工硬化,曲线的应力又开始缓慢上升。这是因为在热压缩变形过程中,较低的温度和较高的变形速率抑制了动态回复和动态再结晶的发生。因为压缩速率提高,合金内部产生大量的位错,增加位错相互缠结的概率,从而增大位错运动过程中所受阻力,在此条件下,试样发生热压缩变形需要较大的流变应力,且变形量越大,位错缠结概率越大,缠结越复杂,变形所需的流变应力也就越大。温度降低,合金内部原子的活性减小,原子能量降低,运动速率降低,减少了原子之间碰撞的概率,从而抑制动态回复和动态再结晶的发生[13]。因而低温高应变速率曲线仍呈现加工硬化型曲线特征。
图2显示了不同变形条件下Zirlo合金压缩试样心部变形组织,从图中可以看出有大量再结晶晶粒沿晶界分布。图2(a)和2(c)对比表明,在变形温度相同条件下,应变速率的降低将提高再结晶程度,同样图2(a)和2(b)的对比结果显示,在应变速率相同条件下,再结晶程度随变形温度升高而提高,这与上述力学性能曲线的行为表征一致。图2(c)中显示在700 ℃,1 s-1变形条件下的试样仅发生少量的动态再结晶,因此该变形条件下是以动态回复为主而动态再结晶为辅进行的软化过程,这与前文所述相符,表明在该变形条件下曲线正在由动态回复型向动态再结晶型转变。

图2 不同变形条件下压缩试样晶粒取向图Fig.2 Grain micrographics of the samples compressed under different deformation conditions
2.2 峰值应力模型的构建
由图1所示真应力-真应变曲线,取加工硬化及软化作用首次平衡点为峰值应力点,采用等温热变形条件下的Arrhenius流变应力本构方程[14]构建峰值应力模型:

(1)
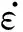
式(1)中的应力函数F(σ)根据应力水平高低,具有以下两种形式:
F(σ)=|σn1| (α|σ|<0.8)
(2)
F(σ)=exp(β|σ|) (α|σ|>1.2)
(3)
式中:α,n1和β均为材料相关常数,其中,α=β/n1。式(2)适用于高温低应变速率条件,式(3)适用于低温高应变速率条件。
对于任意应力水平,F(σ)也可以表示为基本形式:
F(σ)=sinh(α|σ|)n
(4)
式中:n为材料相关常数;sinh为双曲正弦函数,其表达式为:
(5)
分别将式(2)~(4)代入式(1),并对等式两边求对数可以得到:
(6)
(7)

(8)
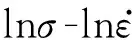

图3 峰值应力与应变速率的关系Fig.3 Relationship between peak stress and strain
式(8)可变换为:
(9)

(10)
Q=Rn{dln[sinhασ]/d(1/T)}
(11)

(12)


图4 峰值应力与应变速率及温度的关系Fig.4 Relationship between peak stress and strain rate, temperature
根据式(9)将图4(a)所得各直线斜率取倒数的平均值可得n=10.81344,图4(b)所得斜率的平均值代入式(11)可得Q=309.81 kJ/mol,并将n值与图3(b)所得截距代入式(12),并对所得lnA求平均值可得lnA=39.135,则A=e39.135=9.911×1016。
将所得参数A,α,n,Q代入式(1),即获得Zirlo合金峰值应力模型:
exp[-309810/(8.314T)]
(13)
2.3 Zirlo合金应变补偿模型的构建及分析
为在传统本构模型上加入应变补偿以进行进一步优化,在0.2~1.0应变范围内,以0.1为应变间隔分别建立了该应变下的Arrhenius流变应力本构模型,求取过程与上文相同,各应变下材料参数如表1所示。
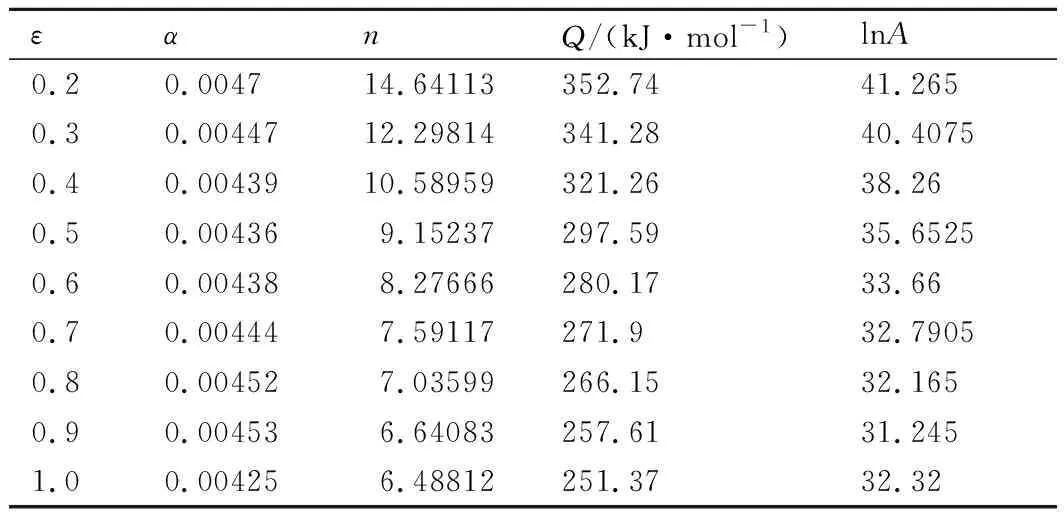
表1 不同应变下的材料参数Table 1 Material parameters at different strains
采用多项式拟合的方法建立材料参数与应变之间的函数关系,由于其材料参数α,n,Q和lnA与真应变ε之间的关系应用五次多项式拟合效果最好,其相关系数R2均大于0.998,故采用五次多项式对应变补偿参数进行拟合,如图5所示。

图5 多项式拟合Zirlo合金材料参数与真应变的关系(a)α;(b)n;(c)Q;(d)lnAFig.5 Polynomial fitting of the relationship between material parameters and true strain of Zirlo alloy(a)α;(b)n;(c)Q;(d)lnA
其所确定的函数表达式如下:
(14)
为确定加入应变补偿的改进型Arrhenius流变应力本构模型准确度,取不同变形条件下Zirlo合金在应变为0.2~1.0范围内的流动应力实测值与预测值,建立误差图如图6所示。从误差图可以看出,加入应变补偿的改进型Arrhenius流变应力本构模型大部分预测值与实测结果吻合较好,但仍有部分预测值误差大于15%,这是因为Zirlo合金在不同加工条件下应力随应变变化的趋势不同,而应变补偿通常适用于不同加工条件下应力值随应变的增加具有相同变化趋势的合金,应变补偿的改进型Arrhenius流变应力本构模型的精度稍差,此本构模型不能很好地预测锆合金应力值随应变的变化。高夏云[15]建立了与Zirlo锆合金成分近乎相同的Zr-4锆合金应变补偿本构模型,获得了相同的结果,故应采用其他方法继续建立本构模型。

图6 Zirlo合金流变应力的实测值与理论预测值误差分析Fig.6 Error analysis on measured and theoretically predicted flow stress of Zirlo alloy
2.4 Zirlo合金分段唯象本构模型的构建及分析
宋鸿武[16]采用结合Estrin-Mecking[17]提出的基于位错密度演化加工硬化模型和唯象型的软化模型的方式,建立唯象型分段本构模型并对高温合金流变曲线进行了很好的预测,故本工作对Zirlo合金使用此方法进行本构模型的构建:
在Estrin-Mecking的加工硬化模型中,加工硬化阶段的流动应力σwh同平均位错密度ρ之间关系为:
(15)
式中:σ0为材料的屈服应力,MPa;G为剪切模量,MPa;b为柏氏矢量;ρ为位错密度,cm-2。
加工过程中的位错密度演化可表示为:
(16)
式中:k1为材料常数,与位错的平均自由程有关;k2是关于温度和应变速率的函数,与位错的重排或消失有关。
材料的加工硬化速率为:
(17)
联立式(15)~(17)可得:
σwhθ=k′-k″σ2
(18)
式中:k′及k″均为材料常数。
对式(18)进行积分,可得:
(19)

软化阶段采用唯象型的软化模型来描述这种流动软化现象,定义流动应力软化分数Xsoft[18]满足Avrami形式[19]的方程:
(20)
式中:σst为最终的稳态流动应力,MPa;k与n为材料常数;εp为峰值应变(加工硬化与软化作用首次平衡时的应变)。
由式(20)可得:
σ=σwh-(σwh-σst)Xsoft
(21)
将σwh的表达式(19)及Xsoft的表达式(20)代入式(21),即可得到综合考虑加工硬化和流动软化的最终本构模型为:
(22)
根据图1所示的真应力-真应变曲线,利用式(22)进行非线性拟合,即可确定式(22)中各参数值。拟合结果表明:参数σ0,β,k及n在不同变形条件下均为常数,其取值如表2所示。

表2 拟合得到的Zirlo合金材料常数Table 2 Zirlo alloy material constants obtained by fitting

表3 不同条件下的理想饱和应力、稳态流动应力及峰值应变Table and εp under different conditions


(23)
对理想饱和应力,稳态流动应力及峰值应变等参数进一步研究可发现其与lnZ存在函数关系,如图7所示。
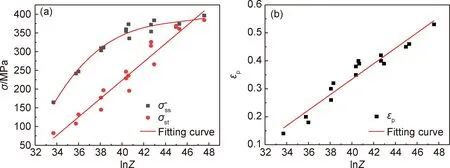
图7 理想饱和应力、稳态流动应力及峰值应变与lnZ之间的关系Fig.7 Relationship between and lnZ
15.02103(lnZ)2+0.11012(lnZ)3
(24)
σst=-756.19163+24.4901lnZ
(25)
εp=-0.77174+0.02765lnZ
(26)
利用所建立的本构模型(即式(22)),采用表2及表3中的参数值对Zirlo合金不同变形条件下的流动应力进行了预测,模型预测值同实验值的对比如图8所示,图中散点为应变在0.1~1.2范围内且间隔为0.05的真应力预测值,实线为实验测得。
从图8可以看出,基于位错密度演化的加工硬化和唯象型的软化的方式建立的唯象型分段本构模型,可以准确地预测Zirlo合金不同热压缩变形条件下的真应力-真应变曲线。为精确地判断本构模型预测的精度,可用以下方程来计算Zirlo合金预测流变应力与实验流变应力之间的相关系数(R)和平均绝对相对误差(AARE)[20]:
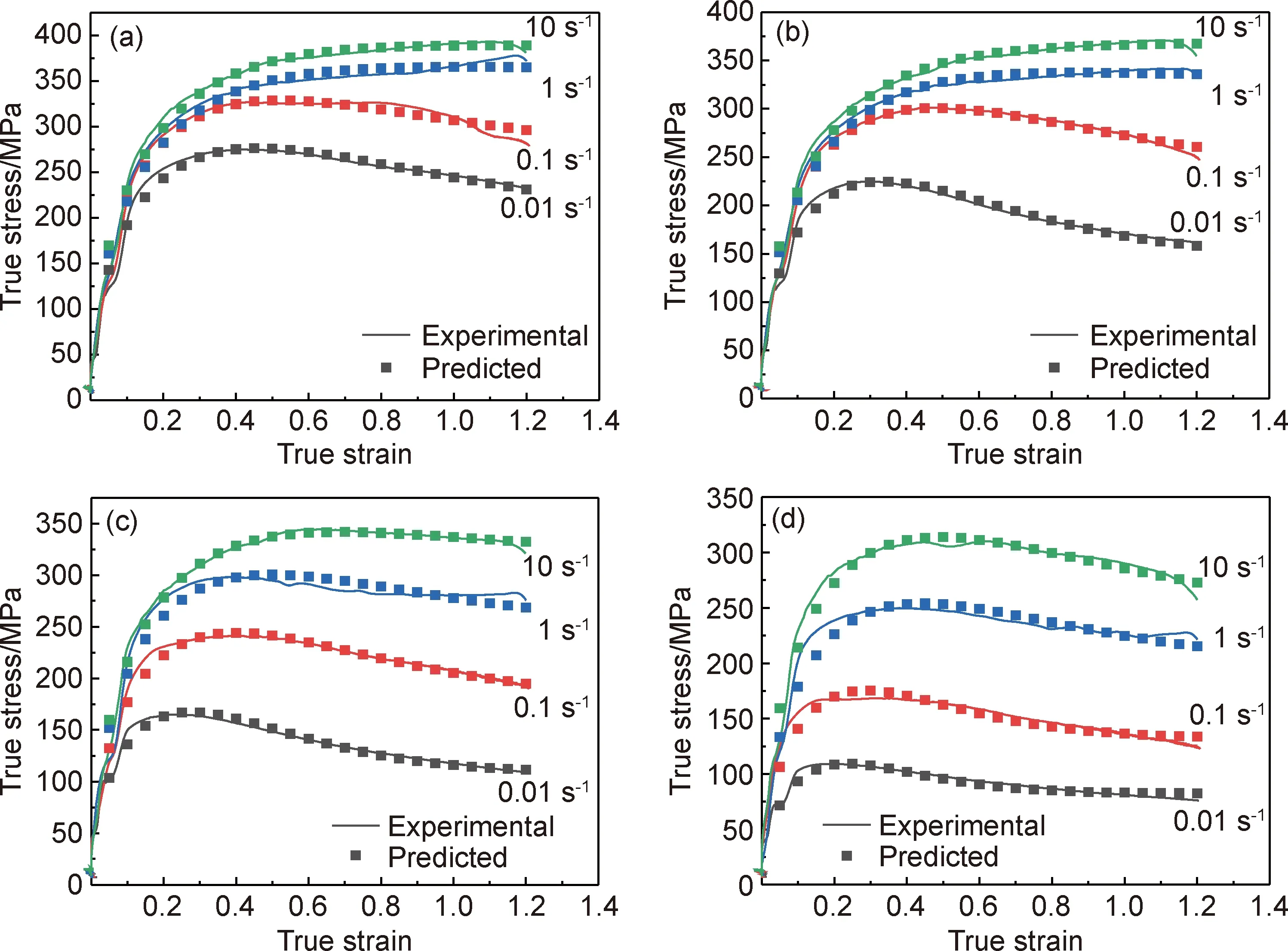
图8 应力的分段唯象型本构模型预测与实测结果(a)T=550 ℃;(b)T=600 ℃;(c)T=650 ℃;(d)T=700 ℃Fig.8 Stress predicted based on segmented phenomenological constitutive model and measured results(a)T=550 ℃;(b)T=600 ℃;(c)T=650 ℃;(d)T=700 ℃
(27)
(28)

由表4可以看出,唯象型分段本构模型对Zirlo合金真应力-真应变曲线的预测具有很高的准确度,其相对平均绝对误差最大值不超过3%,具有97%以上的准确率,可以很好地预测其流变应力曲线,且此本构方程具有良好的拓展性,可以预测当合金后续变形(真应变大于1.2)情况下的应力值,图9为700 ℃下压缩过程中应力-应变关系的实测及采用本构模型预测的结果,散点为应力-应变关系实测值,实线为由本构模型取应变间隔为0.01而获得的结果。
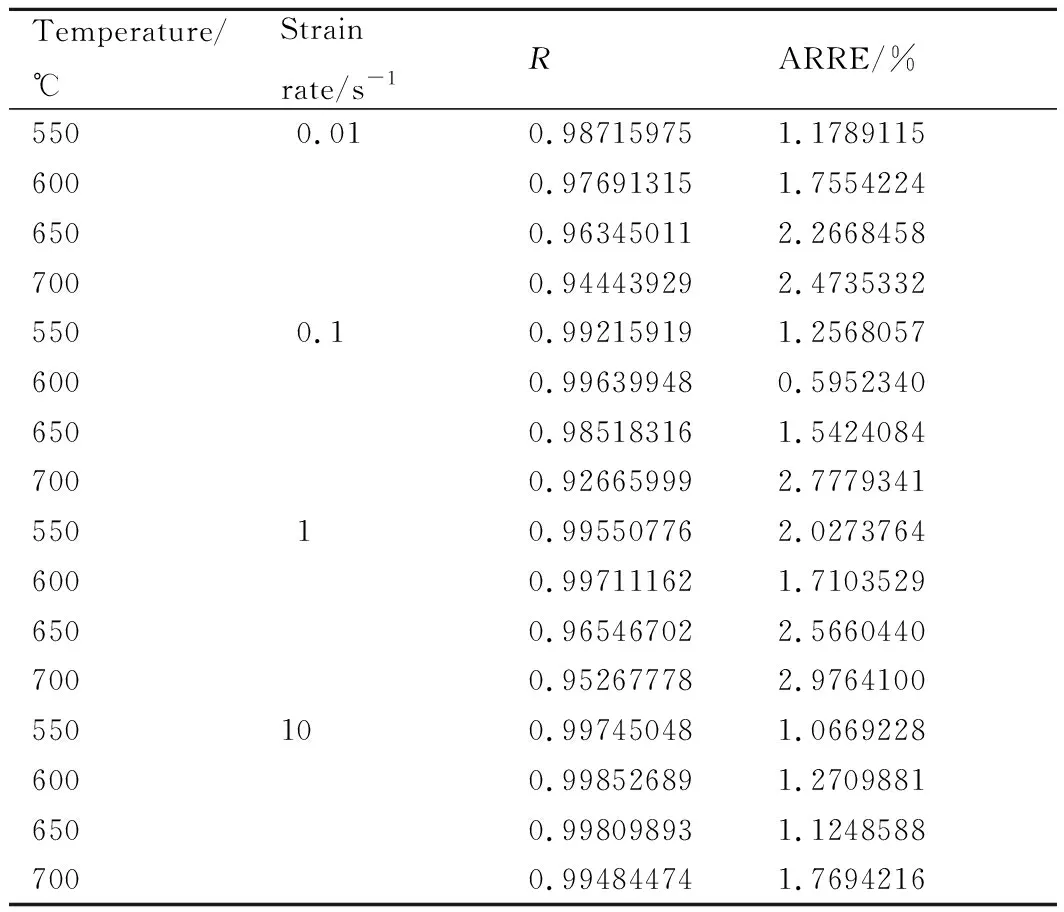
表4 各变形条件下的相关系数和平均绝对相对误差Table 4 R and AARE under various deformation conditions
唯象型分段本构模型可在已知Zirlo合金的变形温度及应变速率的情况下求取Z参数,并代入式(24)~(26)求取各变形条件下的方程参数,即可获得各变形条件下(包括本实验范围外的变形条件)的本构模型,将适当间隔的应变代入本构模型,若对应变进行延拓,亦可获得合金继续变形(真应变大于1.2)的真应力-真应变曲线,可显著减少Zirlo合金热变形力学行为的实验量;且此本构模型可以通过二次开发代入Deform等模拟软件建立材料库进行轧制等变形行为的模拟[16],有利于提高模拟结果的精确性,对于轧制工艺的设计具有一定指导作用。
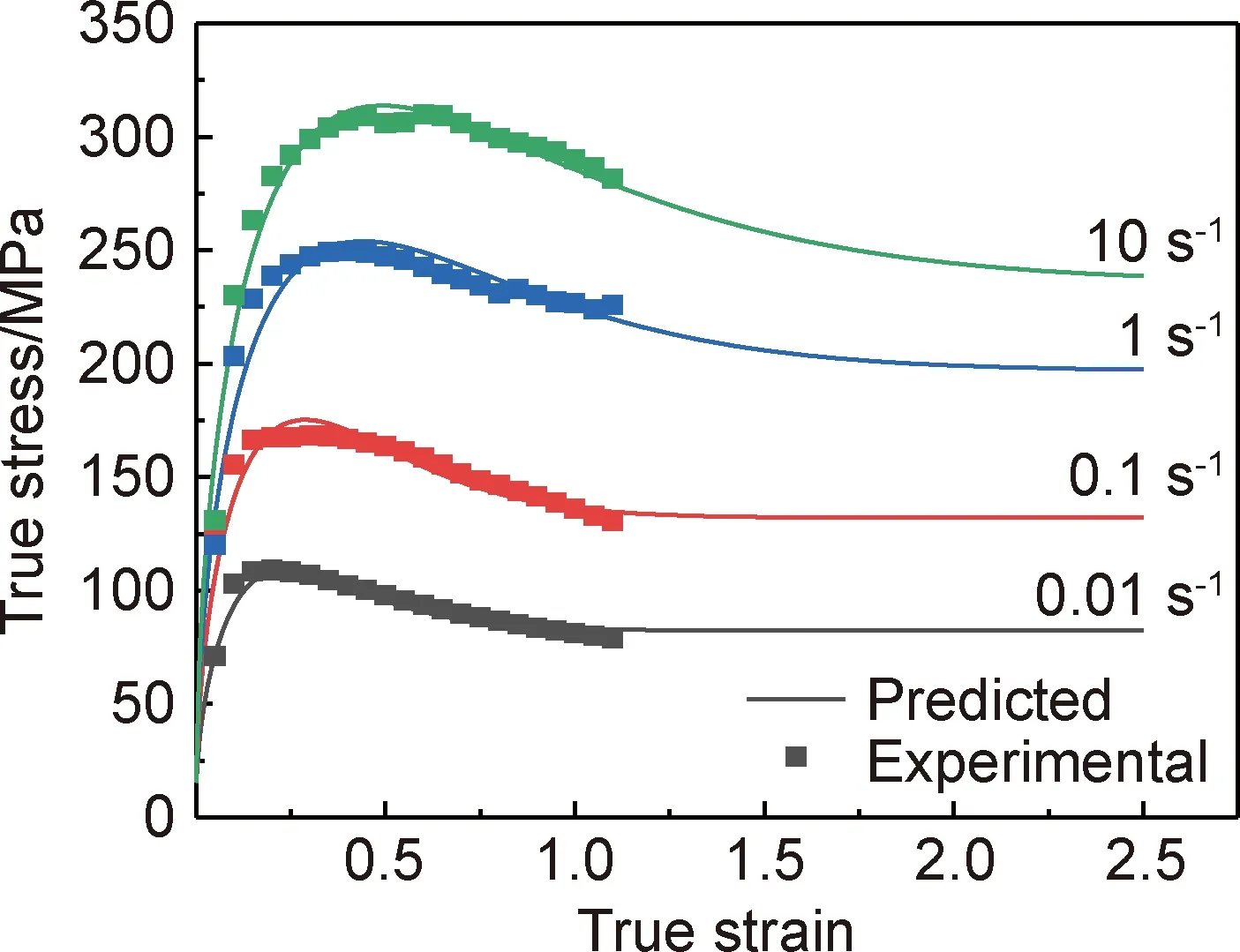
图9 700 ℃下压缩应力-应变曲线的理论预测及实验结果Fig.9 Theoretically predicted and experimental results of compression stress-strain curves at 700 ℃
因此,与基于应变补偿的改进型Arrhenius本构模型相比,唯象型分段本构模型具有准确度高,延拓性好,参数少计算简便,可根据其参数值初步判断是否发生动态再结晶及曲线类型的优点,可预测实验范围(温度,应变速率,变形量)外的真应力-真应变曲线,并可用于轧制等变形行为的模拟,具有良好的使用价值。
3 结论
(1)Zirlo合金的流变应力随着温度的升高和应变速率的降低而减小,且应变速率越低流变应力减小速度越快,即Zirlo合金在低应变速率下流变应力具有更强的温度敏感性。在温度为550~700 ℃,应变速率为0.01~10 s-1的变形条件下分别呈现加工硬化、动态回复、动态再结晶特征曲线,随着温度的升高与应变速率的降低,合金的动态回复及动态再结晶作用加强,使得合金的变形软化作用加强,由加工硬化型向动态回复型及动态再结晶型的曲线转变。
(2)建立了Zirlo合金的峰值应力模型,并在Arrhenius本构模型的基础上,使用对应变与模型参数进行多元线性拟合的方法建立了材料参数α,Q,n及lnA与应变之间的多项式函数关系,得到了基于应变补偿的Arrhenius本构模型,此模型可以预测各应变下的流变应力值,但有少部分预测误差大于15%,此本构模型不适合预测随应变的增加而应力值变化趋势不同的合金(如Zirlo合金)。
(3)采用Estrin-Mecking提出的基于位错密度演化加工硬化和唯象型的软化的方式建立唯象型分段本构模型。此模型相对平均绝对误差最大值不超过3%,具有97%以上的准确率,可以很好地预测Zirlo合金的流变应力曲线。相对于基于应变补偿的Arrhenius本构模型,唯象型分段本构模型具有准确度高、拓展性好、参数少计算简便的优点;并可根据参数初步判断是否发生动态再结晶及曲线类型,可预测实验范围(温度,应变速率,变形量)外的真应力-真应变曲线以减少Zirlo合金热变形力学行为实验量的优点,并可用于轧制等变形行为的模拟,具有良好的使用价值。
