计算辐射噪声的面声源和点声源结合方法
2021-04-08刘宝胡金华程广利
刘宝, 胡金华, 程广利
(海军工程大学 电子工程学院, 湖北 武汉 430033)
0 引言
求解结构的声辐射特性是声学界普遍关注的问题,在解析法的基础上,对不规则结构通常采用有限元法(FEM)[1-2],边界元法(BEM)[3-4]计算。FEM在分析结构声振特性时,需要对结构和三维流体介质进行单元离散和变量插值,计算量庞大。相对于FEM,BEM具有自动降低求解维度和适用于无限域的优点。但是采用BEM计算时,需要处理奇异性积分问题和对应内部Dirichlet特征频率处解的唯一性问题,虽然理论上可以采用CHIEF法[5]、Burton-Miller法[6]等获得全波数范围内唯一的解,但无疑增加了计算的复杂性和存储空间,降低了求解效率。
为此,19世纪90年代,Koopmann等[7-9]提出了采用简单源匹配的虚拟声源方法。作为边界元的一种有效的替代方法,将结构产生的声场看作是由置于该辐射体内部有限多个虚拟点声源产生的声场叠加,虚拟声源的源强可以通过匹配结构表面上若干点的法向速度获得。进一步利用源强可以直接求解声场任一点声压、辐射声功率等声学参数。后来,Koopmann等开发了采用虚拟声源计算的软件POWER,并出版了相关专著[10]。Benthien等[11]指出:虚拟声源所在区域与结构表面不重合,因而不需要处理奇异性问题,并且可提高计算效率。实际应用中为了计算上简单方便,一般将点声源布置在一个虚拟表面上。然而Jeans等[12]和Wilton等[13]的研究表明,正是由于采用了一个封闭曲面作为虚拟声源的配置区域,导致了在关于虚拟面内部Dirichlet问题的特征频率处,解非唯一。为此他们提出了采用复数形式的Burton-Miller型组合层势法,该类方法虽然解决了特征频率处解的唯一性问题,但是相对于单独采用单层势或双层势,其计算时间增加了50%左右。
为了保证全波数域内解唯一,Xiang等[14]提出了基于复数矢径的虚拟声源方法,他们将计算半径改为复数,相当于在结构动力系统中加入阻尼,则在整个波数范围内保证了解的唯一性。运算该技术,向宇等[15]求解了空腔、空穴等二维结构的声振耦合问题,并进一步求解了三维轴对称空穴的声辐射问题,结果表明:基于复数矢径的虚拟声源方法具有很高的计算精度。夏雪宝等[16]根据波叠加原理,研究了声压、声源强度和表面法向振速之间的关系,推导了结构声辐射阻矩阵,并进一步提出了附加源虚拟声源方法,在单极子虚拟声源法的基础上,在虚拟面内部添加一定数量的附加源,获得声场全波数域内声辐射特性的唯一解,案例表明其计算效率和精度都优于Burton-Miller型组合层势法的结果[17]。文献[18]则采用面声源代替点声源构造结构外声场,以二维脉动和摆动空穴为例,验证了采用面声源作为虚拟声源计算的精确性,同时面声源对位置的灵敏度小于点声源。
在应用虚拟声源方法求解声学参量时,虚拟声源数目和位置的选择对于求解的精度和效率有很大影响。采用虚拟声源方法计算时,在声辐射阻抗矩阵非对角线上元素占优的情况下[19],容易造成声辐射阻抗矩阵病态,所计算的结果存在较大的误差。根据灵敏度分析,当结构内部虚拟声源位置不变时,结构表面振速分布是声辐射参数的敏感变量,即振速分布的微小扰动可能使得虚拟声源方法的计算结果产生较大误差。文献[8]针对不同表面振速分布的柱状声辐射体,采用虚拟声源方法进行了数值计算后指出,虚拟声源方法的误差与振速分布、波数、表面节点、虚拟声源位置和个数都有关系。因此,为了保证求解的精度,需要针对不同结构的表面振速分布,调整虚拟声源的个数和位置。
为了使得声辐射阻抗矩阵对角线上元素占优,Koopmann等[9]由Borgiotti等[20]采用奇异值分解方法,建立结构表面振速和远场声压,将声辐射阻抗矩阵接近于0的奇异值截断,形成新的声辐射阻抗矩阵,结果表明,采用新的声辐射阻抗矩阵计算的结果在精度上高于原声辐射阻抗矩阵的结果。Zellers[21]则是利用无网格技术,将单极子、偶极子、三极子置于结构离散单元的中心处,获得了自辐射阻抗的解析表达式,用来替代声辐射阻抗对角线上的元素,计算结果表明,该方法可以保证对角线上的元素占优,且在低频时可以取得较好的计算精度。上述工作针对声辐射阻抗矩阵,进行了不同程度的改进,在一定程度上减小了计算误差,但没有考虑同样会导致计算误差的虚拟声源位置因素。Hwang[22]的研究表明,虚拟声源所在面应该尽量与结构表面共形,并且在理论上给出了虚拟面与结构实际表面的最小距离,但没有给出最大距离的限制。因此当虚拟面与结构实际表面的距离较大时,计算的结果仍可能不精确。Gounot等[23]、Pavic[24]则采用遗传算法搜索一定范围的虚拟空间,将虚拟声源在结构表面的振速与结构表面实际的振速相比较确定虚拟声源的位置。当虚拟声源数量庞大时,计算效率低,且搜索的虚拟声源位置有可能为局部最优位置。陈鸿洋等[25]以水下带帽圆柱壳为对象,由声场匹配搜索等效声源分布,获得最小二乘意义下的最优等效源位置,所得结果在较宽频段内具有较好的适应性,且适用于半无限大声场。Wu等[26]提出了根据体积速度匹配原则确定虚拟声源位置的方法,研究表明当虚拟声源位于优化位置时,在中高频上也可以保证良好的计算精度。商德江等[27]将波叠加原理、简正波理论和多物理场有限元方法相结合,提出了一种浅海信道下弹性结构声辐射快速预报的联合算法,并从数值法结果和解析解结果两方面验证了联合算法的准确性和可靠性。
本文根据波叠加原理,利用面声源和点声源作为非共面的虚拟声源,搜索与边界条件相匹配的真实声压与结构表面振速,提出了一种保证全频域解唯一的虚拟声源方法。该方法在结构内部同时布置虚拟面声源和点声源离散声场,面声源位于结构内部一个与结构边界共形的表面,用其匹配结构表面的声压与振速,点声源则位于虚拟表面内部,由于与虚拟表面不共面,因而可以保证解在特征频率处的唯一性。文中以脉动球源和横向振动球源为例,首先比较了点声源和面声源作为虚拟声源计算的精确性,进一步将本文所提方法与解析法、虚拟点声源法、虚拟面声源法相比较,说明该方法的优点。
1 波叠加原理
结构产生的声场可以看作是由结构内部空间中声源辐射声场的叠加,此即波叠加原理。波叠加原理示意图如图1所示。
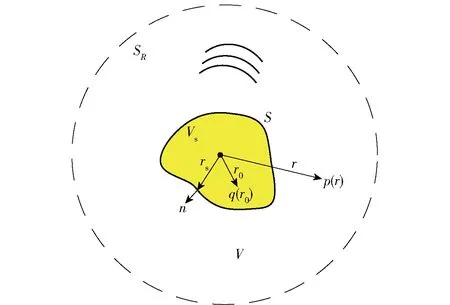
图1 波叠加原理示意图Fig.1 Schematic diagram of wave superposition principle
图1中:SR为以R为半径的球面;S为结构表面积;V为结构外空间;Vs为结构所占体积;rs为结构中心到表面一点处距离;r0为结构中心到虚拟声源所在位置处距离;n为结构外法线方向;q(r0)为r0位置处虚拟声源强度;r为结构中心到声场内一点距离;p(r)为r位置处声压。
如图1所示,场点r处的声压p(r)可以看做是由所有虚拟声源辐射声场的线性叠加,从而表示为
(1)
式中:j为虚数,j2=-1;k表示波数;ρf为介质密度;c为声速;q(r0)为虚拟声源分布在r0处的声源强度;Gk(r,r0)为自由空间的格林函数,满足
(2)
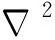
理论上可以证明(1)式与Helmholtz边界积分方程等价。根据(1)式,可以推导出虚拟点声源法和虚拟面声源法。
2 虚拟点声源法
根据波叠加原理,将结构产生的声场看作是由结构内部空间中点声源辐射产生的声场叠加。即当点声源作为虚拟声源时,q(r0)可以表示为内部有限个点声源的组合,即
(3)
式中:m为虚拟声源数目,m=1,2,3,…,M;s(rm)为对应rm位置处的虚拟声源强度。
(3)式代入(1)式可得
(4)
(4)式为单层势形式的声压计算公式。在此基础上,可以给出双层势和混合势形式的声压计算公式,分别如(5)式和(6)式所示。
(5)
(6)
式中:γ=j/k;nm表示对应于rm位置处的结构外法线方向。(4)式、(5)式、(6)式表示成矩阵形式为
p=Hs,
(7)
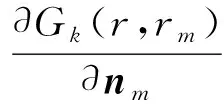
(8)
(9)
(10)
(8)式~(10)式表示成矩阵形式为
u=Us,
(11)
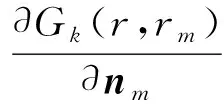
s=U-1u,
(12)
(12)式代入到(7)式中,即可求解结构表面声压为
p=HU-1u.
(13)
除了采用(13)式计算结构的表面声压外,还可以采用最小二乘法建立虚拟声源强度求解方程,进一步求解表面声压。以单层势为例进行计算,由最小二乘法原理,(8)式建立泛函形式的方差表达式如(14)式所示。
(14)
式中:F1表示泛函的方差;nrn为对应位置rn处的法线方向;vm为第m个结构表面节点位置处的振速。展开(14)式可得
(15)
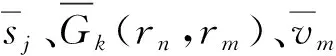
(16)
(15)式代入(16)式,可得
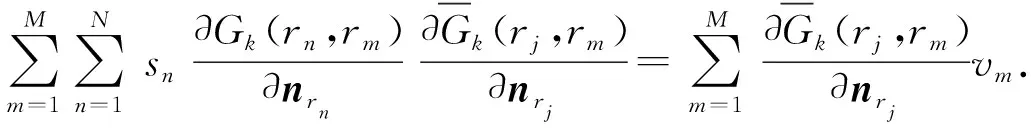
(17)
利用(17)式即可求得最小二乘意义下的虚拟声源强度,进一步求解表面振速。
3 虚拟面声源法
当虚拟声源连续分布于结构内部的某个虚拟边界面时,由波叠加基本原理,(1)式可以写为
(18)
式中:α、β分别为结构表面上一点位置和虚拟声源所在位置的符号表示。由于采用面单元作为虚拟声源,因此需要对虚拟声源强度q(β)进行变量插值,在此以二次等参单元为例,将虚拟边界面划分为Ne个单元,每个单元含有8个节点,共含有N个节点。于是单层势形式的声压计算式可以表示为
(19)
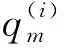
(20)
(21)
对同一个节点上的积分函数进行合并,采用Gauss积分计算,最后表示成矩阵形式如下:
p=Gq,
(22)
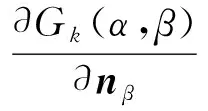
(23)
(24)
(25)
(23)式、(24)式、(25)式最终表示成矩阵形式为
u=Qq,
(26)
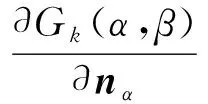
p=GQ-1u.
(27)
同样地,可以采用最小二乘法建立虚拟声源强度的求解方程。以单层势为例进行计算,由最小二乘法原理,(26)式建立泛函形式的方差表达式如(28)式所示。
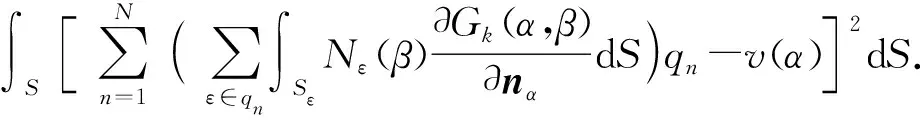
(28)
对(28)式进行展开,可得
(29)
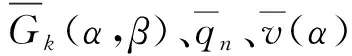
(30)
由(30)式即可计算出虚拟声源强度,进而求解结构的表面声压。在引入基虚拟点声源法和虚拟面声源法后,本文继续对比上述两种虚拟声源法的精度和计算效率。
4 不同声源类型的计算结果比较
为了比较虚拟点声源法和虚拟面声源法各自的特点,以平面圆形空穴为例,其半径为r,分别进行脉动和横向振动,其边界线速度分别为v0和v0cosθ(θ是x轴方向与横向振动方向的夹角)。以空穴中心为圆心,半径为0.7r的圆作为虚拟边界线,在虚拟边界线上等间距地选择8个节点作为点声源。同样地将该虚拟边界线离散为4个二次等参单元作为面声源,共含有8个节点,如图2所示。设速度v0=1,r=1,采用上述两种虚拟声源匹配圆形边界线上的速度,并将所得结果进行比较,图3、图4、图5分别为在频率kr=π rad/s,kr=2π rad/s,kr=3π rad/s时的结果。
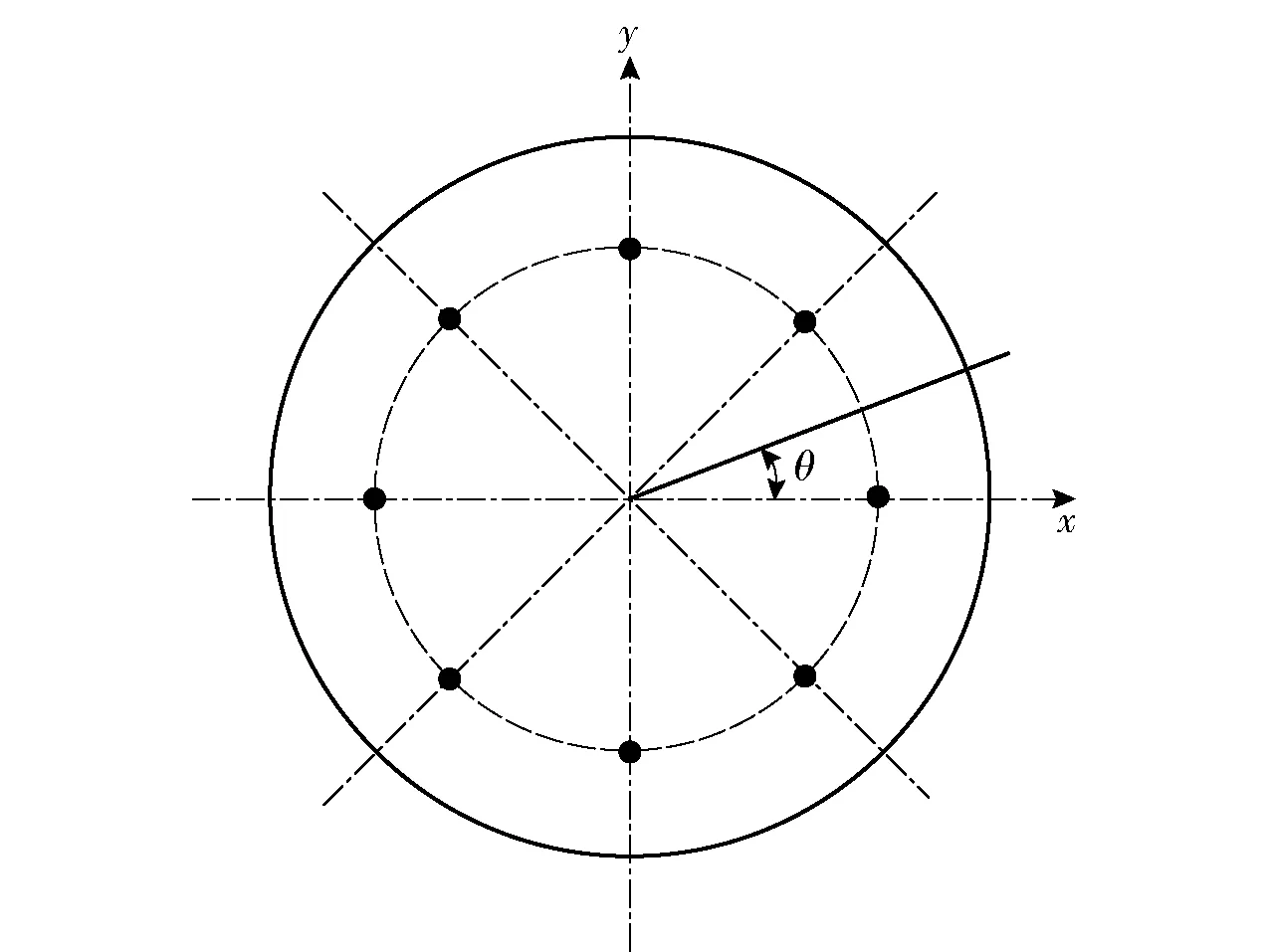
图2 虚拟声源布置模型Fig.2 Layout model of virtual sound sources

图3 kr=π rad/s时速度匹配图Fig.3 Velocity matching diagram for kr=π rad/s
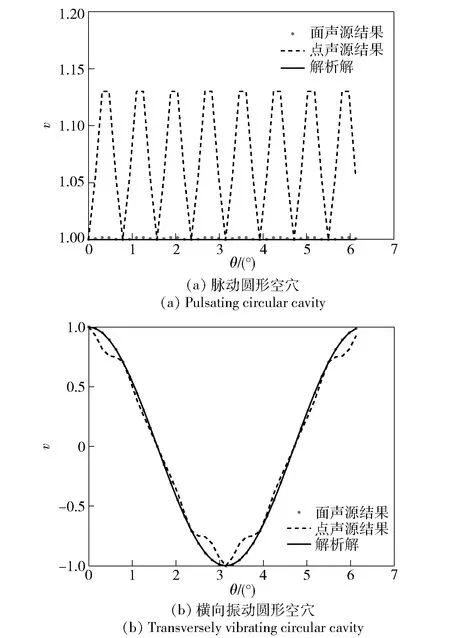
图4 kr=2π rad/s时速度匹配图Fig.4 Velocity matching diagram for kr=2π rad/s
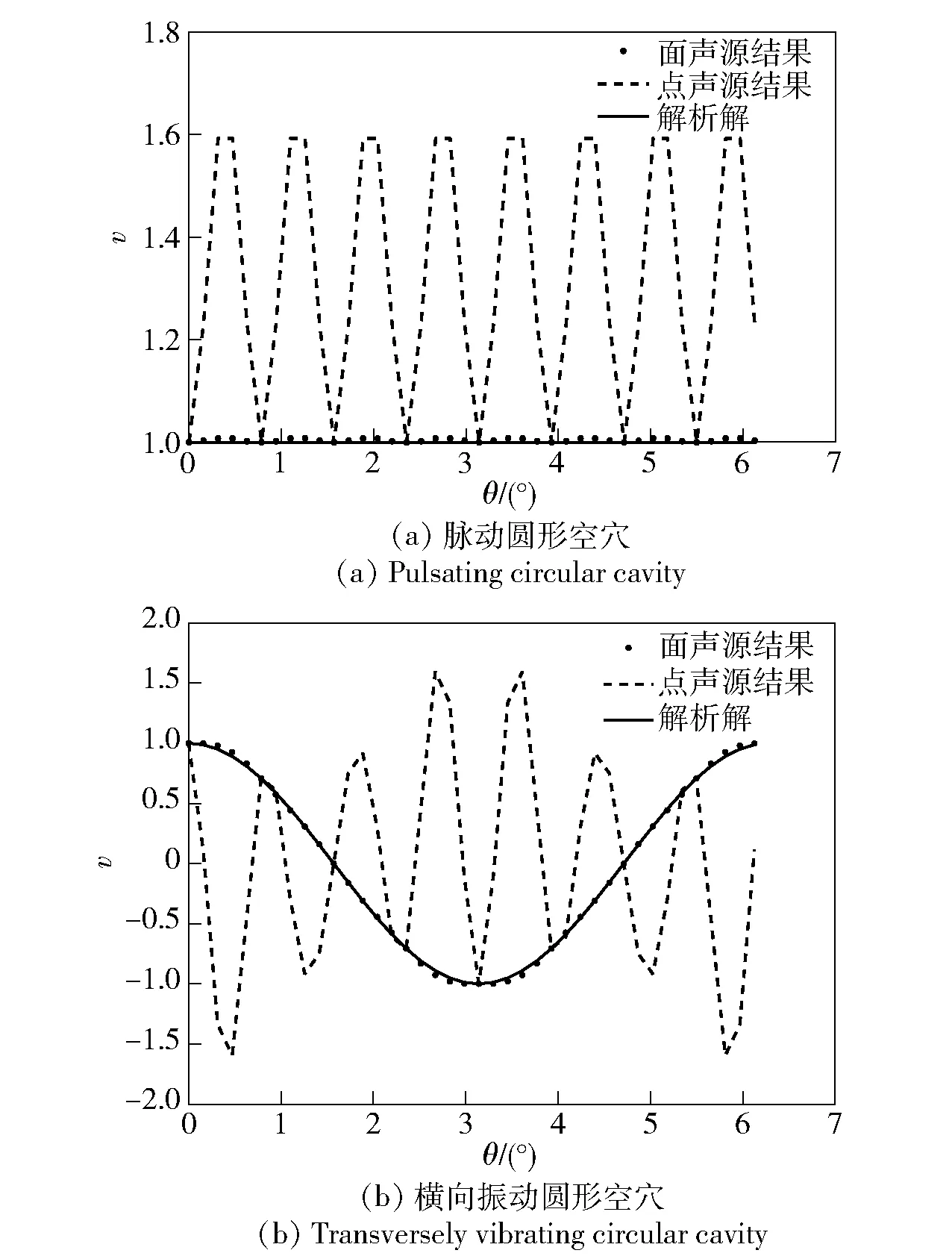
图5 kr=3π rad/s时速度匹配图Fig.5 Velocity matching diagram for kr=3π rad/s
由图3~图5可知,当频率从kr=π rad/s上升到频率kr=3π rad/s时,采用虚拟点声源法计算的误差逐渐增大,不能较好地匹配结构表面的振速。同时可以明显看出,采用虚拟面声源法的计算结果在频率kr=π rad/s、kr=2π rad/s、kr=3π rad/s时匹配的结果都很好,没有产生较大的误差。因此,虚拟面声源法计算的精度要好于虚拟点声源法的结果。当然,在计算效率上,虚拟点声源法的计算效率要比虚拟面声源法快很多,这是由于不同于虚拟面声源法需要进行积分运算,虚拟点声源法不需要积分就可以直接求解声阻抗矩阵,因此节约了大量时间。
5 面声源和点声源联合的虚拟声源法
在匹配声场中的声压与振速方面,由于虚拟面声源法的精度要高于虚拟点声源法,故采用面声源匹配声场可以获得更好地求解精度。由于面声源作为虚拟声源时通常位于同一个面上,因此在特征频率处,会出现解的唯一性问题。为此在采用虚拟面声源的基础上,在虚拟面内部布置若干虚拟点声源,用来保证解唯一。则单层势形式的声压可以表示为
(31)
该方法的基本思想是采用虚拟面声源匹配结构表面声压与振速,而点声源不与面声源共面,以保证解的唯一性,因此将该方法称为面声源和点声源相结合的虚拟声源法。考虑到点声源的存在是为了保证特征频率处的解具有唯一性,但过多虚拟点声源的存在会降低求解效率且影响计算精度。因此,要求点声源的数量尽可能少,同时在结构内具有位置合适,这也是该方法的难点所在。即如何有效地确定虚拟点声源的数目与位置。经过实际运算,当虚拟点声源数目为虚拟面声源的1/10左右且点声源的位置均匀分布在结构内部时可以较好地保证解在全波数内唯一,并且具有较高的计算精度。(31)式表示成矩阵形式为
p=[G⋮H][q⋮s].
(32)
由(31)式可以很自然地推导出振速的计算公式为
(33)
(33)式表示成矩阵形式为
v=[U⋮Q][q⋮s].
(34)
(34)式计算出的虚拟声源强度代入(32)式中,即可计算出结构的表面声压。
6 案例分析
算例1:针对无限大介质中的脉动球源,采用面声源和点声源相结合的方法计算其全频段的声辐射特性参数。设球源半径为r,结构表面法向振速为v0,介质声速为c,介质密度为ρf. 球体表面采用104个单元的8节点二次等参单元进行离散插值。以球心为原点,采用半径为0.7r的球面作为虚拟面,即放缩系数为0.7,应用相同数目的二次等参单元对该虚拟面进行离散插值,这些单元即为虚拟面源。在虚拟表面的内部均匀分布10个点作为虚拟点声源。采用Matlab编程进行计算。考虑到脉动球源表面各点理论上声压相同,以与z轴呈φ=45°(φ为z轴方向与横向振动方向的夹角)处计算的无量纲化声压为例,将本文方法结果和虚拟面声源法、虚拟点声源法的结果、解析解进行对比说明,如图6所示。
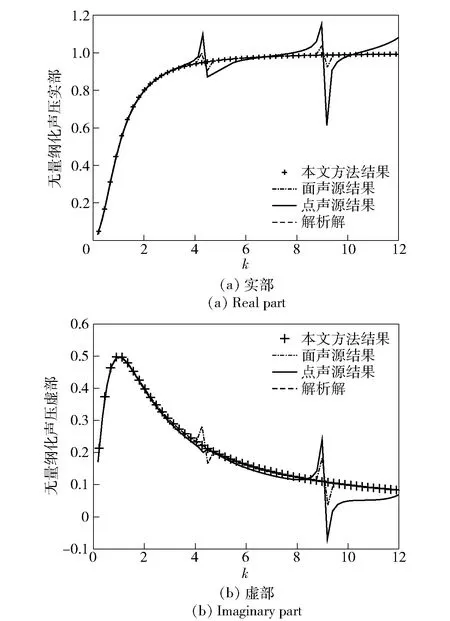
图6 脉动球源φ=45°处无量纲化声压比较图Fig.6 Comparison of dimensionless sound pressures at pulsating spherical source for φ=45°
从图6看出,点声源计算的误差随着频率的升高逐渐增大较多,在计算精度上本文方法和面声源法的结果均优于点声源法的结果。当频率接近关于虚拟面内部Dirichlet问题处的特征频率时,即kr=4.48, 8.97时,采用点声源法和面声源法的计算结果偏离解析解较大,说明虚拟点声源法和面声源法均不能保证对应特征频率处声辐射解的唯一性。采用面声源和点声源相结合的方法计算时,所得结果的实部和虚部与解析解在全部频域内吻合得很好,整体上与解析解一致,不会产生较大的偏差,说明该方法具有很好的计算精度。
算例2:针对无限大介质中的横向振动球源,采用面声源和点声源相结合的虚拟声源法计算其全频段的声辐射特性参数。设球源半径为r,表面振速可以表示为v0cosφ. 横向振动球体和虚拟声源表面离散单元的数量与离散形式和脉动球源相同。以与z轴呈φ=45°、φ=90°、φ=135°处计算的无量纲化声压和虚拟面声源法、虚拟点源法的结果、解析解进行对比说明,如图7~图9所示。
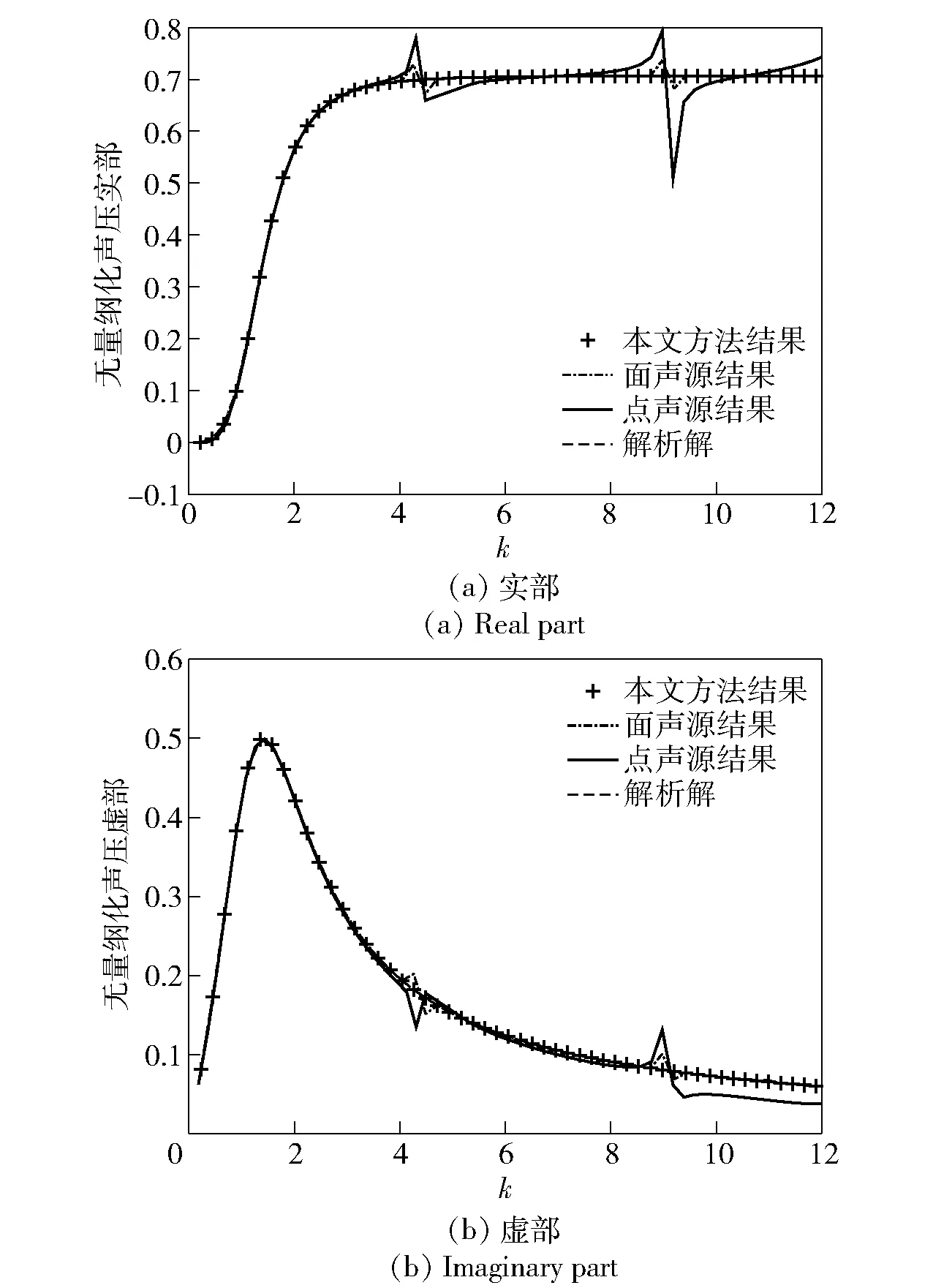
图7 横向振动球源φ=45°处无量纲化声压比较图Fig.7 Comparison of dimensionless sound pressures at laterally oscillating spherical source for φ=45°
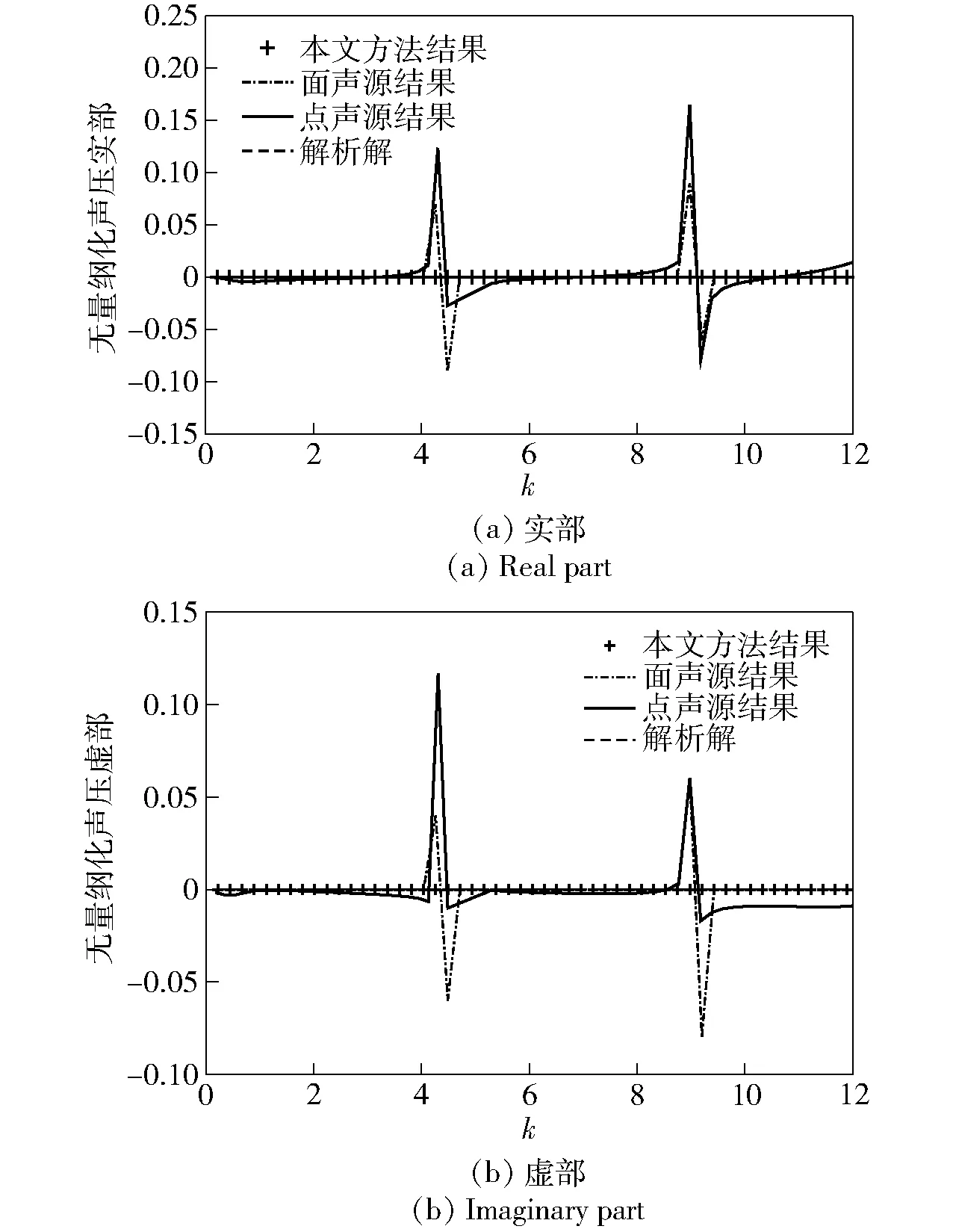
图8 横向振动球源φ=90°处无量纲化声压比较图Fig.8 Comparison of dimensionless sound pressures at laterally oscillating spherical source for φ=90°
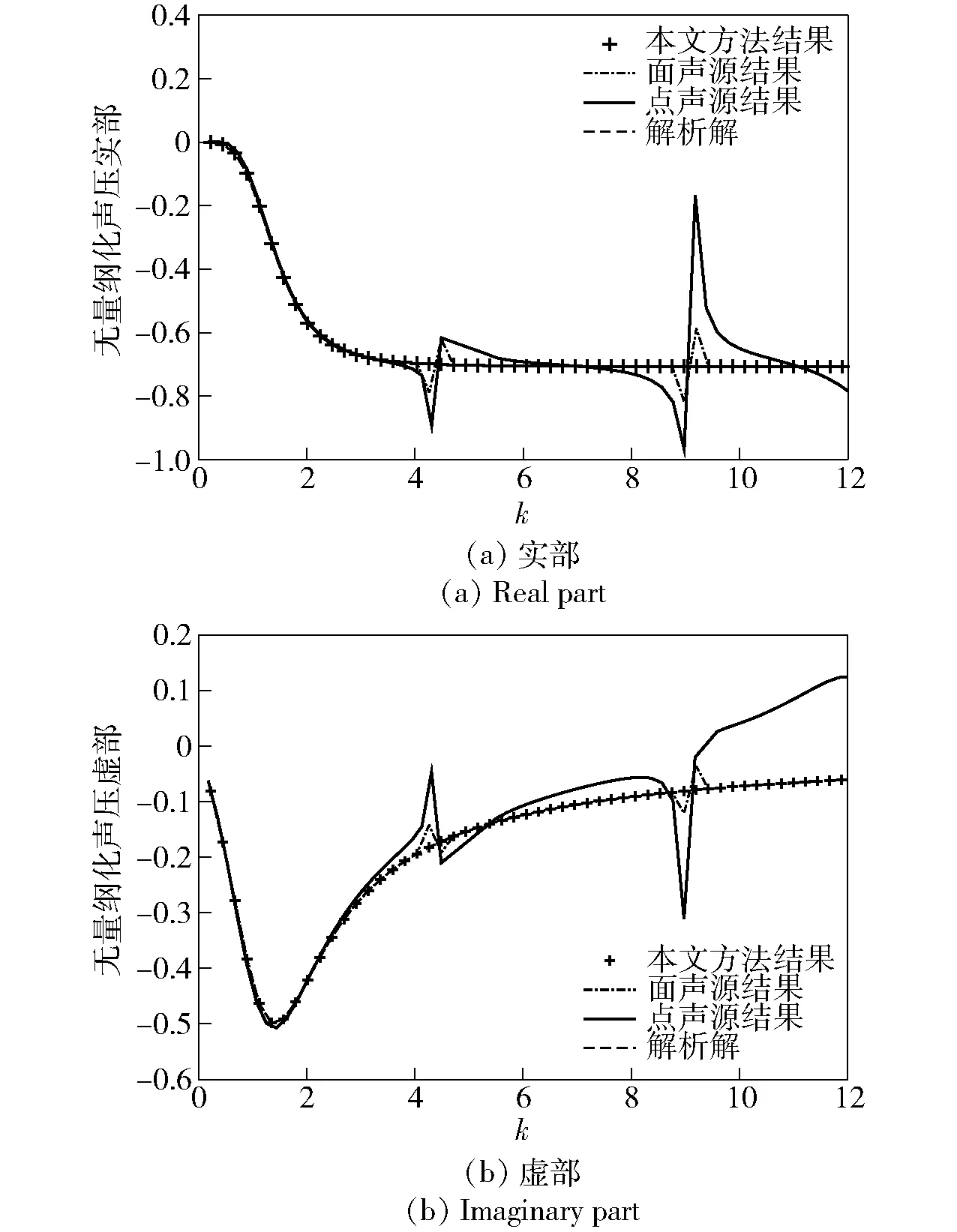
图9 横向振动球源φ=135°处无量纲化声压比较图Fig.9 Comparison of dimensionless sound pressures at laterally oscillating spherical source for φ=135°
从图7~图9可知,本文方法和面声源法的计算精度要高于点声源发的结果,点声源计算的误差随着频率的升高逐渐增大较多。当频率接近特征频率时,采用虚拟面声源法和点源法的结果偏离解析解较大,不能保证特征频率处解的唯一性。而采用面声源和点声源相结合的虚拟声源法所得结果在全频域内与解析解吻合得很好,不会在特征频率处发生偏差。
在横向振动球源的计算效率上,采用本文方法、虚拟面声源法和虚拟点声源法的单频计算时间分别为170.4 s、170.5 s和1.5 s,从中可以看出,点声源法的计算效率要远高于采用面声源计算声辐射参数的方法,这是由于采用面声源运算需要进行矩阵组装和积分运算,因而消耗了大量时间。
7 结论
根据波叠加原理,利用面声源和点声源作为非共面的虚拟声源,搜索与边界条件相匹配的真实声压与结构表面振速,本文提出了一种保证全频域解唯一的虚拟声源计算方法。该方法在结构内部同时布置虚拟面声源和点声源离散声场:面声源位于结构内部一个与结构边界共形的表面,用其匹配结构表面的声压与振速;点声源则位于虚拟表面内部,由于与虚拟表面不共面,因而可以保证解在特征频率处的唯一性。案例分析结果表明:
1)采用面声源匹配结构表面振速的精度要优于点声源的结果;在频率较高时,采用虚拟点声源计算的误差过大,因而虚拟点声源法不适合处理高频情形;为保证精度,可以采用虚拟面声源法处理高频情形,但相对于虚拟点声源法运算量成倍增加,这是由于采用面声源计算时需要进行积分运算,因此采用点声源的计算精度差但效率高。
2)与BEM相比,面声源和点声源相结合的虚拟声源法中,由于虚拟源位于结构内部,因此不需要处理奇异性问题,简化了计算过程,提高了计算效率;相对于单独采用点声源、面声源作为虚拟声源方法,联合虚拟声源方法可以保证解在全波数范围内的唯一性,且采用较少的单元就可以获得很好的计算精度。
参考文献(References)
[1] SUN F X, LIU C, CHEN Y M. An improved interpolating element-free Galerkin method based on nonsingular weight functions[J]. Mathematical Problems in Engineering, 2014(8):249-269.
[2] 夏百战,于德介,姚凌云. 二维多流体域耦合声场的光滑有限元解法[J]. 声学学报,2012,37(6):601-609.
XIA B Z,YU D J,YAO L Y. A smoothed finite element method for two-dimensional coupling acoustic fields in multi-fluid domain[J]. Chinese Journal of Acoustics,2012,37(6):601-609. (in Chinese)
[3] LIU J Y, RUDOLPHI T J. New identities for fundamental solutions and their applications to non-singular boundary element formulations[J]. Computational Mechanics,1999,24(4):286-292.
[4] ATALLA N,BEMHARD R J.Review of numerical solutions for low-frequency structural-acoustic problems[J].Applied Acoustics,1994,43(3):271-294.
[5] COYETTE J P,FYFE K R.An improved formulation for acoustic eigenmode extraction from boundary element methods[J].Journal of Vibration and Acoustics,1990,112(3):392-397.
[6] BURTON A J,MILLER G F.The application of integral equation methods to the numerical solution of some exterior boundary-value problems[J].Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences ,1971,323(1553):201-210.
[7] KOOPMANN G H,SONG L,FAHNLINE J B.A method for computing acoustic fields based on the principle of wave superposition[J].Journal of the Acoustical Society of America,1989,86 (6):2433-2438.
[8] SONG L,KOOPMANN G H,FAHNLINEJ B.Numerical errors associated with the method of superposition for computing acoustic fields[J].Journal of the Acoustical Society of America,1991,89(6):2625-2633.
[9] KOOPMANN G H,BELEGUNDU A D.Tuning a wine glass via material tailoring an application of a method for optimal acoustic design[J].Journal of Sound and Vibration,2001,239 (4):665-678.
[10] KOOPMANN G H,FAHNLINE J B.Designing quiet structures: a sound power minimization approach [M].San Diego, CA ,US: Academic Press, 1997.
[11] BENTHIEN G W,SCHENCK H A.Nonexistence and nonuniqueness problems associated with integral equation methods in acoustic[J].Computers & Structures,1997,65(3):295-305.
[12] JEANS R A,MATHEWS I C.The wave superposition method as a robust technique for computing acoustic fields[J].Journal of the Acoustical Society of America,1992,92(2):1156-1166.
[13] WILTON D T,MATHEWS I C,JEANS R A.A clarification of nonexistence problems with superposition method[J].Journal of the Acoustical Society of America,1993,94(3):1676-1680.
[14] XIANG Y,LU J,HUANG Y Y.A fast wave superposition spectral method with complex radius vector combined with two-dimensional fast Fourier transform algorithm for acoustic radiation of axisymmetric bodies[J].Journal of Sound & Vibration,2012,331(6):1441-1454.
[15] 向宇,黄玉盈,马小强.求解二维结构—声耦合问题的一种直接方法[J].振动与冲击,2003,22(4):40-44,31.
XIANG Y,HUANG Y Y,MA X Q.Direct solution to 2-D sound-structure interaction problems[J].Journal of Vibration and Shock,2003,22(4):40-44,31.(in Chinese)
[16] 夏雪宝,向阳,王校青,等.基于波叠加法的声辐射阻计算研究[J].船舶力学,2015,19(1/2):206-214.
XIA X B,XIANG Y,WANG X Q,et al.Research on the acoustic radiation resistance calculation based on wave superposition[J].Journal of Ship Mechanics,2015,19(1/2):206-214.(in Chinese)
[17] 夏雪宝,向阳.基于附加源波叠加法的声辐射计算研究[J].振动与冲击,2015,34(1):104-109.
XIA X B,XIANG Y.Acoustic radiation calculation based on additional sources wave superposition method[J].Journal of Vibration and Shock,2015,34(1):104-109.(in Chinese)
[18] 向宇, 黄玉盈. 伸缩虚拟边界元法解二维Helmholtz外问题[J]. 力学学报,2003,35(3):272-279.
XIANG Y,HUANG Y Y.The expanding-contracting virtual boundary element method for 2D-Helmholtz exterior problems[J].Acta Mechanica Sinica,2003,35(3):272-279.(in Chinese)
[19] GOLUB G H,VAN LOAN C F.Matrix computations[M].Baltimore, MD, US: Johns Hopkins University Press,1983:11-29.
[20] BORGIOTTI G V,SARKISSIAN A,Williams E G,et al.Conformal generalized near-field acoustic holography for axisymmetric geometries[J].Journal of the Acoustical Society of America,1990,88(1):199-209.
[21] ZELLERS B C. An acoustic superposition method for computing structural radiation in spatially digitized domains[D].State College, PA, US:The Pennsylvania State University,2006.
[22] HWANG J Y,CHANG S C. A retracted boundary integral equation for exterior acoustic problem with unique solution for all wave numbers[J]. Journal of the Acoustical Society of America,1991,90(2):167-180.
[23] GOUNOTY J R,MUSAFIR R E. Genetic algorithms: a global search tool to find optimal equivalent source sets[J]. Journal of Sound & Vibration,2009,322(1/2):282-298.
[24] PAVIC G. A technique for the computation of sound radiation by vibrating bodies using multipole substitute sources[J]. Acta Acustica United with Acustica,2009,92(1):112-126.
[25] 陈鸿洋,商德江,李琪,等. 声场匹配波叠加法的水下结构声辐射预报[J]. 声学学报,2013,38(2):137-146.
CHEN H Y,SHANG D J,LI Q,et al.Sound radiation prediction for underwater structure by field-matching wave superposition method[J]. Chinese Journal of Acoustics,2013,38(2):137-146. (in Chinese)
[26] WU S W,XIANG Y.Location optimization of monopole equivalent sources in wave superposition method[J].International Journal of Acoustics and Vibration,2018,23(2):254-263.
[27] 商德江,钱治文,何元安,等.基于联合波叠加法的浅海信道下圆柱壳声辐射研究[J].物理学报,2018,67(8):125-138.
SHANG D J,QIAN Z W,HE Y A,et al.Sound radiation of cylinder in shallow water investigated by combined wave superposition method[J].Acta Physica Sinica,2018,67(8):125-138.(in Chinese)
