基于SEIR模型的新冠肺炎疫情系统动力学仿真分析

周美含 葛洪磊 蒋薇 江通 高飞龙 吴静

摘 要：当前全球新冠肺炎疫情形势仍然非常严峻，对疫情进行仿真分析有利于加强疫情防控。文章考虑社区管制、交通管制、防护用具紧缺等因素，将感染者分为轻症感染者、重症感染者两类，移出者分为死亡者、痊愈者两类，对传统的SEIR传染病模型进行修正，建立了一个新冠肺炎疫情的系统动力学模型，对湖北省武汉市新冠肺炎疫情的演化和防控进行了仿真分析，并提出了相关建议。

关键词：新冠肺炎疫情;系统动力学;SEIR模型

中图分类号：O313 文献标识码：A 文章编号：1005-6432（2022）03-0005-03

DOI：10.13939/j.cnki.zgsc.2022.03.005

1 引言

2019年年底新冠肺炎疫情首先在中国、韩国、意大利、伊朗、西班牙、美国等国家暴发，随后短时间内席卷全球。根据国家卫生健康委员会以及WHO公布的数据，截至2020年4月23日，中国累计报告新冠肺炎确诊病例82804例，累计死亡病例4632例;全球累计报告新冠肺炎确诊病例超过270万例，累计死亡病例超过19万例。疫情暴发一年后，截至2021年3月20日全球累计报告新冠肺炎确诊病例已超过1.2亿，使全球遭受了巨大的生命威胁和经济损失。可见，当前全球疫情仍然非常严重，对新冠肺炎疫情进行仿真分析并提出防控建议具有重要意义。

自新冠肺炎疫情暴发以来，国内外专家纷纷开展了对疫情演化的研究。王建伟等（2020）以美国和中国新冠肺炎公开数据为样本，应用广义SEIR模型，对疾病传播参数进行估计，利用系统动力学模型进行参数敏感性分析，根据分析结果提出针对性的防控干预措施。杨守德和陈伟（2020）建立基于新冠肺炎传染特征的系统动力学仿真模型，结合不同的经济社会环境，对“经济运行优先型”“民众健康优先型”“兼顾平衡型”三种公共应对方案的防控效果及经济抑制影响进行综合考量。刘红亮等（2020）构建了基于系统动力学的新冠肺炎患者变动分析模型，对甘肃省确诊患者数量变动进行合理估计和预判。金新叶等（2020）发现交通管制在控制传染源、切断传播途径方面发挥了重大作用。王雁等（2020）在新冠肺炎疫情初期传播系统动力学模型分析结果的基础上，建立了意大利疫情传播综合预测模型。陈兴志等（2021）建立了一个SEIR流行病模型进行理论分析和数值模拟，根据结果对之前采取的一些控制策略做了分析评估，同时对疫情后期发展进行预测。Ben K N等（2021）通过建立多阶段SEIR模型来预测国际航班恢复后新疫情大流行的潜力。Yarsky P（2021）通过SEIR模型来预测新冠肺炎疫情在美国的扩散情况，并分析了对重新开放和医院资源利用情况的影响。

武汉曾经是我国的疫情重灾区，其疫情防控的成功经验对于我国其他地区以及其他国家疫情防控具有重要的参考价值。自武汉封城后，市内又实施了交通管制、社区管制、追踪并隔离染病者和密切接触者等一系列措施，使得武汉市内人与人接触率不断降低，病毒传播率也随之降低。除此之外，其他省市向武汉捐赠医疗设备并且派遣医疗团队进行支援，使得武汉市内的治愈率不断提高、死亡率不断降低。尽管目前已有一些研究基于SEIR模型对新冠肺炎疫情演化进行了仿真分析，但是以武汉市为研究对象的仍然不多。为了重新展现武汉抗击新冠肺炎疫情的成功经验，文章基于SEIR建立一个系统动力学模型来动态模拟武汉市新冠肺炎疫情的发展与防控情况，分析其成功的防控经验。

2 模型构建

2.1 模型假设

①武汉市总人口为常数，在模拟期内迁入人口、迁出人口、出生人口和非新冠肺炎死亡人口对总人口的影响忽略不计。②新冠肺炎痊愈者具备抗体，不会发生二次感染。③已经检测出的新冠肺炎轻症、重症感染者均被安全隔离，不再具有传染性。④感染概率受社区管制、交通管制、防护用具紧缺情况的影响，社区管制与交通管制程度越高，防护用具紧缺程度越低，感染概率就越小。

2.2 系统流图

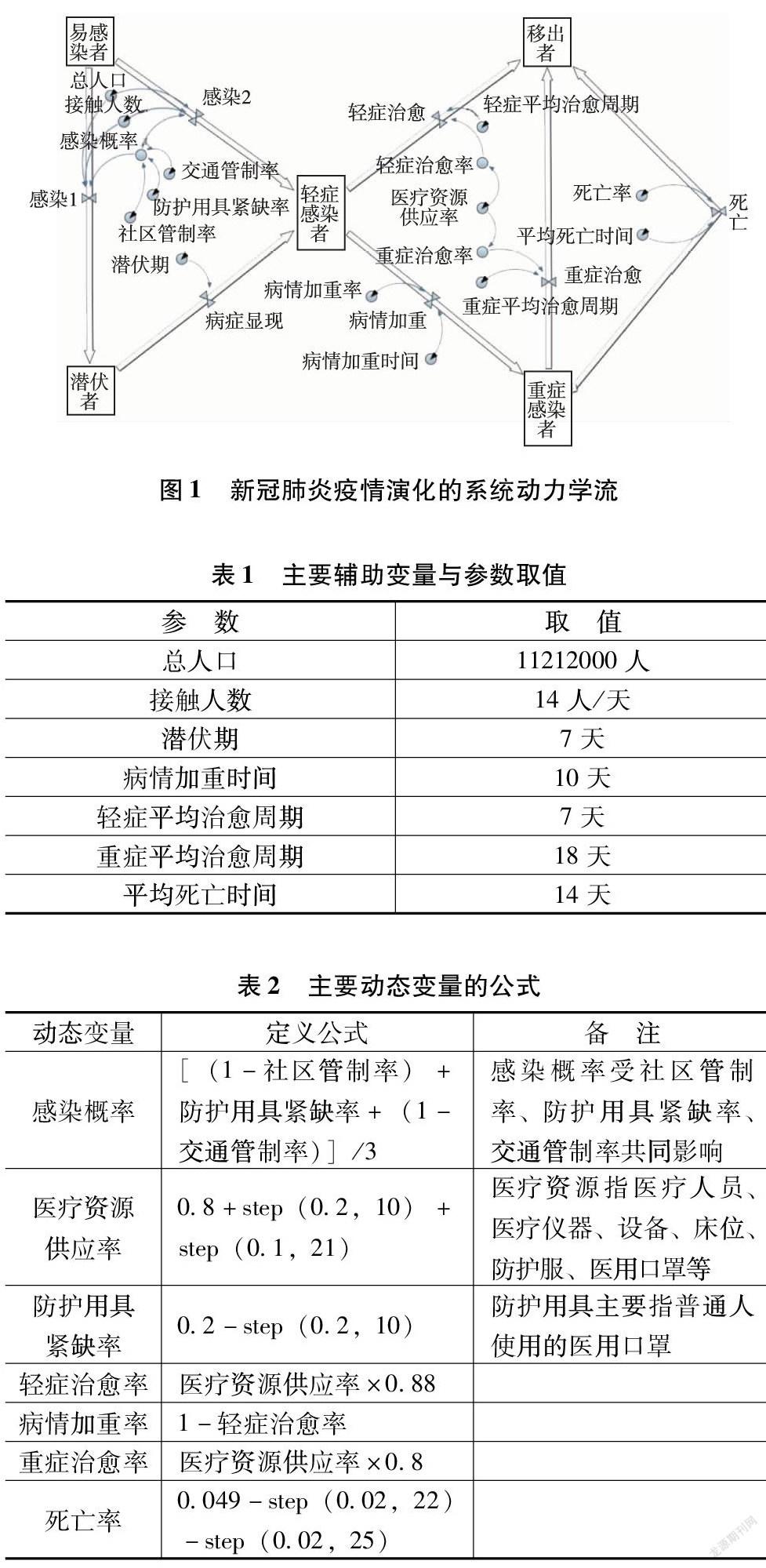
根据上述假设，对经典的SEIR模型进行修正，将人群分为四大类：易感染者（S）、潜伏者（E）、感染者（I）和移出者（R），其中感染者分为轻症感染者、重症感染者两类，移出者分为死亡者、痊愈者两类。基于SEIR模型，使用Anylogic软件得到新冠肺炎疫情演化的系统动力学流图，如图1所示。

2.3 辅助变量与参数设置

模型主要辅助变量与参数的设置均参考政府统计年鉴、政府部门发布会发布的数据，或参考“有来医生”“杏林健康”“香芒健康”等专业医学网站中的统计数据，具体如表1所示。

模型中主要动态变量的定义公式如表2所示。

3 模拟仿真

3.1 校准实验

由于社区管制率和交通管制率这两个参数缺乏有效的统计数据，因此通过校准实验来获得其取值。以2020年1月30日至2月29日武汉市轻症感染者人数和重症感染者人数的历史数据作为校准标准，权重均为0.5，目标是使得仿真数据与历史统计数据的差异最小。将社区管制率和交通管制率的参数类型设置为“连续”，取值范围为[0，1];当取值为0时表示没有任何管制，当取值为1时表示采取最严格的管制。设置迭代次数为500次。

经过多次校准，得到交通管制率：0.889，社区管制率：0.911，此时仿真数据与历史数据的差異最小，差异为2186.406。这两个参数的取值与现实情况比较相符，表示武汉实行了严格的交通管制和社区管制。此时，武汉轻症感染者、重症感染者历史数据与仿真数据的对比分别如图2和图3所示。可见，历史数据与仿真数据基本吻合，轻症感染者的吻合度更高一些。经过校准实验，模型的合理性得到验证。

3.2 参数分析

新冠肺炎疫情中的感染概率取决于疫情防控中的三个重要参数：社区管制率、交通管制率以及防护用具紧缺率。通过对这三个参数进行参数分析，可以了解这些疫情防控的关键因素对疫情演化的影响。

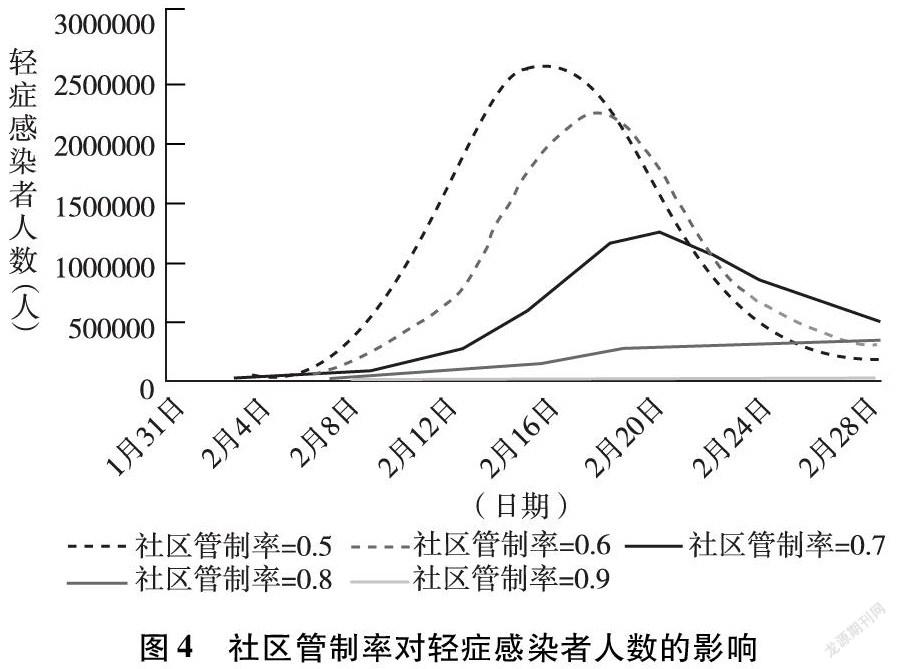
（1）社区管制率的参数分析。将社区管制率设为范围参数，最小值设为0.5，表示武汉市内半数社区采取管制措施;最大值设为0.9，表示武汉市内绝大部分社区均采取管制措施。步长为0.1，模拟时间30天。社区管制率对于轻症感染者人数的影响如图4所示。可见，当社区管制率减小，即放松社区管制时，轻症感染人数会明显增加。当社区管制率分别为0.8、0.7、0.6、0.5时，新冠肺炎轻症感染人数最高分别可达341420、1247000、2289000、2667000人，分别是现实感染人数的12、44、80、94倍。因此，新冠肺炎轻症感染人数对于社区管制率这一参数非常敏感。

（2）交通管制率的参数分析。将交通管制率设为范围参数，最小值设为0.5，表示武汉市内半数交通要道或交通工具采取管制措施;最大值设为0.9，表示武汉市内绝大部分交通要道或交通工具均采取管制措施。步长为0.1，模拟时间30天。交通管制率对于轻症感染者人数的影响如图5所示。可见，当交通管制率减小，即放松交通管制时，轻症感染人数会明显增加。当交通管制率分别为0.8、0.7、0.6、0.5时，新冠肺炎轻症感染人数最高分别可达226698、993593、2126000、2604000人，分别是现实感染人数的8、35、75、92倍。因此，新冠肺炎轻症感染人数对于交通管制率这一参数非常敏感。

（3）防护用具紧缺率的参数分析。將防护用具紧缺率设为范围参数，最小值设为0，表示武汉市内所有防护用具均能满足需求;最大值设为0.5，表示武汉市内防护用具满足需求率为50%。步长为0.1，模拟时间30天。防护用具紧缺率对于轻症感染者人数的影响如图6所示。可见，当防护用具紧缺率减小，轻、重症感染人数会明显减小。当防护用具紧缺率分别为0.5、0.4、0.3、0.2时，新冠肺炎轻症感染人数最高分别可达2836000、2392000、1287000、525548人，分别是现实感染人数的94、79、42、17倍。因此，新冠肺炎轻症感染人数对于防护用具紧缺率这一参数非常敏感。新冠肺炎现有确诊人数为轻症感染者人数与重症感染者人数之和。社区管制率、交通管制率以及防护用具紧缺率会对新冠肺炎现有确诊人数产生显著影响。

4 结论

文章基于SEIR模型建立了一个新冠肺炎疫情的系统动力学仿真模型，与历史数据相比较，仿真结果比较合理。通过参数分析发现，社区管制、交通管制和防护用具供应三个因素均会对疫情管控效果产生极大影响。社区管制与交通管制覆盖面越广，管制措施越严格，防护用具数量越充足，疫情防控效果就越好。因此，在新冠肺炎疫情发生之前应加大医用口罩等防护用具的生产储备和应急储备;在疫情扩散或疫情严重期间，地方政府应严格实行交通管制和社区管制，并加大防护用具的市场供应量和储备调拨量。2021年1月初，河北石家庄疫情的成功防控也进一步说明了这一点。

参考文献：

[1]BEN K N， KOLSI L， ALSAIF H. A multi-stage SEIR model to predict the potential of a new COVID-19 wave in KSA after lifting all travel restrictions[J].Alexandria Engineering Journal， 2021，60（4）：3965-3974.

[2] YARSKY P . Using a genetic algorithm to fit parameters of a COVID-19 SEIR model for US states[J].Mathematics and Computers in Simulation， 2021，185（3）：687-695.

[3]陈兴志，田宝单，王代文，等.基于SEIR模型的COVID-19疫情防控效果评估和预测[J].应用数学和力学，2021，42（2）：199-211.

[4]刘红亮，贾洪文，王雁，等.新型冠状病毒肺炎初期传播规模的系统动力学模型估计方法及评价——以甘肃省为例的研究[J].电子科技大学学报（社科版），2020，22（3）：36-45.

[5]王建伟，崔秩玮，潘潇雄，等.基于广义SEIR模型的新冠肺炎传播机制及干预效果仿真[J].科技导报，2020，38（22）：130-138.

[6]金新叶，卢珍珍，丁中兴，等.武汉交通管制和集中隔离对新型冠状病毒肺炎疫情影响的动力学模型研究[J].山东大学学报（医学版），2020，58（10）：25-31.

[7]王雁，吴继煜，刘红亮，等.新冠肺炎传播中期规模增长规律的模型建构与解析——基于意大利疫情数据的研究[J].西北人口，2020，41（4）：114-126.

[8]杨守德，陈伟.突发流行病短期公共应对方案防控效果及经济抑制影响研究——一个基于新冠肺炎传染特征的系统动力学仿真分析[J].软科学，2020，34（11）：130-136.

[基金项目]国家级大学生创新创业训练计划项目（项目编号：202013022021）;宁波市自然科学基金资助项目（项目编号：2019A610034）;浙大宁波理工学院商学院SRTP项目。

[作者简介]周美含，女，就读于浙大宁波理工学院，研究方向：物流与供应链管理;通讯作者：葛洪磊（1979—），男，浙大宁波理工学院副教授，博士，研究方向：物流与供应链管理。