模拟器基于开普勒参数的GLONASS 卫星位置预测∗

徐 倩 宋茂忠

（南京航空航天大学电子信息工程学院 南京 211106）

1 引言

GLONASS 实时模拟器普遍使用的是DSP+FPGA 架构，以DSP 为控制核心进行复杂的数字运算［1~2］。DSP 端需要实时将计算的卫星号、载波频率字、码频率字、码初相和电文初相等数据传送给FPGA 处理［3］。GLONASS ICD 建议采用四阶Run⁃ge-Kutta数值积分法来计算卫星位置［7~8］，该算法需反复迭代，积分步骤太多，难以满足GLONASS模拟器的实时计算［4］。

针对GLONASS 积分运算的弊端，柯福阳等提出了自动积分步长的龙格库塔积分法，在原有积分模型基础上进行优化，但是效果有限［5］，朱海波等提出了一种快速定轨方法，每一历元只需由上一历元信息通过一次积分即可算出，但是历元之间的数据具有依赖性［6］。积分法如果想在一段较长的时间内保持计算精度，必然意味着反复迭代。

而开普勒轨道根数法计算卫星位置，公式简单，无需反复迭代［9~10］，本文提出了一种基于开普勒轨道根数的GLONASS 卫星定位算法，通过导航电文先获得多组卫星的位置矢量数据，然后通过拟合算法将GLONASS卫星位置的计算通过一组轨道参数来实现。所有位置的计算只依赖于一组星历参数，满足了模拟器实时传输数据的需要。

2 轨道根数拟合算法

轨道根数可以用于描述卫星在太空中运行位置、运动方向等状态信息。对轨道根数的求解精确程度也大大影响着我们定位算法的精确度。轨道根数的拟合大多数利用的是卫星在运行轨道中的位置坐标，拟合出的结果表示为六个开普勒轨道根数和九个摄动调和参数［11］。

2.1 基本模型

由于GPS是目前最为成熟的卫星系统，我们以GPS的6个开普勒轨道参数和9个摄动参数作为状态参数进行拟合。由多个离散的卫星地固坐标位置，可以拟合出相应的状态参数。这里离散的坐标位置我们通过GLONASS 的导航电文，由Run⁃ge-Kutta积分算出。

根据GPS卫星位置的计算方法，我们列出算法的状态方程和观测方程为

式中Y是观测列矢量，含m个观测量，每个列矢量都对应相应时刻的卫星位置分量。t是位置坐标对应的时刻，t0是状态参数的参考时刻，X表示卫星的状态参数，X0即是待估测的状态参数，这里取

由于式（1）和式（2）都不是线性方程，无法直接求解。于是为了求解，我们必须将这两个方程线性化，并进行迭代求解。

令Xi0是状态参数X0的第i次迭代的初值，由此可以将式（2）在Xi0处进行展开，舍去二阶以上的小量，得

令

x0表示状态参数第i次迭代的初值Xi0所求的值X0的差：

y表示t时刻下的观测列矢量与第i次迭代的初值Xi0所求的观测列矢量的差：

于是，

式中：v为误差方程。

根据最小二乘原理，可得

因此，每次迭代后，状态参数为

当满足式（12）时，不再迭代。

2.2 卫星位置矢量对状态参数的偏导数

经过转换可得

由式（13）和式（14）可推出观测列矢量对所求状态矢量的偏导数，这里不再给出推导过程。

将所得偏导数计算结果带入式（7），经式（10）反复迭代后，即可求得满足精度需求的6 个开普勒轨道根数和9 个摄动参数，再将该参数用于GLONASS 模拟器计算卫星位置，即可实现在满足卫星位置精度需求的同时，极大地降低了求解的时间复杂度。

3 GLONASS卫星数据验证

选用GLONASS 导航系统7 号卫星的数据进行测试，第一个历元选取2017 年5 月12 日10 时15分，拟合算法共选取了8 个历元，历元间隔3 分钟，第一个历元为2017 年5 月12 日10 时15 分，最后一个历元间隔为2017 年5 月12 日10 时36 分。由于导航电文只能提供15分、45分时刻的导航数据，因此其他时刻的卫星位置数据只能通过其最近时刻的已知卫星位置数据用Runge-Kutta积分法算出。

图1是由8 个卫星位置拟合出的6 个开普勒轨道参数和9 个摄动参数结果。对应的时间是GPS周1948，GPS周内秒339300.000。

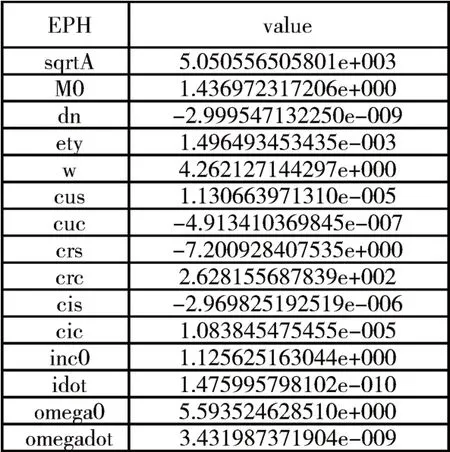
图1 3分钟间隔拟合开普勒参数

图2是两种方法计算出的八个点的卫星位置误差图，不同坐标分量由不同颜色表示。

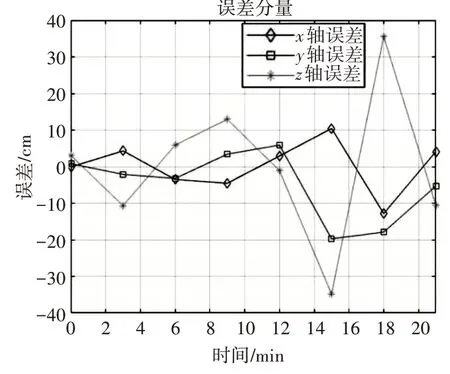
图2 不同坐标分量的误差图

由图2 可知，随着时间的后移，外推能力逐渐减弱，误差开始增大。在图3 所示的时间内，卫星位置外推算法的精确性都可以得到保证，各个坐标分量的误差不超过40cm，GLONASS 导航电文每隔30min 更新一次，最大外推时间为前后15min，该拟合算法完全可以满足GLONASS卫星导航系统的精度需求。

上述数据是由原始数据每3min 一个卫星位置拟合得出，为了获得更加精确的拟合结果，我们还可以改变卫星位置的间隔时间，研究不同间隔时间下的卫星位置拟合出的开普勒参数所计算出的卫星位置的精确性。

图3~5是GLONASS 5 号 卫 星 在2020 年2 月21日2 时15 开始的以2min 间隔、3min 间隔、4min 间隔、8min 间隔、12min 间隔下的拟合结果计算出的卫星位置不同分量下的对比误差图。

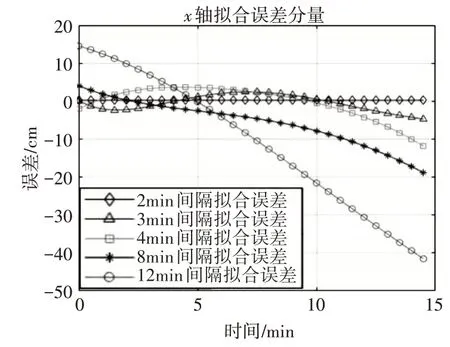
图3 不同间隔下的X轴的误差图

图4 不同间隔下的Y轴的误差图

图5 不同间隔下的Z轴的误差图

由图可知，用于拟合的卫星位置间隔越小，拟合出的开普勒参数精度相对越高，计算出的卫星位置越精确；所有间隔的拟合精度都呈现出了随着外推时间的推移，精度越来越低的现象，在GLONASS卫星前后外推15min 的时间内，小间隔拟合能够保持一个较高的精度，满足了实时卫星导航模拟器的计算需求。

4 结语

本文设计的开普勒参数拟合算法能够生成较为精确的开普勒轨道根数，拟合外推时间远大于GLONASS 星历的最大外推时间，可在不改变GLONASS 广播电文参数的前提下，在客户端用于GLONASS 卫星导航系统卫星位置的计算。算法只需通过C++软件平台实现，成本低、效率高，能够更精确、更快地计算出卫星位置，避免了Runge-Kutta积分的反复迭代，具有一定应用价值。