基于强化学习的装箱问题研究∗

纪乃华 李祥栋 祝 凯

（青岛理工大学信息与控制工程学院 青岛 266520）

1 引言

装箱问题（Packing Problem）是一种典型的组合优化问题，且已被证明是一个NP-hard 问题。装箱问题结合不同的约束条件和目标被广泛应用于制造业，运输业，计算机行业中。本文主要讨论二维带装箱问题2DSP（2D Strip Packing Problem），问题的定义为给定一组n个尺寸为wi×hi，i= 1…n的二维矩形物品；将这一组矩形物品不重叠，不旋转地放入到宽度为W，高度不限的矩形长板中，其目的是最小化其高度H。

针对装箱问题，学者们提出了大量基于不同策略的算法，大致可以分为三大类，第一类是精确算法，其中包括树搜索算法［1］，线性规划算法［2］等。第二类为近似算法，包括BL［3］、BF［4］等算法。第三类为启发式算法，包括元启发式算法中的遗传算法［5］，模拟退火算法［6］等，还有学者提出的混合式启发式算法包括Leung［7］提出的两阶段智能搜索算法，Yang［8］提出的简单随机算法都取得了不错的结果。

近年来伴随着人工智能的发展，作为人工智能的一种，强化学习可以直接在数据中提取有用的信息，从而可以潜在地学习更好的启发式算法，同时有着更好的通用性。强化学习广泛应用到组合优化问题上，例如旅行商问题（TSP）［9］，车辆路径问题（VRP）［10］。Bello［11］等提出了一种基于强化学习的神经组合优化框架，此框架在旅行商问题和背包问题上获得了不错的结果。针对组合优化问题的复杂性，强化学习的Q 函数和人工神经网络相结合的深度Q 网络（DQN）展现出了其强大的性能，KunDu［12］等提出了一种基于双DQN 的深度强化学习框架进行了在线二维装箱问题研究。虽然强化学习在解决组合优化问题上有着比启发式算法更好的性能，但强化学习的性能受到训练数据的影响，如何在使用小实例的样本训练后能够适用于较大的问题的实例成为强化学习解决组合优化问题的关键。

在Deep-Q-Network（DQN）和简单随机算法（SRA）的基础上，本文提出了一种混合启发式算法。本文的主要贡献如下：

1）提出改进了的评分规则Scorer I。装箱问题难免出现空间的浪费，按现有的评分规则进行装箱问题时浪费较多，本文通过引入了一组松弛因子（relaxation factor）α，β，建立更细致的评分规则，以最大程度减少空间浪费。

2）提出基于DQN 的评分规则Scorer II。本文通过强化学习的DQN 建立评价函数Scorer，再利用Scorer 对矩形物品评价得分得到降序排序的序列，将此序列作为启发式算法的初始序列，与其他简单排序（直接按照周长、宽度等）的初始化序列相比，提高了空间利用率。另一个优点是有效地避免了启发式算法陷入局部最优，有效减少算法的迭代次数。

3）算法融合。为克服模拟退火设置的参数较多、通用性较差的缺点，提出DQN 和SRA 相结合得到混合启发式算法（RSRA），其中评分规则为Scor⁃er I与Scorer II共同确定。

2 基于强化学习的启发式算法

2.1 skyline算法

skyline 算法是本文的启发式算法所使用的基本框架，skyline 算法用来确定矩形物品的排列规则。其算法步骤为对于一个给定的矩形序列，重复以下4 个步骤直到所有矩形都被填充：1）找到sky⁃line 中最低并且最左边（以最低为优先）的线段；2）根据评分规则从原始序列中依次计算适应度值；3）将适应度值最高的矩形物品放置在此处；4）更新skyline。

2.2 新的skyline评分规则

本文在高东琛［13］，Leung［7］等的评分规则基础上提出了新的评分规则Scorer I。其评分规则如下。

如图1 所示，选择skyline 中最低和最左边的线段，记在此线段上的放置空间为S（图中蓝色框内），候选线段为slowy，与slowy相邻的水平线段的高度差值较大的为h1，较小的为h2，slowy的宽度记为slowy.w，矩形物品的高和宽分别记为r.h，r.w。未放置的矩形物品序列中宽度最小的矩形物品记为rmin，其宽度记为rmin.w。空间S放置矩形物品后所剩余的空间记为A（图中虚线框内），其宽度为A.w（A.w=slowy-r.w）。

图1 矩形物品放置空间示例

高东琛提出的评分规则的不足之处在于：

1）高东琛在Leung［7］基础上引入“松弛因子”并建立了更详细的规则，该规则考虑了矩形物品高度过大时将适应度值设为较低值，选取高度较低的矩形物品放在slowy后，更新skyline，然而该规则在公开数据集实际试验效果并不理想，由于新的slowy位置有可能变为更高的位置，较高的矩形物品放置在此处，有可能会导致整体高度增加。鉴于此种情况，本文不将矩形物品的高度作为评分的标准，能够有效避免整体高度过高。

2）高东琛考虑到很多时候不存在恰好相等的情况，适当的空间浪费是有必要的，通过松弛因子进行比例的控制，优先选择浪费较少的是一个合理的策略，但是根据此松弛因子在实际实验中并不能确定放入物品后所剩余的空间能否再放入未放置物品中最小的矩形，针对此种情况本文提出在每一次放置物品时，将所剩余空间的宽度与最小的矩形的宽度进行比较。

综上，关键在于最大利用每一个空间，之前都是考虑单步one-step 放置，本文通过对two-step 两步放置矩形的综合考虑，并引入一组宽度松弛因子，主要改进如下：

1）本文提出了记录待放入矩形物品中的最小矩形物品（rmin）的宽度（rmin.w），在装箱过程中不可避免有浪费空间的情况存在，在此时考虑如果将矩形物品放入之后的宽度是否能够满足大于rmin.w，如果大于，则表明在此空间能够继续放入矩形物品，不会造成浪费，否则会造成空间的浪费。

2）当造成空间浪费的情况时，加入了一组松弛因子（α，β，0<α<1，0<β<1），此系数能够在必须造成空间浪费的情况下，考虑到最小剩余空间思想，选取宽度较大的矩形放置，能够最大程度减少空间浪费，根据试验，本文取值α=0.2，β=0.5。

3）本文还对一些细节进行了优化，本文认为当r.w=slowy.w且r.h=h1或r.h=h2，因为能够减少sky⁃line 的线段数，并能够使得空间更加的平整，所以此处更加适合放置。同时r.h=h2时，相比于r.h=h1时更能够使得空间更加的平整，更有利于接下来的矩形物品放置，所以本文认为前者得分更高。本文还进行了一些细节的改变。

其详细的适应度值如图2（a）~（f）和表1所示。

表1 适应度值（fitness）表

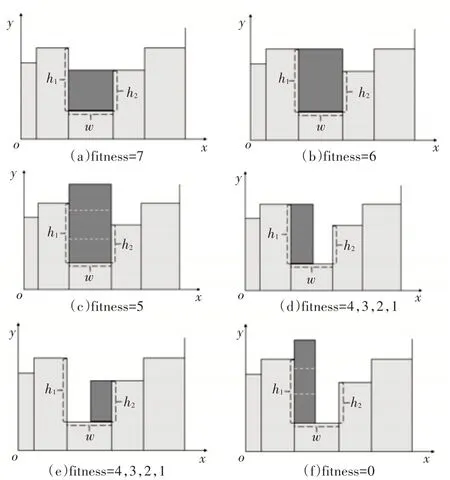
图2 适应度值示例

2.3 强化学习方法

与监督学习不同的是强化学习从没有可用的数据开始，这些数据是算法在整个过程中动态收集的。强化学习最常用于需要顺序决策的应用中，其目的是做出最大化回报的决策。

2.3.1 DQN

Q-learning算法是强化学习中的基于价值（val⁃ue based）的算法中的一种，Q（s，a）是表示在状态s的情况下执行动作a的奖励值，Q函数选择奖励值最大的动作执行。Q-learning算法中的Q是一个表格函数，显然是不适用于2DSP的，于是我们采用将Q-learning 与神经网络相结合的Deep Q-Network（DQN）。DQN 算法的核心是用一个人工神经网络来代替Q（s，a），神经网络有着强大的表达能力，能够自动寻找特征，神经网络要比人工寻找特征强大许多。

2.3.2 DQN神经网络以及数据预处理方法

本文使用的人工神经网络结构如图3所示。

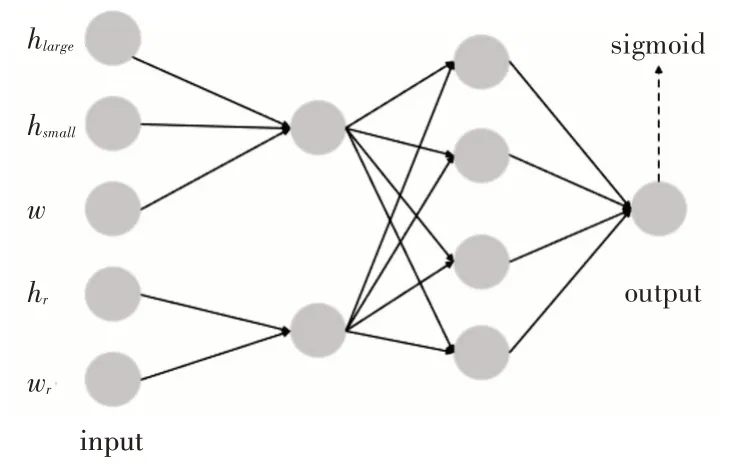
图3 人工神经网络score

数据预处理过程如表2 所示，其输入数据hlarge表示待放入矩形物品的高度r.h与h1的高度差，hsmall表示r.h与h2的高度差，w表示r.w与待放入空间的宽度slowy.w的差值，hr表示当前放入的矩形物品r与未放置的矩形物品序列中的高度最大矩形(R-r)hmax的相对高度，wr表示当前放入的矩形物品r与未放置的矩形物品序列中的宽度最大矩形rwmax的相对宽度。

表2 数据预处理过程

人工神经网络输出的数据只包含一个数，表示矩形物品r与待放入空间S的匹配度，值越大表示匹配度越高。hlarge，hsmall与w三个属性一起经过线性变换和激活函数tanh之后得到一个中间值。hr与wr两个属性一起经过线性变换和激活函数tanh之后得到一个中间值。在前两个已得到的中间值先经过一个2×4的线性变换和激活函数tanh，再经过4×1的线性变换和激活函数sigmoid得到最终的结果，其sigmoid的值域为（0，1）。

2.4 基于DQN的启发式算法（RSRA）

我们将使用前文提出的DQN 进行评价函数的构建，实验结果表明此算法与按照宽度，长度，周长的大小排列顺序所构建的矩形物品序列相比有着更好的性能。其详细算法如算法1 所示：在第二行中，使用了Leung［7］提出的局部搜索算法（LS（R）），以获得更好的解。LS（R）将在给定的序列中依次交换这两个项，并使用skyline算法以获得局部最优解。算法第7 行使用本文提出的skyline 算法评分规则Scorer I和Scorer II规则共同决定，即当使用规则Scorer I 得到的评分相等的情况下则采用Scorer II 规则。将DQN 和启发式算法相结合能够使用较少的数据样本进行训练，同时又能够应用到较大的问题实例上，具有较好的通用性。

算法1 基于强化学习的启发式算法

基于强化学习的启发式算法（RSRA）

Input：矩形物品序列R（r1，rn，…，rn）

Output：矩形长板高度

1：RßSort（Scorer II（R），descending order）

2：LS（R）

3：while 未超过规定程序运行时间do

4： fori←1 tondo

5： 在R中随机选取两个序列号j和k；

6： 在R中交换j和k的顺序获得新的序列R*；

7： currenth ←skyline（R*，α，Scorer）；

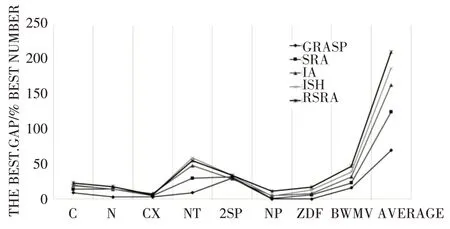
8： if current

9： besth ←currenth；

10： R ←R*；

11： else

12： p ←currenth/（currenth+besth）；

13： if p

14： R ←R*；

15： end if

16： end if

17： end for

18：end while

19：return besth；

3 实验分析

为了验证RSRA 的性能，我们将其与目前优秀的算法进行比较，其中包括GRASP［14］、SRA［8］、IA［15］和ISH［16］这三个算法。

我 们 所 使 用 计 算 机 为Intel（R）Core（R）i5-4210M CPU 2.60 GHz RAM 8GB，使用python 对RSRA 进行算法实现，其余算法结果来自原文文献，计算机配置分为Intel（R）Xeon（R）CPU E5405 2.00 GHz 1.99 GB RAM。

图4~7 为具体实验数据，Gap%的定义如Leung所示，Gap%=100×（mean-LB）/LB，其中mean 为算法运行10次所得到的平均结果。Ave.Gap%和best.Gap%分别表示算法运行10 次所得到的平均和最佳Gap%。

图4 和图5 显示了Ave.Gap%以及Best.Gap%五种算法的8个数据集。对于Ave.Gap%如图4所示，与其他四种算法相比，RSRA 算法在所有8 个数据集上都取得了最好的结果。对于Ave.Gap%，RSRA算法比GRASP 算法、SRA 算法、IA 算法和ISH 算法分别降低了45.86%、45.16%、30.89%和20.56%。对于Best.Gap%如图5 所示，RSRA 算法在8 个数据集中得到了6 个数据集（C、N、CX、NT、NP、BWMV 的数据集）的最小值。Best.Gap%的平均值RSRA 算法比GRASP 算法、SRA 算法、IA 算法和ISH 算法分别降低了48.86%、35.21%、18.76%和9.57%。

图5 Best.Gap%

图6 和图7 显示了Ave.Gap%以及Best.Gap%五种算法在所有数据集上所得到的最优解的数量。对于Ave.Gap%，RSRA 算法分别在6 个数据集（C、CX、NT、2sp、NP、BWMV）获得的的最优解数量最多，且最优解总数最多。对于Best.Gap%，RSRA 算法在5 个数据集（C，N，NP，ZDF，BWMV）上获得了最多的最优解数量，并且最优解数量的总和最大。

图6 Ave.Gap%五种算法获得最优解的数量

图7 Best.Gap%五种算法获得最优解的数量

根据数据集各自的特征进一步分析。如图4所示，虽然RSRA 的结果比其他四种算法好得多，但与GRASP 和ISH 的结果非常接近。这可能是因为2sp 的数据集太小（大多数实例都是n≤50）。对于CX 和ZDF 数据集（包含n≥10000 个实例），RSRA 的性能比其他四种算法要好得多。对于其他5个数据集（C、N、NT、NP、BWMV）中的问题实例数量大多为50 ≤N≤200，RSRA 算法也取得了不错的结果。因此，我们可以得出结论，RSRA 算法在8 个数据集上的性能优于其他4 个算法，尤其是在相对较大的数据集上。

图4 Ave.Gap%

4 结语

本文提出了一种求解2DSPP 问题的混合启发式算法，提出了改进的skyline 评分规则Scorer I，提出使用DQN 作为启发式算法评价函数Scorer II 的构建，Scorer I 和Scorer II 能够降低空间的浪费，降低启发式算法的迭代次数，提高算法的性能。提出Scorer I 和Scorer II 与一个SRA 算法相结合的混合启发式算法（RSRA）。实验结果表明，与其他四种优秀的启发式算法（GRASP、SRA、IA、ISH）相比，RSRA 在8 个数据集（C，N，CX，NT，2sp，NP，ZDF，BWMV）上取得了最好的性能，并且Ave.Gap%分别比GRASP、SRA、IA、ISH 分 别 降 低 了45.86%、45.16%、30.89%和20.56%。我们可以得出结论，RSRA 算法在8 个数据集上的性能优于其他4 个算法，尤其是在相对较大的数据集上。