非线性调频信号激励下非线性系统的最优共振响应*

2022-03-18宫涛杨建华单振王志乐刘后广

物理学报 2022年5期

宫涛杨建华单振王志乐刘后广

(中国矿业大学机电工程学院,江苏省矿山机电装备重点实验室,徐州 221116)

非线性调频(NLFM)信号在雷达、通信、信号处理中应用广泛,该类信号所激励下的非线性系统响应有着丰富的信息,通过共振来增强NLFM 信号具有一定实际意义与价值.本文主要研究了受到不同类型NLFM信号所激励的非线性系统共振现象,提出了实时尺度变换方法来处理高频NLFM 信号,克服人为选择造成信号输出响应较差的缺点.同时,提出实时谱放大因子作为共振评价指标,准确评价NLFM 信号激励下的系统共振响应,讨论系统参数对系统最优共振响应的影响,参数选择在合理的区间内即可实现最优共振响应,不仅实现信号特征的大幅增强,还保持信号时频特征的连续性.最后,将实时尺度变换方法和固定尺度变换方法进行对比,说明所提方法处理NLFM 信号的优越性.

1 引言

共振是系统响应中一种典型的动力学现象.通常来讲,对于简谐激励,当外激励频率接近于振动系统固有频率时会发生共振现象,此时系统振动振幅会急剧增强.不同于传统意义的共振,随机共振(stochastic resonance,SR)[1]、振动共振(vibrational resonance,VR)[2]得到广泛研究,利用其独特的动力学特性可以增强微弱的信号.其中随机共振是在微弱低频信号、噪声和非线性系统协同作用下使得系统输出得到显著增强的一种动力学现象,最初由意大利学者Benzi 提出[3],之后在信号处理中得到广泛应用[4-6].随机共振发生的基本条件是输入的微弱信号满足小参数条件,即信号频率远小于1.而实际中的信号大部分不满足小参数条件,为了实现大参数信号的随机共振,一些尺度变换方法被引入,比如二次采样[7]、频移尺度变换[8]、归一化尺度变换[9]、普通尺度变换[10].振动共振与随机共振类似,区别是输入的噪声被高频辅助信号代替,尺度变换方法与随机共振的方法一致.而单个信号激励下的系统共振[11]是指不需要辅助信号,依靠系统参数变化实现系统输出增强的一种现象,该现象有一定实际意义与价值,在信号增强方面,无需额外的高频辅助信号、噪声即可实现信号的增强,操作方便,实现过程简单.

在信号处理领域,利用共振现象来增强不同类型的信号具有独特的优势,相较于其他信号处理算法,如经验模态分解[12]、变分模态分解[13]、小波变换[14]、信号滤波[15]等方法,该类方法不仅可以增强信号,而且可以有效抑制干扰噪声.因此,基于共振的方法在信号处理中应用广泛.许多学者利用最优共振现象来增强和处理各类信号,比如简谐信号[16]、非周期二进制信号[17]、M-ary 信号[18]、频率调制(frequency modulation,FM)信号[19,20]等.其中FM 信号在雷达[21]、通信[22]、信号处理[23]中应用广泛,该类信号的特点是频率受到调制,按照其瞬时频率变化的规律主要分为线性调频(linear frequency modulation,LFM)信号和非线性调频(nonlinear frequency modulation,NLFM)信号,目前已有一些LFM 信号激励下的非线性系统动力学行为的研究,但是针对NLFM 信号的相关研究很少,考虑到NLFM 信号[24-26]广泛存在,如何实现NLFM 信号最优共振增强效果及NLFM 信号激励下的非线性系统最优共振响应的研究是一个有实际意义与价值的问题.

目前关于系统共振的研究,主要针对周期信号,其信号频率固定,通过尺度变换方法即可满足共振的小参数要求,调整合适的系统参数可实现最优共振响应.但是对于复杂NLFM 信号,其频率随时间非线性变化,此类信号的频率变化复杂,信号在频谱图中表现为连续频带,而且之前所用的尺度变换方法没有考虑频率的变化性,采用傅里叶变换方法无法准确描述信号特征,需要借助一些时频分析方法来描述.因此,针对NLFM 信号激励下的最优共振响应研究具有一定的难度与复杂性,采用的技术较周期信号的研究也更为复杂,采用固定尺度系数的尺度变换方法来处理NLFM 信号显然不能满足要求,无法实现最优参数匹配,系统输出响应效果较差.同时,NLFM 信号激励下的系统共振响应有一定的理论研究价值,对于实现NLFM 信号增强有一定的意义.基于此,本文研究了NLFM 信号激励下的非线性系统最优共振响应,提出了一种时变尺度系统共振方法有效实现复杂NLFM 信号的增强.该方法的基本原理是利用实时变化的尺度系数来匹配瞬时频率变化的NLFM 信号和系统参数,以尽量保证在每一时刻信号的瞬时频率满足最优小参数条件,通过调整系统参数和尺度系数实现最优共振响应.

本文提出了时变尺度系统共振理论,同时定义了新的共振评价指标-实时谱放大因子,可有效评价NLFM 信号的共振增强效果;处理了两类典型的NLFM 信号,研究了相关参数对最优共振响应的影响,在保证信号时频特征连续性的同时,实现了信号的共振增强,与固定尺度变换方法相比,本文所提方法克服了尺度系数选择人为性造成信号增强效果较差的缺点.

2 时变尺度系统共振理论

一种时变双稳态系统共振模型的动力学方程表示如下:

其中a(t),b(t)分别为时变系统参数 (a(t),b(t)≫1),系统为双稳态系统.x(t) 为系统的输出,s(t) 为输入的NLFM 信号.NLFM 信号s(t) 的瞬时频率f(t)随时间不断变化,为实现尺度系数与信号s(t)及系统参数a(t),b(t)相匹配,引入时变尺度系数β(t),表达式为

其中β0为尺度系数常数,f1(t)为s(t)的瞬时频率f(t)的离散化表示,β(t) 满足条件β(t)≫1.同时,系统参数a(t),b(t)与时变尺度系数β(t)满足以下关系:

其中a1≪1,b1≪1,(5)式满足系统共振小参数条件.(5)式相较(1)式,NLFM 信号s(t)幅值缩小到1/β(t),将(5)式的NLFM 信号幅值乘以β(t),变为

若系统共振发生在(6)式中,则系统共振也发生在(7)式中:

(7)式为一个大参数共振模型,可检测任意大频率的信号.

谱放大因子是经典的共振性能评价指标,针对NLFM 信号,信号的瞬时频率非线性变化,利用谱放大因子难以刻画NLFM 信号的共振效果.因此,本文定义了一种实时谱放大因子η来刻画NLFM信号激励下的系统共振效果,如下式:

其中η为系统输出的特征频带的放大程度,N为总数据点数,M为频率曲线f(t) 两侧的频带宽度m对应数据点数,X(·) 和S(·) 分别为输入信号和输出信号的离散短时傅里叶变换谱值,p(f(ti)) 为ti时刻信号的瞬时频率处点的位置.核心是在STFT 频谱上定义谱放大因子,将输出信号STFT 频谱图中信号时频一定范围内的能量之和与输入NLFM 信号的时频图中脊线能量之比作为评价指标,综合考虑NLFM 信号的时频特征,描述系统的共振响应更准确、可靠.若η＞ 1,说明NLFM 信号被有效增强.

3 几种不同NLFM 信号增强仿真分析

3.1 分段NLFM 信号

分段NLFM 信号较为典型,在机械设备信号处理中十分常见,由轴承、齿轮等零件经过复杂路径产生的信号为FM 信号,按照转速变化的特征,会产生反映零件运行状态的LFM 信号和NLFM信号.其中与分段NLFM 信号频率特征相对应的信号也很常见,比如文献[27,28]中这类转速工况,矿井提升机运行的典型转速工况为速度曲线线性上升-平稳-线性下降,反映出提升过程是线性加速-稳速-线性减速,这样的转速是人为控制的,关键部位的轴承故障特征信号均为此类分段NLFM 信号;流水线上的工业机器人的零件运行工况所产生的信号也为此类NLFM 信号,在故障诊断领域该类信号很常见,应用广泛,此类信号具有一定的代表意义.

一种典型的分段NLFM 信号s1(t)的频率f(t)随时间变化的分段函数为

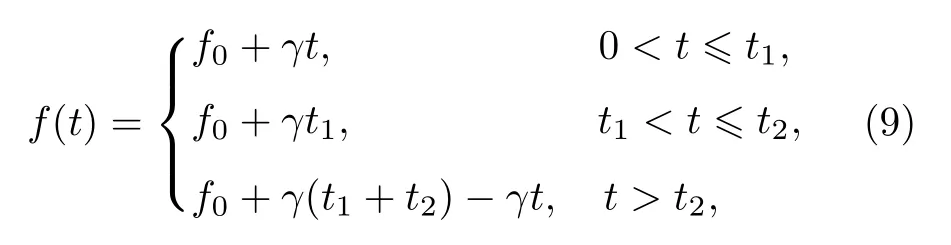
其中f0为起始频率,γ为频率变化率,t1,t2分别为频率规律发生变化的时刻.对应余弦函数的NLFM信号s1(t)描述为

其中A为信号幅值,φ为初始相位,s1(t)的频率变化规律为线性上升-不变-线性下降.

图1 给出了该NLFM 信号的相关信息,图1(a),(b)分别为信号的时域波形图和STFT 频谱图,在STFT 频谱图中可以观察到信号的频率特征曲线在0—3 s 内从0 Hz 增大到150 Hz,然后保持至7 s,最后降到0 Hz.

针对图1 中的信号,图2 分别给出了不同尺度系数下的系统输出实时谱放大因子η随系统参数a1的变化曲线,选取的固定尺度系数有β=β0×10,β0× 75,β0× 150,时变尺度系数有β=β0×f1(t),在固定尺度系数方法下的系统输出实时谱放大因子η随着尺度系数的增大而增强,在最大值处实现了NLFM 信号最优系统共振响应.同时,在时变尺度系数方法下的系统输出实时谱放大因子最大值ηmax比β=β0× 150 时的最大值略小,但是区别不大.

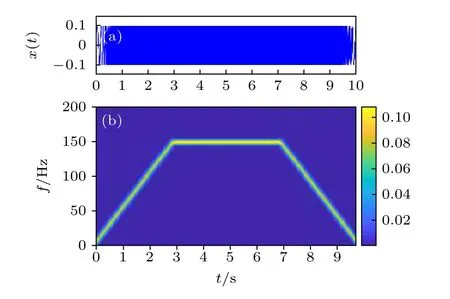
图1 输入的NLFM 信号 (a)时域波形图;(b) STFT 频谱图 (仿真参数A=0.1,f0=0,γ=50,φ=0,t1=3,t2=10)Fig.1.The input NLFM signal:(a) The time domain waveform;(b) the STFT spectrum.The simulation parameters are A=0.1,f0=0,γ=50,φ=0,t1=3,t2=10.

图2 不同尺度系数β=β0 × 10,β0 × 75,β0 × 150,β=β0 ×f1(t) 下的系统参数a1 与实时谱放大因子η 的关系图(仿真参数为b1=1,β0=100,m=2)Fig.2.Curves of η-a1 are obtained under different scale coefficient β=β0 × 10,β0 × 75,β0 × 150,β=β0 ×f1(t).The simulation parameters are b1=1,β0=100,m=2.

为了探究系统参数对最优共振响应的影响,图3 给出了实时谱放大因子η与系统参数a1,b1的伪三维关系图.其中η的大小表示共振响应的强弱程度,η值越大表示共振响应越强,在图形中可以发现明显的共振区域,在这个共振区域内均可发生系统最优共振响应,实现NLFM 信号增强.

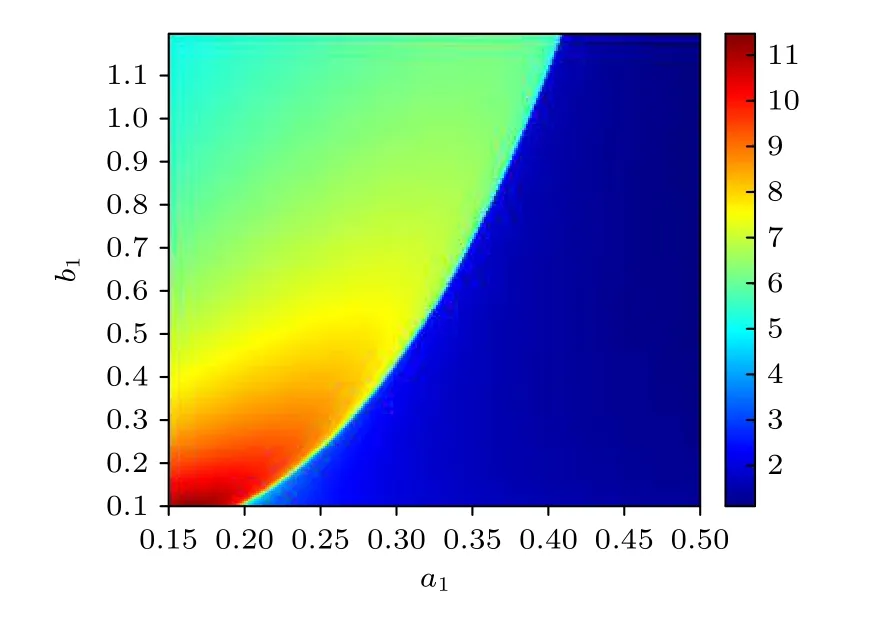
图3 实时谱放大因子η 与系统参数a1,b1 的关系图 (仿真参数为m=2,β0=100)Fig.3.Contour plot of the real time spectral amplification factor η in the a1 -b1 plane.The simulation parameters are m=2,β0=100.

在图2 中,当a1=0.32,b1=1 时,时变尺度方法对应的谱放大因子η取得最大值ηmax=6.4,与其对应的最优系统共振响应如图4 所示.图4(a),(b)分别为响应的时域波形图和STFT 频谱图,信号幅值得到明显增强的同时保证了信号的连续性.

图4 b1=1 时系统的共振输出结果 (a) 时域波形图;(b) STFT 频谱图(仿真参数为m=2,β0=100)Fig.4.The output response of system resonance when b1=1:(a) The time domain waveform;(b) the STFT spectrum.The simulation parameters are m=2,β0=100.

为说明时变尺度方法的必要性,将固定尺度系数变尺度方法和时变尺度系数变尺度方法的最优输出响应进行对比.本文选择固定尺度系数为β=β0× 10,β0× 75,β0× 150,目的是模拟尺度系数较小、适中、较大的情况,尺度变换后信号的频率变为f(t)/β,在图1 中f(t)的范围为0 ≤f(t) ≤ 150,采用固定尺度系数变换后频率范围分别为0 ≤f(t)/(β0×10) ≤ (15/β0),0 ≤f(t)/(β0×75) ≤ (2/β0),0 ≤f(t)/(β0×150) ≤ (1/β0),尺度系数基数β0固定(文中取100),可以发现固定尺度系数为β0×10时,尺度变换后频率达到0.15,此时虽然满足系统共振小参数要求,但是没有达到最优输出效果(见图5),说明尺度变换后的频率需要进一步降低;当尺度系数逐渐增大,尺度变换后的频率逐渐减小,此时针对整个信号均可以满足共振的小参数要求,实现最优系统共振响应.

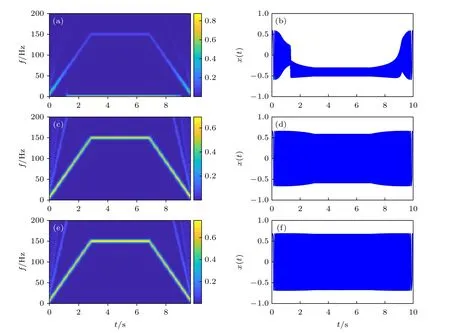
图5 不同的固定尺度系数β 下的系统共振输出结果 (a) β=β0 × 10 下系统输出STFT 谱图;(b) β=β0 ×10 下系统输出时域波形图;(c) β=β0 × 75 下系统输出STFT 谱图;(d) β=β0 × 75 下时域波形图;(e) β=β0 ×150 下系统输出STFT 谱图;(f) β=β0 ×150 下时域波形图 (仿真参数为β0=100)Fig.5.The output response of system resonance under different fixed scale coefficients β:(a) The output STFT spectrum under β=β0 × 10;(b) the output time domain waveform under β=β0 × 10;(c) the output STFT spectrum under β=β0 × 75;(d) the output time domain waveform under β=β0 × 75;(e) the output STFT spectrum under β=β0 × 150;(f) the output time domain waveform under β=β0 × 150.The simulation parameters are β0=100.

图5 为不同固定尺度系数β下的最优系统共振响应结果,当β=β0×10 时,系统最优输出响应变差,在图5(a)中的信号幅值增强效果不显著,图5(b) 的时域波形图中信号波形产生很大失真.当β分别为β0× 75,β0× 150 时,系统共振达到最优输出响应,与时变尺度方法下的最优输出响应区别不大.但是,固定尺度系数下系统最优响应依赖于人为选择的尺度系数,一旦参数选择不理想,共振输出响应会变得很差,而时变尺度方法将系数定为NLFM 信号的离散化频率f1(t),克服了人为选择造成的系数最优输出响应不稳定的缺点.

3.2 调幅-调频NLFM 信号

在信号处理中,由正弦信号频率调制和幅值调制的信号也是一种典型的NLFM 信号,该类信号特点是瞬时频率随时间波动,变化规律复杂,研究这类信号最优系统共振响应及增强具有重要意义.因此,根据文献[29],本文构造了一种调幅-调频的NLFM 仿真信号,如 (11) 式所示:

该仿真信号受到正弦幅值、双正弦频率调制,如图6所示.图6(a),(b) 分别为该信号的时域波形图和STFT 频谱图,不同时刻信号的幅值发生变化,频率也发生变化,频率分布在10—75 Hz.黑色实线为NLFM 信号通过Hilbert 变换相位提取的瞬时频率曲线,与时频特征曲线相一致.对于此类NLFM信号而言,固定尺度变换方法不适用.

图6 输入的NLFM 信号 (a) 时域波形图;(b) STFT 时频图Fig.6.The input NLFM signal:(a) The time domain waveform;(b) the STFT spectrum.

图7 为a1=0.01 时不同尺度系数下实时谱放大因子η与系统参数b1的关系图,在不同的尺度系数下,随着b1的增大,η表现出先增大后减小的规律.对于时变尺度系数β=β0×f1(t),当b1=0.0001,a1=0.01 时,实时谱放大因子最大为101.1.对于固定尺度系数的情况,仅从数值上来看,其谱放大因子既可能比对应的实时尺度系数下共振输出结果小,也可能比其大.

图7 不同尺度系数下的实时谱放大因子η 与系统参数b1 关系图 (仿真参数为a1=0.01,m=5,β0=1000)Fig.7.Curves of η-b1 are obtained under different scale coefficients.The simulation parameters are a1=0.01,m=5,β0=1000.

在时变尺度方法处理下,其对应的最优输出信号如图8 所示.图8(a),(b) 分别为最优系统共振响应时域波形图和STFT 频谱图,信号幅值大幅增强,同时保证信号时频特征的连续性.需要说明的是在图8(b)中短时傅里叶谱能量计算范围,黑色实线包围区间表示响应信号的能量计算区间,该区间内所有STFT 能量值之和作为输出谱能量,输入信号谱能量为NLFM 信号频率曲线上STFT能量值之和.

图8 时变尺度系数下最优共振输出结果 (a) 时域波形图;(b) STFT 频谱图 (仿真参数为m=5,β0=1000)Fig.8.The output response of optimal resonance:(a) The time domain waveform;(b) the STFT spectrum.The simulation parameters are m=5,β0=1000.

虽然在图7 实时谱放大因子η与系统参数b1的关系图中,固定的尺度系数所导致的共振结果η(β=β0×40,β0×75)有的比时变尺度系数共振结果的η大,最优共振结果如图9 所示,但是固定尺度变换方法处理后的NLFM 信号的连续性很差,能量发散现象严重,远没有时变尺度共振效果好.

图9 不同固定尺度系数β 下共振响应 (a) β=β0 × 10 下输出STFT 谱图;(b) β=β0 × 10 下输出时域波形图;(c) β=β0 ×40 下输出STFT 谱图;(d) β=β0 × 40 下输出时域波形图;(e) β=β0 × 75 下输出STFT 谱图;(f) β=β0 × 75 下输出时域波形图Fig.9.The resonance response under different fixed scale coefficient β:(a) The output STFT spectrum under β=β0 × 10;(b) the output time domain waveform under β=β0 × 10;(c) the output STFT spectrum under β=β0 × 40;(d) the output time domain waveform under β=β0 × 40;(e) the output STFT spectrum under β=β0 × 75;(f) the output time domain waveform under β=β0 × 75.