基于四波混频过程的纠缠光放大*

徐笑吟 刘胜帅† 荆杰泰2)3)4)‡

1) (华东师范大学,精密光谱科学与技术国家重点实验室,上海 200062)

2) (中国科学院超强激光科学卓越创新中心,上海 201800)

3) (浙江大学物理学系,杭州 310027)

4) (山西大学,极端光学协同创新中心,太原 030006)

双模纠缠态是量子信息领域一种重要的量子资源,本文基于四波混频过程从理论上提出了对双模纠缠态的单个模式(单模放大方案)和对双模纠缠态的两个模式(双模放大方案)的放大.利用光学分束器模型来模拟在光学传输过程中损耗引入的真空场噪声,利用部分转置正定判据分析了两种不同的放大方案中四波混频过程的增益对初始双模纠缠态的纠缠程度的影响.结果表明,在特定的损耗情况下,两个方案中初始双模纠缠态的纠缠度都随增益的增大而减小,直至消失,且双模放大方案中初始双模纠缠态纠缠消失得比单模放大方案中更快.本文的理论结果为实验上实现基于四波混频过程的双模纠缠态的放大奠定了理论基础.

1 引言

量子纠缠是量子物理中一个十分重要的非经典资源[1],在量子信息领域有着广阔的应用前景[2,3].对于双模纠缠态Einstein-Podolsky-Rosen (EPR),由于两个模式之间存在关联特性,对其中一束光的测量必然会影响另一束光.基于此特性,利用双模纠缠态可以实现一些经典手段无法实现的任务[4-10].因此,双模纠缠态受到了学术界的持续关注,对双模纠缠态的研究在分离变量和连续变量领域取得了一系列研究成果.如1997 年,Zeilinger 研究组[11]利用双模纠缠态在实验上验证了光子的隐形传态.1998 年,Kimble 研究组[12]在连续变量中实现了无条件量子隐形传态.2002 年,彭堃墀教授团队[13]利用光场的正交振幅和正交相位,实现了两组份连续变量高通道容量量子密集编码.

目前已经证明,在85Rb 蒸气池中的四波混频过程是产生双模纠缠态的一项很有前景的技术[14-17].这种四波混频过程在产生双模纠缠态上有很多优势.例如,四波混频过程具有强的非线性相互作用强度,不需要外部腔的耦合,因此具有空间多模的特性.基于以上优点,这种四波混频过程被广泛应用于量子信息[18-20]和量子精密测量[21-23].如2009年,美国Lett 研究组[24]利用四波混频过程实现了EPR 纠缠光束延迟,证明了铷原子池可以作为信息存储器对信息进行短时间存储.2015 年,Pooser研究组[25]利用四波混频过程在两通道之间建立量子关联,实现了表面等离子共振传感器灵敏度的显著提高.同时,基于类原子系综的多波混频过程及基于其他原子系综的四波混频过程也被证明可以用来产生量子压缩[26-29].最近,四波混频过程被证明可以构建一个低噪声放大器[30].然而,通过四波混频构建的放大器放大双模纠缠态并没有被系统地研究.本文从理论上提出了两种方案,第一种方案是四波混频产生双模纠缠态的其中一个模式通过另外一个四波混频过程放大,第二种方案是四波混频产生双模纠缠态的两个模式分别通过两个四波混频过程放大.由于实验中光束在传输过程中会发生损耗,因此有必要在上述两种方案中加入由环境带来的真空场噪声.同时,采用部分转置正定(PPT)判据[31,32]从理论上分析了在特定的传输损耗下,两个方案中放大增益对初始双模纠缠态纠缠特性的影响.证明了在确定的传输损耗下,两种方案中初始双模纠缠态的纠缠特性都随四波混频过程增益的增大而降低,而当增益增大到一定值时初始双模纠缠态的纠缠特性会消失,且在双模放大方案中比单模放大方案中消失得更快.

2 单模放大方案

2.1 理论模型

图1(a) 是对EPR 光束的单个模式进行放大的结构示意图.利用一个频率非简并的四波混频过程产生了一个双模纠缠态并对其中一个模式进行放大.在这里,系统在四波混频过程中发生的损耗可以看成是原光束和真空光束入射到一个光学分束器中引入的真空场噪声.图1(b)是单个四波混频过程的能级图,Δ和δ分别对应单光子失谐和双光子失谐.泵浦光同时驱动了两个基于基态F=2和F=3 的能级跃迁,湮灭两个泵浦光子的同时会产生一个探针光子和一个共轭光子.其中探针光相对于泵浦光具有3.04 GHz 的红移,共轭光相对于泵浦光具有3.04 GHz 的蓝移.在考虑损耗的情况下,第1 个四波混频过程的输入输出关系是[19,33]

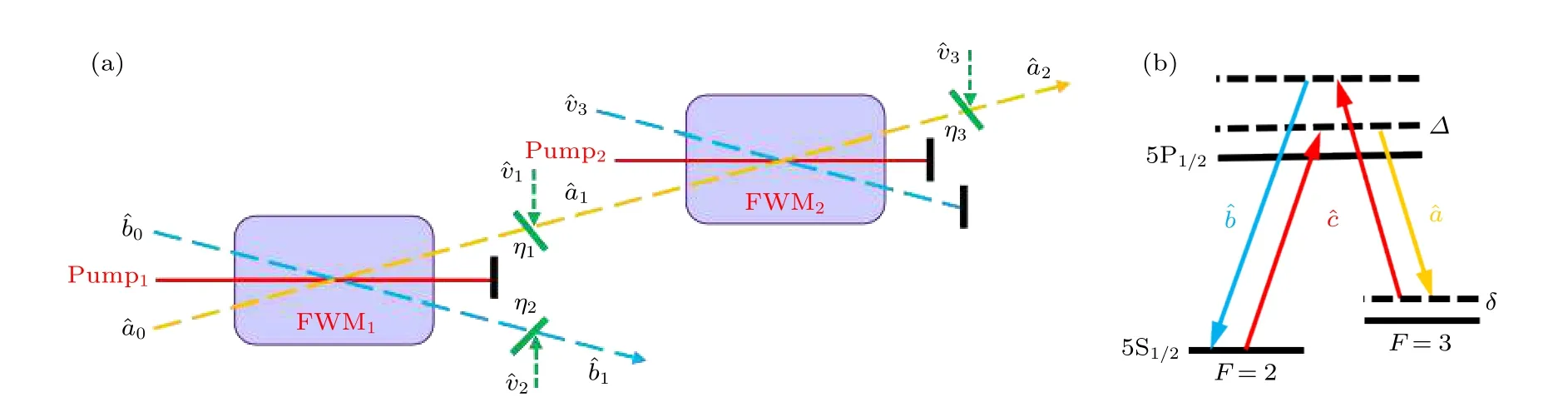
图1 一种对EPR 光束进行单模放大的方案 (a) 对EPR 光束进行单模放大的系统简图;(b) 85Rb D1 线的双Λ 能级结构Fig.1.A scheme for single-mode amplification of EPR beams:(a) Simplified diagram of single-mode amplification of EPR beams;(b) double-Λ energy level structure of 85Rb D1 line.

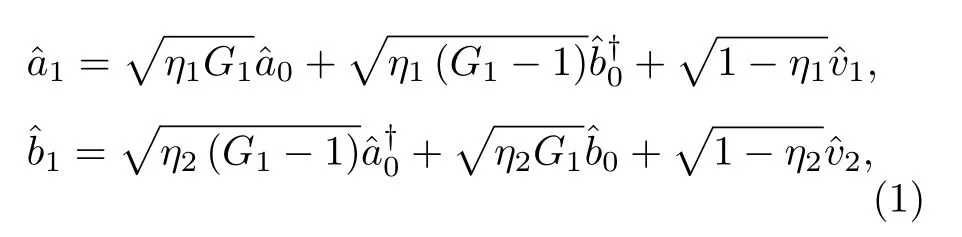
其中G1是第一个四波混频过程(FWM1) 的增益,0和0是真空注入,1和1是第一个四波混频过程产生的探针光束和共轭光束,表示真空场的湮灭算符,η1和η2分别表示1和1的传输效率.接着将探针光束1作为第二个四波混频过程(FWM2)的种子光,与泵浦光束 Pump2注入到第二个热85Rb 蒸气池中,产生放大后的探针光束2.在考虑损耗的情况下,第二个四波混频过程的输入输出关系为

其中G2是第二个四波混频过程的增益,2是放大后的探针光束,分别表示真空场的产生算符和湮灭算符,η3表示2的传输效率.此方案中放大后的探针光束2和原来的共轭光束1是相互关联的,后面会通过研究之间的纠缠度与四波混频过程增益的关系来揭示增益对初始双模纠缠态的影响.

在量子光学中,光场的性质可以用正交振幅算符和正交相位算符来刻画.在这里,分别把正交振幅算符和正交相位算符定义为

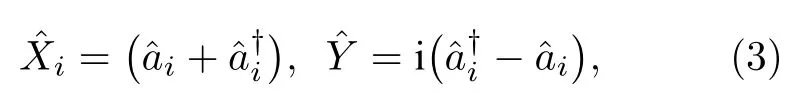
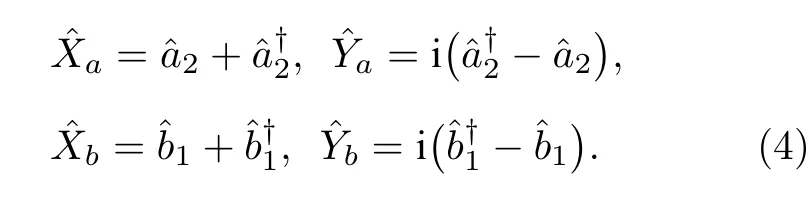
双模纠缠态的量子特性可以完全被协方差矩阵描述,定义正交振幅协方差为,类似地可以得到正交相位的协方差.正交振幅和相位算符又是相互正交的,即.因此,这种单模放大方案输出的关联模式的协方差可以写为

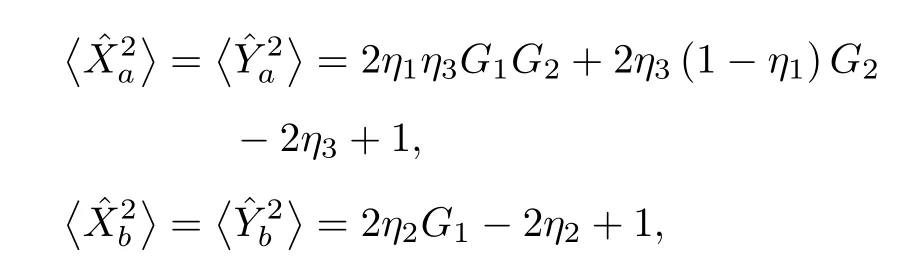
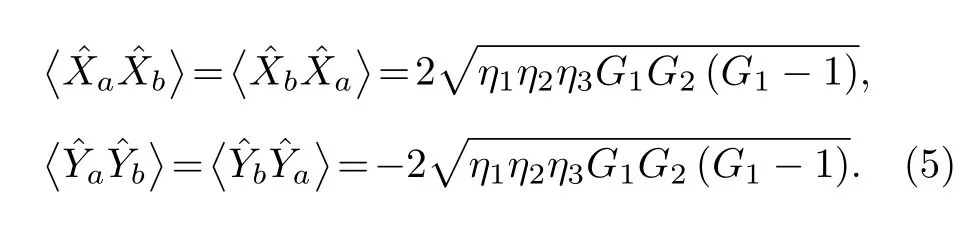
2.2 纠缠特性分析

对于产生两个关联模式的体系,部分转置正定(PPT)判据是一个充分必要的判据,来描述系统的纠缠特性.它被描述为:如果系统的部分转置协方差矩阵的最小辛本征值λ小于1,则存在两个模式之间的纠缠[31,32].而一个包含N个模式的量子态的协方差矩阵是一个2N阶的方阵,因此可以将上述单模放大方案中探针光束和共轭光束的协方差矩阵(σ)写为σ=〈ξξT〉,其中,因此协方差矩阵的表达式为[31,32]

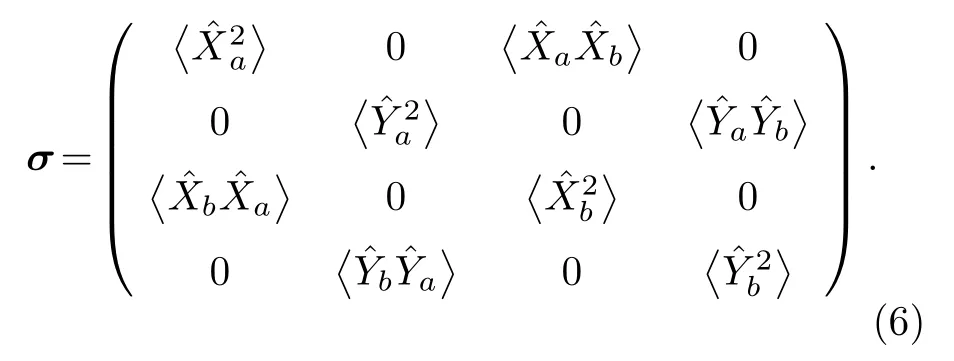
将(5)式代入到(6)式的协方差矩阵中,并对其进行部分转置处理,再求其最小辛本征值.若最小辛本征值小于1,则表明两个输出的关联模式之间存在纠缠.此外,最小辛本征值越小,说明光束之间的纠缠程度越好.由(6)式求出的最小辛本征值与G1,G2,η1,η2和η3有关,表达式为

单个四波混频过程已经被确认可以产生双模纠缠态,即对任何G1＞1,单个四波混频过程产生的EPR 光束的最小辛本征值都小于1.在实验上,探针光和共轭光的传输损耗一般为20% 和10%,因此本文将1,1和2的传输效率分别设定为η1=0.8,η2=0.9和η3=0.8,来模拟实验中光束的传输损耗.下面固定G1,研究2和1两个关联光束的纠缠特性与G2的关系.图2 中的3 条曲线分别是当G1=1.5,G1=2.5,G1=50.0 时将PPT判据应用于光束2和1的最小辛本征值(smallest symplectic eigenvalue).在图2 中,2和1之间的纠缠强度随增益G2的增大而减小.此外还可以看出,当G2增大到一定值后若继续增大,最小辛本征值将大于1,表明在特定的真空噪声影响下,对第一个四波混频过程产生的EPR 光束进行单模放大后,初始双模纠缠态的纠缠性质会随着增益的增大而减小,直至纠缠特性消失.

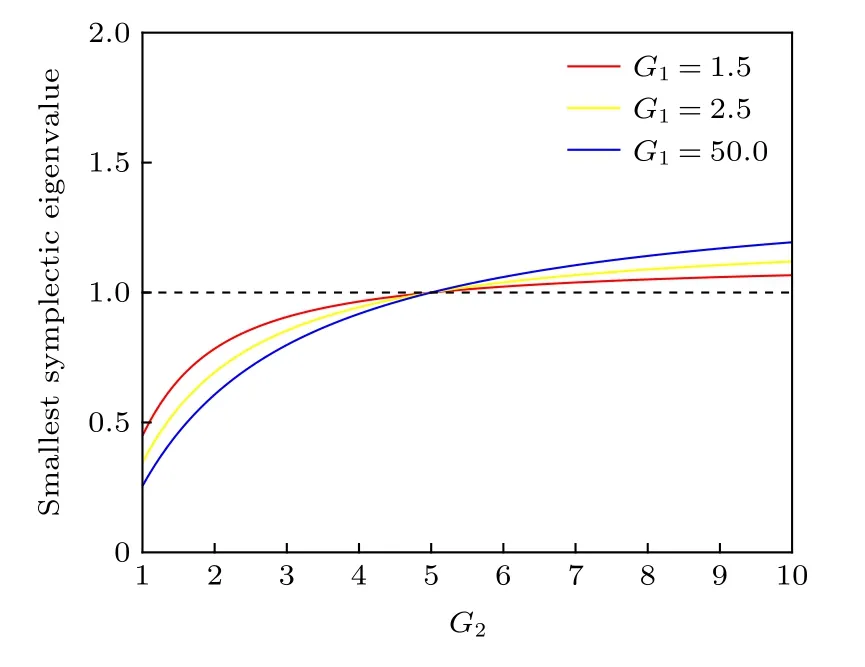
图2 G1不同的情况下单模放大方案最小辛本征值与G2的关系Fig.2.Relationship between the smallest symplectic eigenvalue and G2 of the single-mode amplification scheme under different value of G1.

3 双模放大方案

3.1 理论模型

图3 是对EPR 光束的两个模式分别进行放大的结构示意图.0和0是真空态,与泵浦光束Pump1共同注入到第一个热85Rb 蒸气池中.1和1分别是第一个四波混频过程(FWM1)产生的探针光束和共轭光束.将这两个EPR 光束分别与两个泵浦光束(Pump2和Pump3)作为第二个四波混频过程(FWM2)和第三个四波混频过程(FWM3)的注入,产生了被放大的探针光束2和共轭光束2.令第一个四波混频过程的增益为G1,第二和第三个四波混频过程的增益都为G2.在考虑损耗的情况下,令1,1,2和2的传输效率分别为η1,η2,η3和η4,则这种双模放大结构的输入输出关系为其中2和2分别是被放大的探针光束和共轭光束的湮灭算符,1,2,5和6表示真空场的湮灭算符,表示真空场的产生算符.此方案中放大后的探针光束2和共轭光束2也是相互关联的,2和2之间的纠缠特性在接下来会被研究.

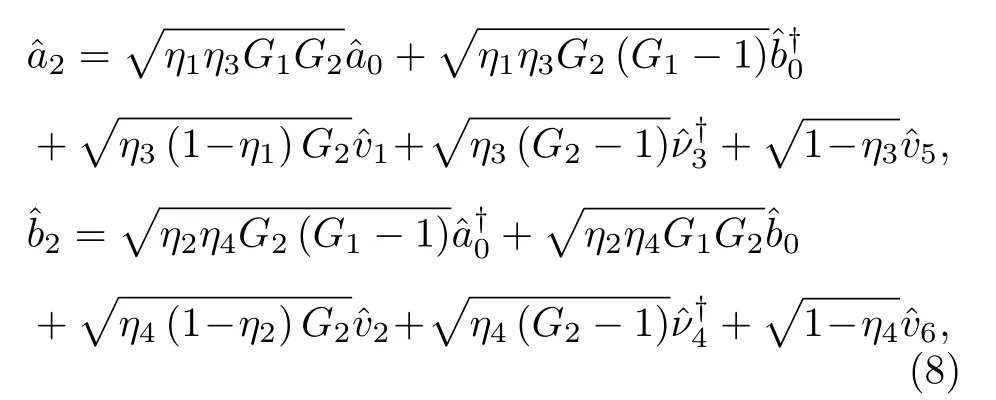
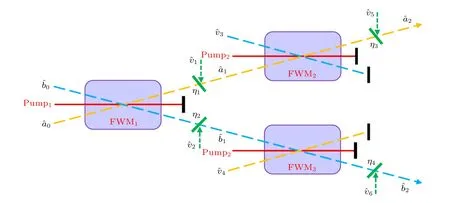
图3 一种对EPR 光束进行双模放大的方案Fig.3.A scheme for two-mode amplification of EPR beams.

3.2 纠缠特性分析

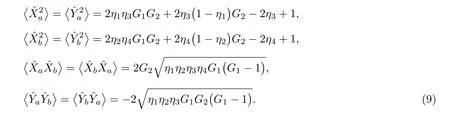
将(9)式代入到(6)式中,并进行部分转置处理,得到的最小辛本征值与G1,G2,η1,η2,η3和η4有关,表达式为

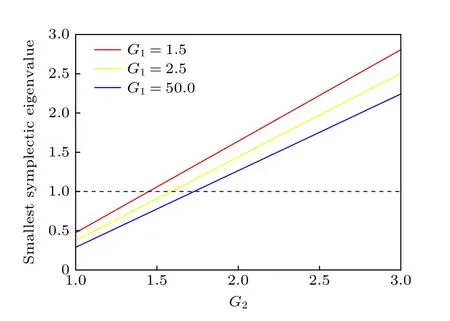
图4 G1不同的情况下双模放大方案最小辛本征值与G2的关系Fig.4.Relationship between the smallest symplectic eigenvalue andG2 of the two-mode amplification scheme under different value of G1.

4 结论

本文基于四波混频过程从理论上提出了对EPR 纠缠光束的其中一个模式进行放大和对两个模式同时进行放大的方案,在考虑放大过程中损耗引入的真空场噪声的情况下,计算分析了两个方案中输出模式的量子纠缠特性.利用部分转置正定判据研究了两个方案的放大增益对初始双模纠缠态纠缠程度的影响.结果表明在特定的真空场噪声影响下,当放大EPR 光束的强度增益处于一定范围内时,单模放大方案和双模放大方案中初始双模纠缠态的纠缠特性可以保持,并且增益越大,纠缠越弱,直至纠缠消失.另外,通过比较两种方案中初始双模纠缠态随增益的变化,可以看出双模放大方案中初始双模纠缠态的纠缠比在单模放大方案中消失得更快.本文的理论计算结果为实验上实现EPR 光束的放大提供了可靠的理论依据.