基于多路可视图的健康与心梗患者心电图信号复杂网络识别*

马志怡 杨小冬† 何爱军 马璐 王俊

1) (中国矿业大学计算机科学与技术学院,徐州 221116)

2) (南京大学电子科学与工程学院,南京 210023)

3) (中国矿业大学信息与控制工程学院,徐州 221116)

4) (徐州 221116 宿州职业技术学院,宿州 234000)

5) (南京邮电大学地理与生物信息学院,南京 210023)

可视图(visibility graph,VG)算法已被证明是将时间序列转换为复杂网络的简单且高效的方法,其构成的复杂网络在拓扑结构中继承了原始时间序列的动力学特性.目前,单维时间序列的可视图分析已趋于成熟,但应用于复杂系统时,单变量往往无法描述系统的全局特征.本文提出一种新的多元时间序列分析方法,将心梗和健康人的12 导联心电图(electrocardiograph,ECG)信号转换为多路可视图,以每个导联为一个节点,两个导联构成可视图的层间互信息为连边权重,将其映射到复杂网络.由于不同人群的全连通网络表现为完全相同的拓扑结构,无法唯一表征不同个体的动力学特征,根据层间互信息大小重构网络,提取权重度和加权聚类系数,实现对不同人群12 导联ECG 信号的识别.为判断序列长度对识别效果的影响,引入多尺度权重度分布熵.由于健康受试者拥有更高的平均权重度和平均加权聚类系数,其映射网络表现为更加规则的结构、更高的复杂性和连接性,可以与心梗患者进行区分,两个参数的识别准确率均达到93.3%.

1 引言

随着大数据的快速发展,每时每刻有数以百万计的信息涌现,多样和复杂的数据给各领域的研究者们带来巨大挑战.其中,时间序列数据引起学者们的广泛关注.2006 年,Zhang 等[1]将伪周期时间序列映射到复杂网络,发现复杂网络作为有效载体可以用于非线性时间序列的动力学分析.此后,复杂网络成为时间序列分析的有效工具,越来越受到学者们的关注[2].2008 年,Lacasa 等[3]提出可视图算法,将时间序列的每一个数据点映射为网络中的节点,节点间是否连接取决于数据点之间的可视性.2009 年,Luque 等[4]在其基础上提出结构更为简化的水平可视图算法,降低其时间复杂度.同年,Marwan 等[5-7]将相空间向量看作节点,通过向量之间的距离定义节点间的连接[8],提出递归网络.2012 年,周婷婷等[9]提出抗噪性能更好的有限穿越可视图.2013 年,Sun 等[10]提出转换网络,主要思想是将时间序列转换为符号表示并将每个符号定义为一个节点,用不同符号之间的转移概率描述节点间的连接性[11,12].

可视图(visibility graph,VG)算法作为应用最为广泛的时间序列转换策略之一,被成功应用于地理学[13,14]、医学[15-20]、金融学[21-23]等各个领域中.然而,随着多传感技术的更新,单层网络对多通道时间序列的融合和复杂系统的描述存在一定的局限性,因此,多元时间序列分析逐渐受到关注[24,25].学者们对此进行大量研究,将注意力转向多层网络,提出从多元时间序列映射到多层复杂网络的诸多方法[26-32].2015 年,Lacasa 等[33]提出多路可视图,开创了基于可视图的多元时间序列分析先河.在此基础上,Rafael 等[34]利用联合分布图分析环境变量间的相关性,证明层间互信息和平均边缘重叠可以描述大气污染物之间的相互作用.Gao等[35]利用多路有限穿越可视图对基于SSMVEP的脑电信号进行分析,成功识别了个体的正常和疲劳行为.Cai 等[36]提出基于模体的多路可视图卷积神经网络,引入多模体熵作为区分不同睡眠阶段脑电图(electroencephalogram,EEG)信号的定量指标.Samanta 等[37]提出基于不同电极间相互关联的聚类系数构建脑连接网络的新方法,采用基于自动编码器的深度特征提取技术从脑连接矩阵图像中提取有效特征,实现对不同运动脑电信号的分类.

心梗(myocardial infarction,MI)是全球范围内致死率最高的疾病之一[38].目前,MI 的临床诊断主要依赖医生对心电信号的经验分析,缺乏更加行之有效的手段.因此,学者们提出基于12 导联分析的MI 自动检测算法.最早的方法是提取心电图中的时频域特征,揭示其演化与心肌梗塞之间的联系.Dohare 等[39]提取12 导联心电图的P 波、QRS波和ST-T 段的幅值、面积、均值、偏度和峰度等特征对MI 信号进行检测.Shanna 等[40]对心电信号进行6 层连续小波分解并将每层小波系数的Renyi熵、分形维数和模糊熵作为特征进行MI 识别.Tripathy 等[41]提出基于傅里叶-贝塞尔级数展开的经验小波变换对多导联心电图进行多尺度分析.随着计算机技术的发展,神经网络成为提取心电图特征的有效工具.Acharya 等[42]提出基于11 层卷积神经网络(convolutional neural network,CNN)的模型,利用Ⅱ导联的心电图(electrocardiograph,ECG)信号准确检测MI.熊鹏等[43]和Liu 等[44]将原始心电信号串联接入数据作为输入,利用神经网络方法进行特征提取从而实现对心肌梗塞的检测.然而,上述检测的方法或仅考虑单维时间序列,忽略了12 导联的多样性,或将12 导联以串联方式送入网络,忽略了多导联之间的内在联系.针对以上不足,本文提出多路可视图方法,将12 导联中的每一个导联作为多路可视图的一路,映射为一个网络节点,节点之间的层间互信息作为连边权重,并引入阈值构造无向加权网络,提取权重度和加权聚类系数两个参数,实现对MI 疾病的检测.该方法以受试者12 导联作为研究对象,利用多路可视图对其进行联合分析,以研究心脏电系统的非线性动力学特征,对MI 患者的检测和诊断具有重要意义.

2 多路可视图

2.1 构造方法

首先回顾一维可视图的构造[3].VG 算法的主要思想是将时间序列中的每一个数据点映射到复杂网络的一个节点,节点间有无连边取决于两节点是否满足可视性准则:对于任意两点ta,tc,若它们之间的连线没有被任何位于这两点之间的其他点所截断,则这两个节点“可视”,在复杂网络中可以连接成边,相邻两节点间一定“可视”.VG算法的公式描述为

其中,tb是位于ta,tc之间的任意节点.

多路可视图的构造建立在一维可视图基础之上,若将多元时间序列看作是多维的,则每个单变量时间序列为其中的一维.我们考虑一个M维实值序列其中,上标对应序列所在维数,N代表序列长度,每一维时间序列的长度相同.对每个单变量时间序列,根据VG 算法构造可视图网络,将M维时间序列全部映射完成后构造的具有M层复杂网络的结构,即为多路可视图.图1 以三维时间序列为例,描述了一个三路可视图的构造过程[33].多路可视图用其邻接矩阵向量A={A[1],···,A[α],···,A[M]}表示,其中,对于第α层的邻接矩阵,当且仅当节点i和节点j在第α层连接时,.每一个节点i对应一个度向量ki,

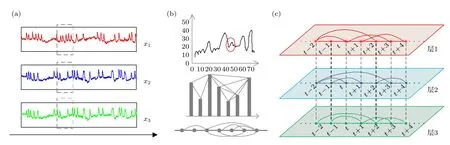
图1 VG 算法构造多路可视图示意图 (a)一个多维时间序列;(b) VG 算法示意图,从上至下依次为原始时间序列、红色圆圈包含片段的VG 算法过程及其构造后的网络;(c)图(a)虚线框所含序列通过VG 算法构造的多路可视图,其中层1,2,3 分别对应时间序列x1,x2,x3Fig.1.Schematic diagram of constructing multiplex visibility graph using VG algorithm:(a) a multivariate time series;(b) schematic diagram of VG algorithm.From top to bottom are original time series,VG algorithm procedure for fragment contained in the red circle and the constructed network;(c) multiplex visibility graph of series in dotted box in figure (a) constructed by VG algorithm,where layers 1,2 and 3 correspond to time series x1,x2 and x3,respectively.

2.2 多路可视图映射到复杂网络

2.2.1 层间互信息

用层间互信息Iα,β[33]量化多路可视图不同层之间度分布的相关性,I表示为

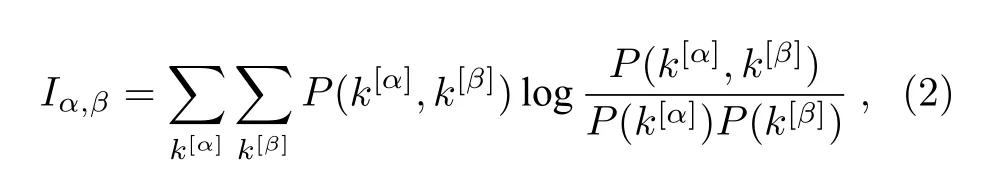
其中,α,β是多路可视图中的任意两层,对应时间序列的度分布分别为P(k[α])和P(k[β]),P(k[α],k[β])是在第α层寻找度为k[α]的点和在第β层寻找度为k[β]的点的联合概率,计算方法为

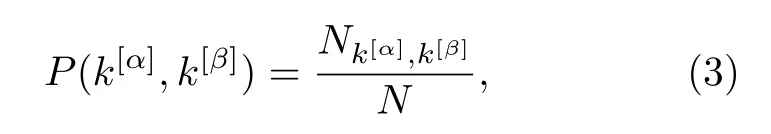
其中,N为每一层的序列长度,Nk[α]k[β]是在第α层和第β层上度值分别等于k[α]和k[β]的节点数

层间互信息Iα, β量化了同一节点在两个不同层之间度的相关性,Iα, β值越大,两层之间的度分布越相关,因此时间序列的结构也越相关,表明两个时间序列可能具有更加相似的行为.

对于图1 中所描述的三路可视图,将其每层视为网络中的一个节点,两层之间的层间互信息I作为节点间连边的权重,则该多路可视图被映射为具有三个节点的无向加权网络,且该网络是全连通的.映射后的网络如图2 所示.

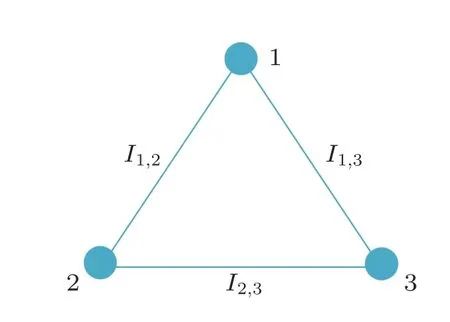
图2 多路可视图映射后的网络.节点1,2,3 对应多路可视图的第1 层、第2 层和第3 层.I1,2,I1,3,I2,3 分别为层1 和层2、层1 和层3、层2 和层3 之间的互信息,同时为对应两点连边的权重Fig.2.Network mapped by multiplex visibility graph.Nodes 1,2 and 3 correspond to the 1st,2nd and 3rd layers of multiplex visibility graph.I1,2,I1,3,I2,3 are the mutual information between layer 1 and layer 2,layer 1 and layer 3,layer 2 and layer 3 respectively,meanwhile,they are the weight of edges of corresponding two points.

2.2.2 权重度分布熵

权重度分布熵[45]表征复杂网络的拓扑结构信息,反映网络的连接复杂度.当网络的连边较多、结构更为规则时,其权值分布较均匀,表现为权重度分布熵较大;反之,当连边较少、结构不规则时,复杂网络的平均度较小,某些权值高频出现,权重度分布熵较小.节点i的权重度分布熵表示为

式中,a(i,j)表示节点i和节点j连边权重的概率分布,公式为

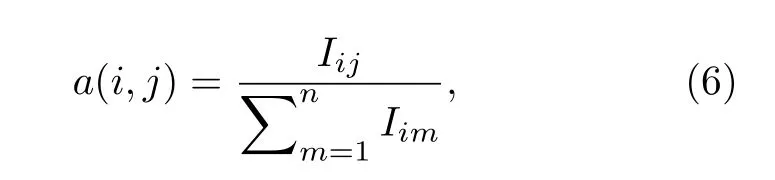
其中,Iij为多路可视图的第i层和第j层之间的层间互信息,根据映射准则,在将多路可视图映射为复杂网络时,其表示节点i和节点j之间的权重.为便于理解、阅读方便,以下在提到节点i和节点j之间的权重时均用wij表示.n代表与节点i相连的节点数.

具有N个节点的加权网络的平均权重度分布熵可表示为

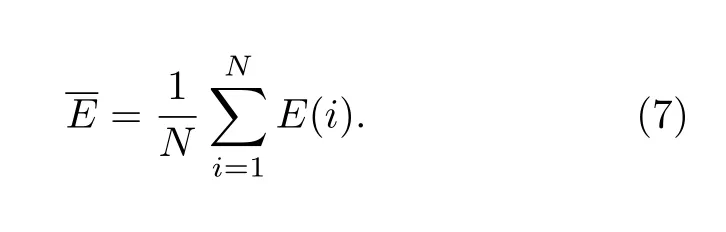
312 导联ECG 信号的多路可视图

3.1 数据描述

我们将本文多路可视图运用到12 导联ECG信号的分析中.数据来自PhysioNet 网站(https://www.physionet.org)的PTB 心电数据库.PTB 数据库是由德国国家计量学会提供的ECG 数据库[46],该数据库包含52 名健康人及238 名不同疾病患者(其中包括148 名MI 患者、18 名心力衰竭患者、15 名束支性传导阻滞患者、14 名心律失常患者以及少数其他疾病的患者),每个人对应1—5 条记录,每条记录包含12 导联ECG 信号(3 个肢体标准导联Ⅰ,Ⅱ,Ⅲ,3 个加压肢体导联avr,avf,avl 和6 个胸导联v1—v6),表1 描述了该12 导联在检测心脏疾病时控制的具体位置.PTB 心电数据库使用的采集设备由14 个用于ECG、1 个用于呼吸以及1 个用于线路电压的通道组成,输入电压为 ± 16 mV,补偿偏置电压为 ± 300 mV,分辨率为16 位,每个采样值为2 个字节,采样频率为1 kHz.

表112 导联名称及其对应的心脏位置Table 1.Name of the 12-lead and their corresponding cardiac location.

我们选取PTB 数据库中健康人和MI 患者的12 导联ECG 信号进行分析,所有的MI 患者数据中,除去无年龄信息的受试者外,有26 名70 岁以上的MI 患者没有与之年龄匹配的健康人群,有13 名30 岁以下的健康人群没有与之匹配的MI 患者.将剩余的所有受试者根据年龄分为4 组,4 组受试者的年龄范围分别为60—69 岁(包含7 名健康受试者和47 名MI 患者)、50—59 岁(包含11 名健康受试者和30 名MI 患者)、40—49 岁(包含6 名健康受试者和23 名MI 患者)和30—39 岁(包含10 名健康受试者和4 名MI 患者).PTB 数据集已对心电信号进行预处理,所以在本研究中,无需对数据进行再次处理.将每个受试者的12 导联数据片段各选择其5000 个顺序数据点进行实验.

3.2 多尺度分析

Costa 等[47]提出时间序列多尺度粗粒化的方法.对于一个长度为N的时间序列{x(i),i=1,2,···,N},根据粗粒化过程定义时间尺度,得到粗粒化时间序列{ys(j),j=1,2,···,N/s},即

其中,s代表尺度因子,N为原始时间序列长度.粗粒化的时间序列长度等于原始序列长度N除以尺度因子s.当s=1 时,序列y(1)与原始序列等值.

我们首先对两类人群原始12 导联ECG 信号进行粗粒化,初始序列长度为N=5000,尺度因子s的取值范围为1—50.经实验,当尺度因子选择过大即序列长度很短时,所采集的信号不能准确反映受试者的心脏状态.在不同尺度因子s下,分别将获得的新序列构成多路可视图,并映射到复杂网络,提取平均权重度分布熵.

计算每组数据中健康人和MI 患者的平均权重度分布熵,结果如图3 所示.

图3 描述了4 组不同年龄阶段的健康人与MI 患者在尺度因子增大时平均权重度分布熵的变化情况.由于短序列更容易产生相似的度分布,两层之间拥有更大的互信息值,全连通网络的权重分布更加均匀,因此,随着尺度因子s在1—10 范围内的增加,两类人群的平均权重度分布熵均明显增大,但当序列粗粒化到一定程度时,该变化消失,平均权重度分布熵值保持稳定.

图3 不同年龄的健康人和MI 患者在不同尺度因子s 下平均权重度分布熵 (a) 60—69 岁;(b) 50—59 岁;(c) 40—49 岁;(d) 30—39 岁.绿色实线为两类人群平均权重度分布熵按比例缩放后的差值,星号表示差值最大处Fig.3.Average weighted distribution entropy of healthy people and patients with MI under different scale factor s:(a) 60—69 years old;(b) 50—59 years old;(c) 40—49 years old;(d) 30—39 years old.The solid green line is the difference of average weighted distribution entropy of two groups after scaling,and asterisk represents the maximum difference.

观察图3 中的差值曲线,对于不同年龄阶段的两类人群,当s取值约为1—10 时,随着尺度因子的增加,平均权重度分布熵的差值曲线呈下降趋势,而此曲线在s大于10 时出现波动.因此,健康人和MI 患者的12 导联ECG 信号在短序列下的识别较为困难.此外,我们发现,当s为1—10 时,不同年龄阶段健康受试者的平均权重度分布熵总是大于MI 患者,表明健康受试者对应复杂网络的权值分布更为平均,拥有更加规则的结构.

4 重构网络

全连通网络具有完全相同的网络拓扑结构,无法对两类人群12 导联ECG 信号的潜在动力学结构进行直观判断.因此,我们引入阈值,重构映射网络.由于重构网络的结构对于每一个个体都是唯一的,并且在不同人群之间存在较大差异,可以提供一种更加简单和直观的方法来描绘复杂系统中不同的动力学特性.

4.1 构造方法

因为连边权重由多路可视图的层间互信息决定,定义阈值为最大层间互信息值的常数倍.对于初始全连通网络,当网络中两点的连边权重I小于给定阈值时,删除该权重对应的连边.否则,保留该连边.如果常数c取值过小,阈值也相应的取较小值时,两类人群的重构网络中小于给定阈值的权重寥寥无几,删去有限连边后,两类人群的重构网络仍然是近似全连通的,网络参数差异较小.因此,令c的取值范围在0.4—0.9 之间.为了获得更加精确的阈值区间,我们将c的步长设置为0.01.

基于以上考虑,定义阈值计算公式为

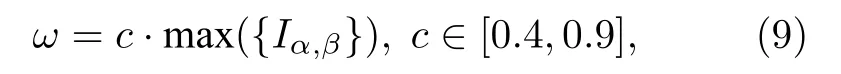
其中,{Iα, β}是多路可视图中所有层间互信息值的集合,c为常数,表示倍数.通过调节c的大小,可以获得最优的阈值区间.

常数c的取值决定了重构网络中连边的数量,12 导联代表的节点之间度分布的相关性取决于每两个节点之间的层间互信息.通过重构网络,部分连边被删除,这一相关性表现在代表12 个导联的节点属性上.因此,我们提取描述节点属性的平均权重度〈d〉.平均权重度越大,表明该导联与其余导联之间的度分布相关性越高.复杂网络平均权重度〈d〉的计算公式为

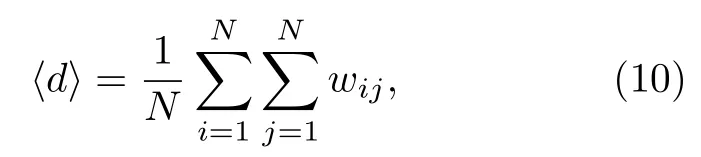
wij为节点i和节点j之间的权重,N代表节点总数.

在不同阈值下,分别对健康受试者和MI 患者的全连通网络进行重构,并计算重构网络的平均权重度,结果如图4 所示.寻找使两类人群平均权重度差值最大的阈值区间,在此区间内,两类人群重构网络的潜在动力学特征差异最为明显,识别效果最佳,因此可以进一步精确阈值范围.

根据图4 可以发现,随着常数c的增大,MI 患者和健康人群平均权重度均逐渐减小并接近0.这是由于当倍数c取值较大时,阈值对应为较大值,导致多数连边被删除,网络拓扑结构中易产生孤立点.此外,我们发现,不同年龄阶段健康人群的平均权重度总是大于MI 患者,表明健康人的重构网络具有更加规则的结构,与图3 所得结论相呼应,证明健康人对应的多路可视图网络具有更高的复杂性和连接性.

为了精确阈值区间,我们在图4 中做出两类人群平均权重度的差值曲线.可见,当常数c在0.67范围以内时,MI 患者和健康人群平均权重度〈d〉的差值曲线基本保持稳定.c较大时,两类人群平均权重度的差距逐渐减小,即网络拓扑结构越来越相似.表2 列出了3.1 节中4 组健康人与MI 患者在平均权重度差值最大时的常数c值.根据表2 中的数据并结合图4 得出,当倍数c取值范围为0.43—0.67时,健康人和MI 患者对应重构网络的平均权重度差异明显,网络拓扑结构上的差异也最为显著.

表24 组健康人-MI 患者对应重构网络的平均权重度差值最大时的常数cTable 2.Constant c of four groups when difference of average weighted degree of reconstructed network being maximum.

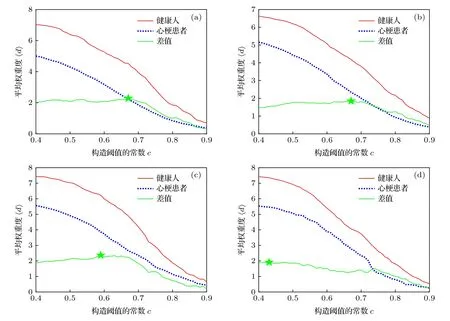
图4 不同年龄组健康受试者与MI 患者在常数c 不同取值时的平均权重度 (a) 60—69 岁;(b) 50—59 岁;(c) 40—49 岁;(d) 30—39 岁.绿色实线为两类人群平均权重度的差值,星号表示差值最大处,其值见表2Fig.4.Average weighted degree of healthy subjects and myocardial infarction patients at different values of constant c:(a) 60—69 years old;(b) 50—59 years old;(c) 40—49 years old;(d) 30—39 years old.The solid green line is the difference of the average weighted degree of two groups,and the asterisk represents the maximum difference,see Table 2 for specific values.

4.2 拓扑结构

为探究12 导联ECG 信号的潜在动力学特征,作出重构网络拓扑图.由4.1 节可知,当c取值在0.43—0.67 范围内时,两类人群的网络参数存在显著差异.由于c=0.43 时可删除最少的连边重构网络,其与原始网络的结构最相似.因此,我们取0.43 作为c值,计算阈值并重构网络,健康人和MI患者的网络拓扑图如图5 所示.通过观察,两类人群的网络拓扑结构存在显著差异.健康受试者的网络拓扑图拥有更加复杂的结构,节点连接更为紧密,表明健康人多路可视图的层间互信息较大,12导联ECG 信号之间具有更加相似的结构;而MI患者对应的网络拓扑图节点之间的连接相对稀疏,甚至出现对应导联i 和导联avr 的两个孤立节点,这两个导联与其他导联的度分布相关性较低.

图5 常数c=0.43 时重构网络的拓扑图 (a)健康受试者;(b) MI 患者.各节点对应的导联已在图中标明.节点大小和颜色对应该节点的权重度.图右侧颜色柱表示节点权重度Fig.5.Topology of the reconstructed network of (a) healthy subjects and (b) patients with MI at c=0.43.The corresponding leads of each node have been indicated in the figure.Size and color are relative to the weighted degree of the node.The color bar on the right of the figure indicates the value of weighted degree.

此外,网络拓扑图中节点的颜色和大小与该节点权重度成正比,计算公式为

其中,wij代表节点i和节点j之间的权重,N代表节点数目.

由图5 可以看出,无论健康人还是MI 患者,胸导联的权重度均大于肢体导联,在进行ECG 信号识别时起到关键作用.胸导联由于距离人体心脏更近,对心脏电活动的反应更为强烈.因此,在对MI 进行检测时,这6 个导联是需要重点关注的对象.对比图5(a)和图5(b),健康受试者和MI 患者的v5,v6 导联对应节点的大小和颜色差异最大,我们或可以据此联合表1 判断,MI 对该患者的左心室影响较为严重.因此,网络拓扑图或为MI 定位提供新的思路,然而,其实际效果及判断准确率等仍需进一步的论证.

4.3 参数分析

为进一步研究两类人群重构网络的拓扑结构,我们计算重构网络的平均权重度〈d〉(见(10)式)和平均加权聚类系数Cw,其中Cw量化了网络的连接性,反映网络微观结构的规则性,计算公式为

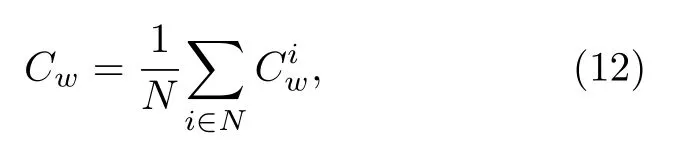
其中,N代表网络中的节点数,是每个节点i的加权聚类系数,即

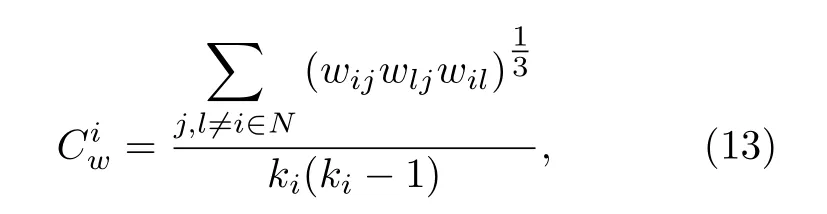
其中,ki为节点i的度,wij,wlj,wil分别代表节点i,j,节点l,j以及节点i,l之间的权重值.为避免实验偶然性,我们对4 组健康人与MI 患者数据进行实验并作出箱图(图6),对结果进行t检验,发现P值远小于0.05,证明健康受试者和MI 患者的平均权重度和平均加权聚类系数之间存在显著差异.

根据图6 我们可以得出,相较MI 患者,健康受试者拥有更高的平均权重度和平均加权聚类系数.从混沌理论的角度来看,心脏作为自然界中最为复杂的非线性系统之一,人体各系统的耦合作用使得心电信号呈现连续的上下波动,形成复杂的时间序列.MI 患者由于心脏部分衰竭导致功能丢失,其复杂性与正常人相比降低,该结论与本文一致.此外,由于MI 患者心脏功能减弱,在不同心肌位置测得的心电信号表现为形态各异的结构,构成多路可视图后的层间互信息较小,在重构网络时,有更多的连边被删除.因此,MI 患者对应复杂网络的连接性低,且各节点拥有较小的权重度.

图6 健康人和MI 患者在最佳阈值下的(a)平均权重度和(b)平均加权聚类系数.第1 组—第4 组受试者的年龄范围分别为60—69 岁、50—59 岁、40—49 岁以及30—39 岁Fig.6.(a) Average weighted degree and (b) average weighted clustering coefficients of healthy and myocardial infarction patients under optimal thresholds.Subjects in groups 1—4 correspond to ages of 60—69 years old,50—59 years old,40—49 years old and 30 to 39 years old respectively.

4.4 与其他方法对比结果

为了评价所提出算法的性能,将MI 信号作为正样本,健康信号作为负样本,并使用平均权重度和平均加权聚类系数两个指标进行分析,计算敏感性(sensitivity,SE)、特异性(specificity,SP)和准确率(accuracy,AC),有

式中,TP,FN,TN,FP 表示分类正确的正样本个数、被错误分类为负样本的正样本个数、分类正确的负样本个数以及被错误分类为正样本的负样本个数.分类准确率代表了该算法对两类样本的总体分类正确率.

本文提出的基于多路可视图的MI 检测方法与现有的MI 检测方法结果进行了对比,基于PTB数据集的对比结果如表3 所示.由表中数据可知,本文方法提取的参数权重度和加权聚类系数分别取得了94.4%,95.83%的敏感性和88.24%,82.35%的特异性,相比文献[48-50]中的检测方法,本文仅在特异性参数上低于Sun 等[49]提出的使用5 阶多项式拟合,确定74 维特征空间,然后应用粒子群优化器将权重建模为高斯分布后进行分类的方法.相比文献[48]中将多导联数据分别使用HMM提取特征后堆叠特征,本文考虑了多导联间的关联性,利用关联指数层间互信息将其构造为网络后进行特征提取,仅使用了一个网络特征即完成了MI的检测,在使用特征个数上优于已有方法,尤其较文献[50]中进行10 个特征融合有了较大的提升.综上,本文方法相较已有方法存在优势,且分类准确率更高,达到93.3%,能够实现MI 的有效检测.

表3 本方法与其他现有方法的比较Table 3.The comparison between proposed method and other existing methods.

5 结论

本文将12 导联ECG 信号构造为多路可视图,通过层间互信息将其映射到复杂网络,为分析12 导联信号的多尺度特征,我们计算网络的多尺度权重度分布熵,发现其可以用作检测MI 患者的有效工具.然而,由于全连通网络具有完全相同的网络拓扑结构,无法唯一表征不同个体的动力学特征,因此,我们对映射网络进行重构.计算重构网络的平均权重度和平均加权聚类系数的结果表明,与健康人群相比,MI 患者的重构网络具有更低的复杂性和连接性,此方法在PTB 数据库上的分类准确率达到了93.3%,实现了对MI 患者和健康人群的有效分类.此外,我们发现,随着患者年龄的增加,其重构网络平均权重度的均值减小,表明老年患者的重构网络拥有更低的边权重,12 导联之间相似的动力学行为减少,患病更加严重.因此,老年MI 患者的诊断和治疗亟需我们的关注.

多路可视图为多元时间序列分析提供了一种新颖、准确且易于扩展的方法.通过计算一些基础的多路参数,如层间互信息和平均边缘重叠,可以对多元时间序列进行联合分析,获取不同状态序列之间的内在联系,以实现对动力学系统的非线性动力学特性进行完整而全面的分析.此外,在使用多路可视图方法进行多元时间序列分析时,可以任意选择变量个数,这使得多通道联合分析变得更加灵活和高效.然而,本文在识别单维时间序列的内在特征时存在局限,仅关注了不同序列之间的整体相似性,因此,我们期待满足反映复杂系统时间演化和表征时间序列局部波动的新的映射方法的提出.