基于改进GA的周期长码直扩信号PN码估计
2022-03-17王自维姚志成王海洋李昱婷
王自维,姚志成,王海洋,李昱婷,侯 范
(火箭军工程大学,西安 710000)
0 引言
直接序列扩频(DSSS)通信被广泛应用于军事和民用通信,具有信息容量大、抗干扰能力强及功率谱密度低等诸多优点。但是这些特性也给通信侦察和电子对抗带来了很大的难度,在非协作通信中,只有估计出对方发射信号的相关参数才有可能实时有效地干扰或破解通信信息[1-2],因此对DSSS信号的检测和参数估计的研究具有重要意义。
一般地,基带DSSS信号的基本参数包括:PN的周期、码元宽度、PN码与信息码同步点以及PN序列等。如果估计到DSSS信号的扩频码序列,就可以说信号实现了完全估计[3]。常见的DSSS信号模型包括短码和长码调制两种类型,其中,短码调制是指一个信息码由一周期的扩频码来调制,长码调制是指将多个信息码调制到扩频码上。
目前,对短码的估计比较成熟。文献[4]提出了用特征分解法来估计PN码;文献[5]利用两个信息码做特征分解,解决了PN码序列相位模糊和失步点估计的不确定性,可以精确估计PN码序列;文献[6]将压缩投影逼近子空间跟踪算法,用于DSSS信号的主特征向量提取,估计出PN码;文献[7]在DSSS信号特征分析的基础上,利用带约束的Hebbian准则,实现了PN码的估计,这也是利用神经网络估计PN码的开端。
对于长码的估计,大多数方法是将观测到的数据按信息码分段后用估计短码的方法来估计每一段的伪码序列,然后进行拼接。文献[8]提出了以两个信息码元宽度为分段长度,然后用特征分解法对PN码序列进行初步估计,并对各段估计序列进行拼接,再通过基于移位相加特性的信息码剥离算法实现PN码序列的盲估计;文献[9]提出一种分段子空间跟踪算法,使用滑动窗口法获得同步信息,并采用子空间跟踪算法分段估计PN码序列,最后依次拼接获得原始信号的PN码序列;文献[10]提出一种基于谱范数和快速子空间跟踪算法,该算法首先对接收信号按信息码宽进行分段,通过信号分段协方差矩阵谱范数对取得码同步,然后用快速约束投影逼近子空间跟踪算法技术估计各段PN序列;文献[11]首先利用分段特征值分解估计出PN码片段并进行拼接,其中每个片段都会独立地取正负号,然后利用梅西算法得到PN码的生成多项式。
本文提出一种基于改进GA的长码估计方法。首先,利用观测信号的协方差谱范数获得信号与伪码的同步点,然后,在同步的基础上截取一个伪码周期的观测数据,并利用改进的GA来估计PN码序,此方法减少了按信息码分段拼接的步骤,降低了复杂度。仿真结果表明,利用改进后的GA,减少了迭代次数,加快了收敛速度,在低信噪比下误码率较小。
1 信号模型
DSSS信号为BPSK调制类型,通过符号序列和PN序列相乘,实现信号扩频。假设其PN码周期、符号周期和码元速率已知,其基带信号模型可以表示为
(1)
(2)
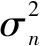
2 算法原理
2.1 谱范数同步算法
首先在观测数据中截取一个信息码长的数据,然后间隔一个PN码周期再截取一个信息码长的数据,截取N段,得到数据矩阵yj,如图1所示。
图1 数据截取模型Fig.1 Data interception model
数据矩阵yj可表示为
(3)
式中:j=1,2,…,k;G为信息码的长度。
然后求yj的协方差矩阵R,即
(4)
延时点τ≠0,表示非同步情形,如图2所示,观测窗口中的数据是由相邻两个信息码中的部分PN码拼接而成的。

图2 数据观测窗口Fig.2 Data observation window
当按照一个信息码序列长度滑动数据窗时,如果信号取得同步,其协方差的谱范数||
y0||
2取得最大。延时点估计值可表示为
(5)
式中,λmax表示求取R的最大特征值。
2.2 适应度函数
适应度函数用来对种群中个体的适应性进行度量,依此决定个体遗传机会的大小。
本文中,将观测信号与种群中个体的乘积作为适应度函数,其表达式为
f(yp′)=yp′·yp=yp′·(sp(t)+n(t))=yp′·sp(t)+yp′·n(t)
(6)
式中:yp′表示估计的PN码序列;yp表示观测信号;sp(t)表示长度为p的直扩信号。本文所用噪声信号为高斯白噪声,可认为噪声与PN码不相关,即yp′·n(t)的值为零。所以只有估计值与PN码序列相一致时或相反时适应度值才会达到最大,从而将求PN码序列问题转化为求最优解问题。
2.3 GA改进
GA是求解复杂优化问题的一种有效方法,具有全局收敛性、鲁棒性,已得到较广泛应用,主要包括初始化种群、选择、交叉、变异、终止条件判决等几个步骤。首先,通过初始化随机产生种群个体,然后,选择适应值较大的个体进行交叉变异,最后,判断是否达到终止条件,若已达到,则此时适应值最大的个体是最优解,若未达到,则继续进行选择交叉变异操作直到满足终止条件为止。
简单遗传算法估计长码时,具有“早熟”现象,易收敛到局部最优解且收敛速度慢。“早熟”现象的根本原因是未得到最优解之前,群体丧失了多样性而提前收敛到局部最优解[12]。针对以上问题提出以下改进方法。
2.3.1 改进初始值的选取
一般的GA,初始种群是随机选取的,初始种群的覆盖空间具有很大的不确定性,导致收敛速度很慢。因为在观测信号中包含了伪码的信息,所以本文根据观测信号来初始化种群。
2.3.2 改进交叉变异策略
通常在GA中依靠交叉变异来更新种群,由于在交叉变异过程中可能使当前适应值最大的个体更加接近最优值,也可能使其适应度值变小,所以保留适应度值最大的个体,避免其参与交叉变异。如果更新的种群中有比其适应度值更大的,那么将其替换。
在GA中将交叉概率和变异概率设为固定值,它的选取对收敛速度也有很大影响,本文根据适应度值的大小来自适应地选取交叉概率和变异概率,适应度值较大的个体在进行交叉变异时,交叉概率选择大一点,变异概率选择小一点,适应度值小的个体则相反。
在GA中选择出一部分适应度值较大的个体进行交叉变异,淘汰掉适应度值较小的个体,这样很容易收敛到局部最优解,为避免陷入局部最优,种群更新时加入一部分新生个体,相当于在全局范围内搜索最优值。
综上所述,用GA估计PN码序列的步骤如下所述。
1) 初始化种群。在观测信号的每一个码元中随机选取一个点,得到一个长度为P的个体,选取N组数据,构成含有N个个体的种群。
2) 计算适应度值。根据适应度函数计算每一个个体的适应度值,淘汰掉一部分适应度值较小的个体。
3) 交叉变异。保留步骤2)中适应度值最大的个体,选取适应度值较大的一部分个体进行交叉操作,然后再选取其中的一半进行变异。
4) 种群更新。将经过步骤3)的个体作为新种群的一部分,然后再加入一部分新生群体。
5) 终止条件。如果未达到终止条件,重复步骤2)~4),如果达到了终止条件,此时适应度值最大的个体便是估计的扩频码序列。
3 实验仿真
3.1 实验1
周期长码直扩信号采用BPSK调制,扩频码序列采用63 bit的平衡m序列,码速率为1 Mibit/s,信息码长度分别设为21 bit,信息码速率为0.047 6 Mibit/s,采样频率为1 MHz,信噪比为-10 dB,周期长码中谱范数的延时点τ的估计效果见图3。
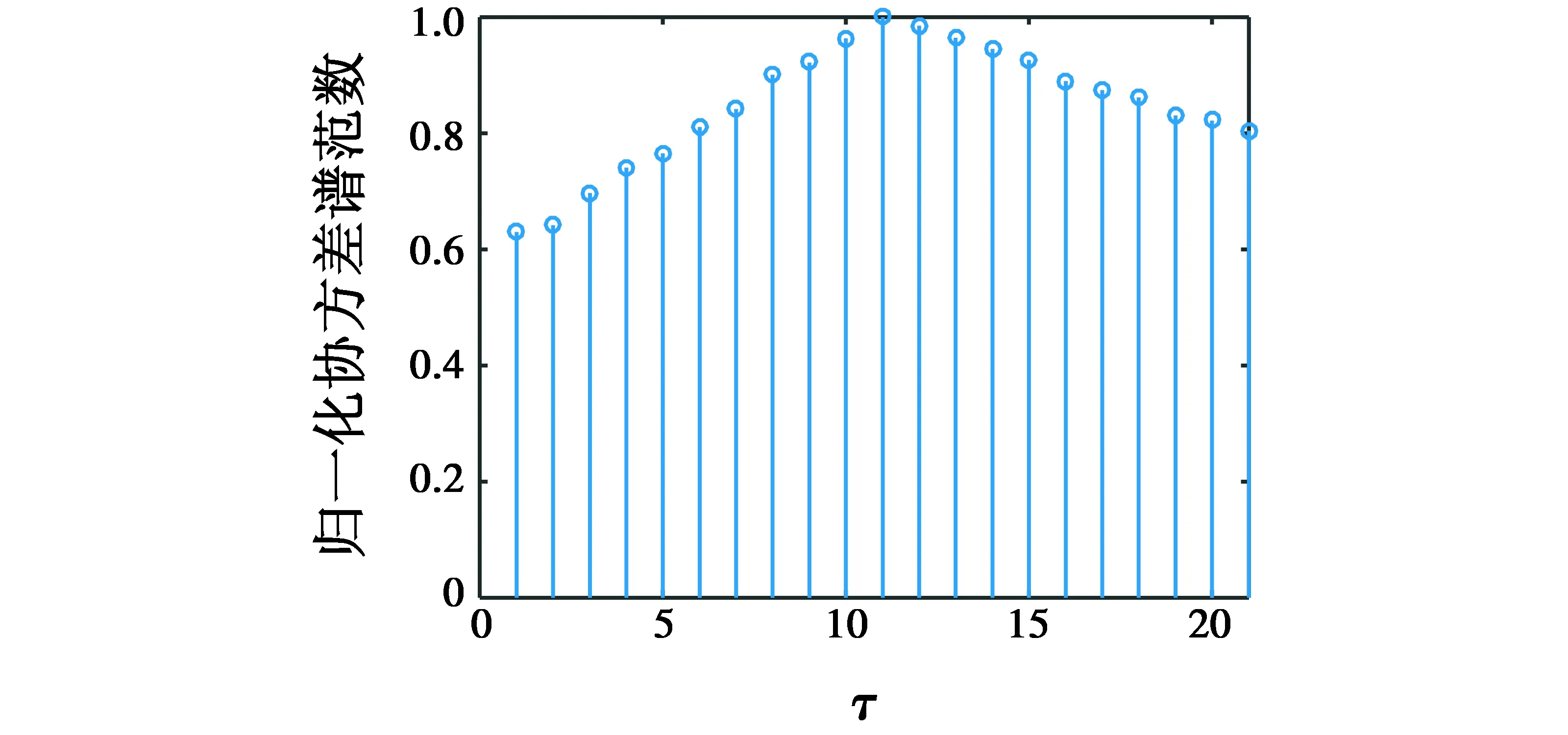
图3 延时点估计Fig.3 The delay point estimation
从图3中可以看出,当延时点为11时,信号协方差矩阵的谱范数值取得最大,说明延时11个采样点后,采样点与信息码同步,延时点在第10个采样点位置。从图3可以看出,通过计算协方差矩阵的谱范数,能够准确地估计延时点。
3.2 实验2
验证GA对周期长码直扩信号扩频码的估计效果,设置两个周期长度分别为63 bit,255 bit的扩频码,信息码长度分别为21 bit,51 bit,信息码速率分别为0.047 6 Mibit/s,0.019 6 Mibit/s,其他条件同实验1。通过GA估计的扩频码序列如图4、图5所示。
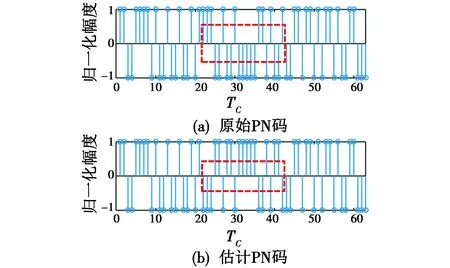
图4 63 bit PN码估计Fig.4 63 bit PN code estimation

图5 255 bit PN码估计Fig.5 255 bit PN code estimation
从图4、图5中可以看出,出现了相位模糊的情况,即其中某一段与真实的伪码相位正好相反,这是PN码估计中普遍存在的一种现象,因为观测数据是由数据码与扩频码相乘之后得来的,所以使得原先扩频码的相位变相反,针对这一问题现有的解决方法主要有三阶相关法和梅西算法等。
3.3 实验3
验证改进前后GA的迭代次数对扩频码序列估计的影响。设置两个周期长度分别为63 bit,255 bit的扩频码,信息码长度分别为21 bit,51 bit,信息码速率分别为0.047 6 Mibit/s,0.019 6 Mibit/s,其他条件同实验1,进行200次Monte-Carlo仿真,结果如图6所示。
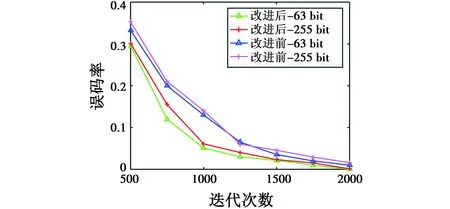
图6 迭代次数对序列估计的影响Fig.6 Influence of iteration times on bit error rate
从图6可以看出,在误码率相同时,估计周期较长的PN码需要的迭代次数一般比较多,改进后的算法减少了迭代次数从而加快了收敛速度。
3.4 实验4
验证GA与特征分解法、子空间跟踪算法和神经网络在不同的信噪比下的误码率。设置扩频码周期为255 bit,信息码长度为51 bit,信息码速率为0.019 6 MHz,迭代次数为500,其他条件同实验1,进行200次Monte-Carlo仿真,结果如图7所示。
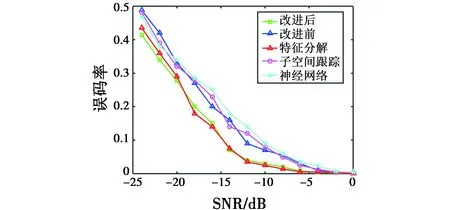
图7 不同算法的性能比较Fig.7 Performance comparison of different algorithms
从图7可以看出,随着信噪比的增加,每种算法对应的误码率在减少。改进后的GA与特征分解法在相同的信噪比下误码率保持一致,相比于其他几种算法具有较低的误码率。
3.5 实验5
验证不同频率的残留载波对扩频码序列估计的影响。设置归一化频偏分别为f1=0.002,f2=0.004,f3=0.006,f4=0.008,f5=0.01。其他条件同实验4,进行200次Monte-Carlo仿真,结果如图8所示。

图8 不同频偏对序列估计的影响Fig.8 Influence of frequency offset on bit error rate
从图8的仿真结果可以看出,在相同的SNR下,误码率随着频偏的增大而增大,说明本文所提算法在较大频偏下的估计性能不佳。
4 结论
本文提出了一种基于改进GA的周期长码直扩信号PN码的盲估计方法。利用谱范数法得到信号与PN码同步点的基础上,通过改进GA来估计PN码。仿真结果表明,利用改进的GA减少了迭代次数,并且能在较低的信噪下较好地估计出PN码序列。由于此算法在大频偏下估计性能不佳,所以需要进一步研究。
