基于预设性能的直升机火箭弹后坐力补偿控制

张逸航，王玉惠,，王 刚，刘昊天

(1.南京航空航天大学自动化学院，南京 211000；2.光电控制技术重点实验室，河南 洛阳 471000)

0 引言

武装直升机发射火箭弹武器时，火箭弹尾焰冲击发射架，导致产生后坐力。后坐力打破直升机原有的平衡状态，使得直升机的姿态发生变化。若没有及时对姿态进行有效调整，后坐力作用效果累加会严重影响射击精度，甚至威胁载机安全[1]。合理、有效地克服后坐力产生的影响，能够大幅提升直升机火箭弹射击效能。

在后坐力补偿控制方面，已经取得不少成果。夏良[2]分析了武器外挂对载机的基本参数以及稳定性的影响，并比较前飞与悬停发射对直升机产生的影响。邢君等[3]、魏衡华等[4]将后坐力视为一种扰动现象，采用PID控制，有效地抑制了射击扰动。于志等[5]在研究了后坐力对载机影响的基础上，提出基于非线性H∞方法的后坐力补偿控制方案。虽然文献[2-5]实现了武器系统和载机在后坐力的作用下仍能保持稳定，但均未涉及补偿控制时间的要求。终端滑模控制[6]、模型预测控制[7]、预设性能控制[8]等均可对系统响应时间进行约束，但终端滑模控制对超调没有限制，模型预测控制又依赖于被控对象精确的模型，相较之下，预设性能控制[9]既可实现对控制响应时间的要求，也能有效避免过高的系统超调。

预设性能控制对设计方法限制较少，因此可根据模型特点结合不同方法的优势进行设计。胡云安等[10]采用Backstepping方法对预设性能控制器进行设计，在严格反馈非线性系统中取得了理想的效果；ZHANG等[11]将预设性能控制与自适应控制结合起来，研究了舰载无人机的瞬态跟踪误差，解决了系统的跟踪控制问题；TAN等[12]针对无人机纵向模型的不确定性以及存在外部干扰的情况，提出了一种新的性能函数，并具有很好的收敛性能，设计出来的控制器具有很强的鲁棒性。上述成果充分验证了预设性能控制在解决实际问题上的优势，但由于直升机飞行特性和武器发射系统的复杂性，已有成果很难直接应用于直升机的后坐力补偿控制。

本文针对武装直升机发射火箭弹时产生的后坐力问题，基于预设性能控制方法设计了后坐力补偿控制系统。首先，给出了武装直升机姿态系统模型，并分析火箭弹发射时产生的后坐力大小和后坐力力矩对载机姿态产生的影响；然后，结合预设性能函数对姿态系统跟踪误差进行约束，采用Backstepping方法设计了预设性能控制器；最后，通过仿真验证了所设计控制器的有效性。

1 武装直升机姿态系统模型

如图1所示，通过分析计算旋翼、尾桨、平尾、垂尾和机身的受力以及重力，武装直升机的姿态动力学方程可描述为

(1)

式中：φ,θ,φ分别表示滚转角、俯仰角、偏航角；p,q,r分别表示滚转角速度、俯仰角速度和偏航角速度；Ix,Iy,Iz分别表示x,y,z平面的转动惯量；Mx,My,Mz分别表示滚转、俯仰和偏航方向的力矩。

考虑到直升机动态系统具有高耦合特性，为了便于控制，需对其中部分项进行处理。其中，由于直升机前进比μ相对较小，因此忽略其影响。当主旋翼转速恒定，且主旋翼总距控制输入保持恒定时，主旋翼拉力及扭矩力也保持恒定，在本文中，认为主旋翼总距输入保持恒定。经过处理，式(1)系统变换为

(2)

式中：x1=(φθψ)T；x2=(pqr)T；输入u=(a1 sb1 sθt r)T；

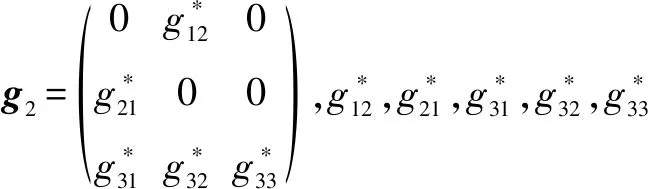
图1为直升机示意图。图1中：Ω,Ωtr分别为主旋翼和尾桨转速；Ts为旋翼拉力；FP为火箭弹后坐力。

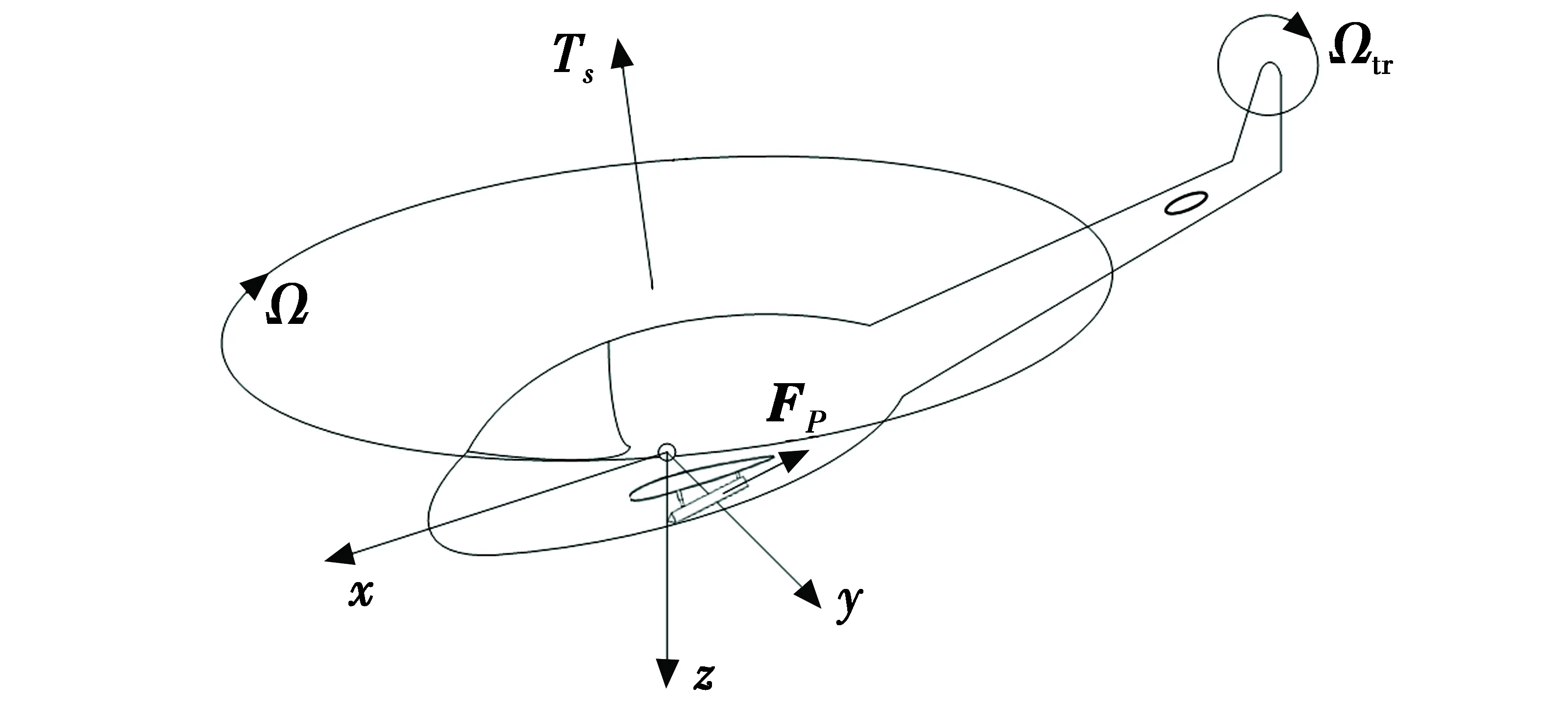
图1 直升机示意图Fig.1 Schematic diagram of a helicopter

2 火箭弹后坐力分析

武装直升机进行火箭弹发射时，内部火药燃烧产生的高温气体经由喷管形成了燃气射流[15]。当火箭弹脱离定向管时，其尾流场冲击发射架，导致发射器与载机结构间产生相互作用力，该力是后坐力的主要部分[16]。

在以往的设计中，大都将后坐力视为方向未知、大小已知的扰动，将其影响直接作用于姿态角的动态系统中。事实上，通过分析式(1)姿态系统可知，后坐力先对姿态角速度产生影响，继而影响到姿态角，因此，本文进行如下分析。

首先，火箭弹尾焰冲击发射架可以近似为轴对称射流对平板的斜冲击问题。燃气射流可以划分为近场、中场和远场，对于近场与中场，其燃气速度马赫数大于1时，燃气射流会产生正激波，因此可以采用超声速皮托管公式计算动压[17-18]，即

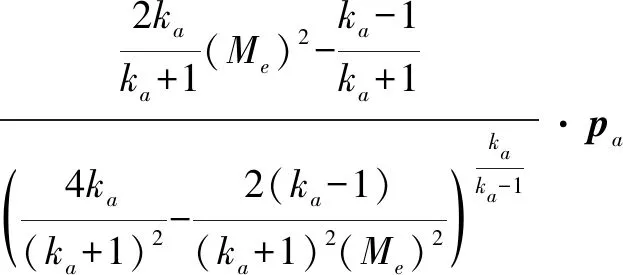
(3)

式中：pa为压缩激波前气流中的燃气静压力；ka为气流的绝热指数；Me为燃气射流马赫数。

当火箭弹逐渐飞离定向管时，定向管处燃气速度马赫数小于1，此时动压算式为

(4)

气流作用在与气流轴线成αa角的平面上的动压可以计算为

pα=kcpfsin2αa

(5)

式中，kc为气流偏斜系数，一般取0.9。

接着可以计算定向管的后坐力，定向管可以分解为多个受到同等压强的平面，总后坐力大小为所有平面的受力总和，即

(6)

式中：pj表示第j(j=1,2，…，n)个平面的压力；Δσj为压力pj作用的面积。

后坐力作用在定向管上，通过连接机构最终影响到载机姿态，图2为火箭弹发射架示意图。

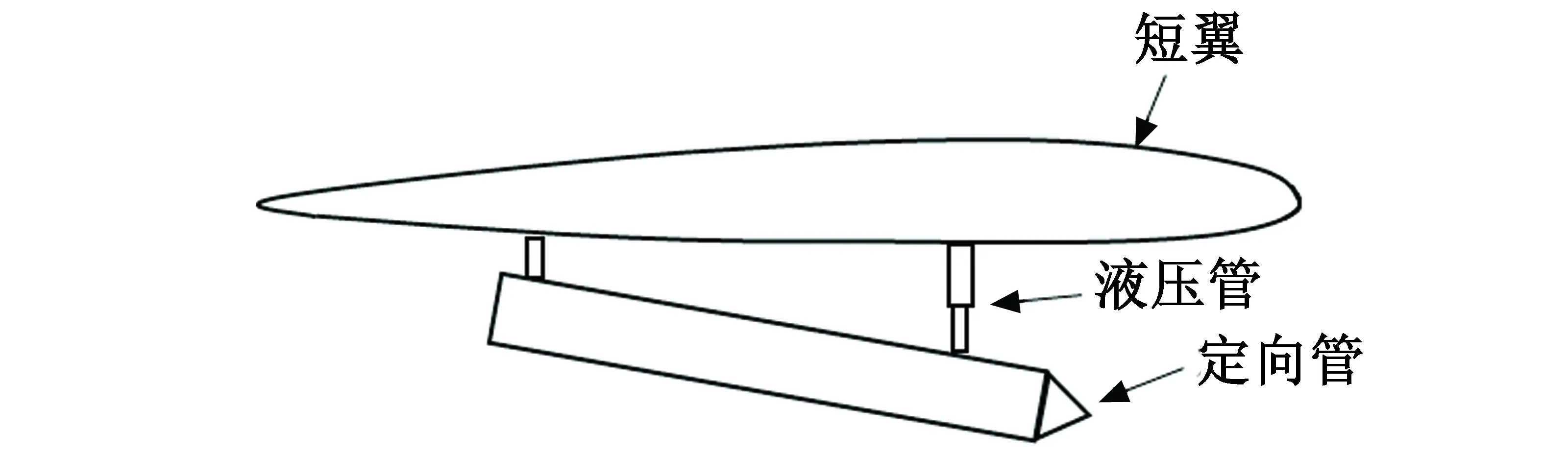
图2 火箭弹发射架示意图Fig.2 Schematic diagram of rocket launcher

当火箭弹发射时，后坐力方向沿着定向管向后，此时力平行于xoz平面，由于短翼与重心之间存在一定的高度差，进而产生影响俯仰通道的力矩。若武器为非对称发射，后坐力的产生不仅影响俯仰通道，还会对滚转与偏航通道产生影响，3个通道耦合起来对直升机扰动会十分严重。因此，在实战中，通常采用左右协同发射。

后坐力产生的力矩可以表示为

Md=FPl

(7)

式中：Md表示后坐力力矩；l表示等效力臂长度。

左右协同发射时产生的后坐力对滚转和偏航通道的影响很小，因此本文主要分析后坐力对俯仰通道的影响。在加入后坐力后，式(1)系统中俯仰通道的方程可以修改为

(8)

因此，式(2)可以写为

(9)

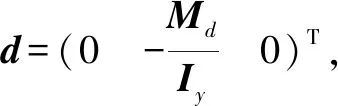
图3给出了直升机处于悬停状态时，后坐力对直升机姿态系统中俯仰角的影响。

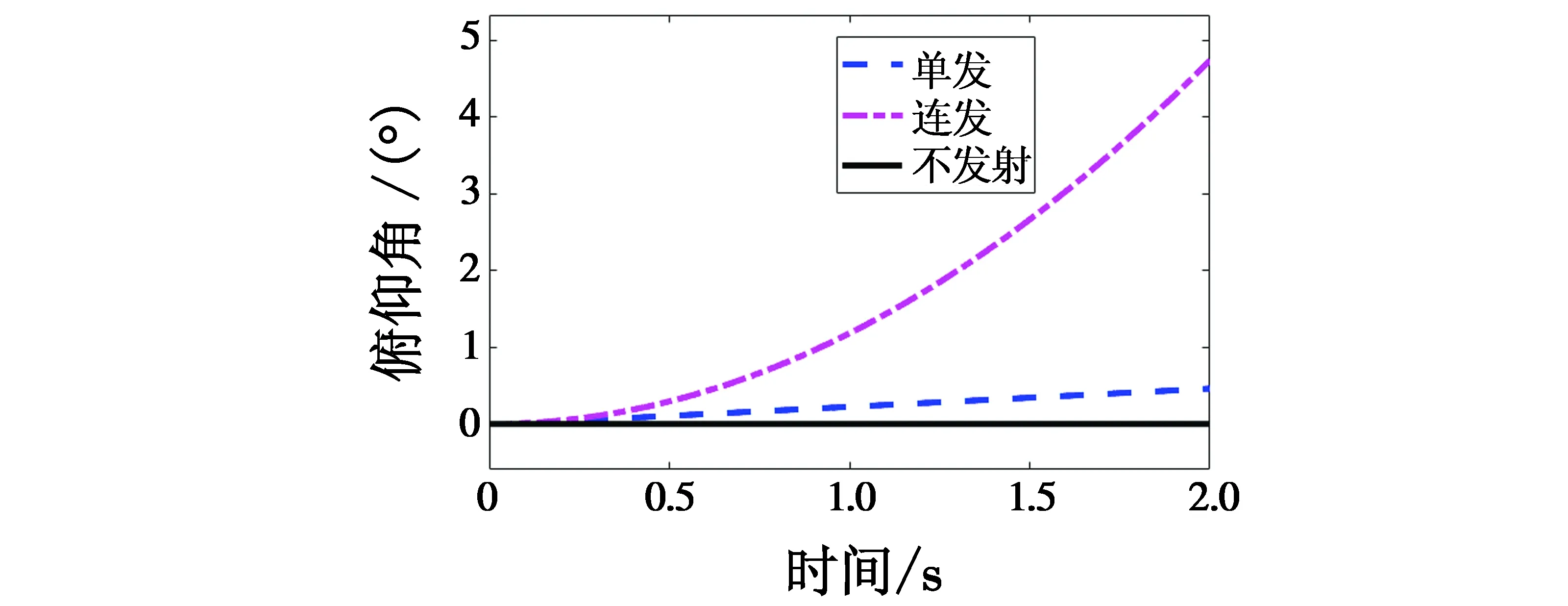
图3 后坐力对俯仰角的影响Fig.3 Influence of recoil force on pitch angle

图3中，虚线表示发射单发火箭弹造成的影响，点划线表示间隔为100 ms的连续发射。当直升机悬停射击时，发射单枚火箭弹对姿态产生的影响较小，而连续发射时产生的后坐力会导致后续的射击偏差逐渐增大。需要在发射间隔内对后坐力进行补偿控制，以保证攻击目标时打击的精确性。

3 预设性能控制器设计

预设性能控制在保证系统稳态性能的同时，还可实现系统动态性能的设计要求。具体的做法是将系统的跟踪误差限制在边界函数约束的区域内，其误差如图4所示。

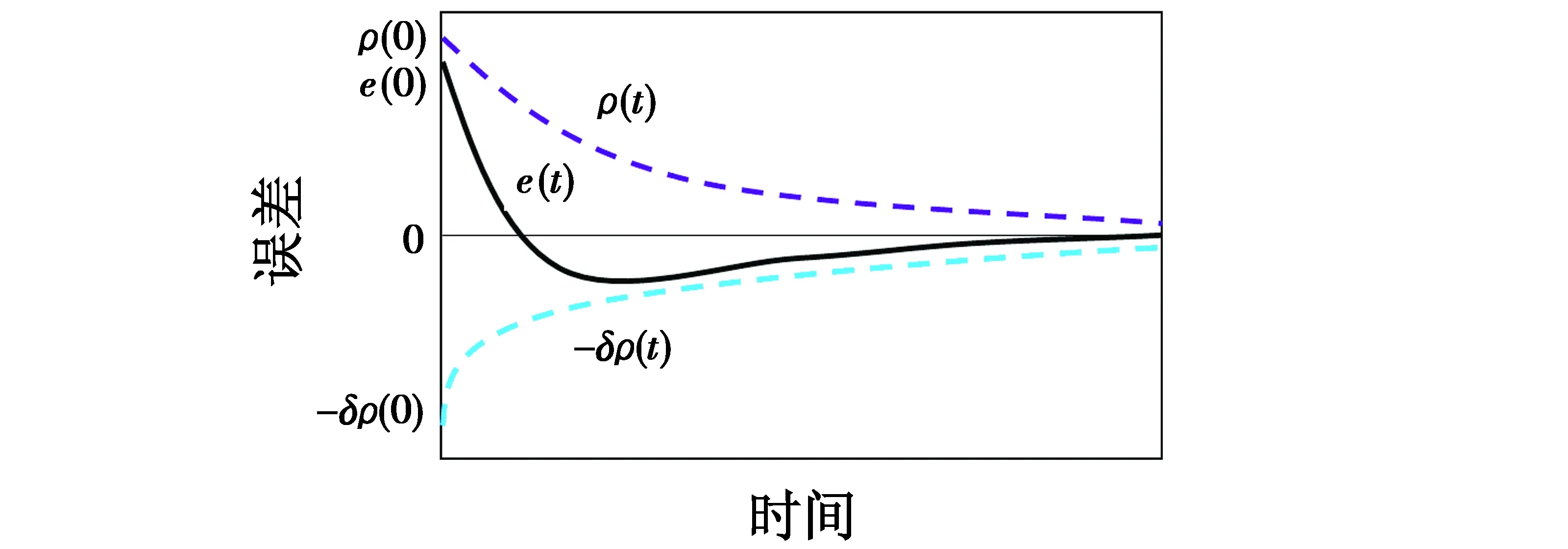
图4 跟踪误差示意图Fig.4 Schematic diagram of tracking error

当e(0)>0时，跟踪误差e(t)被限制在性能函数ρ(t)和-δρ(t)中。其中：δ∈(0,1]，为系统的响应超调量；ρ(t),-δρ(t)分别表示边界函数的上、下边界，e(0),ρ(0),-δρ(0)表示初始时刻的跟踪误差和边界。

本文中性能函数选取为

ρ(t)=ae-bt+ρ∞

(10)

式中，a,b,ρ∞>0，为预先设定的常数。

通过合理设计性能函数边界，可实现对跟踪误差动态响应的超调、调节时间以及稳态误差进行限制，从而满足后坐力补偿控制的要求，具体设计过程详见下文。

3.1 控制误差转化

在实际的控制过程中，对跟踪误差的处理比较困难，因此可以对其进行空间对等映射，从而克服性能约束函数给控制器带来的额外复杂性，实现性能约束空间到无约束空间的对等转换。

定义

e(t)=ρ(t)S(ε′)

(11)

式中：ε′为转换误差；S(ε′)为误差转换函数，是一个定义域为R、值域为[-1,1]的连续单调递增函数。

空间映射的转换函数一般采用对数型映射函数或者正切型映射函数，本文采用对数型映射函数，可表示为

(12)

根据式(11)，可以将误差转换函数S(ε′)写成

S(ε′)=e(t)/ρ(t)。

(13)

由于S(ε′)连续且单调递增，可以将误差转化函数进行逆变换得到

ε′=S-1(e(t)/ρ(t))。

(14)

对式(13)两边求导可得

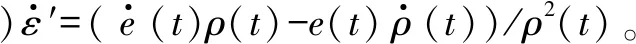
(15)

将式(11)代入式(15)，并整理可以得到

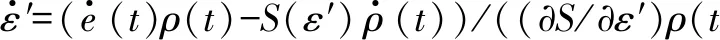
(16)

针对直升机系统，定义跟踪误差为

(17)

式中：e1表示姿态角误差；x1c表示期望姿态角；e2表示姿态角速度误差；x2c表示期望姿态角速度。

根据式(9)，建立原系统的误差模型

(18)

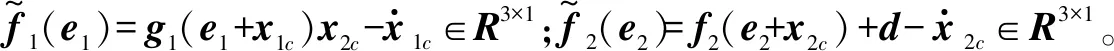
考虑到e1∈R3×1，在进行误差转化时，e1中每一个元素会对应不同的误差转换函数S(ε′)，因此针对eφ,eθ,eφ分别进行误差转化，对应的转化误差为εφ,εθ,εφ，定义ε=(εφεθεφ)T。

根据式(16)，对式(18)中第1个子系统进行误差转化，可以得到

(19)

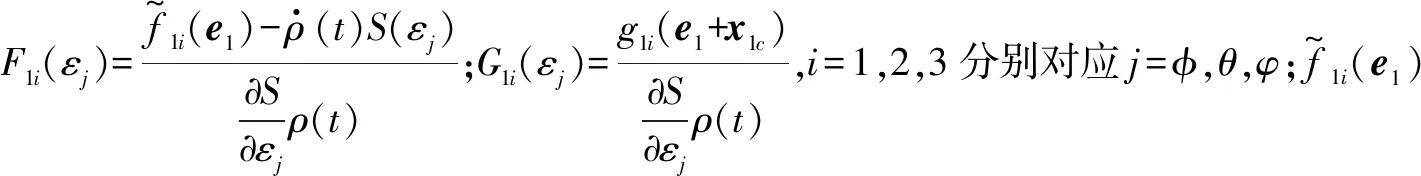
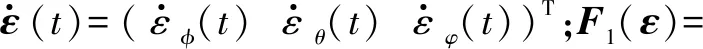
(20)

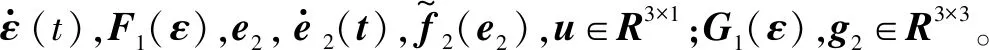
通过上述转化，可以将预设性能函数与直升机动态方程结合起来。

3.2 控制器设计

控制器采用Backstepping方法进行设计。

则对式(20)中第1个子系统进行转化得

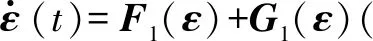
(21)

设计虚拟控制律α1为

(22)

式中，k1为设计参数，其值为正。

则有

(23)

选取Lyapunov函数

V1=0.5εTε

(24)

对其求导得

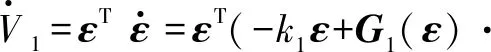
(25)

对式(20)中第2个子系统进行转化得

(26)

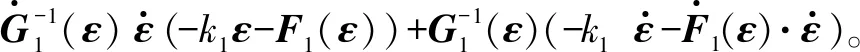
设计实际控制律为

(27)

式中，k2为设计参数，其值为正。

则式(26)可以写为

(28)

选取Lyapunov函数

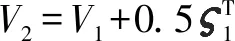
(29)

对其求导得

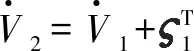
(30)

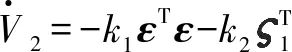
(31)

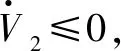
4 仿真结果分析

为了验证本文所设计预设性能控制器的有效性，取设计参数k1=1，k2=1。

取ρ∞=0.01，即稳定状态时直升机姿态变化不超过0.01°，考虑到发射间隔td=100 ms，根据式(10),取a=0.5，b=40。则采用的预设性能函数为ρ=0.5e-40t+0.01，δ=0.5。

设载机发射火箭弹时处于水平悬停状态，定向管与发射架夹角αa=10°。在发射过程中，载机的滚转角与偏航角受到的影响较小，因此本文主要分析俯仰角产生的变化。图5给出了俯仰角随时间变化的仿真图像，可以看出在0.1 s时，第2发火箭弹发射，直升机俯仰角误差变化在0.01°左右，后续发射的火箭弹也能保证其攻击精度。

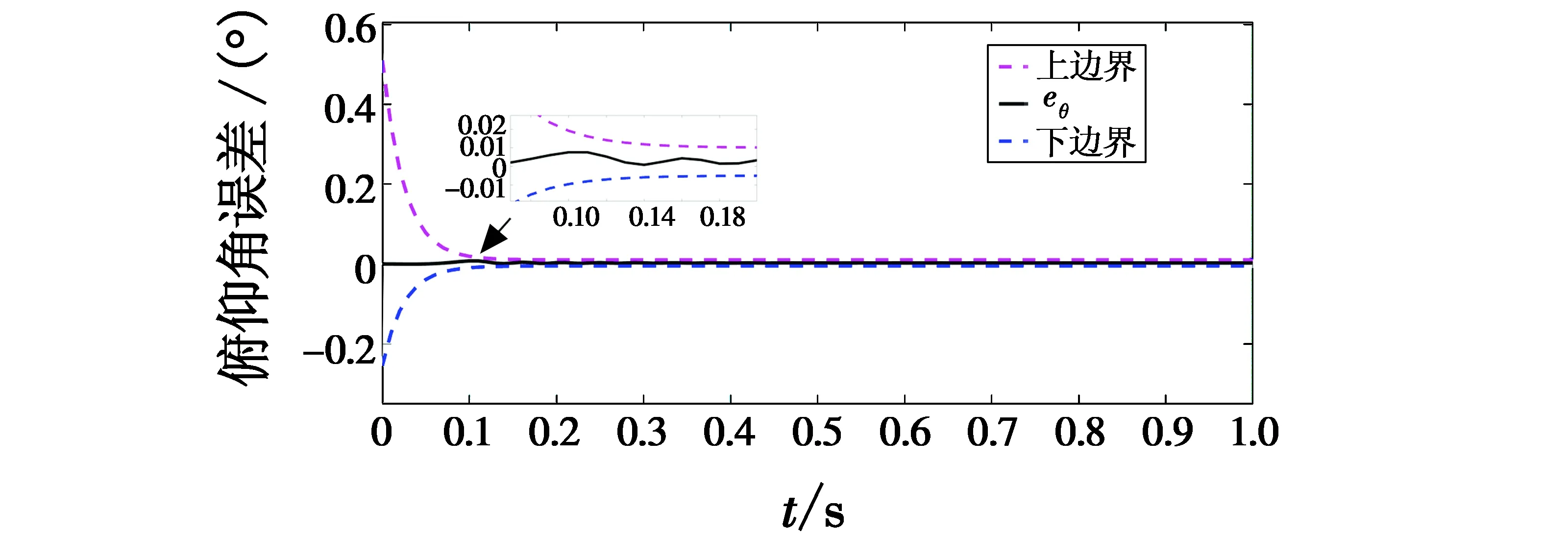
图5 俯仰角跟踪误差曲线Fig.5 Tracking error curve of pitch angle

图6和图7分别给出了在后坐力的作用下，采用补偿控制器前后，直升机的俯仰角速度和俯仰角的对比曲线。可以看出，未引入控制器时，俯仰角速度受后坐力影响快速增加，从而导致俯仰角迅速增大，载机姿态不再稳定。采用预设性能控制器后，俯仰角稳定性大幅增加，补偿效果明显。

图6 俯仰角速度补偿前后对比图Fig.6 Comparison of pitch angular rates before and after compensation

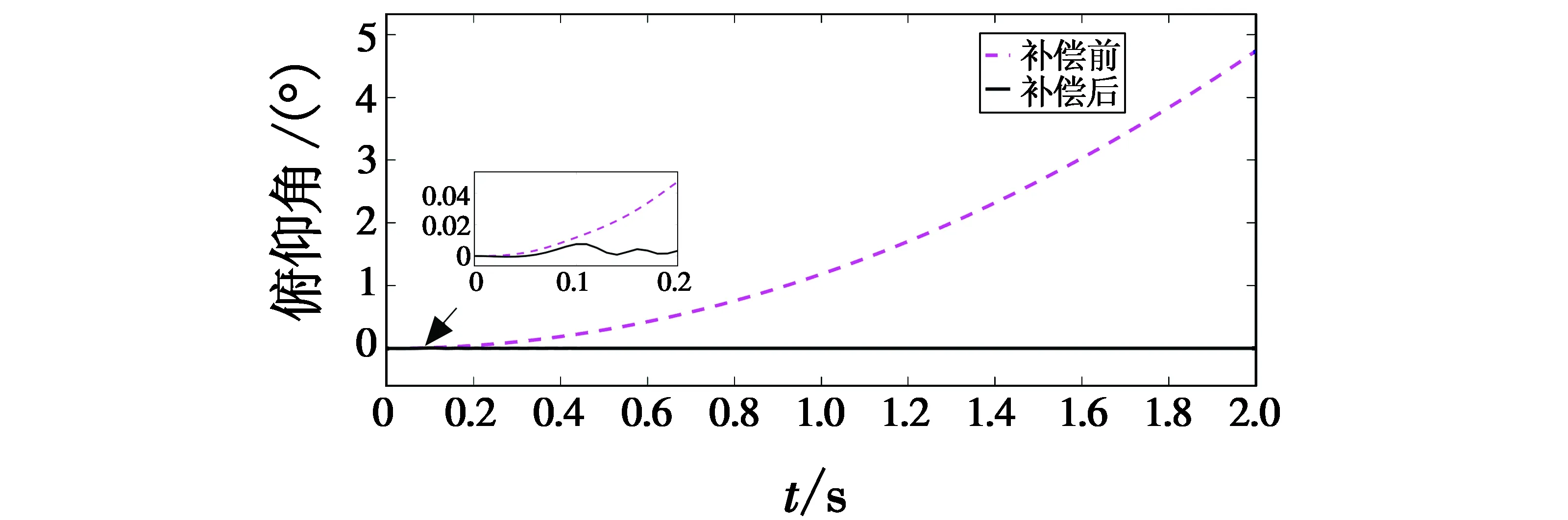
图7 俯仰角补偿前后对比图Fig.7 Comparison of pitch angle before and after compensation

图8分别给出了采用预设性能函数、不采用预设性能函数与滑模控制3种方法的对比。当不采用预设性能函数设计控制器时，虽然最终可以收敛，但是调节时间过长。滑模控制也可以达到控制目标，但会带来抖振，在本系统中，预设性能控制效果更好。

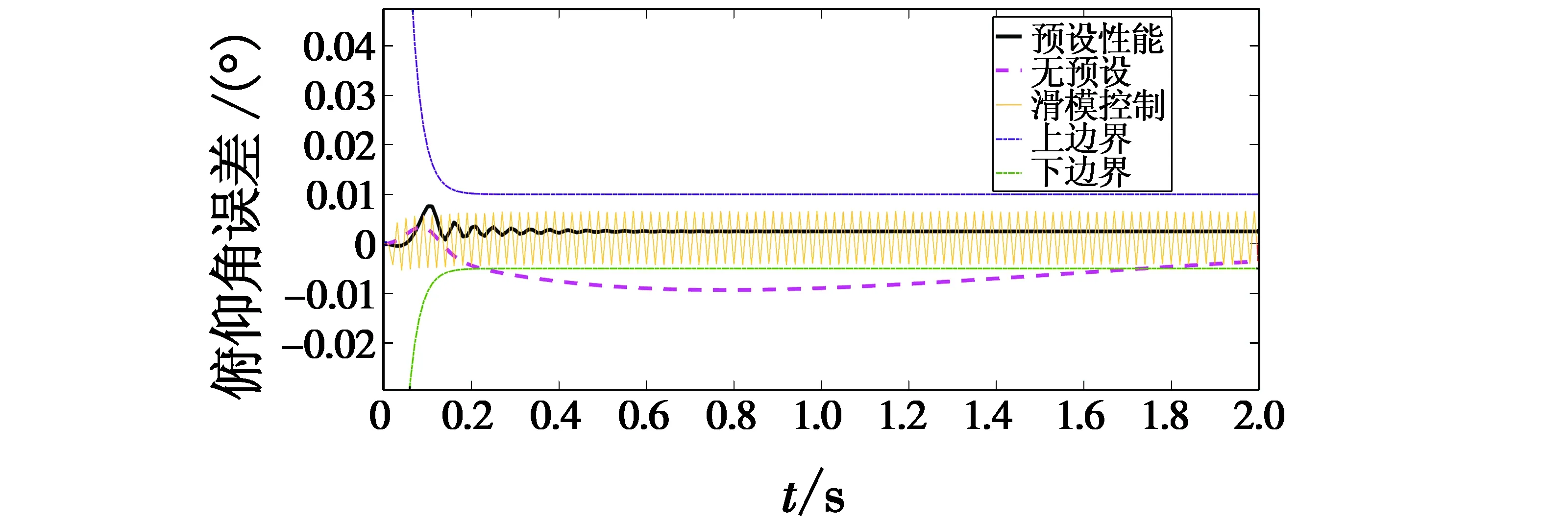
图8 不同控制方法对比图Fig.8 Comparison of different control methods

5 结论

本文针对武装直升机进行火箭弹发射时产生的后坐力问题进行分析，根据火箭弹发射的实际情况估算出火箭弹后坐力大小。结合发射角度和发射方式对力矩进行计算，进而分析后坐力对载机姿态产生的影响。针对产生的影响，本文提出基于预设性能的后坐力补偿控制方案，解决了连续发射火箭弹导致的直升机姿态不稳定和射击误差逐渐增大的问题，仿真验证了所设计方案的有效性。本文的研究为提高武装直升机连射火箭弹的打击精确性提供了重要参考。