基于2D-RFRFT的密集假目标干扰自适应抑制算法

张 亮，张翔宇，杨大伟，王培源，于海涛

(1.海军航空大学，山东 烟台 264000；2.中国人民解放军94326部队，济南 250000；3.中国人民解放军94201部队，济南 250000)

0 引言

现代雷达多采用全相参体制[1]，而基于数字射频存储装置(Digital Radio Frequency Memory,DRFM)的密集假目标干扰(Dense False-target Jamming,DFJ)是对抗相参雷达典型干扰样式[2]。根据雷达接收干扰信号相参性，DFJ可细分为相参DFJ[3-4]和非相参DFJ[5-8]。相参DFJ追求制造高逼真虚假目标，具体实施中要求干扰方准确测量雷达脉冲重复频率(Pulse Repetition Frequency,PRF)，当雷达PRF存在抖动或捷变解模糊时[9]，干扰方利用直方图、PRI变换等手段预测下一个脉冲出现时间基本不可能[10]；非相参DFJ无需雷达PRF先验信息，依靠干扰数量和功率上的绝对优势，破坏雷达动目标检测(Moving Target Detection,MTD)功能，降低真实目标检测概率。为对抗自卫式非相参DFJ(简称DFJ)，文献[5]针对匀速目标脉压后峰值慢时间直线特征，通过Hough正反变换重构真实目标；文献[6-7]将该思想进一步拓展至捷变频雷达。上述算法在具体实现上要求对脉压后回波数据二值化处理，即尽可能将噪声数据置0、真实回波和干扰数据置1，由于缺乏旁瓣抑制环节，当干扰功率较高时，限幅后的干扰旁瓣同样会影响真实目标检测。文献[8]验证了多参数联合捷变抑制DFJ良好效果，多参数联合捷变是雷达系统抗干扰设计的重要趋势，工程上需解决参数捷变与雷达体制兼容性难题，而文献中未给出有效解决方案。另外，自卫式干扰机通常存在瞬时机动，雷达MTD处理下目标存在多普勒展宽，文献[5-8]均未考虑该情况。

针对上述问题，本文以线性调频(Linear Frequency Modulation,LFM)相参雷达抗自卫式DFJ为背景，提出基于二维精简分数阶傅里叶变换(Two-Dimensional Reduced Fractional Fourier Transform,2D-RFRFT)的密集假目标干扰自适应抑制算法。首先，对经典分数阶傅里叶变换(Fractional Fourier Transform,FRFT)进行简化，设计2D-RFRFT；其次，根据发射信号调频斜率确定快时间变换阶次pk，计算回波(pk,0)阶的2D-RFRFT，利用中位数绝对偏差识别剔除各u域单元上的干扰离群点；然后，估计目标加速度确定慢时间变换阶次pa，计算干扰剔除后回波(pk,pa)阶2D-RFRFT；最后，峰值搜索得到目标对应坐标，根据坐标位置确定目标距离和径向速度。

1 干扰特性分析

窄带条件下，设自卫式干扰机为点目标，初始距离Rt，径向速度vt，径向加速度at，雷达在干扰机方位接收真实回波基带信号为

(1)

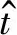
(2)

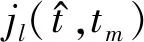
(3)

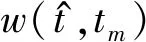
(4)

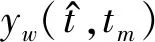
2 精简分数阶傅里叶变换

由式(1)可知，真实回波快、慢时间均为LFM信号，快时间调频斜率(发射信号调频斜率)已知，慢时间调频斜率(与目标加速度有关)未知，理论上利用二维信号处理工具对1个CPI回波整体处理，可达到常规脉冲压缩、相参积累相同效果[11-12]。常用LFM信号处理工具包括FRFT[13]、线性正则变换[14]、Chirp傅里叶变换[15]、双正交傅里叶变换[16]等，其中以FRFT研究最为广泛。基于量纲归一化Ozaktas采样型离散FRFT(Discrete Fractional Fourier Transform,DFRFT)，以其计算复杂度与快速傅里叶变换相当、较好逼近连续FRFT、适于较大调频斜率LFM信号检测等优点[17]，在FRFT数值计算中应用广泛，由于涉及1个CPI回波，对DFRFT做简化处理可更好满足本文需求。当旋转角度α≠nπ(n∈Z)，信号x(t)连续FRFT定义为[12]

(5)

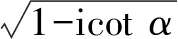
(6)

式中：h(u)=exp(-iπu2tan(α/2));g(u)=exp(iπ·(cscα)·u2);⊗为卷积符号。假设x(u)为雷达发射信号，根据调频斜率可确定变换阶次pk=arccot[-k/(π/2)]，令p=pk代入式(6)，得到

[x(u)h(u)]⊗[g(u)]=[rect(u/Tp)e-iπ(csc αk)·u2]◇
[e-iπ(csc αk)·u2]

(7)

式中：αk=pkπ/2为雷达发射信号调频斜率对应旋转角度；◇为互相关符号。式(7)可理解为以g*(u)为匹配信号(*为共轭符号)，对x(u)h(u)进行“脉冲压缩”，由于g*(u)支撑域大于x(u)h(u)，且两者调频斜率相同，“脉压”输出辛格函数，因此从目标检测角度将式(6)前两项省略，得到其约值，可表示为

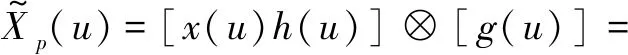
(8)

本文称式(8)为信号x(t)的精简分数阶傅里叶变换(Reduced Fractional Fourier Transform,RFRFT)，RFRFT与FRFT关系为

(9)

式(8)拓展至二维，得到信号x(s,t)的(p1,p2)阶2D-RFRFT[14]为

(10)

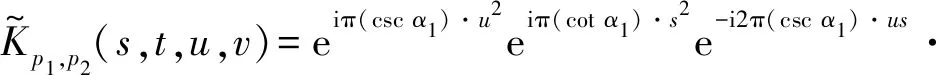
(11)

3 干扰抑制原理

3.1 真实回波与干扰2D-RFRFT

为分析真实回波、DFJ信号2D-RFRFT分布差异，设阶次p1=pk，p2=0，将式(3)代入式(10)得到回波(pk,0)阶2D-RFRFT为

(12)

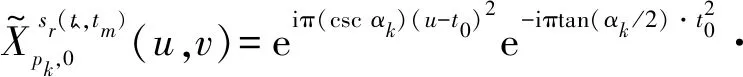
(13)

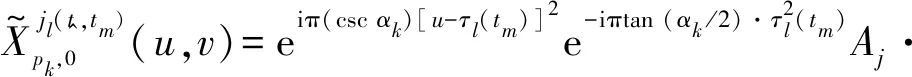
(14)

3.2 基于离群点检测的干扰剔除方法

离群点检测是数据挖掘理论主要任务之一，常用检测准则包括“3σ”准则、四分位间距准则、格拉布斯准则、狄克逊准则、肖维勒准则等，上述准则均假设样本总体服从正态分布，对于非正态分布总体，需设计对应检测方法[21]。雷达所处环境复杂，受地海杂波、目标起伏、干信比(Jamming to Signal Ratio,JSR)等因素影响，要确定回波2D-RFRFT分布类型非常困难。中位数绝对偏差(Median Absolute Deviation,MAD[22])是一种稳健的单变量离差统计测量，崩点为0.5，即允许集合中离群点最大占比为50%，且不要求足够多的样本(雷达相参积累个数有限)，相比方差、标准差受离群点影响较小，对于没有均值和方差的对称分布类型同样适用。设回波2D-RFRFT的1个u域单元信号为样本集X，其MAD算式为

MMAD=b·med[|xi-med(X)|]

(15)

式中：med(·)表示求中位数;b=1/Q(0.75)，为校正因子，Q(0.75)为75%分位数;xi为样本。当样本服从正态分布时，b取1.482 6。与“3σ”准则相似，根据样本值与中位数的距离，确定离群点鉴别准则为

|xi-med(X)|/MMAD>tth

(16)

式中，tth为鉴别门限，可取3(非常保守)，2.5(一般保守)，2(不保守)。需要注意的是，对于回波2D-RFRFT，X中样本值为复数，可区分实部、虚部分别进行离群点检测，得到两组标签，再进行“或”运算得到最终检测标签，根据最终检测标签将回波2D-RFRFT中I，Q数据置零，完成干扰剔除。

3.3 干扰剔除后真实目标检测方法

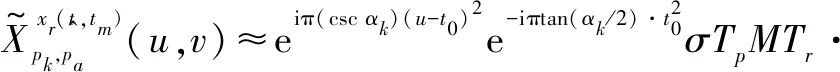
(17)

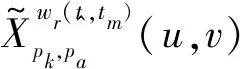
Rt=cu0/(2cosαk)

(18)

vt=λv0/(2sinαa)

(19)

at=-λcot(αa/2)。

(20)

估计目标加速度最直接的方法是设计步长进行阶次搜索，为减少搜索次数，可行的方法包括拟牛顿迭代法、分数阶相关法、高阶矩法等[12]，在此不做详述。综上所述，图1给出了所提算法干扰抑制流程。

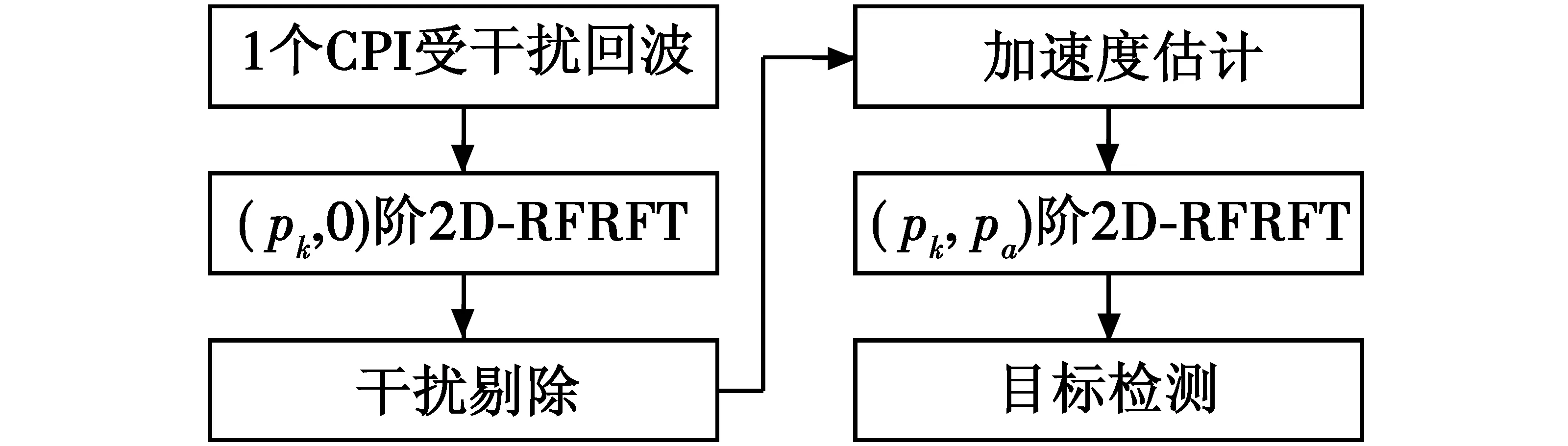
图1 干扰抑制流程Fig.1 Jamming suppression process

4 仿真结果与分析

4.1 参数设置

设雷达载频为400 MHz，重频为2000 Hz，相参积累个数为128，雷达发射LFM脉冲信号，脉宽为50 μs，带宽为4 MHz，采样频率为16 MHz；自卫式干扰机初始距离为31 km，径向速度为120 m/s，径向加速度为600 m/s2，每个重复周期内释放5个干扰信号，共计释放640个干扰信号；为有效覆盖真实目标，设定脉压后假目标在距离27～42 km范围内随机分布。

4.2 算法可行性仿真分析

设脉压前回波SNR为-15 dB、JSR为25 dB，根据雷达发射信号调频斜率确定快时间变换阶次pk，受干扰回波(pk,0)阶2D-RFRFT如图2所示。干扰离群点“凌乱”分布于第1400～2500个u域单元内，由于干扰功率过大，图2中无法看到真实目标所处u域单元。

图2 回波(pk,0)阶2D-RFRFT结果Fig.2 Echo(pk,0) order 2D-RFRFT result

设鉴别门限为2.5，利用3.2节方法对回波(pk,0)阶2D-RFRFT实、虚部分别进行离群点检测，“或”运算得到最终检测标签如图3所示，干扰离群点被有效检测，同时检测出部分噪声。为显示检测细节，取图3中第1800～2100个u域单元，结果如图4所示，干扰离群点主瓣及部分旁瓣均被有效检测。

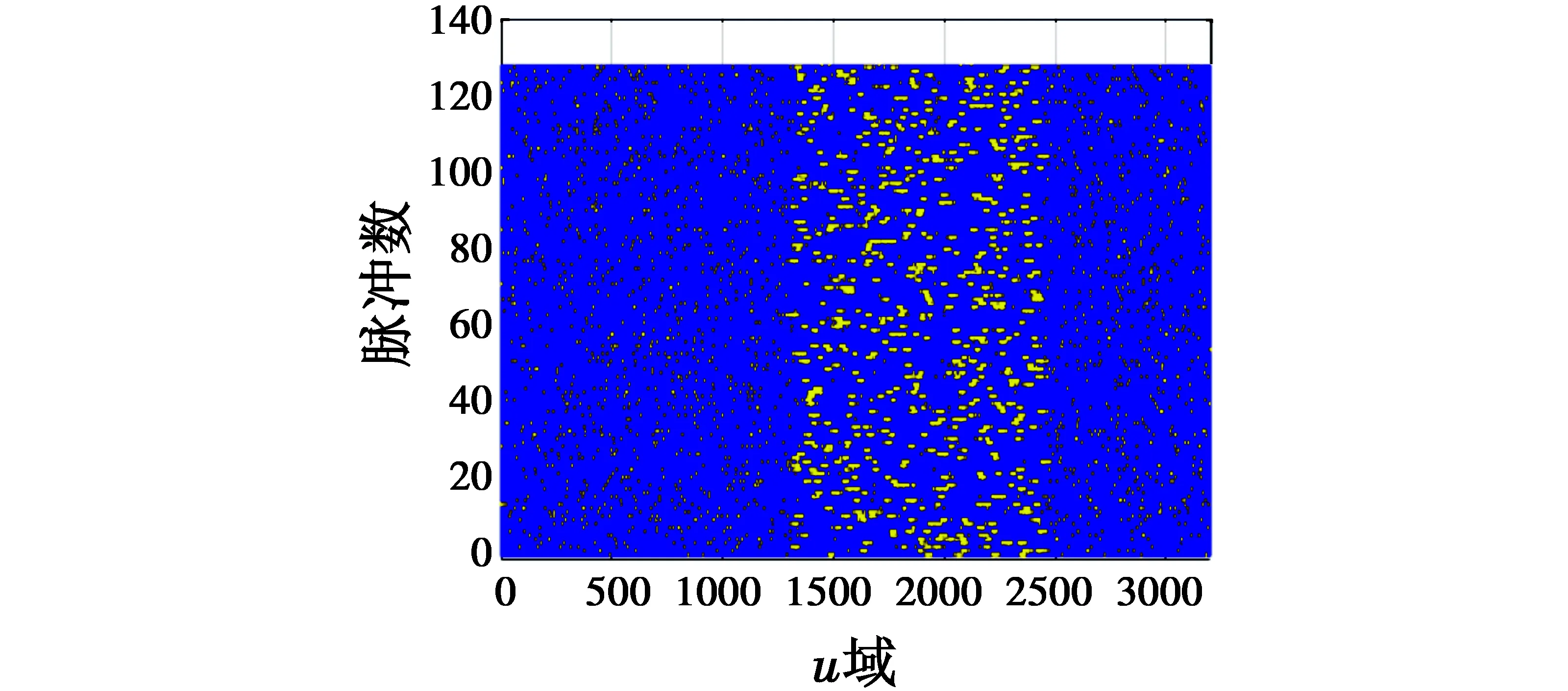
图3 离群点最终检测标签Fig.3 The final detection labels of outliers

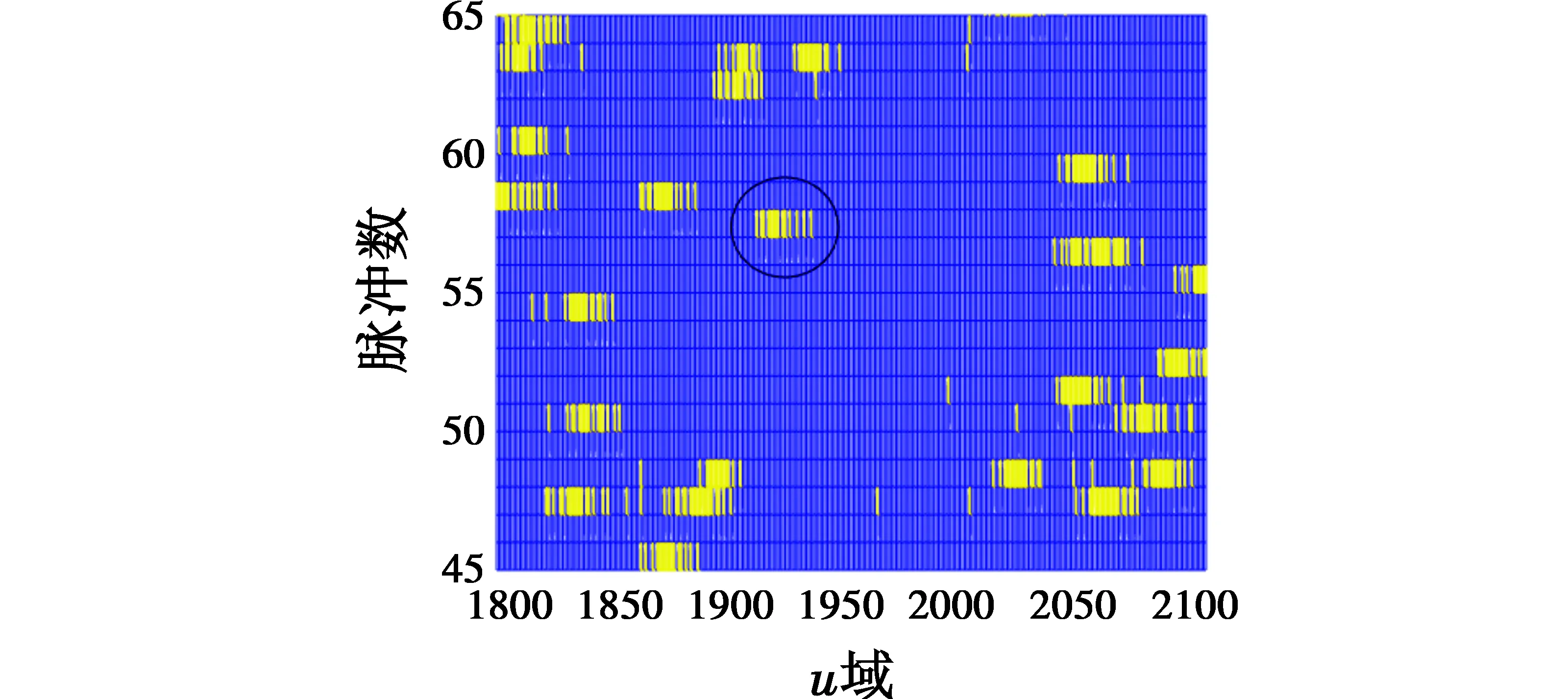
图4 离群点检测细节Fig.4 Outlier detection details

根据最终检测标签，将回波2D-RFRFT中I，Q数据同时置零，结果如图5所示。对比图2可知，干扰被有效剔除，图5中可看到目标所处u域单元。

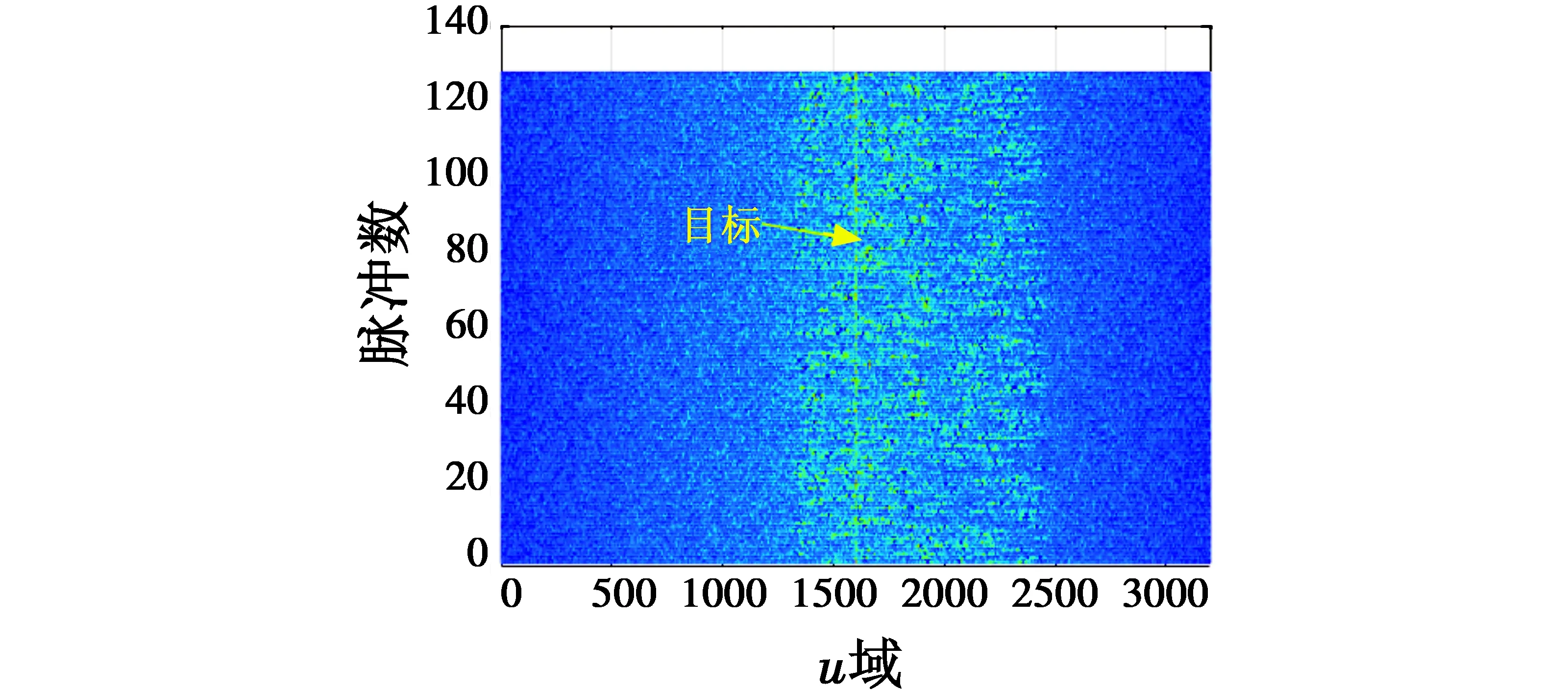
图5 干扰剔除效果Fig.5 Jamming elimination effect

计算干扰剔除后回波(pk,1)阶2D-RFRFT，结果如图6所示，能够检测到目标，但目标存在一定展宽。取图6第1601个u域单元信号，设定阶次步长为0.02，搜索范围0～2，最大高阶矩准则估计目标加速度[12]，最大矩值对应阶次为1.04，估计得到目标加速度为743.1 m/s2，与仿真使用600 m/s2较为接近。根据目标加速度确定阶次pa，计算干扰剔除后回波(pk,pa)阶2D-RFRFT，图7对比抑制前回波相参积累结果，给出了所提算法干扰抑制效果图。抑制前，真实目标被干扰信号淹没，抑制后，能够检测到真实目标，且多普勒扩展问题被有效解决，根据目标峰值坐标得到目标初始距离为31 km，径向速度为120.6 m/s，与仿真使用的31 km，120 m/s基本一致。

图6 干扰剔除后回波(pk,1)阶2D-RFRFTFig.6 Echo(pk,1) order 2D-RFRFT result after jamming elimination

图7 干扰抑制效果Fig.7 Jamming suppression effect

4.3 算法效能仿真分析

目标瞬时机动会导致多普勒展宽，低SNR条件下影响真实目标检测，雷达遭受DFJ干扰后检测性能会进一步恶化，以真实目标检测率(Real Target Detected Ratio,RTDR)为指标评估算法效能。首先，分析干扰机瞬时机动和DFJ对目标检测影响。SNR取值-20～0 dB，间隔1 dB，利用单元平均恒虚警检测器对MTD处理后的回波进行目标检测，运行蒙特卡罗仿真500次(下同)，图8(a)给出了雷达未受干扰时RTDR随SNR变化曲线。低SNR条件下，目标瞬时机动对目标检测影响较大，加速度越大，RTDR越小。SNR分别取值-20 dB，-15 dB，-10 dB，-5 dB，JSR取值0～60 dB，间隔5 dB，干扰机加速度为600 m/s2，雷达遭受干扰后，RTDR随JSR变化曲线如图8(b)所示。高JSR条件下，DFJ对真实目标检测影响更为明显，当JSR大于25 dB时，不同SNR条件下RTDR均接近于0，干扰信号淹没真实目标。

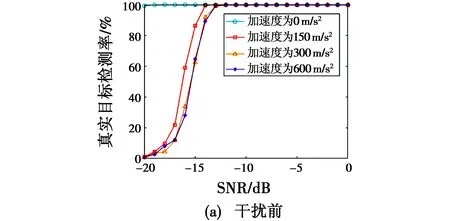
图8 雷达遭受干扰前后真实目标检测概率Fig.8 RTDR before and after radar is jammed

其次，分析所提算法的干扰抑制效能。SNR，JSR与干扰机加速度取值同上，区分4种离群点检测准则，即“3σ”准则、1.5倍四分位间距准则、格拉布斯准则和2.5倍MAD准则，图9给出了干扰抑制后RTDR随JSR变化曲线。对比图8可知，不同准则下所提算法干扰抑制后，RTDR为零的临界JSR相比抑制前均有显著提升，总体上看，1.5倍四分位间距准则、格拉布斯准则、2.5倍MAD准则对干扰离群点的检测效果较好，干扰抑制后RTDR为零的临界JSR相比抑制前提升约25 dB，“3σ”准则检测效果相对较差，RTDR为零的临界JSR相比抑制前提升约20 dB。

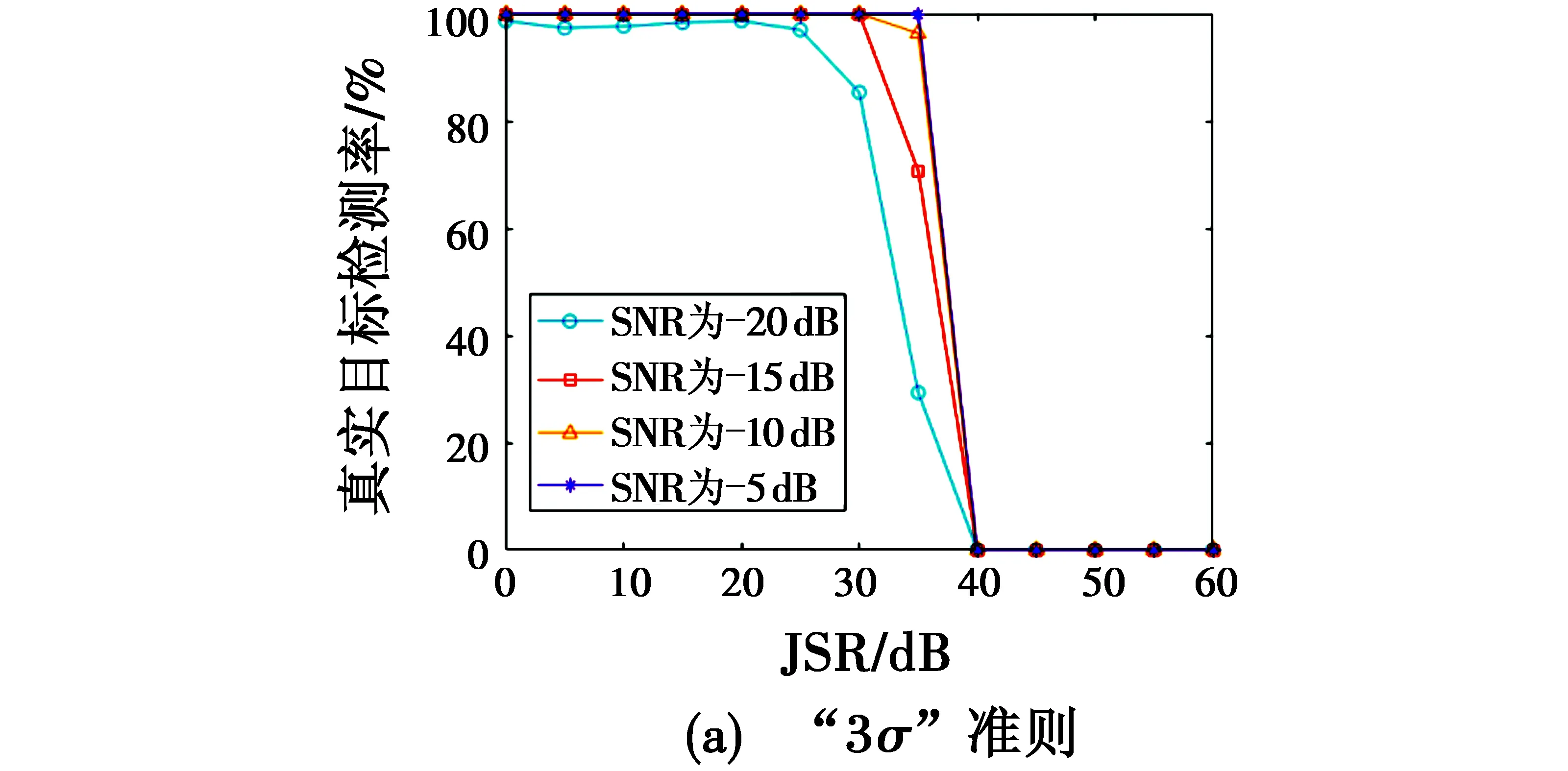
图9 干扰抑制后RTDR随JSR变化曲线Fig.9 Change of RTDR with JSR after jamming suppression

最后，分析假目标数量对算法效能的影响。SNR分别取值-15 dB，-10 dB，-5 dB，JSR取值35 dB，1个重复周期内假目标数量为5～19个，间隔2个，基于2.5倍MAD准则检测干扰离群点，图10给出了RTDR随假目标数量变化曲线。RTDR与假目标数量近似呈反比关系，即SNR越低，假目标数量越多，RTDR越小，分析原因是假目标数量越多，剔除后的剩余干扰也越多，同时由于干扰信号与真实回波重叠概率增大，干扰剔除对真实回波的破坏也相应增大。

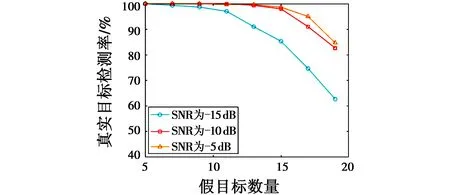
图10 干扰抑制后RTDR随假目标数量变化曲线Fig.10 Change of RTDR with false targetnumber after jamming suppression

5 结束语

为对抗自卫式密集假目标干扰，提出基于2D-RFRFT的密集假目标干扰自适应抑制算法。仿真结果表明：高JSR条件下的密集假目标干扰和目标瞬时机动会使相参雷达失去积累优势，通过补偿目标多普勒频率、剔除干扰主副瓣能量，可显著提升目标检测概率；算法对干信比具备较强容忍度，干扰抑制后真实目标检测率为零的临界JSR相比抑制前提升约20～25 dB；高斯白噪声背景下，1.5倍四分位间距准则、格拉布斯准则、2.5倍MAD准则干扰离群点检测效能相差不大，且均优于“3σ”准则。需要注意的是，本文设计运用2D-RFRFT和2D-CFRFT是为了解决目标瞬时机动条件下的多普勒展宽问题，非干扰抑制必备环节。对于匀速目标，仅需对脉压后回波沿慢时间进行离群点检测和干扰剔除。同理，对于窄脉冲干扰，可在脉压前对回波沿慢时间进行离群点检测和干扰剔除，抑制思想相同，限于篇幅，不做详述。