“低慢小”目标多体制武器分配优化模型
2022-03-17苑文楠贾彦翔邱旭阳
苑文楠,贾彦翔,吕 鑫,侯 师,邱旭阳
(北京机械设备研究所,北京 100000)
0 引言
“低慢小”(Low Slow Small,LSS)目标主要是在低空慢速飞行的小型无人机或空浮器,具有侦测难、管制难、治理难等特点[1]。相比于先进的大型军用无人机,利用“低慢小”进行骚扰破坏更易让犯罪分子有可乘之机,对国家和民众安全、社会秩序会造成严重威胁[2]。近年来,针对“低慢小”目标传统火力拦截手段中遇到的问题[3],国内外多家军工企业研制了激光、无线电和柔性网等新型拦截装备。其中,激光武器是通过辐照使目标材料或状态受到损伤以实现拦截目的[4],但该武器不具备全天候作战能力,且受天气干扰较大,存在跟踪瞄准难度较高、能量转换效率低[5]的问题;无线电武器通过发射无线电波束干扰无人机的控制信号和GPS导航信号,但这种作战机理导致其拦截目标类型比较单一,且易影响正常的民生活动[6];柔性网式软杀伤拦截武器可实现对目标的高精准拦截,但作战距离仅有400~500 m,且作战效能受环境影响较大。由此可以看出,单一体制的拦截手段很难满足对“低慢小”目标的防控要求。
另一方面,虽然国内外学者在武器目标火力打击决策方面进行了大量模型建立和算法求解的研究[7-10],但研究主要致力于解决某特定问题,而在“低慢小”目标场景的应用较少。首先,本文开展集成激光、无线电及柔性网等多手段协同防御的多体制复合拦截技术,以提高目标的拦截概率和装备的作战效能;然后,改进传统武器分配模型,讨论3种拦截武器在4个不同维度上的约束条件,引入武器拦截权重因子,建立以目标毁伤价值最大为优化目标的数学模型,并采用遗传算法进行求解;最后,构建仿真算例验证所建模型的执行效率及计算结果的有效性。
1 模型的建立
1.1 传统武器目标分配模型
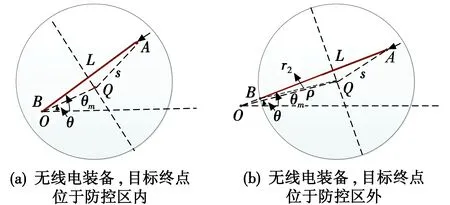
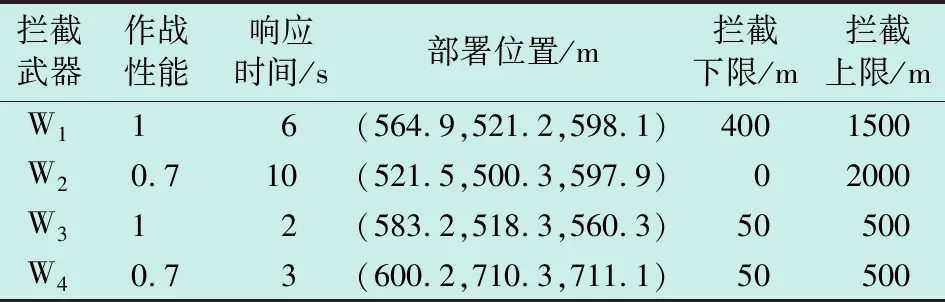
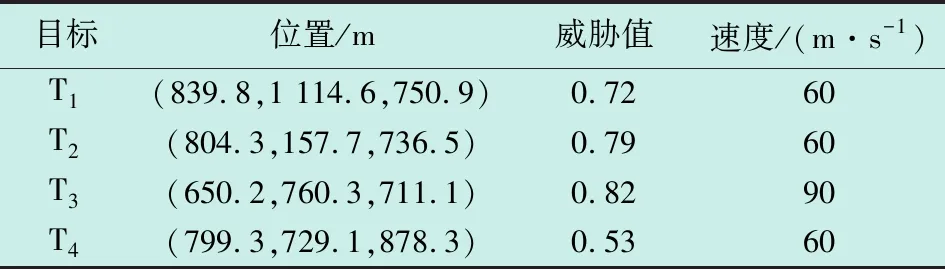
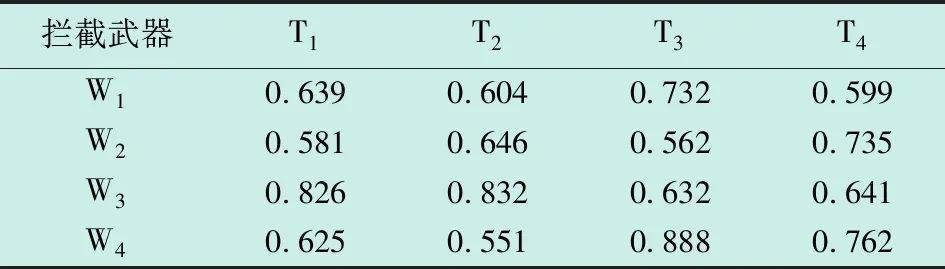
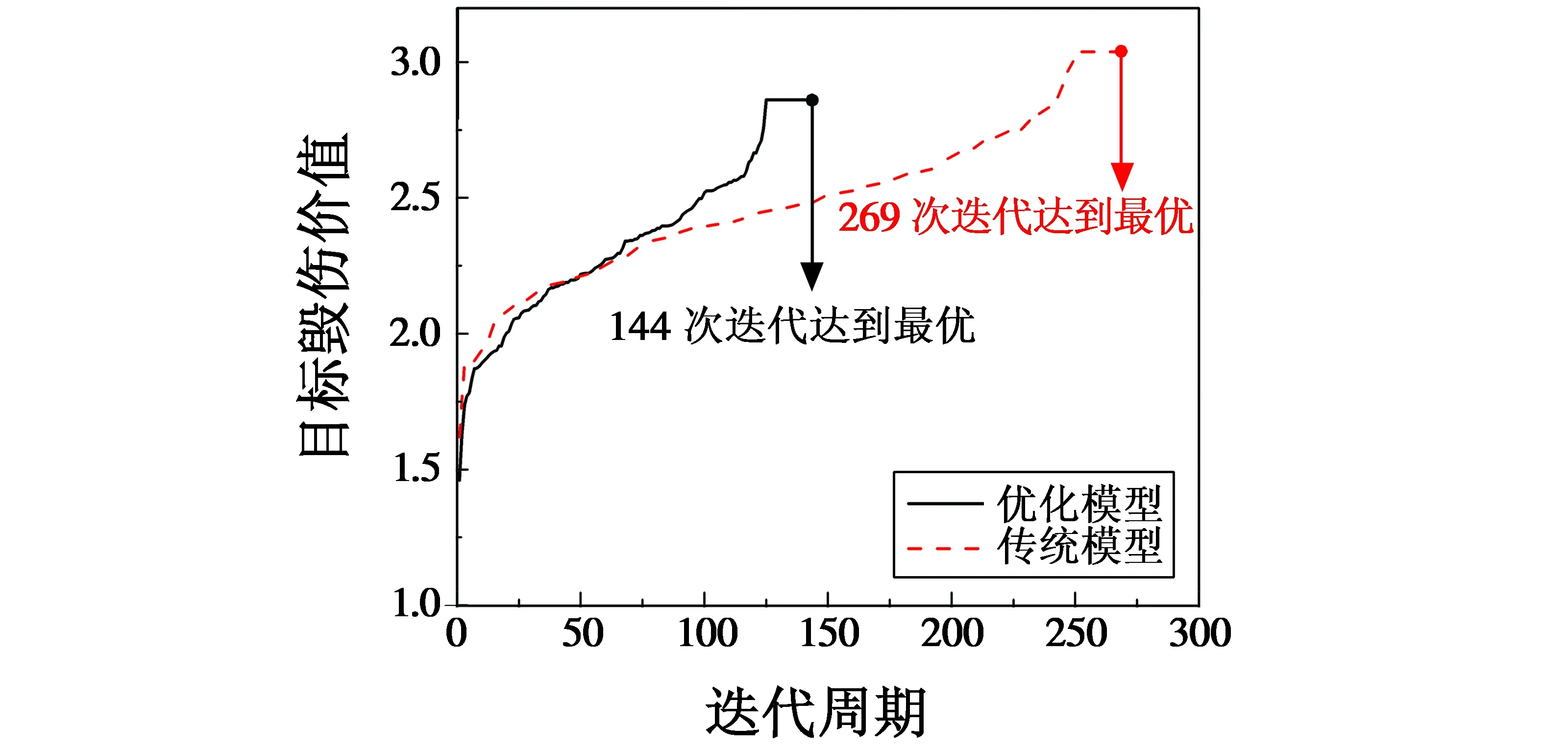
传统武器目标分配问题是以武器对目标的最大毁伤价值为目标函数建立模型[8]。假设防控区部署m套拦截武器,某时发现n个目标(n (1) 式中,ei j表示武器i对目标j的拦截概率。 用矩阵X表示武器与目标的打击分配决策,即 (2) 式中,xi j∈{0,1},xi j=1,表示武器i拦截目标j,否则两者不形成拦截关系。 显然武器i成功拦截目标j的概率可表示为 pi j=1-(1-ei j)xi j。 (3) 目标j被成功拦截的概率可表示为 (4) 因此,使用现有武器成功拦截全部目标的概率为 (5) 以上过程是假设每个目标自身的威胁度相同,因此没有进行目标的优先级排序。引入μj作为目标j的威胁系数,得到基于最大毁伤价值的传统武器目标分配模型为 (6) 式中:i=1,2,…,m;j=1,2,…,n。约束条件①表示同一时刻,单个武器只能拦截一个目标;约束条件②表示每个目标分配的武器数量不超过该类型武器总数量;约束条件③表示决策矩阵中的元素只能取1或0,意味着武器和目标仅存在拦截和非拦截关系。 传统单一体制的武器目标分配模型是从决策矩阵的有效性方面建立约束,但在多体制复合拦截过程中,武器还受到技术性能指标的约束,因此还需要考虑作战效能及战场环境等方面对分配模型的影响[11]。为更好地解决该问题,本文引入武器拦截权重因子qi j来描述武器i对目标j进行拦截的可行性,定义如下 (7) 该因子的确定需要综合考虑目标运动规律和位置、拦截武器的技术性能限制等因素。本文将对该因子的分析抽象为空间、时间、资源及环境4个维度进行衡量。 1.2.1 空间约束条件 武器拦截受空间作战距离的限制,即目标需在武器的火力范围之内。记di j为武器i到目标j的欧氏距离,himin和himax分别为武器的拦截下限和上限,判断武器实施拦截是否满足空间约束条件,即 himin≤di j≤himax (8) 1.2.2 时间约束条件 武器拦截时同样受作战响应时间的影响,即武器从收到作战指令到实施拦截的时间间隔应小于目标在防控区内的飞行时间。假设目标来袭方向固定,且在短时间内速度不变,根据目标在防控区内的飞行距离与速度之比计算其飞行时间,并与拦截武器响应时间比较,建立时间约束关系。 图1所示为目标穿过3种拦截武器防控区的示意图,根据目标终点与防控区的关系分为两种情况。其中,O是防控区中心点,Q(ρ,θ)是武器部署坐标,r1和r2分别是武器拦截下限和上限,目标以飞行速度v进入防控区,s是武器与目标的欧氏距离。根据装备的拦截特性,目标在各武器防控区的飞行轨迹标记为AB(距离为L)。 图1 3种武器的拦截示意图Fig.1 Interception schematic of three kinds of weapons 判断武器实施拦截是否满足时间约束条件,即 (9) 根据图1(a)~1(f)几何关系,L可分别表示为 (10) 1.2.3 资源约束条件 武器剩余弹量会随战斗的进行而不断减少,因此需在武器分配决策前检查各武器的可用性。对于激光和无线电装备,资源约束主要指武器的剩余时间是否可以实施一次拦截;对于柔性网装备(每套可发射4发网弹),资源约束条件表示为 (11) 1.2.4 环境约束条件 当战场的湿度、可见度、风力等环境状况不理想时,会影响武器的拦截效能,降低目标的拦截概率。引入环境约束条件表征武器的作战效能。当战场环境理想,各武器可充分发挥其拦截效能;当风力达到5级以上时,柔性网的拦截性能降低30%;当空气湿度大于80%或可见度低于80%时,激光武器的拦截性能降低30%。因此,针对各种拦截武器作战效能,定义环境约束条件为 (12) 基于以上分析,武器i与目标j的拦截权重因子定义为 (13) 式中,&表示“与”运算。 在传统武器目标分配模型中引入武器拦截权重因子,建立用于“低慢小”目标武器分配优化模型为 (14) 式中:i=1,2,…,m;j=1,2,…,n。 “低慢小”目标的火力分配问题属于非线性规划(NP)问题,本文采用遗传算法对该问题进行求解[12-16]。首先,将解向量作为染色体进行编码,并随机生成一定规模的初始种群;然后,根据遗传算子对种群中的个体进行选择、交叉及变异等操作;最终,通过迭代逐渐演化出适应度最高的个体,作为模型的最优解。具体过程如下。 1)初始化种群。为直观地观察分配结果,将目标武器分配方案作为染色体,采用实数编码方式进行编码,并随机生成N个满足约束条件的个体作为初始种群,进行后续遗传操作。 2)适应度函数定义。目标火力分配的目的是使作战效能达到最大,而本文提出的模型正是基于使目标毁伤价值达到最大而建立的,因此将模型的目标函数直接作为适应度函数。 3) 遗传操作。首先采用轮盘赌法对种群个体进行选择,使适应度值较高的个体保留到下一次迭代的概率更高。然后对种群中个体分别采用有序交叉法[14]进行交叉操作,以保证种群的稳定性,使迭代过程向着最优解方向进化。最后以一定概率进行变异操作,保证种群多样性,避免计算结果陷入局部最优解。 4) 终止条件判断。对种群个体重复进行遗传操作。若迭代次数达到预设最大值,或达到稳定迭代周期(即最优个体在一定迭代周期内不发生变化),则结束进化,选择最大适应度值对应的个体作为最终计算结果。 “低慢小”目标武器分配流程如图2所示。 首先通过探测设备获得来袭目标的基本信息,计算武器拦截权重因子,建立“低慢小”目标多体制武器分配优化模型并使用遗传算法进行求解,最终得到火力打击决策方案。 假设我方阵地分别部署激光1套(W1)、无线电设备1套(W2)、柔性网设备2套(W3,W4)共计4套拦截武器用于抵御“低慢小”目标袭击,各武器的剩余弹量充足。某日监测到4个“低慢小”目标情报,需对其进行打击。武器信息、目标信息及拦截概率矩阵分别如表1、表2和表3所示。其中,W2和W4武器受该位置天气因素的影响,作战性能分别下降至0.7。目标威胁值的评估是利用层次分析法和动态贝叶斯网络分别对定量因素和定性因素进行量化计算,最终综合评估得到目标威胁值[17]。 表1 部署武器信息Table 1 Information of the deployed weapon 表2 来袭目标信息Table 2 Information of the attacking targets 表3 武器目标拦截概率Table 3 Interception probability of weapons to targets 分别使用传统武器分配模型及本文提出的优化模型进行计算,设定种群大小为20,选择概率为0.9,变异概率为0.01,最大迭代次数为500,稳定迭代周期为20。 毁伤价值演化曲线如图3所示。传统模型和优化模型均因达到稳定迭代周期而停止计算,说明两个模型均已收敛到最优解。从总迭代次数上看,传统模型的迭代次数远多于优化模型,这是由于后者引入了武器拦截权重因子,提高了对武器目标分配方案的约束,导致其可行解的总数量小于传统模型可行解的总数量,因此相同训练周期内优化模型得到最优解的概率更高,这也说明该因子的引入提高了分配方案的求解效率。从毁伤价值上看,武器拦截权重因子的引入导致了模型目标函数表达形式的变化,这说明相同分配方案对应两个模型计算的毁伤价值数值不相同,意味着毁伤价值的数值可作为同一模型内个体间优劣评价的依据,但对于不同模型个体间的评价无参考意义。 图3 毁伤价值演化曲线Fig.3 Evolution curve of damage value 最终得到的武器目标分配方案如表4所示。 表4 武器目标分配方案Table 4 Weapon assignment to targets 可以看出,两个模型的最优分配方案不一致。根据前文分析可知,目标T3在武器W4防控范围内的逗留时间为1.49 s,小于该武器3 s的作战响应时间,说明目标会在拦截武器发射前飞出其防控区,导致拦截失败。因此,该分配方案不具备可行性。本文提出的优化模型在决策分配方案时加入了武器拦截权重因子,排除了武器启动拦截时目标飞出防御范围的可能,保证了武器的作战效能,提高了分配决策的可靠性和合理性。因此,本文提出的武器分配方案在实际作战中具有更大的指导意义。 本文针对“低慢小”目标多体制复合拦截技术中的武器目标分配问题展开研究。分析了激光、无线电及柔性网3种拦截武器在空间、时间、资源及作战环境4个维度的约束条件,在传统武器目标分配模型中引入了武器拦截权重因子,并基于此提出了用于“低慢小”目标的武器分配优化模型。通过仿真算例并将结果与传统模型计算结果对比,验证了本文所建的优化模型具有更高的计算效率及更大的可行性,计算得到的分配方案具有更强的实际应用价值,可为多体制武器目标火力分配问题提供很好的解决思路。1.2 “低慢小”目标武器分配优化模型

2 模型的求解
3 算例仿真
3.1 实验想定
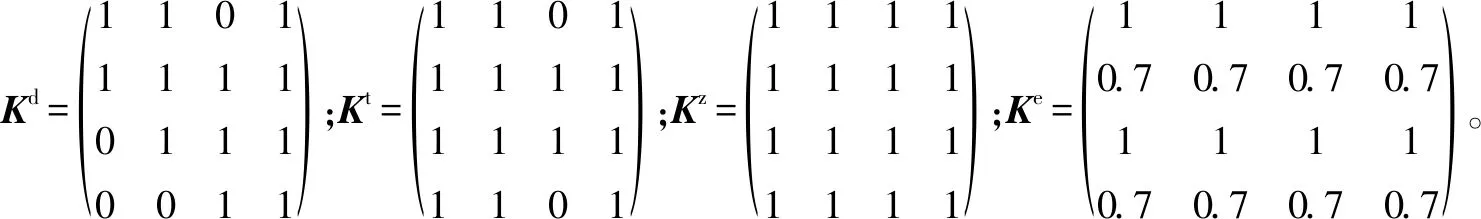
3.2 仿真结果

4 结束语
