基于超声高阶兰姆波的薄板应力测量技术研究

原 帅,赵晓春，廖 林，禤伟明，袁懋诞

(1.内蒙古电力科学研究院，内蒙古 呼和浩特 010020;2.广东工业大学 机电工程学院，广东 广州 510006)

0 引言

金属薄板是现代制造最常见的结构，在许多机械系统中都承担着关键的角色。薄板结构的失效会造成巨大经济损失，严重时甚至会威胁到人民的生命安全。其中，薄板中应力是其功能失效的主要诱因之一，包括外部应力和残余应力，外部应力取决于其他机械构件的相互作用，而残余应力则通常是构件在加工制造过程中产生的弹性应力[1]。目前应力检测技术可分为有损和无损检测[2]，其中有损检测技术有盲孔法[3]、切条法[4]、压痕法[5]等，无损检测技术包括X线衍射法[6]、超声波法[7]等。超声波法由于具有高分辨率、高渗透力和对人体无伤害等特点，成为应力无损检测发展方向上最有前景的技术之一。

超声波应力测量是基于材料弹性极限内的声弹性原理，即构件中存在应力时会改变超声波在构件中的传播速度。现有超声波应力检测技术主要包括表面波法[8]、体波法[9-10]及临界折射纵波法[11]。其中，临界折射纵波法因其对应力具有较高的灵敏度，故应用最广泛，同时，临界折射纵波还可穿透到表面以下一定深度，且随深度呈指数衰减，该特性可以用于检测构件近表面的应力随深度的梯度变化。Javadi等[12-14]使用一系列不同频率的超声传感器测量钢板和焊接钢管内部不同深度下的残余应力，测量结果与盲孔法和有限元法的验证结果具有较好的一致性；Sadeghi等[15]利用临界折射纵波法测量经过搅拌摩擦焊加工的铝板中残余应力，并通过有限元仿真验证了其测量结果；Li等[16]使用临界折射纵波法测量结构钢件内部的绝对应力，实验结果与应变计测得的结果吻合。由于该技术受限于纵波速度和频率，使得临界折射纵波只在结构表面和近表面传播，不适用于薄板结构中整体应力的测量。

超声兰姆波是在板状结构传播的导波，可长距离传播且模态众多，广泛应用于薄板结构的大范围检测和监测中。目前关于兰姆波的声弹性效应理论研究较少，Husson[17]从理论角度研究了兰姆波的声弹性效应，并预测兰姆波的声弹性常数对于频率具有很强的依赖性；Mohabuth等[18]研究了均匀应力对兰姆波传播的影响，并提出高阶兰姆波模态在截止频率附近时，对于所施加的应力具有较高的灵敏度，且随着频率的增加，灵敏度慢慢降低并趋于稳定；Shi等[19]利用空间分布的压电片阵列测量双轴应力下与应力方向呈不同角度的兰姆波相速度的变化量；Pei等[20-21]研究了高阶兰姆波对平行和垂直载荷的敏感性，发现在铝板中S1模态对应力测量具有高敏感度；Gandhi等[22]结合声弹性理论和兰姆波在各向异性薄板中传播理论，推导出了双轴应力影响下兰姆波的声弹性方程。由于应力引起的超声波声速变化非常微小，所以提高其灵敏度是超声应力检测研究的重要工作之一。为提高超声法对薄板应力的测量精度，本文提出了基于高阶兰姆波的应力测量技术。

1 兰姆波声弹性效应的基本理论

1.1 兰姆波的频散特性

兰姆波是在板状结构中传播的导波，在传播过程中，其声速会随着频率而改变，这一现象称为频散效应。薄板中的兰姆波存在多种模态，可由瑞利-兰姆方程表示，假设薄板介质无限大，薄板上下边界自由，其对称和反对称模态[23]分别为

(1)

(2)

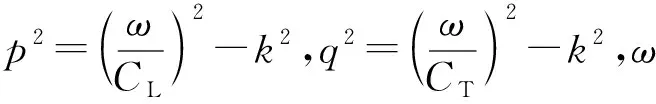
(3)

(4)

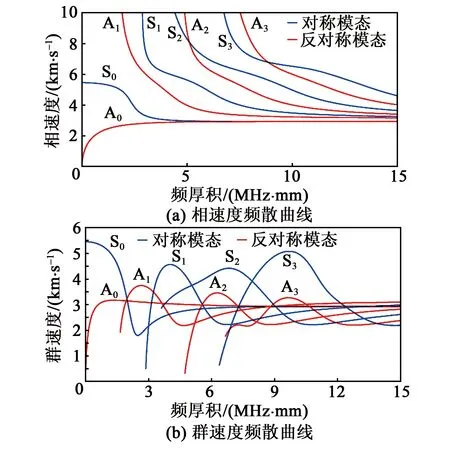
图1 铝合金薄板的频散曲线

由图1可知，不同频厚积下的兰姆波群速度和相速度是变化的，但随着频率不断增大，各模态的速度都会趋向稳定。当频厚积小于1.5 MHz·mm时，薄板中仅存在A0和S0两种基本模态，随着频厚积增大，薄板中存在的兰姆波模态数量逐渐增加。因此，想要激励单一的兰姆波低阶模态，应选择较小的激励频率，若要激励高阶兰姆波模态，则需要选择较高的频率。

1.2 基于Floquet-Bloch(F-B)理论的兰姆波声弹性频散分析模型

基于Floquet理论的波动有限元法已成功应用于不同结构的超声波频散特性分析[24]。通过分析周期性结构单元，搜寻波数-频率对，可以计算不同波导模态的频散曲线，计算原理如图2所示。由于其几何模型、材料模型和边界条件的可调性，该方法非常适用于分析复杂波导结构和材料模型。针对薄板结构中的初始应力状态，波动有限元法可有效获得任意应力状态下兰姆波的频散特性。本文利用有限元软件COMSOL的固体力学模块，建立频散分析模型研究兰姆波的声弹性效应。薄板材料为铝合金，其密度ρ=7 850 kg/m3，杨氏模量E=73.5 GPa，泊松比ν=0.336，纵波声速CL=6 370 m/s。在单元x方向左右施加基于F-B理论的周期性边界，其数学表达式为

udst=usrce-ik(rdst-rsrc)

(5)

式中：u为位移；dst和src分别表示终点平面和起始平面；r为距离。对于微小的单元模型，在给定的k下通过固体力学模块的特征频率求解器，计算出对应的特征频率f，通过扫描每一个k下对应的f，获得一系列k-f对数据。以四边形映射对计算区域进行网格划分，为满足收敛条件，网格最小边长设定为lx/3，lx为x方向的建模长度。

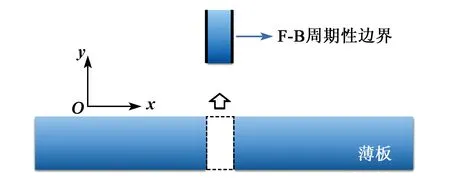
图2 兰姆波频散计算模型

为使结果精确可靠，需要考虑初始应力带来的非线性变化，因为即使是在极小的形变下，由于高阶弹性常数的影响，应力和应变之间会存在非线性关系。当形变较大时，非线性关系会带来较大的影响。若忽略高阶常数，则会给模型仿真结果带来较大的误差。为了提高模型的准确性，将单元模型的材料模型设置为超弹性材料中的默纳汉超弹性材料模型[25]。默纳汉超弹性材料模型的应变能密度函数的表达式为

2m)I1(ε)3-2mI1(ε)I2(ε)+nI3(ε)

(6)

式中：I1、I2、I3分别为弹性格林-拉格朗日应变张量；λ和μ为二阶拉梅常数；m、n和l分别为三阶默纳汉弹性常数。通过稳态施加预载荷的步骤，可以将拉伸或压缩应力引入模型中。因此，基于该材料模型的频散分析模型可以用于分析任意应力下兰姆波的声弹性效应。

1.3 各模态声弹性效应分析

通过建立基于F-B理论的兰姆波声弹性频散分析模型，研究了100 MPa拉应力和无应力下兰姆波相速度频散曲线变化。为观察各模态声速变化规律，绘制了S0、S1、A0、A1模态在100 MPa拉伸应力下相速度变化的频散曲线如图3所示。由图可知，S0和A0模态在频厚积靠近0处的相速度变化量最大，随着频厚积的增大而逐渐稳定，S0模态的相速度变化量均处在相对较小的值内。S1、A1兰姆波高阶模态均存在截止频率，在截止频率附近，高阶模态受应力影响最明显，随着频厚积的增大，相速度变化量先是急剧降低，随后缓慢减少至平稳。因此，为了提高兰姆波对应力的敏感度，应在截止频率附近激励高阶模态。

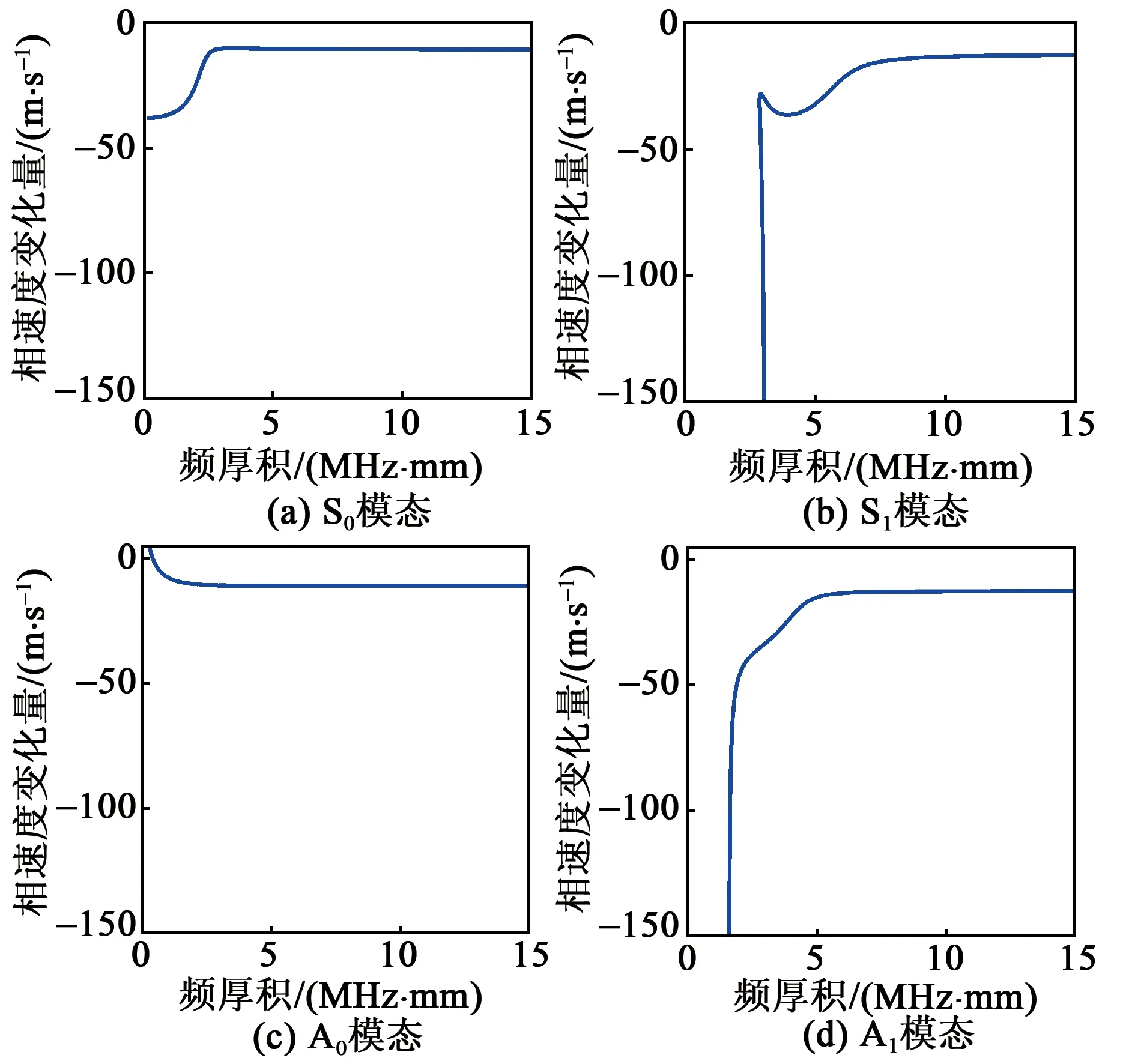
图3 100 MPa均匀应力下各模态兰姆波相速度变化

2 超声兰姆波实验系统

2.1 基于斜入射法的兰姆波系统

图4为基于斜入射法搭建的超声兰姆波检测系统，利用该系统可以在薄板中激励和接收各阶兰姆波模态。函数发生器中产生激励信号，激励信号经过脉冲放大器放大后传送给发射探头。发射探头以一定倾斜角度发射超声信号，信号经过楔块进入被测薄板中，并在薄板中以兰姆波形式传播到另一个楔块被接收探头接收，将超声信号显示和保存在示波器中。为准确测量应力引起的声速变化，应保证声波传播距离始终保持不变，避免由于传播路径发生变化而引起传播时间的改变。因此，本实验设计了一块矩形固定框，通过螺丝将楔块对固定在框内，保证实验过程中楔块间的相对距离，如图5所示。为激励特定模态兰姆波，楔块角度需要满足斯涅耳定律：

sinθ=C/Cp

(7)

式中：θ为声波入射角；C为楔块中的纵波声速；Cp为对应模态兰姆波的相速度。当C=2 337 m/s时，可得入射角频散曲线，如图6所示。由图6可知，在一定频厚积下通过调整θ，可在薄板中激励出不同模态的兰姆波。

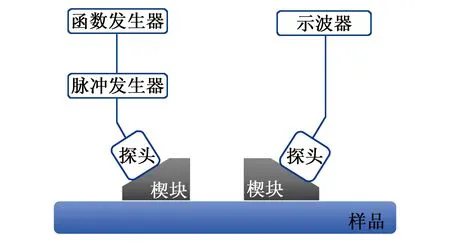
图4 基于斜入射法的超声兰姆波系统示意图

图5 楔块式兰姆波超声传感器

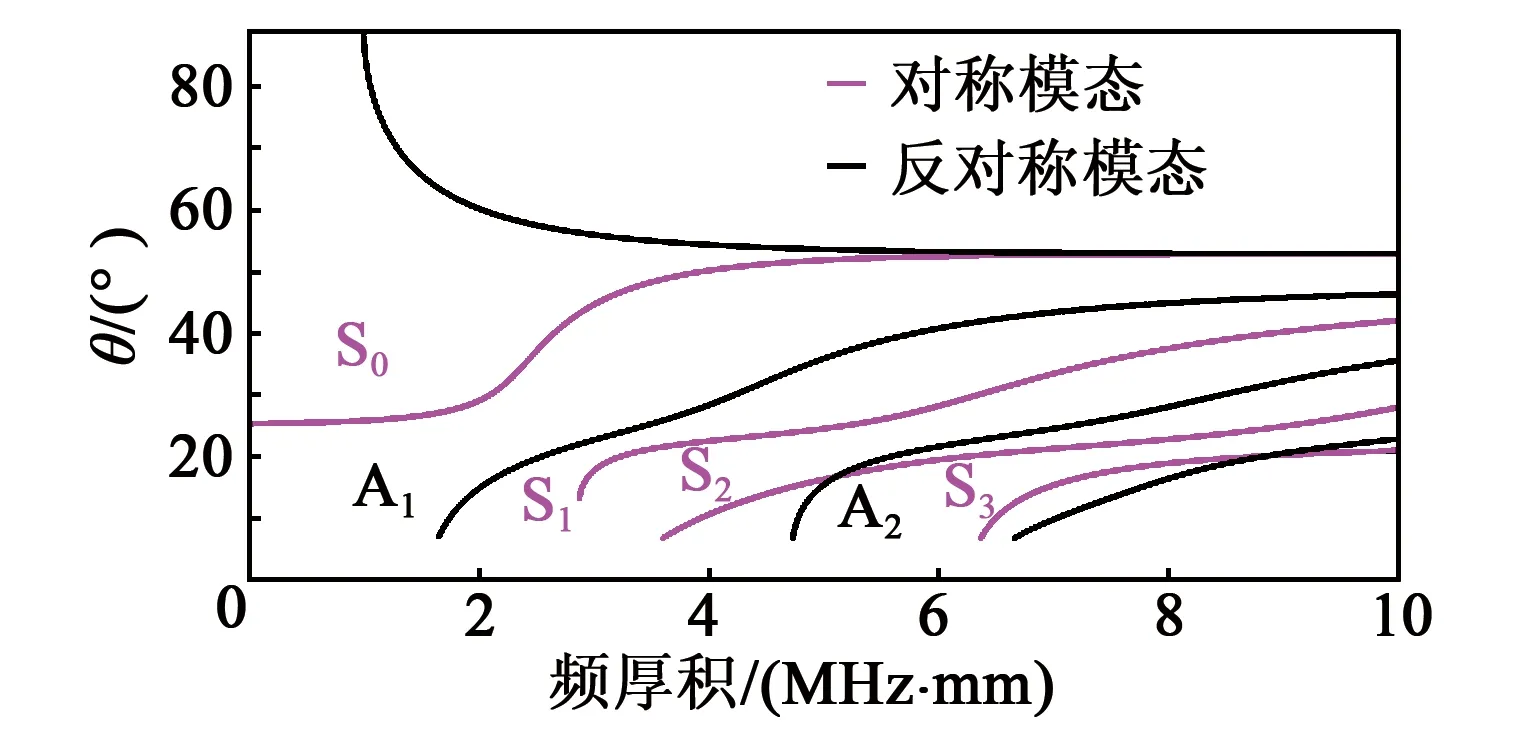
图6 兰姆波入射角频散曲线

2.2 高阶兰姆波选择激励

为验证超声兰姆波系统的高阶兰姆波激励和接收效果，本文采用短时傅里叶变化在时频域中进行模态识别。楔块的间距为11 cm，将探头楔块组合置于厚为3 mm的铝板上，激励信号是中心频率为1 MHz的5个周期正弦信号，入射角为25°时接收信号如图7(a)所示，时域图中90 μs附近存在一个高能量波包，在100 μs后为一串连续的信号，将信号进行短时傅里叶变换，结果如图7(b)所示，振幅最大的波包属于兰姆波A1模态，而后续的连续信号为截止频率附近的S1模态。因此，通过该兰姆波系统，可以在铝板中激励出所需的高阶兰姆波信号，以用于应力测量。

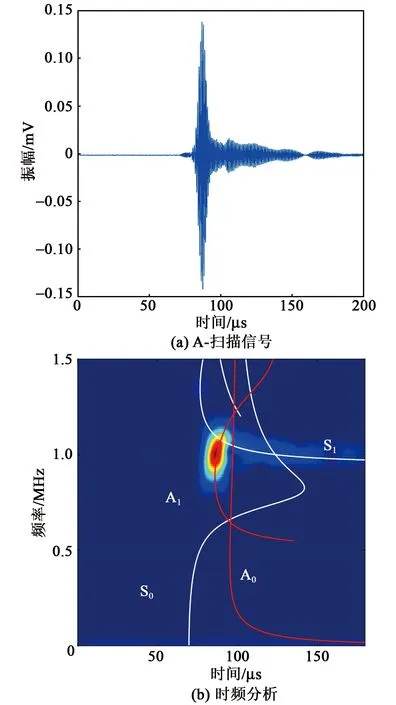
图7 A1模态的A-扫描信号及其时频分析

3 超声兰姆波实验系统

3.1 标准拉伸试验

为实现兰姆波应力测量，需要利用上述超声兰姆波系统对标准加载试样进行应力测量。本文通过拉伸机对均匀薄板试样进行标准拉伸而产生内部应力，如图8所示。将均匀试样固定在拉伸机中，通过G型夹将探头和楔块固定在薄板中。按照第2.2节所述调整探头入射角，在薄板样品中激励出A1模态信号，为了准确识别出声波在固定传播距离下传播时间的微小变化，示波器的采样率设置为2 GHz，采样平均次数设置为256，拉伸机加载拉力的速度设置为0.1 kN/s，待拉力增加量达到3 kN时，停止增加拉力，并维持当前的拉伸状态。30 s后待薄板内部稳定后保存接收探头接收到的信号。信号保存完毕后重复同样的步骤，保存0～18 kN拉力下的超声信号，并将拉力换算为应力。

图8 标准拉伸试验系统及均匀薄板试样

3.2 应力标定

为实现应力测量，需要通过应力标定实验，获得应力与时间差之间的定量关系。图9为无应力与200 MPa拉伸应力下A1模态信号对比图。由图可知，受拉伸应力的影响，A1模态的到达时间会稍微延迟，表明A1模态的群速度减小，这与兰姆波声弹性理论符合。取不同应力下A1模态信号峰值所在时间点，并与无应力下信号峰值时间点作差，得到不同应力下时间变化量如图10所示。基于最小二乘法得到应力δ=1 509.842×Δt+2.205。利用该标定关系可以实现A1模态的应力测量。

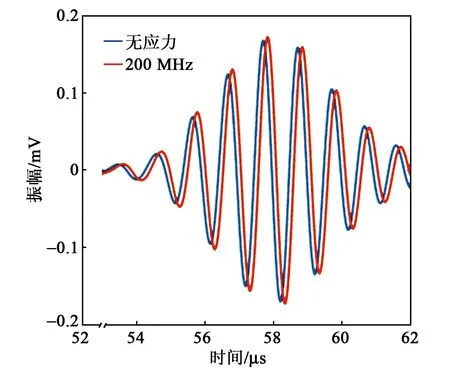
图9 无应力和200 MPa拉伸应力下A1模态信号变化

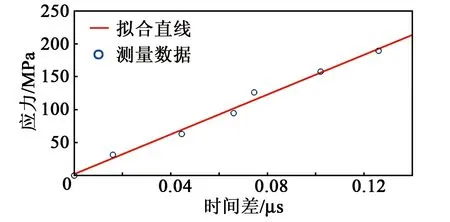
图10 A1模态传播时间变化随应力变化

3.3 不均匀试样应力测量

为进一步验证A1模态的应力测量效果，本文设计了一个厚度为3 mm的变截面试样，利用拉伸机在两端施加6次不同的特定拉力，造成不同应力状态，如图11所示。在位置A、B两端由于宽度不同而产生不同的特定应力，且在A、B区域交接处的应力变化显著，需要采用小型超声传感器和高精密时间测量装置进行测量。故利用第3.2节中A1模态标定结果在位置A、B两端均匀位置测量的应力结果与实际应力对比如图12所示。由图12可知，不同状态下，A1模态的测量结果与实际应力吻合，其中，位置A端的最大误差为7.03 MPa，位置B端最大误差为11.73 MPa。实验结果表明，兰姆波A1模态能够准确地测量薄板中的应力。

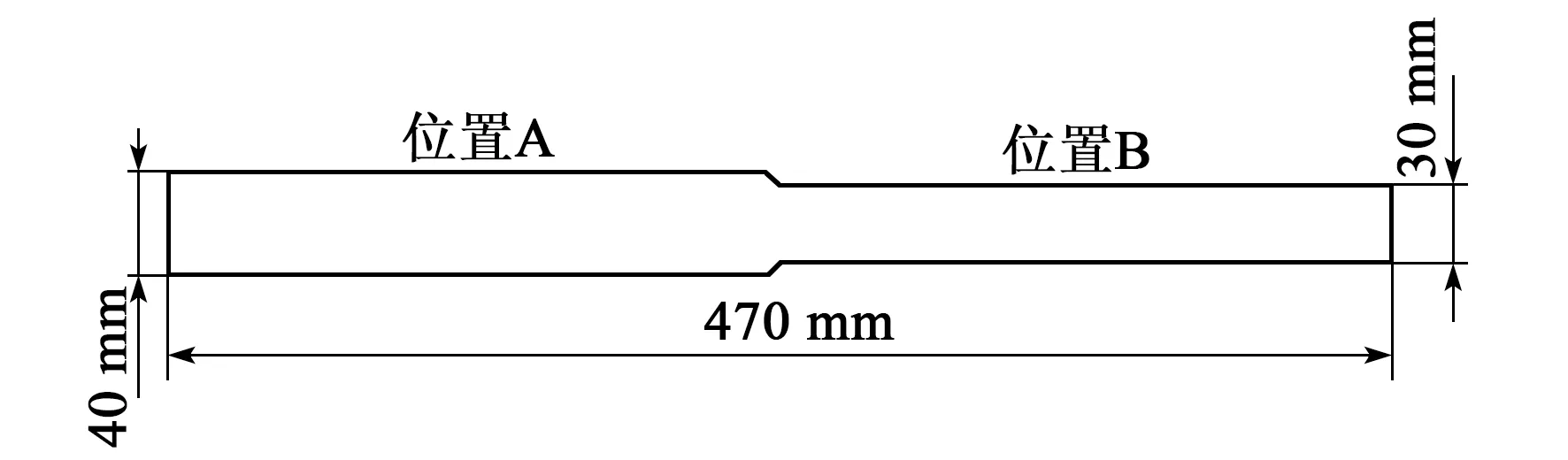
图11 变截面试样

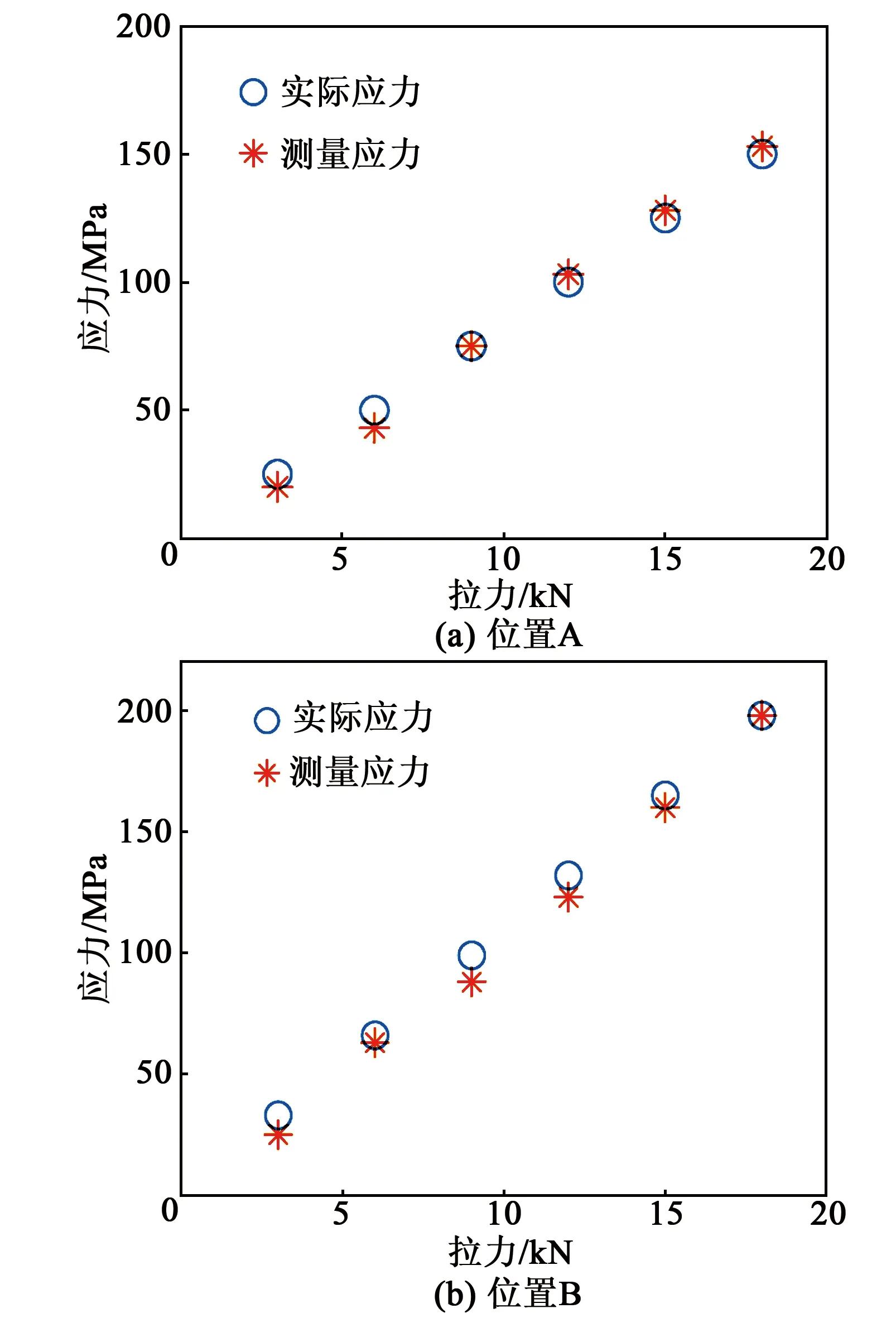
图12 变截面试样的A1模态应力测量结果

4结论

本文针对薄板应力检测问题，对高阶兰姆波的薄板应力测量技术进行了研究。从兰姆波声弹性效应出发，基于F-B理论模型，研究了应力下各模态频散曲线的变化。基于斜入射法搭建超声兰姆波检测系统实现高阶兰姆波A1模态的激励，并利用标准拉伸实验，获得了A1模态的应力标定曲线。最后在不均匀薄板上不同应力区域对A1模态的应力测量效果进行了验证。从理论和实验两部分验证了该技术的可行性，主要得到如下结论：

1) 基于F-B理论和超弹性材料模型建立了兰姆波声弹性效应分析模型，获取了兰姆波不同模态在应力下的频散曲线变化。结果表明，兰姆波低阶模态对应力的敏感性较低，而兰姆波高阶模态在截止频率附近对应力具有较高的敏感度。

2) 通过标准拉伸实验，利用斜入射兰姆波系统激励高阶兰姆波信号，可以获得兰姆波各模态的时间变化与应力间的标定关系。基于A1模态实现了变截面薄板中不同位置的应力测量，测量误差均在15 MPa以内，表明高阶兰姆波模态可用于薄板内部应力精确测量。

本研究还将进一步研究不同模态的应力测量及非接触式检测技术的薄板应力场分布测量。