核心素养下数学史融入高中等差数列的教学策略研究

摘 要：等差数列是高中数学的重要内容之一，蕴含丰富的数学核心素养。而数学史作为数学文化的一个重要组成部分和具体表现形式，蕴含丰富的数学思想，在培养学生的核心素养方面发挥着重要作用。因此，本文首先将分析出等差数列的教学内容侧重培养的数学核心素养;其次分析等差数列中存在的数学史内容及其教育价值;最后基于以上两个方面的分析，提出高中数学等差数列这一课时融入数学史的教学策略。

关键词：数学史 等差数列 核心素养

1 引言

高中阶段是学生发展的一个重要的阶段，在这个阶段的教学中加强对学生数学核心素养的培养，对于促进学生全面发展具有重要作用。同时在《普通高中数学课程标准（2017版）》（简称《标准》）明确了数学核心素养之后，数学教育研究者们更加关注对学生数学核心素养的培养。而数学史注重数学知识产生与发展的历程，蕴含了丰富数学思想，以数学史材料为素材，在进行具体的教学时将这些数学史素材与数学知识相结合，可以有效地培养学生的数学核心素养。

朱立明在《核心素养视角下数学史教育的价值与策略》中认为数学史具有教育价值，并从三个方面提出实施策略[1];高山在《探讨数学史对提高高中学生数学核心素养的价值和策略》结合高中数学教学的情况，探讨数学史对提高高中学生数学核心素养的价值和策略[2];赵虎在《浅谈数学学史对提高高中学生核心素养的价值》主要人格形成、数学能力强化、增长知识见识三个方面，谈数学史对培养学生数学核心素养的价值，最后提出教学策略[3]。以上文献分析了数学史对于培养学生核心素养方面具有的教育价值并提出相应的教学策略。但是在具体的课程内容方面研究较少，尤其是关于高中等差数列这一方面的研究还不够全面。

由此，本文将分析等差数列侧重培养的数学核心素养以及等差数列中存在的数学史内容及其教育价值，最后结合以上两个部分的内容提出高中数学等差数列这一课时融入数学史的教学策略。为该领域的研究在理论和实践方面提供参考。

2 核心概念的界定

对于核心素养和数学史的研究已经有一定的历史。在数学史方面，从19世纪中叶开始，教育研究者们就已经开始关注数学史和数学教育之间的关系。而在核心素养方面，《标准》中提出数学核心素养的概念。

2.1 数学核心素养

对于数学核心素养的概念的研究有很多，不同的专家学者有不同的理解，而且都有它们的合理性。而《标准》经过专家多年的研讨，并且在征求了广泛的意见之后编订的。其关于数学核心素养概念的界定具有一定的权威性。由此本文采用《标准》中对于数学核心素养概念的界定：数学核心素养是数学课程目标的集中体现，是具有数学基本特征的思维品质、关键能力以及情感、态度与价值观的综合体现，是在数学学习和应用的过程中逐步形成和发展的[4]。

2.2 数学史

数学史是研究数学科学发生、发展及其规律的科学。它研究数学内容、思想和方法的发生、发展过程，也研究可能影响这种过程的因素，以及数学的发展对人类文明所带来的影响。

3 核心素养下高中数列内容分析

上面已经对数学核心素养的概念做了介绍，本节将以《标准》中六大数学核心素养的内涵为基础，结合高中等差数列的具体教学内容，分析高中等差数列的具体教学内容侧重培养的数学核心素养。

数学抽象是指通过对数量关系与空间形式的抽象，得到数学研究对象的素养[4]。而在等差数列的教学中，如在向学生讲解等差数列的概念时，教师可以利用生活或其他方面设计问题情境，引导学生对问题情境中涉及到的数列进行分析，归纳规律，从中抽象出等差数列的概念，培养学生数学抽象素养。此外等差数列的性质及其应用、等差数列前n项和公式，同样可以培养学生数学抽象素养。

逻辑推理是指从一些事实和命题出发，依据规则推出其他命题的素养[4]。很多性质、法则、公式、定理的推导，都是建立在定义或命题上，并通过逻辑推理得出的。而在等差数列的教学中，如向学生讲解等差数列通项公式的推导时，教师可以向学生提出这样一个思考：你能根据等差数列的定义推导它的通项公式吗？引导学生利用等差数列的定义推导其通项公式。除此之外，还可以引导学生寻找其他的方法推导出等差公式的通项公式。在这个过程中学生仔细观察，利用已有定义，通过严密的推理得出结论，培养学生的逻辑推理素養。此外等差数列的性质的推导及其前n项和公式的推导，同样可以培养学生的逻辑推理素养。

数学运算是指在明晰运算对象的基础上，依据运算法则解决数学问题的素养[4]。而在等差数列的教学中，如向学生讲解等差数列的应用时，教师可以设置相关的典型例题，引导学生在解决问题的过程中，首先明确问题考查的对象，其次选择等差数列的相关知识，最后按照运算的基本程序解决问题，培养学生的数学运算素养。此外等差数列的通项公式、等差数列的性质的应用，同样可以培养学生的数学运算素养。

数学建模是对现实问题进行数学抽象，用数学语言表达问题、用数学方法构建模型解决问题的素养[4]。而在等差数列的教学中，如利用等差数列解决实际问题，可以使等差数列从教材中的理论知识转化成为实际生活中的可操作计算方法，以此来培养学生数学建模思想。

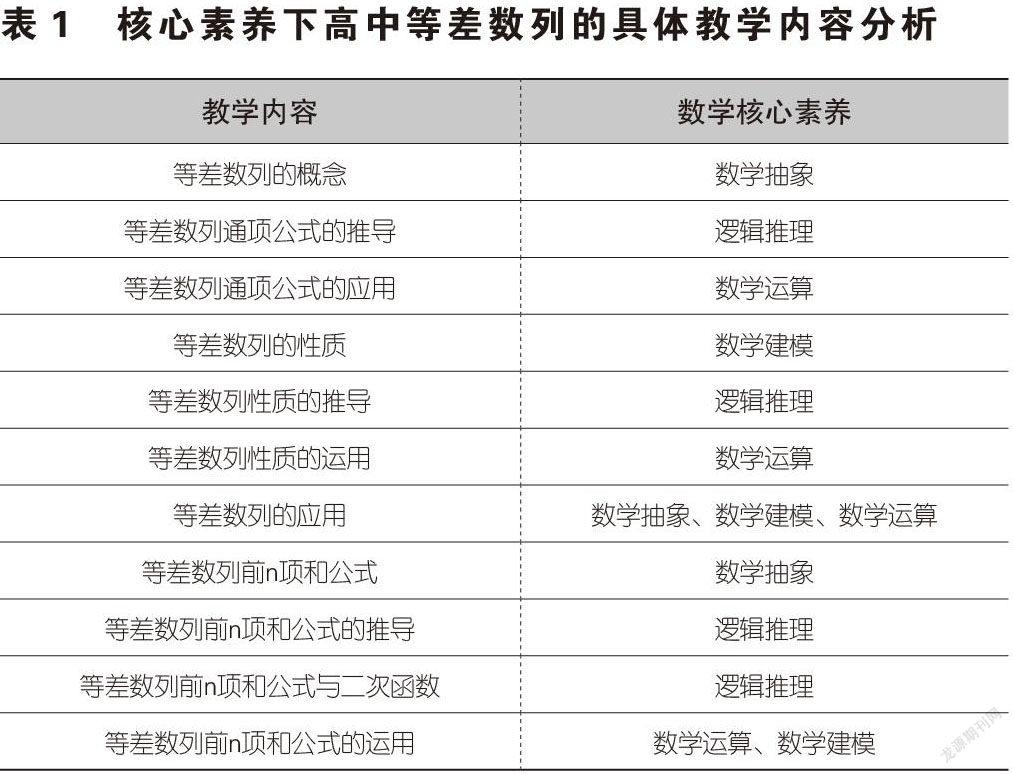
通过以上的分析，得到高中等差数列的具体教学内容侧重培养的数学核心素养，具体情况如表1：

表1详细地展示了等差数列的具体教学内容侧重培养的四个数学核心素养，包括数学抽象、逻辑推理、数学运算和数学建模。而对于以上的具体教学内容中未提及的数学核心素养，并不是指这部分的具体教学内容一定不能培养该数学核心素养，而是指这部分的教学的具体内容也可能培养该数学核心素养，只是相对于对其它的数学核心素养的培养来说较弱，因此没有提及。

4 高中等差数列数学史内容分析

在等差数列的教学上，一定程度地介绍等差数列发展的历史有助于帮助学生树立健全的数学观和培养学生的数学核心素养。因此以下部分将分析等差数列涉及到的数学史内容，并分析其在数学教学方面发挥的作用。

4.1 数学故事

在等差数列发展的每一个时期都充满了众多精彩的数学故事，有许多典型的数学故事值得向学生介绍。例如，高斯、丢番图、杨辉等数学家的生平轶事。本节主要列举“高斯求和”的故事：高斯是德国著名数学家，在他10岁时，他当时的数学老师布特纳出了一道算术题“求1+2+3+…100的和”，布特纳刚叙述完题目，高斯就很快算出了正确答案。在教学过程中适当的向学生讲授数学故事，一方面可以吸引学生的注意力，增强学生的学习兴趣;另一方面可以拉近学生与数学家的距离，更真切地感受数学家们对数学热情，培养学生对数学的热爱。

4.2 数学家的思想方法

在等差数列发展中产生了无数的思想方法，它们都是数学家们智慧的结晶。在等差数列思想中具有代表性更是举不胜举，例如：欧拉“错位相减”法、列方程求解等差数列问题、阿尔·卡克希撰写的《代数之荣耀》中有关等差数列求和问题的解法等。本节主要列举阿尔·卡克希撰写的《代数之荣耀》中有关等差数列求和问题的解法：书中记载1+2+3+…+n=，阿尔·卡克希用倒序相加法证明了上述命题，并且把这种方法用于一般的等差数列求和。在教学过程中通过介绍数学家的思想，让学生了解它、认识它，一方面可以开阔学生的思维;另一方面还能让学生近距离地了解它们，以此来贴近数学家的思想，看到他们为真理所付出的艰辛，以此为榜样给学生前行的力量。

4.3 数学著作

在等差数列发展的历程中产生了无数数学著作，它们是数学史的重要组成部分之一。《周髀算经》、《九章算术》、《孔子算经》、《张邱建算经》等著作中都包含了等差数列的相关运用和计算方法，其中以《九章算术》中等差数列的运算记载最为系统。例如，《九章算术》中《盈不足》第19题、《衰分》第1题、《均输》第17题、第18题都是很好的教学资料，经过一定的改编可以应用到具体的教学过程中。这些著作中丰富的资料，一方面可以让学生更进一步的了解等差数列概念产生的背景，形成感性认识;另一方面，可以吸引学生的注意力，增强学生的学习兴趣。

5 核心素养下数学史融入高中数列的教学策略

数学史在培养学生的数学核心素养方面发挥了重要的作用，因此教师在教学过程中可以将数学史料充分地融进课堂中。下面将在等差数列的数学史内容的基础上，结合核心素养下高中等差数列的教学内容，具体论述如何将数学史融入到教学过程。

5.1 利用数学故事创设教学情境，培养学生数学抽象思维

在等差数列发展的历史中，数学家在探索真知的过程中发生了许多奇妙的经历，产生了非常多的数学故事。而这些数学故事可以根据具体的教学内容和教学目标进行挑选，选择最为恰当内容，之后使用恰当的方式融入到课堂教学中。在具体的教学过程中，如果我们可以将这些数学故事与具体的教学内容相结合，并以此为基础进行实践教学，便可以使学生通过在数学故事中抽象出数学概念、命题、方法等来培养学生的数学抽象思维。所以，在“等差数列”的教学中，我们完全可以通过利用数学故事创设情境的方法将学生们引入到具体的教学情境当中，培养学生数学抽象素养。

例如，在讲“等差数列的前n项和”时，教师可以利用“高斯求和”的数学故事创设教学情境。具体的教学过程如下：向学生提出这样一个问题：“数学家高斯10岁的时候很快就解决了问题：1+2+3+4+5+…+100=？你知道高斯是怎样算出来的吗？”随后在学生讨论后，向学生展示高斯的求和过程。最后可以布置课外作业，以学习小组的方式请同学们查找高斯的生平事迹以及他在数学中的贡献，在下一次的课堂向班级中其他学生分享。通过此教学情境可以引起学生的疑问，激发学生的学习兴趣，同时使学生结合具体的教学情境感受等差数列求和公式的推导过程，有效培养学生的数学抽象核心素养，达到高效教学的目的。

5.2 借鉴数学家的思想方法进行公式推导，增强学生逻辑推理能力

在等差数列发展的历史中存在数学家们宝贵的思想方法，它们都是智慧的结晶。而这些宝贵的思想方法应该根据教学内容和教学目标进行挑选，选择符合学生身心发展水平的内容，之后使用恰当的方式融入到课堂中。在等差数列通项公式和等差数列前n项和公式的推导过程中，教师可以向学生将数学家们的思想方法与公式的推导过程相结合，通过介绍数学家们关于公式推导的思想方法，使学生掌握逻辑推理的基本形式，学会有逻辑地思考问题。并且在这个过程中积极引导学生深入探究公式的推导过程，使学生充分参与探究活动，实现知识迁移，强化学生的理性思维，培养逻辑推理素养。

例如，在讲解“等差数列前n项和公式”时，可以将阿尔·卡克希撰写的《代数之荣耀》中有关等差數列求和问题的解法渗透到教学过程中。在具体的教学过程中可以向学生介绍阿尔·卡克希撰写的《代数之荣耀》中有关等差数列求和问题的解法。并且在这个过程中教师应引导学生思考解法中蕴含的思想方法，加深对该解法的理解，并借鉴该解法进行公式的推导。通过渗透数学家的思想方法，可以更加真实地体会到倒序相加法求和的思想，培养学生逻辑推理能力。

5.3 参考数学著作设计问题，强化学生数学运算能力

在等差数列的发展历史中存在大量数学著作。这些数学著作种类繁多、内容量大，教师应该广泛收集，选择合适的数学著作，并根据具体的教学内容进行改编。教师可以参考数学著作设计问题，一方面数学问题的解决可以展现出数学的运算性特征，教师通过引导学生解决数学问题来强化学生的数学运算能力;另一方面，利用数学著作设计问题，可以引发学生自主思考与探究。在教学过程中，教师首先引导学生对问题进行分析，找出其中考查的等差数列知识点，然后选择合适的解题思路和解题的方法，最后解决该问题，从根本上强化了学生的数学运算能力。

例如，在学生学习等差数列前n项和公式之后，可以参考《张丘建算经》设计问题。问题如下：今有女不善织，日减功迟。初日织五尺，末日织一尺，今三十日织讫。问织几何？在这个过程中，首先引导学生对问题进行分析，然后进行自主探究，学生能够运用等差数列前n项和公式进行解答，强化数学运算能力。

5.4 依据知识产生的背景设计情境，培养学生数学建模能力

通过等差数列发展的历史，我们了解到等差数列的产生实际上来源于人们的现实生活。所以在教学过程中教师可以结合数学史深入挖掘等差数列产生的实际背景与现实来源，以此加深学生对等差数列的理解和记忆，让学生认识到等差数列来自人们生产和生活的实践，最后作用于实际生活，使等差数列从教材中的理论知识转化成为实际生活中的可操作计算方法，以此来培养学生数学建模的能力。

例如，在讲解“等差数列的概念”时，可以向学生介绍概念产生的背景，设计的教学环节如下：在课前可以给学生布置作业，要求按学习小组查找等差数列产生的背景，在课堂上向班级中其他学生分享。使学生了解到，我国古代的发展主要依靠畜牧业和农业，为了能将生产资料按照等级合理进行分配，“等差”思想应运而生。使学生对等差数列产生了感性的认识。

6 小结

总之，数学科学是最重要的基础科学之一，等差数列是高中数学的重要内容之一。而数学史是一座巨大的宝藏，为教师在课堂上落实数学核心素养提供了丰富的教学素材和思想养料。本文首先分析核心素养下等差数列的具体内容和等差数列中的数学史内容，并在此基础上提出相应的教学措施。但本文的研究有限，对于等差数列中数学史的内容也不够全面，还需要多方面查阅文献，充分挖掘可以与教学内容相结合的数学史内容，实现核心素养下数学史内容融入到等差数列的教学中，作为教育工作者任重而道远。

参考文献：

[1] 朱立明，马云鹏.核心素养视角下数学史教育的价值与策略[J].中小学教材教学，2016（11）：55-58.

[2] 高山.探讨数学史对提高高中学生数学核心素养的价值和策略[J].高中数理化，2021（04）：26-27.

[3] 赵虎.浅谈数学学史对提高高中学生核心素养的价值[J].家长，2021（21）：171-172.

[4] 中华人民共和国教育部.普通高中数学课程标准（2017年版）[M].北京∶人民教育出版社，2018.

作者简介：

魏子薇：（1997.09—），女，汉族，黑龙江省绥化市人，宁夏师范学院硕士在读。研究方向：学科教学（数学）。