基于Lasso-logistic回归和随机森林模型的院校评价结果影响因素研究

何 双，赵国瑞，崔庆岳

(1.阳江职业技术学院数学系，广东 阳江 529566；2.广东海洋大学阳江校区，广东 阳江 529566)

0 引言

我国大力推动本科“双一流”高校与学科、高职“双高”院校与专业建设，分别在2017年、2019年评出第一批“双一流”、“双高”院校.如何厘定各因素指标对评价结果的影响程度，厘清其内部的作用机制，目前是教育技术学、教育评价学等领域，尤其是教育数据挖掘领域(Education Data Mining，EDM)研究的热点问题，其研究价值在于对高校精准施策、实现内涵式建设与发展具有参考意义.

就该领域研究对象与方法来看，崔育宝等[1]就我国在世界一流大学建设评价标准与体系的构建等问题进行了深入的分析；孔晓明等[2]对“双一流”建设评价的原则及方法进行了分析；余波等[3]对“双一流”高校数据跟踪评估平台的构建进行了研究；林春树[4]对“双高”院校绩效评价指标体系的设计进行了系统的分析；陈保荣等[5]对各高职院校排行评价指标体系进行了分析.纵观现有研究文献，从研究对象上来说，“双一流”研究较多，也较为深入，“双高”研究较少；从研究方法上来说，定性研究多，定量研究少，并且从我们前期文献搜索来看，基于机器学习算法研究院校评价结果影响因素厘定方法与路径的文献偏少.

Lasso(least absolute shrinkage and selection operator)作为机器学习近些年发展起来的模型被广泛应用到生物信息学、医学与经济学等领域，较为典型且具有拓展性的文献有：方匡南等[6]将Lasso引入银行个人信用风险评估领域；张兴祥等[7]将Lasso引入国民幸福感指标体系构建领域；孙怡帆等[8]将Lasso引入大学生毕业去向预测领域.但将Lasso应用到教育领域，尤其是EDM领域的文献不多.

本文研究的贡献主要体现在三个方面：第一，在入选“双高”评价指标体系构建上，追本溯源，整理了所有申报的230所院校的申报书，结合已有文献，全面梳理了尽可能纳入模型的客观、可量化指标；第二，已有Lasso应用于实践的文献多数采用单个模型算法筛选与回归，仅有筛选的结果，过程往往忽略，本文将Lasso与随机森林模型结合，共同筛选解释变量，全面展现分析过程，佐证模型选择的合理性；第三，在Lasso变量筛选的基础上，对入选“双高”院校具有显著影响的因素进行了分析，并提供了相关的政策建议.

1 Lasso-logistic模型机理

Lasso作为一种兼具变量选择与参数估计的算法最早由TIBSHIRANI[9]在1996年提出，其机理梗概如下：

给定数据集D=(Xj,yj)，j=1,2,…,n,其中，Xj=(xj1,…,xjm)和yj分别表示为解释变量与被解释变量，

(1)

当样本较少而变量很多时，模型容易产生过拟合，为缓解过拟合的问题，可引入L1范数正则化.

再次，能够多角度的呈现事物。信息技术能轻松实现事物的伸缩、定格、整体和局部等，利于幼儿观察，幼儿观察的越广泛、深刻，在大脑中留下的表象就越丰富、清晰，丰富的表象有助于幼儿想象力的发挥，从而提高幼儿的创造力。

(2)

(2)式中第二项表示对系数的惩罚，λ是控制各变量的压缩程度的调节系数，通过λ的变化调节变量的选择，使不重要的变量系数压缩为0.λ越小，惩罚力度越小，保留下的变量越多；而λ越大，惩罚力度越大，保留下的变量越少.在模型求解方面，2004年EFRON等[10]引入了最小角回归算法，使Lasso模型得以更高效地求解.

对于λ的求解，采用R语言中的lars程序包，结合MallowsCp准则与广义交叉验证得到.从p个自变量中选取s个做回归，

(3)

对Lasso压缩剩余的变量做Logistic回归，假设压缩后的变量个数为m，解释变量yj为二元0-1变量，设

(4)

2 数据描述

本研究数据来源于教育部、财政部2019年中国特色高水平高职学校和专业建设计划(简称“双高计划”)申报材料.共收集230个院校样本，其中，深圳职业技术学院等56所院校被列入高水平高职学校建设单位，北京农业职业学院等141所院校被列入高水平专业群建设单位，33所院校未入选.

考虑到若以是否入选高水平学校和专业群建设单位为研究对象，就会造成样本数据存在过大的非对称性分布问题，即入选数量远远大于未入选数量，因此以是否入选高水平高职建设单位计为被解释变量，0表示“否”，1表示“是”.另外，依据各院校申报书构建二级指标体系，其中，解释变量包括2个一级指标、50个二级指标，具体分级指标体系见表1.为验证模型预测效果，将样本数据集按照8∶2的比例随机切分为训练集和测试集.

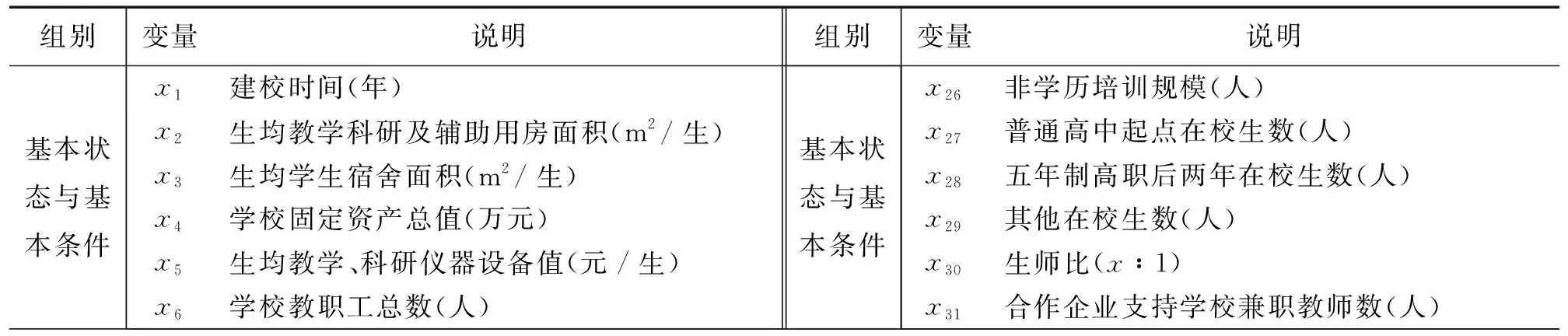
表1 解释变量分级指标体系

续表

3 实证分析

3.1 变量选择与模型估计

采用Lasso-logistic模型分析被解释变量是否入选双高计划(Y)的影响因素，利用R语言中的lars程序包，通过交叉验证法(cross validation，CV)选取调和参数λ，λ在CV下估计值对应趋势见图1，其中使均方误差最小的饱和度在0和0.2之间.由于CV是随机分组，每次分组的不同导致λ结果的不同.而λ的取值不同，Lasso模型压缩程度也将有变化，每次模型选出的变量数目也将受到影响.Tibshirani认为，在模型均方误差较小时，一般选取使模型相对简洁的λ.因此，为保证模型的稳定性，本文重复设定不同随机数，进行10次CV取参数λ的均值，得到λ的均值约为0.101.

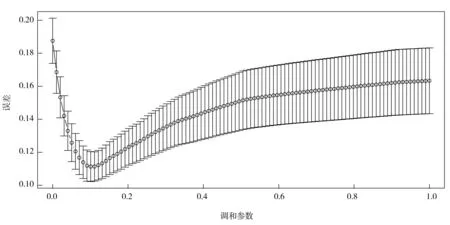
图1 调和参数λ对应趋势图

图2显示了系数随着调和参数λ的选入的路径，对于λ的最小值，只有x37被选入，随着λ的增加，x41、x35等依此被选入模型，当λ接近1时，50个解释变量全都被选入模型.基于CV得到的理想取值λ=0.101，共有x21、x35、x37、x38、x41、x42、x43、x46、x47被选入模型.

图2 Lasso系数的路径

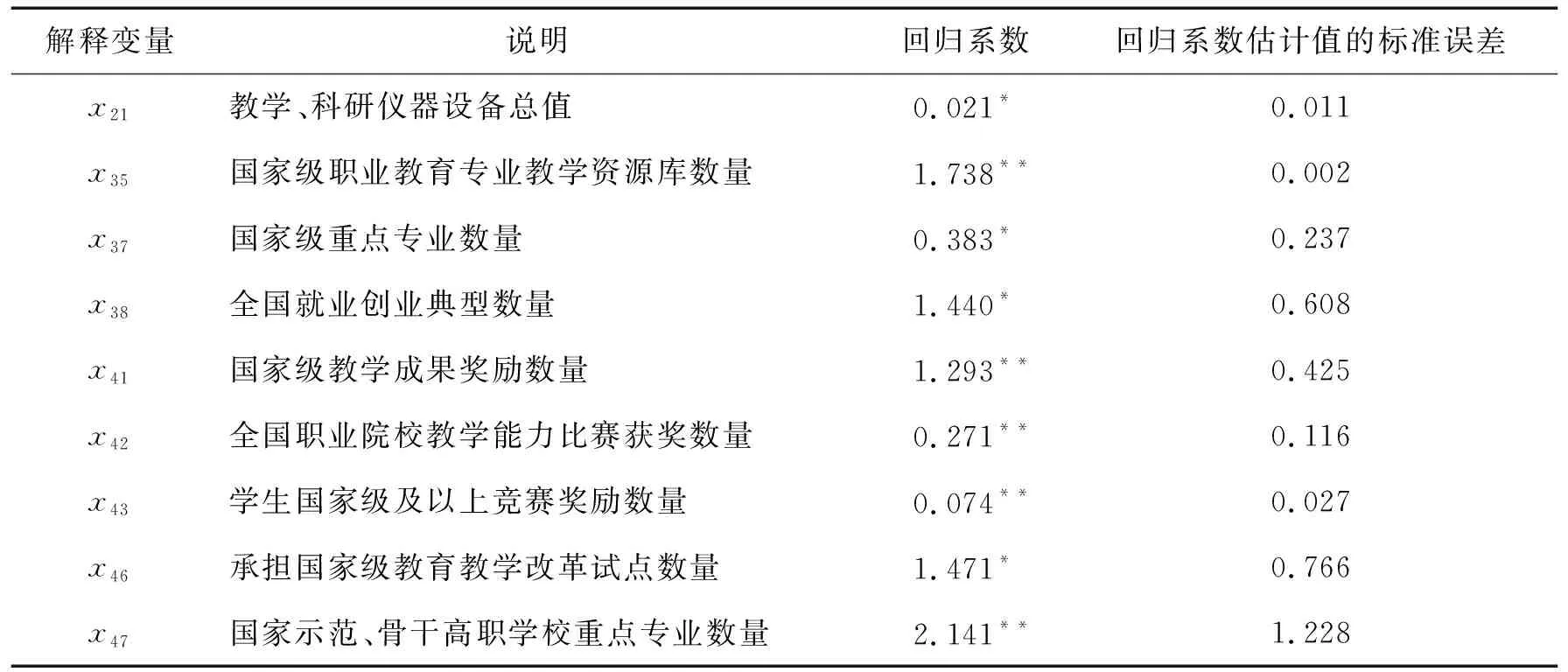
表2 Lasso-logistic模型参数估计

由于数据集本身质量，尤其是解释变量众多，导致Logistic回归及逐步Logistic回归模型复杂度过高，算法不收敛或过拟合情况，因此仅展示Lasso-logistic模型的参数估计结果(表2)，据此可得到回归方程(3)，其中，P为入选双高院校的概率.

1.440x38+1.293x41+0.271x42+0.074x43+1.471x46+2.142x47.

(5)

3.2 各模型准确率的比较

为比较各模型的训练精度，引入支持向量机、决策树、随机森林等模型，分别在训练集和测试集上对入选双高院校和未入选双高院校预测准确率进行对比分析，具体见表3.

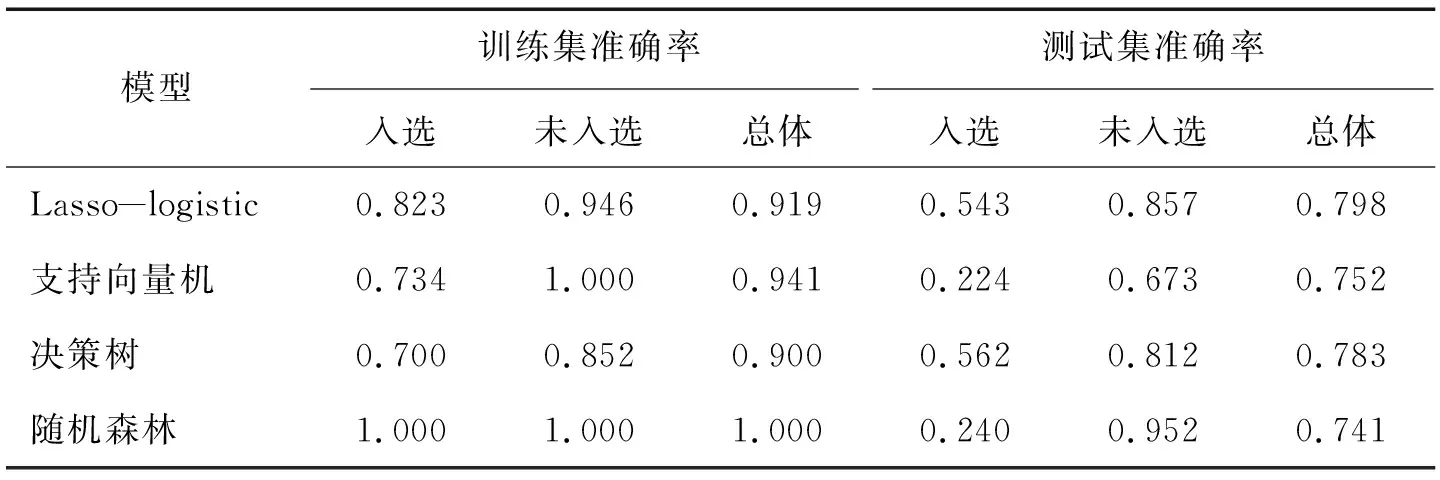
表3 各模型预测准确率比较 单位：%

模型预测的准确率直接关系到模型的合理性，各模型在训练集上的总体准确率均超过90%，但对于入选双高院校而言，Lasso-logistic模型准确率远高于支持向量机和决策树，仅次于随机森林；但在测试集上Lasso-logistic模型总体准确率最高，达到79%，尤其在入选双高院校的准确率上远高于支持向量机和随机森林，仅次于决策树，说明其具有良好的外推性.另外，Lasso-logistic模型压缩了绝大多数变量，较之其它模型复杂度较低，其次，Lasso-logistic模型可解释性更强，可用于是否入选双高院校的影响因素的厘定.

3.3 解释变量重要性的挖掘

为进一步验证各个解释变量相对于被解释变量Y的重要性，引入集成算法中的随机森林模型，采用平均精度下降值(mean decrease accuracy，MDA)，本文记为M，评估各特征对结果准确率的影响，具体计算如下：

任取一个特征或解释变量定义为X，第一，对于随机森林中的所有决策树，采用袋外数据OOB估计袋外数据误差，计作B1；第二，对袋外数据OOB所有样本的特征X随机加噪声干扰，例如改变特征X处的值，再计算其袋外数据误差，计作B2；第三，假定随机森林中有N棵决策树，将特征X的重要性记作M(X)，则

(6)

上述MDA的原理可大致看作：对某一特征随机加入噪声后，若袋外准确率大幅度降低，说明该特征对样本分类结果的影响很大，进而说明其重要程度较高.

根据(6)式可求得50个特征的M值，限于篇幅，仅展示重要性排名前十的特征，见表4.对比表2中Lasso-logistic筛选出的变量，除x38(排名17)、x46(排名16)、x47(排名12)以外,均在随机森林模型变量重要性中排名前十，再次验证了Lasso-logistic筛选变量的高效性与一致性.

表4 各变量平均精度下降值

3.4 结果分析

双高院校评价结果受到了诸多主、客观因素的影响，呈现出多因性，而且维度较高，仍有很多解释变量未纳入指标体系.结合Lasso-logistic和随机森林模型结果(表2)，得到如下结果：

第一，在院校基本状态与基本条件组别共34个解释变量，Lasso仅筛选了教学、科研仪器设备总值x21，且在10%的显著性水平下显著，其对于入选“双高”具有重要作用且统计上显著影响，而该变量表征的是学校办学实力的一个重要体现.

结合随机森林对于变量排序结果，学校固定资产总值x4与在校生数x13对入选“双高”也有重要影响，x4与x21表征的内涵基本一致，这说明学校加大教学、科研设备及固定资产投资是入选“双高”的前置因素；在校生数x13虽未被Lasso选出，但仍对入选“双高”有重要影响，这说明规模效应仍是高职院校发展的主流.入选“双高”对于在校生人数仍有相当的门槛限制，这是有别于本科院校的地方.

在基本状态与基本条件组别，其它解释变量未产生实质性影响.例如，建校时间x1未被选出，原因或许是各高职院校大多是经过转置、合并而来；校内专任教师人数x23、生师比x30未被选出，说明不要单纯追求数量的堆积，更应该加强成果、内涵建设.

第二，在标志性成果组别共16个解释变量，Lasso筛选了国家级教学资源库数量x35、国家级重点专业数量x37、全国就业创业典型数量x38、国家级教学成果奖励数量x41、全国职业院校教学能力比赛获奖数量x42、学生国家级及以上竞赛奖励数量x43、承担国家级教育教学改革试点数量x46、国家示范、骨干高职学校重点专业数量x47等8个变量，其中，x35、x41、x42、x43、x47在5%的显著性水平显著，这意味着它们对入选“双高”具有重要作用，说明国家级专业、教师竞赛、学生竞赛等教学成果是入选“双高”院校的关键影响因素.

4 结论

本文将Lasso-logistic模型引入教育数据挖掘领域的院校评价结果影响因素研究中来，挖掘隐藏在评价结果背后的因素与作用机理，主要研究结论有：第一，从研究问题来看，高职院校不应过分追求学生与教师规模等，国家级别的专业教师竞赛、学生竞赛是入选“双高”院校的核心因素，各学校应夯实基础，做好此类标志性成果的建设与积累；第二，从研究方法来看，Lasso更有效地压缩、筛选关键变量，降低了模型的复杂度，而且总体精度优于其它算法，并且其结果与随机森林模型验证的结果基本一致，因此，采用Lasso厘定院校评价结果的影响因素是较为合理与科学的.第三，从研究局限来看，教育评价影响因素的厘定作为教育数据挖掘领域的一类问题，其背景交叉了教育技术学等学科，诸多因素很难甚至不可能量化到解释变量中来，这也影响了数据集的质量.总之，将机器学习的模型算法，尤其是Lasso等稀疏化算法引入到教育数据挖掘领域，仍不失为有益的尝试.