初中几何证明题复习题型设置初探
2022-03-16福建漳州市第三中学363000张秋菊
福建漳州市第三中学(363000) 张秋菊
传统的初中几何复习课中,教师大多是先让学生回顾梳理已学知识,然后再让学生进行习题练习。这样的复习课不但枯燥乏味,而且学生兴趣不大,教学效率也不高。对此,教师在引导学生复习知识点的同时还应引导学生找到数学本质,总结归纳出解题的一般思路,进而逐步培养学生观察、比较、分析、综合和概括的能力。初中几何证明复习课中,复习题型的设置是关键。下面笔者结合教学实践,介绍三类初中几何证明题的复习题型。
一、“一题多解”题型
在初中几何证明复习中设置“一题多解”题型,不仅能让学生牢固掌握和运用所学知识,还能让学生通过分析比较多种解法,找到解题的最佳途径和方法,培养学生的创造性思维。
[例1]如图1,已知AB=DC,AC=DB,试说明:∠1=∠2。
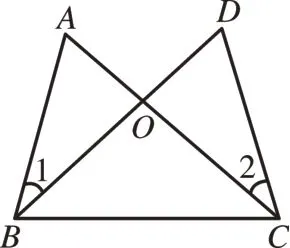
图1


此例可在复习三角形全等时设置。从学生独立完成到教师展示评价,多种解法应运而生,而从这些解法中,学生牢固掌握了三角形全等的判定和性质。通过比较分析,显然解法四是最简单的。
[例2]如图2,在平行四边形ABCD中,BE=DF,求证:四边形AECF是平行四边形。
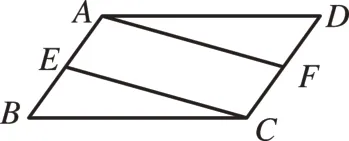
图2


此例可在复习平行四边形的判定时设置。关于平行四边形的证明通常有5 种判定方法:①两组对边分别平行;②两组对边分别相等;③一组对边平行且相等;④两条对角线互相平分;⑤两组对角分别相等。此例用了4 种判定来证明,这大大提高了复习的效率。通过解法优化比较,发现解法一是最简便的。
二、开放性题型
开放性题型可为每个学生提供更多交流与合作的机会,学生通过积极主动的思考和交流,培养了发散性思维,提高了数学学科核心素养。开放性题型在初中几何证明中的优势尤为突出。
[例3]如图3,要使△EDB≌△EAC,△AOB≌△DOC,需添加的两个条件是____________,并说明理由。

图3
分析:因为图中隐含公共角和对顶角,所以不管添加的条件是先使△EDB与△EAC全等,还是先使△AOB与△DOC全等,都是添一角一边或是两边。不过要注意在添两边时必须是夹公共角或对顶角的两边。
此题一出,学生就进行了激烈的讨论,通过讨论发现此题可添的条件不下10 种。例如:①AE=DE,BE=CE;②AE=DE,∠B=∠C;③AC=BD,∠B=∠C;④AE=DE,∠EAC=∠EDB;⑤BE=CE,∠B=∠C;⑥OA=OD,OB=OC;⑦OA=OD,∠B=∠C;⑧OB=OC,∠B=∠C;⑨OB=OC,∠BAC=∠CDB;⑩AB=CD,∠B=∠C;等等。这样,学生根据自己的体验,用自己的思维方式,自主去探索,去发现有关的数学知识,既调动了学生的学习积极性和主动性,又使学生对判定定理印象深刻,大大提高了复习效率。
三、变式题型
在初中几何证明复习课中设置变式题型,可以引导学生多方面、多角度、多途径地思考问题,让学生多合作探讨、多交流争论,从而有效培养学生的创造性思维。
[例4]如图4,已知OA=OD,AC=BD。试说明:∠B=∠C。

图4
分析:由已知OA=OD,AC=BD,根据等式的基本性质得到OB=OC。因为∠AOB与∠DOC是对顶角,所以∠AOB与∠DOC相等,可得△AOB≌△DOC。再由全等三角形的对应角相等得∠B=∠C。

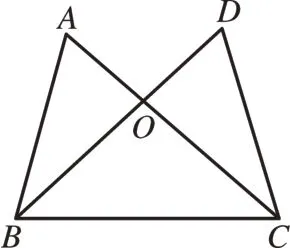
图5

变式2:如图6,BE=CE,AB=DC,请你在图中找出所有全等三角形,并说明理由。

图6

变式3:如图7,EO平分∠BEC,CA⊥BE于点A,BD⊥CE于 点D。求 证:OB=OC。

图7

此例可在专题复习判定三角形全等时设置。此例从原题到变式是由全等基本图形通过添边或角来变化的,学生可以直观感知图形之间的关系,并且对常考的重点模型进行详细分析,加深对全等基本模型的理解,掌握全等三角形的证明方法,培养几何直观能力、推理能力、思维能力和概括归纳能力。
[例5]如图8,在平行四边形ABCD中,对角线AC与BD相交于点O,点E,F分别是OA和OC的中点。求证:四边形BFDE是平行四边形。
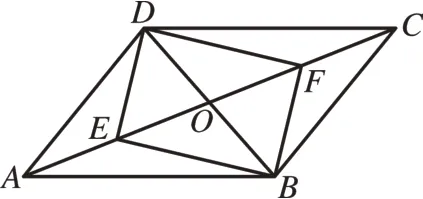
图8
解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵点E,F分别是OA和OC的中点,
∴OE=OA,OF=OC,即OE=OF,
∴四边形BFDE是平行四边形。
变式题:如图9,点E,F是平行四边形ABCD对角线AC上的两个点,且AE=CF。求证:四边形BFDE是平行四边形。

图9
解:连接BD,交AC于点O,
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
又∵AE=CF,∴OA-AE=OC-CF,即OE=OF,
∴四边形BFDE是平行四边形。
变式题与原题相比,部分条件变而需要求证的内容没变,通过这样的变式可帮助学生将所学的知识举一反三、融会贯通。
总之,在几何证明复习课中设置上述题型,既能够激发学生的学习兴趣,调动学生的学习积极性和主动性,促使学生更加扎实地掌握基础知识,提高学生分析问题和解决问题的能力,同时又给学生创造了更多的展示机会,提高了初中几何证明复习的有效性。
