“多题一解”思想在初中数学解题中的应用

陕西理工大学数学与计算机科学学院（723001） 严贵玲

一、初中数学“多题一解”的必要性

“多题一解”是指用同一种数学思想方法解决不同的数学问题，这就要求学生在分析题目时能够由表及里，抓住问题的本质，找出知识的内在联系。学生掌握“多题一解”，能将大量的数学题目化归为一个模块、一个专题，实现做少量的题也能灵活地解决各类难题。

初中阶段正是学生发展数学能力的关键期。随着知识点的增多和学习难度的提高，很多学生的学习水平开始出现明显差异。学好数学的关键点在于能解题、会解题。但是，很多学生都是提笔就写、遇题就做，缺乏对不同题型求解方法的思考和总结，导致学习效果不尽如人意。若能将“多题一解”思想运用到初中数学的学习中，让学生在不同问题情境下对问题进行剖析，并通过对比归纳，形成自己的解题体系，学生就会在面对不同类型的数学题时，能快速反应，选择出合适的解题方法。这样，既能提高学生的解题效率，又能让学生在解题过程中加深对知识内在联系的理解，达到举一反三、触类旁通的效果。

二、“多题一解”思想在特殊三角形存在性问题中的应用

等腰三角形和直角三角形的存在性问题是初中数学的难点问题。解决这两类问题的主要方法是构造“两圆一线”和“两线一圆”模型，在理解题意的基础上，通过绘图辅助，分类讨论出每一种情况的结果。但此类问题的难点在于满足题意的结果不止一种，学生受到定式思维的影响容易遗漏其他的结果。而且计算过程较为复杂，总体来说难度系数偏高。在教学时可将这两大类问题归为两个专题，让学生进行训练，使他们在解题过程中通过类比、迁移、归纳，感悟并掌握“多题一解”思想。

（一）构造“两圆一线”求解等腰三角形存在性问题

［例1］如图1，在平面直角坐标系中，已知点A的坐标为(2,1)，连接OA，若P是x轴上一动点，则当△AOP是等腰三角形时，求点P的坐标。

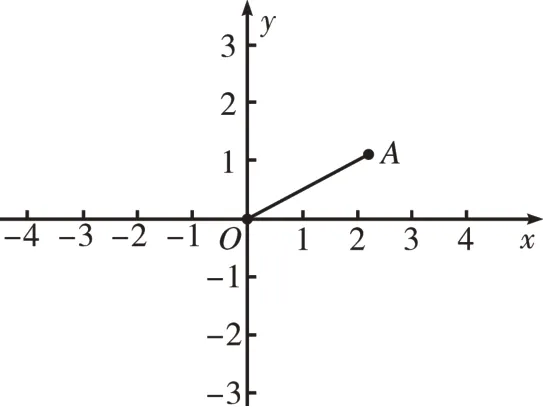
图1

分析：若使△AOP是等腰三角形，那么必有OA=OP或OA=AP或OP=AP。

解：如图2，①当OA=OP时，以 点O为圆心，以OA为半径构造⊙O，此时⊙O与x轴 交 于P1、P2两点，即。

图2

②当OA=AP时，以点A为圆心，以OA为半径构造⊙A，此时⊙A与x轴交于点O（点O不能构成等腰三角形，暂不讨论）和点P3，即P3（4,0）。

③当OP=AP时，作OA的垂直平分线，该直线与x轴交于点P4。此时，设点P4坐标为（x,0），利用勾股定理，可列方程x2=12+(2-x)2，得到

因此，此题共有4 个点能使得△AOP是等腰三角形。

对于这一类题目，通常还会有其他的问法。例如，在同样的条件下，y轴上是否存在点P，使得△AOP是等腰三角形？或者在坐标轴上是否存在点P，使得△AOP是等腰三角形？经过分析，我们发现解题思路和计算过程都可以类比例1。此时y轴上也有4 个点符合题意。同样，当问题是在坐标轴上求点P时，就要综合点P在x轴和y轴上的两种情况，共可求得8个点。

［例2］如图3，在平面直角坐标系中，四边形OABC是长方形，已知A（6,0），C（0,2），M是OA的中点，P是线段BC上的一个动点，当△OMP是腰长为3 的等腰三角形时，求点P的坐标。

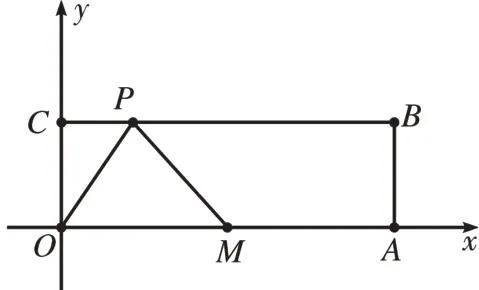
图3

分析：若使△OPM为等腰三角形，可讨论PM=OM、OP=OM和OP=PM这三种情况。

解：如图4所示，

图4

①当PM=OM=3 时，此 时 以 点M为圆心，以OM为半径构造⊙M，其交CB于点P1，P2。分 别 构 造相应的直角三角形，利用勾股定理列出方程，即可求得坐标为

②当OP=OM=3时，以点O为圆心，以OM为半径构造⊙O，其与CB交于点P3，利用勾股定理列出方程，可得

③当OP=PM=3时，作OM的垂直平分线，由图可知，此时△OPM是等边三角形，点P在两圆的交点处，不在CB上，不符合题意，故舍去。

综上所述，共有3个点成立。

［例3］在平面直角坐标系中，点A（2,1），B（0,1），C（-4,-3），D（6,-3），将各点依次连接构成一个四边形ABCD后，求出点P的坐标，使得△APB、△BPC、△CPD、△APD都是等腰三角形。

分析：将各点连接之后，这是一个等腰梯形（如图5），要使得△APB、△BPC、△CPD、△APD这4个三角形都是等腰三角形的点P并不好求。但是仔细分析后可以发现本题的突破点：（1）“△APB、△CPD是等腰三角形”是这4 个等腰三角形成立的先决条件。由于该四边形是等腰梯形，AB和CD有着特殊的位置关系，当△APB和△CPD是等腰三角形时，点P必然在AB、CD的垂直平分线上，即点P在直线x=1 上。（2）该四边形是等腰梯形，则有BC=AD，考虑△BPC和△APD都是等腰三角形的条件时，只考虑点P使△BPC是等腰三角形即可。综上两个关键点，我们可以建立“两圆一线”模型来解决这个问题。

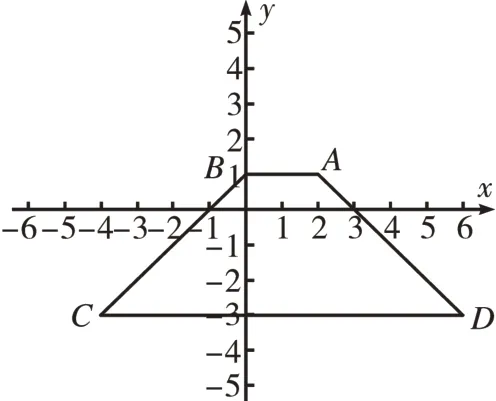
图5

解：对于CB=CP、BC=BP、BP=CP三种情况时，分别构造⊙C、⊙B、BC的垂直平分线（如图6），设点P（1,y）。

图6

综上所述，有5个点符合要求。

求解这一类等腰三角形的存在性问题，只要对问题进行层层分析，将关键点分析到位，就能知道它们属于同一类题，解题方法都是类似的。先根据题意分情况讨论，再构造“两圆一线”模型，最后利用勾股定理和两点间距离公式求解点P。只要熟练掌握这一类解题技巧，那么这类问题也就迎刃而解了。

（二）构造“两线一圆”求解直角三角形存在性问题

［例4］在平面直角坐标系中，点A(1,1)，B(5,3)，在x轴上找一点P使得△ABP是直角三角形，求点P的坐标。

分析：本题中三角形的目标形状是直角三角形，那么必有∠A=90°、∠B=90°、∠P=90°三种情况。

解：如 图7（“两 线 一圆”模型）所示，AB=，设P(x,0)。

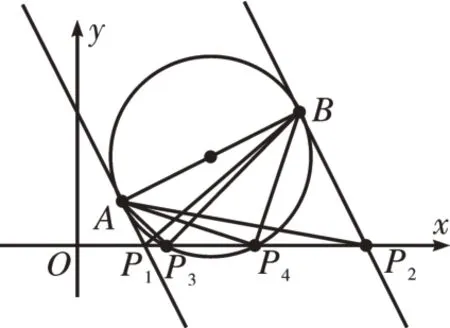
图7

①当∠A=90°时，过点A作AB的垂线交x轴于点P，利用勾股定理AB2+AP2=BP2，列方程为20+(x-1)2+1=( 5-x)2+9，即得。

②当∠B=90°时，过点B作AB的垂线交x轴于点P，此时有AB2+BP2=AP2，列方程为20+(x-5)2+9=(x-1)2+1，即得

③当∠P=90°时，点P在以AB为直径的圆上，此时AB作为斜边，同样利用勾股定理BP2+AP2=AB2，列方程为(x-5)2+9+(x-1)2+1=20，即得P3(2,0),P4(4,0)。综上所述，共有4个点符合要求。

［例5］在平面直角坐标系中，点M(1,4)，A(3,0)，点P是y轴上一点。若使得△PAM是直角三角形，那么有几个满足条件的点P？求出该点坐标。

解：如图8（“两线一圆”模型）所示，AM=，设P(0,y)。

图8

综上所述，共有4个点满足题意。

［例6］在平面直角坐标系中，点A(-2,2)，B（3,2），P是坐标轴上一点，若△ABP是直角三角形。问：满足条件的点共有几个？

分析：本题增加了点P的位置范围，即在坐标轴上。但是方法不变，我们依然可借助“两线一圆”来解决这个问题。本题只用求点P的个数，不要求坐标，降低了解题难度。

解：如图9 所示，构造“两线一圆”模型。

图9

①当∠A=90°时，过点A作AB的垂线与x轴交于点P1；

②当∠B=90°时，过点B作AB的垂线与x轴交于点P2；

③当∠P=90°时，以AB为直径构造圆，其与x轴分别交于点P3，P4，与y轴分别交于点P5，P6。

综上所述，共存在6 个点使得△ABP是直角三角形。

求解直角三角形的存在性问题，学生需要把握题目的本质，精准分析题目。先考虑到有三种直角的情况，再构造“两线一圆”模型，利用勾股定理列出方程即可。只要做到这一步，学生就能通过做一题会一类。通过日常的学习训练，学生求解直角三角形存在性问题的能力就会明显取得进步。

解题能力是数学学习能力的一大组成部分。数学题目种类多、范围广，知识点之间联系紧密。如果学生缺乏“多题一解”思想，很容易被困在题海中，找不到学习数学的有效方法，丧失学习数学的兴趣。本文以解决特殊三角形的存在性问题为例，将不同内容的练习题编织在一起，进行层层分析后，采用同一类方法求解，充分体现了“多题一解”的重要思想。在日常教学中，培养学生的“多题一解”思想，有利于加强学生对知识的熟悉程度，有利于学生对数学思想方法的掌握和运用，达到强化训练的目的，形成解题技巧，提升学生自身的数学素养。因此，“多题一解”在初中数学学习中具有显著作用，应当成为学生学习数学的重要思想。